二叉树简单实现(C语言版)
一.简单建二叉树
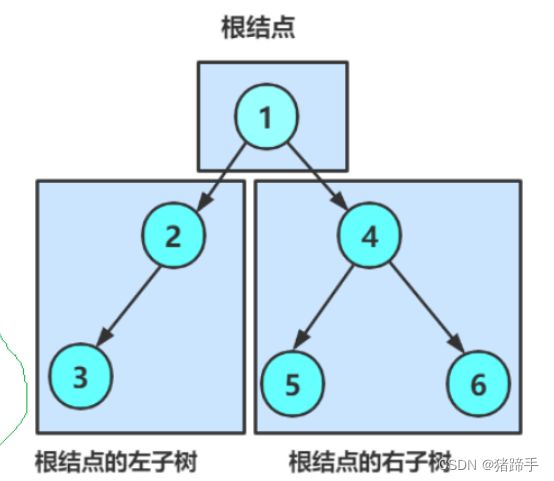
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二 叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树 操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
所以我们先简单建一个二叉树:
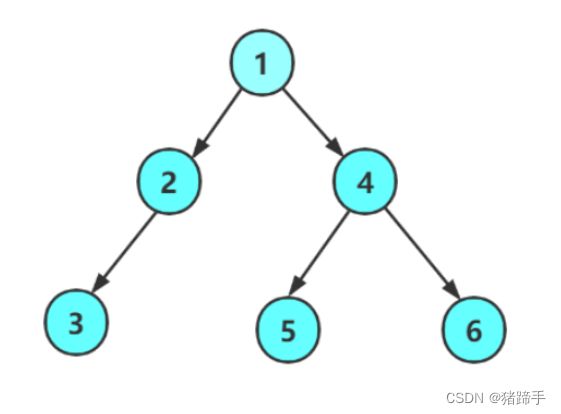
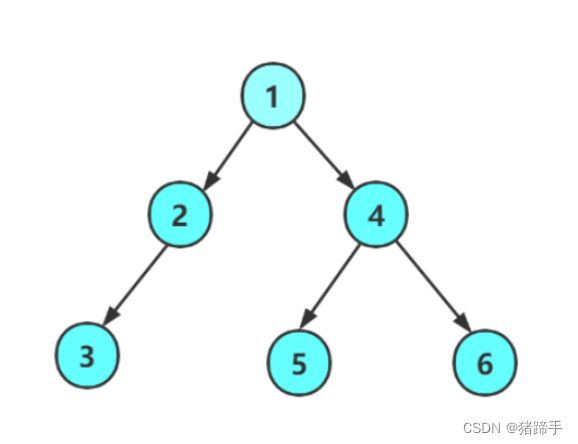
以该二叉树为例:
//法一
TreeNode* Creat()
{
//开辟树的空间
TreeNode* node1 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node1);
TreeNode* node2 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node2);
TreeNode* node3 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node3);
TreeNode* node4 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node4);
TreeNode* node5 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node5);
TreeNode* node6 = (TreeNode*)malloc(sizeof(TreeNode));
assert(node6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
//对每个进行赋值
node1->date = 1;
node2->date = 2;
node3->date = 3;
node4->date = 4;
node5->date = 5;
node6->date = 6;
return node1;
}但是你会发现,这是一个明显可以简化的代码
简化结果如下:
//法二
TreeNode* BuyTreeNode(int x)
{
//开辟树的空间
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->date = x;
node->left = NULL;
node->right = NULL;
return node;
}
TreeNode* Creat()
{
//开辟树并且对每个进行赋值
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
由于学习要逐渐深入,所以我们先简单构建二叉树。
二.二叉树的遍历
二叉树的概念:
二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的
你会发现:
二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
回到我们的主题上:
二叉树主要分为四种遍历:
2.1.前序遍历
定义:
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前
即:先根-》左子树-》右子树
回到我们前面的例题,如果该树是前序遍历,请问结果是什么?
注意:无写成NULL形式
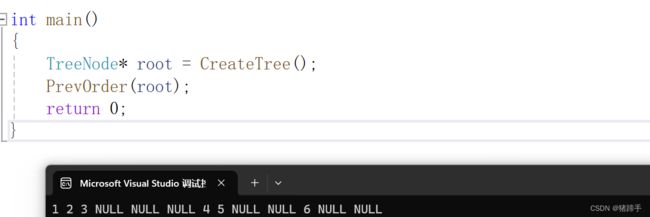
结果为: 1->2->3->NULL->NULL->NULL->4->5->NULL->NULL->6->NULL->NULL
初学时一定不要省略了NULL,这有助于我们理解
下面我们用代码实现前序:
// 二叉树前序遍历
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
else
{
printf("%d ", root->date);
PrevOrder(root->left);
PrevOrder(root->right);
}
}结合前面我们建的二叉树,输出结果:
//法二
TreeNode* BuyTreeNode(int x)
{
//开辟树的空间
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->date = x;
node->left = NULL;
node->right = NULL;
return node;
}
TreeNode* CreateTree()
{
//开辟树并且对每个进行赋值
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
//
// 二叉树前序遍历
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
else
{
printf("%d ", root->date);
PrevOrder(root->left);
PrevOrder(root->right);
}
}
int main()
{
TreeNode* root = CreateTree();
PrevOrder(root);
return 0;
}2.2.中序遍历
定义:
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
即:左子树-》树根-》右子树
同上,回到上面题目:
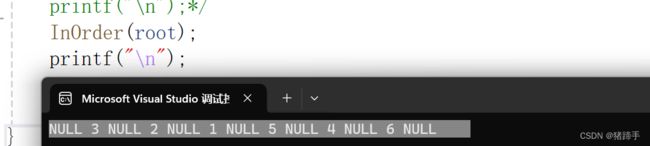
结果:NULL->3->NULL->2->NULL->1->NULL->5->NULL->4->NULL->6->NULL
代码如下:
// 二叉树中序遍历
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
InOrder(root->left);
printf("%d ", root->date);
InOrder(root->right);
}
}还是检验下:
TreeNode* BuyTreeNode(int x)
{
//开辟树的空间
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->date = x;
node->left = NULL;
node->right = NULL;
return node;
}
TreeNode* CreateTree()
{
//开辟树并且对每个进行赋值
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
// 二叉树中序遍历
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
InOrder(root->left);
printf("%d ", root->date);
InOrder(root->right);
}
}
int main()
{
TreeNode* root = CreateTree();
InOrder(root);
printf("\n");
return 0;
}2.3.后序遍历
定义:
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后
即:左子树-》右子树-》树根
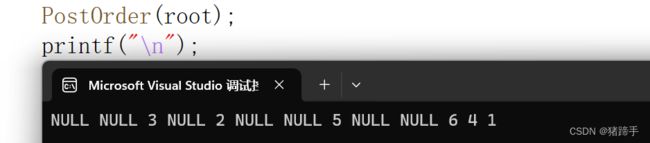
上面的树结果:NULL->NULL->3->NULL->2->NULL->NULL->5->NULL->NULL->6->4->1
代码如下:
// 二叉树后序遍历
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->date);
}
}验证:
TreeNode* BuyTreeNode(int x)
{
//开辟树的空间
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->date = x;
node->left = NULL;
node->right = NULL;
return node;
}
TreeNode* CreateTree()
{
//开辟树并且对每个进行赋值
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
// 二叉树后序遍历
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->date);
}
}
int main()
{
TreeNode* root = CreateTree();
PostOrder(root);
printf("\n");
return 0;
}2.4.层序遍历
层序遍历 :除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1 ,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第 2 层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历
后面我们会讲(下一个文章)
三.实现二叉树接口
3.1二叉树节点个数
还是对于这个二叉树,请用递归实现求它的节点个数
你想到了吗?如果没有,请看看我的实现吧!
对于这棵树,是不是可以看成左子树+右子树+树根,也就是左子树+右子树+1,左子树是不是也可以继续看成左子树+右子树+树根,即左子树+右子树+1,右子树同理,所以我们因此就实现了递归
看代码:
// 二叉树节点个数
int BinaryTreeSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
}有煤油恍然大悟的感觉!
检验:
int main()
{
TreeNode* root = CreateTree();
int ret = BinaryTreeSize(root);
printf("%d\n", ret);
return 0;
}
(我省略了建树的代码,需要可以去前面找,后面我都会适当省略)
结果
3.2.二叉树叶子节点个数
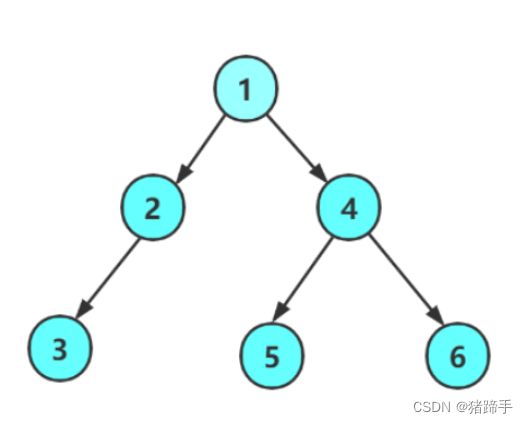
(后面都是这棵树)
对于这个二叉树,请用 递归实现求它的 二叉树叶子节点个数
我这里就直接写了,当然你可以思考之后再看下面的代码。
要解决这个问题,关键是在于要知道什么是叶子节点,是不是它的左右子叶都是NULL,那么递归是不是就好理解了,如果为NULL,0个叶,如果左右子叶都是NULL,它为子叶
看代码:
// 二叉树叶子节点个数
int BinaryTreeLeafSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else if ((root->left == NULL) && (root->right == NULL))
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}验证:
int main()
{
TreeNode* root = CreateTree();
int ret2=BinaryTreeLeafSize(root);
printf("%d\n", ret2);
return 0;
}
3.3.二叉树的高度
也可以认为是深度
还是递归法。
是不是树高度=max(左子树,右子树)+1;左子树高度=max(左子树,右子树),右子树同理。
代码如下:
//法一
//二叉树的高度
int BinaryTreeHeight(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
int left = BinaryTreeHeight(root->left);
int right = BinaryTreeHeight(root->right);
return fmax(left, right) + 1;
}
}//法二
//二叉树的高度
int BinaryTreeHeight(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
return fmax(BinaryTreeHeight(root->left), BinaryTreeHeight(root->right)) + 1;
}
}验证:
int main()
{
TreeNode* root = CreateTree();
int ret3 = BinaryTreeHeight(root);
printf("%d\n", ret3);
return 0;
}3.4.二叉树第k层节点个数
求第K层节点个数,这是不是也是一个递归的题目,当K==1时,是不是就是一个节点,当k>1时,是不是可以依次递减。
代码实现过程:
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(TreeNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
else
{
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
}
检验:
int main()
{
TreeNode* root = CreateTree();
int ret4=BinaryTreeLevelKSize(root, 2);
printf("%d", ret4);
int ret5 = BinaryTreeLevelKSize(root, 3);
printf("%d", ret5);
return 0;
}3.5.二叉树查找值为x的节点
对于查找用递归来写,我们还是可以按照之前的方法,用分治法来解决。
情况一:root==NULL时,是不是该返回NULL
情况二:不为空,root本身为结果
相当于找自身,不行的话就找左子树和右子树
难点是找到之后如何将地址返回到开始的位置
是不是我们可以提前保存一下;找到返回保存值,依次回溯该值即可。
下面我们实现它:
//法一
// 二叉树查找值为x的节点定义
TreeNode* BinaryTreeFind(TreeNode* root, BTDateType x)
{
if (root == NULL)
{
return NULL;
}
if (root->date == x)
{
return root;
}
TreeNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1 != NULL)
{
return ret1;
}
TreeNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2 != NULL)
{
return ret2;
}
return NULL;
}
检查:
int main()
{
TreeNode* root = CreateTree();
PrevOrder(root);
printf("\n");
TreeNode* ps = BinaryTreeFind(root, 4);
if (ps == NULL)
{
printf("没找到\n");
}
else
{
ps->date = 5;
PrevOrder(root);
printf("\n");
}
return 0;
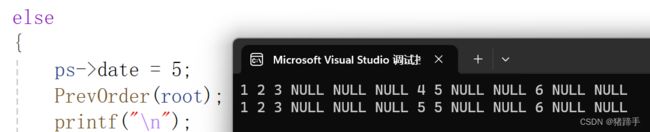
}如果找到的话结果4会变成5,看结果:
没问题,下面我们来用第二种方法实现:
//法二
TreeNode* BinaryTreeFind(TreeNode* root, BTDateType x)
{
if (root == NULL)
{
return NULL;
}
if (root->date == x)
{
return root;
}
TreeNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1 != NULL)
{
return ret1;
}
return BinaryTreeFind(root->right, x);;
}
结果没问题,大家可以深入理解下。
你是否发现这只是前序查找顺序,但是实际中,不一定就是前序查找,你是否会写中序,后序呢?
3.6.通过前序遍历的数组构建二叉树
这个是扩展知识,大家可以了解如何真正建树。
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
TreeNode* BinaryTreeCreate(char* arr, int* pi)//注意:char
{
if (arr[(*pi)] == '#')
{
(*pi)++;
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
//判断开辟情况
if (root == NULL)
{
perror(root);
exit(-1);
}
root->date = arr[(*pi)++];
root->left = BinaryTreeCreate(arr, pi);
root->right = BinaryTreeCreate(arr, pi);
return root;
}3.7.二叉树销毁
任何程序都要在不使用时进行销毁,所以我们下面来实现销毁接口。
// 二叉树销毁(一级指针法)//需要外面手动置空
void BinaryTreeDestory1(TreeNode* root)
{
if (root == NULL)
return;
//后序销毁法
BinaryTreeDestory1(root->left);
BinaryTreeDestory1(root->right);
free(root);
}// 二叉树销毁(二级指针法)//不需要外面手动置空
void BinaryTreeDestory2(TreeNode** root)
{
if (root == NULL)
return;
//后序销毁法
BinaryTreeDestory2((*root)->left);
BinaryTreeDestory2((*root)->right);
free(root);
root = NULL;
}
最后,我们所有汇总一下全部文件:
BinaryTreeNode.h:
#pragma once
#include
#include
#include
#include
//定义结构体
typedef int BTDateType;
typedef struct BinaryTreeNode
{
BTDateType date;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}TreeNode;
//动态开辟空间声明
TreeNode* BuyTreeNode(int x);
//建立二叉树声明
TreeNode* CreateTree();
// 二叉树前序遍历声明
void PrevOrder(TreeNode* root);
// 二叉树中序遍历声明
void InOrder(TreeNode* root);
// 二叉树后序遍历声明
void PostOrder(TreeNode* root);
// 二叉树节点个数声明
int BinaryTreeSize(TreeNode* root);
// 二叉树叶子节点个数声明
int BinaryTreeLeafSize(TreeNode* root);
//二叉树的高度声明
int BinaryTreeHeight(TreeNode* root);
// 二叉树第k层节点个数声明
int BinaryTreeLevelKSize(TreeNode* root, int k);
// 二叉树查找值为x的节点声明(前序)
TreeNode* BinaryTreeFindPreamble(TreeNode* root, BTDateType x);
//二叉树查找值为x的节点声明(中序)
TreeNode* BinaryTreeFindmedium(TreeNode* root, BTDateType x);
//二叉树查找值为x的节点声明(后序)
TreeNode* BinaryTreeFindpostorder(TreeNode* root, BTDateType x); BinaryTreeNode.c:
#include "BinaryTreeNode.h"
//法一
//TreeNode* Creat()
//{
// //开辟树的空间
// TreeNode* node1 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node1);
// TreeNode* node2 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node2);
// TreeNode* node3 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node3);
// TreeNode* node4 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node4);
// TreeNode* node5 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node5);
// TreeNode* node6 = (TreeNode*)malloc(sizeof(TreeNode));
// assert(node6);
//
// //确定指向
// node1->left = node2;
// node1->right = node4;
// node2->left = node3;
// node4->left = node5;
// node4->right = node6;
//
// //对每个进行赋值
// node1->date = 1;
// node2->date = 2;
// node3->date = 3;
// node4->date = 4;
// node5->date = 5;
// node6->date = 6;
//}
//法二
//动态开辟空间定义
TreeNode* BuyTreeNode(int x)
{
//开辟树的空间
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->date = x;
node->left = NULL;
node->right = NULL;
return node;
}
//建立二叉树定义
TreeNode* CreateTree()
{
//开辟树并且对每个进行赋值
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
//确定指向
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
// 二叉树前序遍历定义
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
else
{
printf("%d ", root->date);
PrevOrder(root->left);
PrevOrder(root->right);
}
}
// 二叉树中序遍历定义
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
InOrder(root->left);
printf("%d ", root->date);
InOrder(root->right);
}
}
// 二叉树后序遍历定义
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("NULL ");
}
else
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->date);
}
}
// 层序遍历定义(一:一起遍历)
void LevelOrder(TreeNode* root)
{
;
}
// 二叉树节点个数定义
int BinaryTreeSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
}
// 二叉树叶子节点个数定义
int BinaryTreeLeafSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else if ((root->left == NULL) && (root->right == NULL))
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
法一
二叉树的高度定义
//int BinaryTreeHeight(TreeNode* root)
//{
// if (root == NULL)
// {
// return 0;
// }
// else
// {
// int left = BinaryTreeHeight(root->left);
// int right = BinaryTreeHeight(root->right);
// return fmax(left, right) + 1;
// }
//}
//法二
//二叉树的高度定义
int BinaryTreeHeight(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
return fmax(BinaryTreeHeight(root->left), BinaryTreeHeight(root->right)) + 1;
}
}
// 二叉树第k层节点个数定义
int BinaryTreeLevelKSize(TreeNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
else
{
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
}
//法一
// 二叉树查找值为x的节点定义
//TreeNode* BinaryTreeFind(TreeNode* root, BTDateType x)
//{
// if (root == NULL)
// {
// return NULL;
// }
// if (root->date == x)
// {
// return root;
// }
// TreeNode* ret1 = BinaryTreeFind(root->left, x);
// if (ret1 != NULL)
// {
// return ret1;
// }
// TreeNode* ret2 = BinaryTreeFind(root->right, x);
// if (ret2 != NULL)
// {
// return ret2;
// }
// return NULL;
//}
//法二
TreeNode* BinaryTreeFindPreamble(TreeNode* root, BTDateType x)
{
if (root == NULL)
{
return NULL;
}
if (root->date == x)
{
return root;
}
TreeNode* ret1 = BinaryTreeFindPreamble(root->left, x);
if (ret1 != NULL)
{
return ret1;
}
return BinaryTreeFindPreamble(root->right, x);;
}
//二叉树查找值为x的节点定义(中序)
TreeNode* BinaryTreeFindmedium(TreeNode* root, BTDateType x)
{
if (root == NULL)
{
return NULL;
}
TreeNode* ret1 = BinaryTreeFindmedium(root->left, x);
if (ret1 != NULL)
{
return ret1;
}
if (root->date == x)
{
return root;
}
TreeNode* ret2 = BinaryTreeFindmedium(root->right, x);
if (ret2 != NULL)
{
return ret2;
}
return NULL;
}
//二叉树查找值为x的节点定义(后序)
TreeNode* BinaryTreeFindpostorder(TreeNode* root, BTDateType x)
{
if (root == NULL)
{
return NULL;
}
TreeNode* ret1 = BinaryTreeFindpostorder(root->left, x);
if (ret1 != NULL)
{
return ret1;
}
TreeNode* ret2 = BinaryTreeFindpostorder(root->right, x);
if (ret2 != NULL)
{
return ret2;
}
if (root->date == x)
{
return root;
}
return NULL;
}
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
TreeNode* BinaryTreeCreate(char* arr, int* pi)//注意:char
{
if (arr[(*pi)] == '#')
{
(*pi)++;
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
//判断开辟情况
if (root == NULL)
{
perror(root);
exit(-1);
}
root->date = arr[(*pi)++];
root->left = BinaryTreeCreate(arr, pi);
root->right = BinaryTreeCreate(arr, pi);
return root;
}
// 二叉树销毁(一级指针法)//需要外面手动置空
void BinaryTreeDestory1(TreeNode* root)
{
if (root == NULL)
return;
//后序销毁法
BinaryTreeDestory1(root->left);
BinaryTreeDestory1(root->right);
free(root);
}
// 二叉树销毁(二级指针法)//不需要外面手动置空
void BinaryTreeDestory2(TreeNode** root)
{
if (root == NULL)
return;
//后序销毁法
BinaryTreeDestory2((*root)->left);
BinaryTreeDestory2((*root)->right);
free(root);
root = NULL;
}
三.关于树的基本部分就到这了,感谢大家的支持!!!
祝福大家元旦假期快乐。