数模学习day05-插值算法
插值算法有什么作用呢?
答:数模比赛中,常常需要根据已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求,这就是插值的作用
一维差值问题
插值法
1.概念
插值法指的是根据已知数据点的信息,通过建立适当的插值函数或曲线,估计在未知数据点上的数值。插值是一种逼近技术,用于估计缺失数据或填补数据间的间隔。插值法可以用于处理连续变量的数据,如时间序列分析、地理信息系统等领域。常见的插值方法包括线性插值、拉格朗日插值、牛顿插值、样条插值等。插值法的原理是基于已知数据点之间的连续性假设,通过插值函数或曲线来近似描述未知数据点之间的关系。插值法可以帮助我们填补数据缺失、平滑数据、预测未来数据等。
2.一般定义
3.原理
拉格朗日插值法
两个点
三个点
四个点
通过以上规律可以推出
拉格朗日插值多项式
但是使用拉格朗日插值法还是存在一些问题。
龙格现象
存在的一个最大的问题就是龙格现象
提问:插值多项式次数越高误差越小吗???
见下图
红色的是原式
高次差值会产生龙格现象,即在两端处的波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下,不要轻易使用高次插值。
那这怎么办呢?
分段低次插值
问题一:插值多项式次数高精度未必显著提高
问题二:插值多项式次数越高摄入误差可能显著增大
如何提高插值精度呢?采用分段低次插值是一种办法。
1.分段线性插值
n个点,两个点之间构成差值
2.分段二次插值
牛顿插值法
两种插值法对比
总结来说,拉格朗日插值法和牛顿插值法都是常用的插值方法,它们在实际应用中可根据具体情况选择。拉格朗日插值法适用于数据点较少、精度要求较高的情况;而牛顿插值法适用于数据点较多、计算效率要求较高的情况。
所以一般都使用分段插值法
而且上面讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值,而这种插值多项式却不能全面反映被插值函数的性态。然而在许多实际问题中,不仅要求插值函数与被插值函数在所有节点处有相同的函数值,它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值
对于这些情况,拉格朗日插值和牛顿插值都不能满足。
艾尔米特插值
不但要求在节点上的函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求的插值多项式就是艾尔米特插值多项式
分段三次艾尔米特插值
直接使用Hermite插值得到的多项式次数较高,也存在龙格现象。因此在实际应用之中,往往使用分段三次Hetmite插值多项式(PCHIP)
plot函数
matlab代码
% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); % 在同一个脚本文件里面,要想画多个图,需要给每个图编号,否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')
% plot函数用法:
% plot(x1,y1,x2,y2)
% 线方式: - 实线 :点线 -. 虚点线 - - 波折线
% 点方式: . 圆点 +加号 * 星号 x x形 o 小圆
% 颜色: y黄; r红; g绿; b蓝; w白; k黑; m紫; c青
三次样条插值
matlab代码
说明:
(1)LEGEND(string 1,string 2,string 3)分别将字串符1,字符串2,字符串3 ...标注到图中,每个字符串对应的图标为画图时的图标
(2)Location,用来指定标注显示的位置
% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast') %标注显示在东南方向
% 说明:
% LEGEND(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中,每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置
上述两方法对比
n维数据的插值
% n维数据的插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
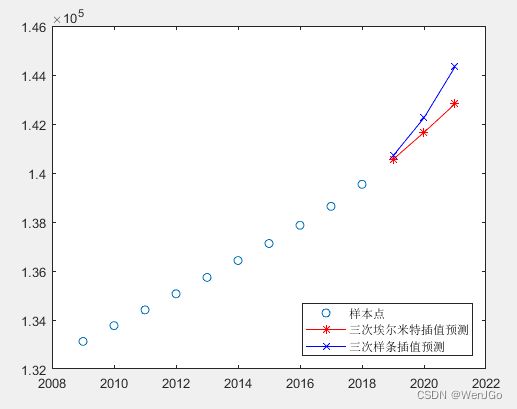
plot(x, y, 'o', new_x, p, 'r-')人口数据预测
% 人口预测(注意:一般我们很少使用插值算法来预测数据,随着课程的深入,后面的章节会有更适合预测的算法供大家选择,例如灰色预测、拟合预测等)
population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
year = 2009:2018;
p1 = pchip(year, population, 2019:2021) %分段三次埃尔米特插值预测
p2 = spline(year, population, 2019:2021) %三次样条插值预测
figure(4);
plot(year, population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')总结
没有