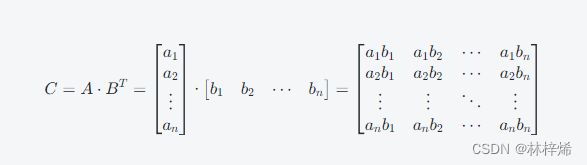机器学习——主成分分析（PCA）
目录
一、特征维度约减
1. 为何要维度约减
2. 特征维度约减的概念
二、主成分分析
1. 主成分
2. 主成分的代数定义
3. 主成分的代数推导
3.1. 第一主成分
3.2. 第二主成分
4. 主成分分析算法流程
三、主成分分析算法实现
四、总结
一、特征维度约减
1. 为何要维度约减
维度约减的目的是为了使高维数据能在二维或者三维的空间可视化，使得我们能够直观的观察数据。维度约减也是为了提高模型算法预测的精度和泛化能力，这是因为大多数的机器学习算法在高维空间中表现不够鲁棒，所谓鲁棒，是指模型在陌生环境或者噪声干扰下依旧能够完成预期任务的能力，维度的增多同时会带来噪声的增多，以及不稳定性的上升，也就导致算法的预测精度下降，维度约减是解决这一问题的有效办法。
此外，多维的特征通常都会包含大量的无用特征，这类特征对结果的价值非常有限，甚至一些特征还会影响预测结果，有价值的特征反而很少。维度约减能够去除这些冗余的特征，降低模型算法的计算开销，同时还能降低噪声，提高算法的稳定性。
2. 特征维度约减的概念
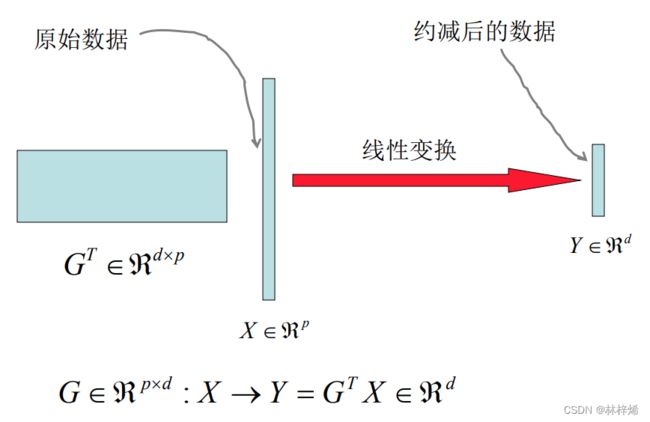
特征维度约减就是将高维的特征向量映射到低维的子空间中，也就是降维操作。
给定n个样本（每个样本维度为p维）
通过特征变换/投影矩阵实现特征空间的压缩：
如下图所示。
特征约减的过程就是找到这样一个变换矩阵，将变换矩阵乘上特征向量就能将特征向量映射到低维的空间中。
二、主成分分析
1. 主成分
特征维度约减的方法有很多种，主成分分析就是其中的一种。
主成分分析的基本思路是：
· 通过协方差分析，建立高维空间到低维空间的线性映射/矩阵
· 保留尽可能多的样本信息
· 压缩后的数据对分类、聚类尽量不产生影响，甚至有所提升
通过投影矩阵就能将原始高维向量投影到低维空间中，数据从原来的坐标系转换到了新的坐标系中。将高维向量进行映射后得到的低维向量被称为主成分，主成分具有无关性、正交的特点，同时主成分的数量远远小于高维空间的维度。
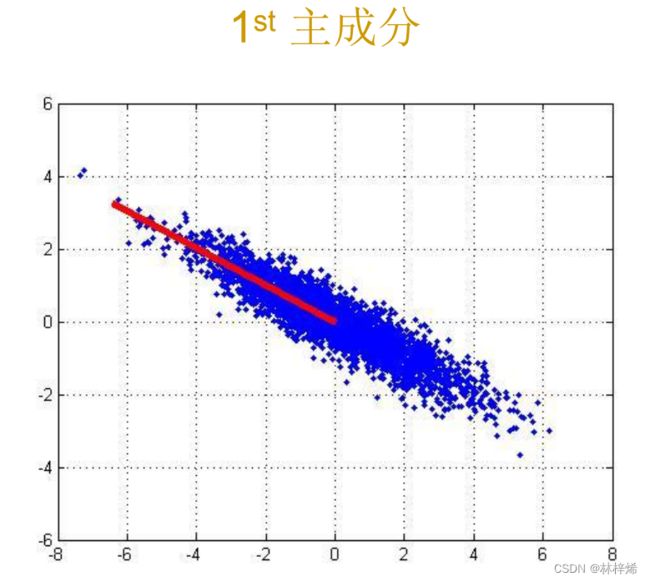
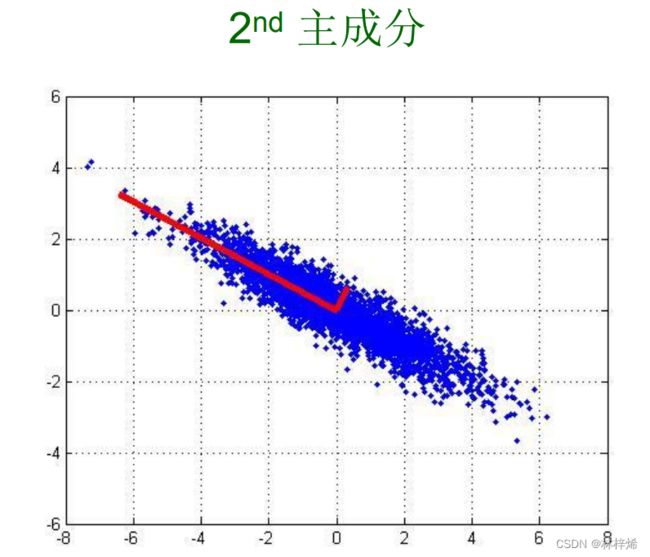
如下图是一个样本数据的两个主成分。
其中第一个主成分是原始数据在所有方向上变化最大的方向，第二个主成分则是在第一个主成分正交的方向上变化最大的方向，如果有更高维的主成分就依此类推。
2. 主成分的代数定义
给定n个样本（每个样本的维度为p维）
定义
为样本
在第一主成分/主方向
上的投影：
其中和都是用向量表示的：
每个样本都对应一个，两个向量进行内积运算就能将映射到方向上，
，如果将的模约束为1，那么和的内积就是
，即样本在主方向上的投影。（为什么是
，如果我没理解错的话，和都是列向量，两个向量的内积应该就是第一个转置成行向量与第二个列向量相乘）
主成分分析的目标是找到，使得
的方差最大，同时要满足约束条件
，对应上面所说第一个主成分是原始数据在所有方向上变化最大的方向，因为变化最大，也就是能够的包含原始数据的变化信息。
3. 主成分的代数推导
3.1. 第一主成分
根据的方差的定义，推导得出：
![var[z_1]=E((z_1-\bar{z_1})^2)=\frac{1}{n}\sum\limits_{i=1}^{n}(a_1^T(x_i-\bar x))^2](http://img.e-com-net.com/image/info8/af3678a28b534226a92dd8a3dd36a1d5.png){kind=small}
其中
是维度之间的协方差矩阵；因为
是p维度列向量，列向量乘以其本身的转置，那得到的结果是p*p的矩阵，每一行的结果是对应行的元素与
对应列的元素的乘积结果，如下图。
中的元素是每个维度的值，这样的乘积结果自然是维度之间的乘积结果。对应
就是维度之间的协方差了。
是样本均值，在实际计算中，可以先将样本均值化，也就是将样本减去均值，使得
，可以简化计算。
这样，协方差矩阵S就可以表示为：
其中![X=[x_1, x_2,...,x_n]](http://img.e-com-net.com/image/info8/c662d016c7ec4224ac11fdd61619f485.png){kind=small}
是由所有样本组成的矩阵，且协方差矩阵S是半正定的。X是行向量，X中的样本是列向量，我感觉这么表示有点怪，这样的矩阵中样本是按列存储的，每一列对应一个样本，而我们一般读取的数据集样本都是按行存储的，一行对应一个样本。
如果X用列向量表示的话，也就是
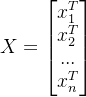
其中
是列向量，那么
就是行向量，表示一个样本，此时协方差矩阵S就可以表示为：
推导公式的时候用的都是向量表示，在算法实现的时候用的是矩阵，运算时谁转置乘法运算的顺序是什么都可能会改变，线性代数没学好看这些就很头晕。
这样问题求解的目标就是找到主成分，使得的方差
最大，同时要满足约束条件
（的模为1），这也是一个带约束的多元函数求极值的问题，因此可以用拉格朗日乘子法来求解。
构造拉格朗日函数：
得到：
在特征值分析中，如果一个特征向量被某个矩阵左乘，那么它就等于某个标量乘以特征向量，例如
中，A是一个矩阵，v是特征向量，那么就能得到
，其中
是特征值，它是一个简单的标量值。
因此从上式可以得出是协方差矩阵S的特征值，是S的特征向量。
再把代回原式（的方差），可以得到：
![var[z_1]=\lambda a_1^Ta_1=\lambda](http://img.e-com-net.com/image/info8/e8d4e27592af46b5a08ec6d834f547c1.png){kind=small}
我们的要求是最大方差，而方差又等于特征向量对应的特征值，那么说明是协方差S的最大特征值，也就是S的最大特征值对应的特征向量，也就是最大特征向量。
3.2. 第二主成分
第二个主成分是在第一个主成分的基础上计算的，第二主成分是在第一个主成分正交方向上，第一主成分和第二主成分是不相关，因此二者的协方差为0，则可以得到：
![cov[z_2,z_1]=0](http://img.e-com-net.com/image/info8/664702660a674caba2025663d8836ca9.png){kind=small}
与第一主成分一样，第二主成分同样模为1，即：
根据协方差的定义，有：
![cov[z_2,z_1]=\frac{1}{n}\sum\limits_{i=1}^n(a_1^T(x_i-\bar x))(a_2^T(x_i-\bar x))^T](http://img.e-com-net.com/image/info8/ff9c5708a9c74b34bb0840b80d430688.png){kind=small}
由前面推导得到的结果，则![cov[z_2,z_1]=a_1^TSa_2=\lambda_1a_1^Ta_2=0](http://img.e-com-net.com/image/info8/8c9cd7cb5b2d49c5908230bf2deef35c.png){kind=small}
第二主成分的计算目标和第一主成分一样，是方差最大，第二主成分的方差为![var[z_2]=a_2^TSa_2](http://img.e-com-net.com/image/info8/c96c26146d9e4cc38b506ba225130efb.png){kind=small}
，同时有两个约束条件，和
，构造拉格朗日函数：
令L对和
的偏导分别为零：
这个我不知道怎么证明出
，也就是也是协方差矩阵的特征向量，可能是
移到右边，然后两边右乘，然后右边就等于0了，但是我不太确定是不是这样，网上也没搜到第二主成分的推导，但反正这个是可以证明出是协方差矩阵S的特征向量，而且是S的第二大特征向量。
依次类推，后面的主成分也可以推导出S的第k大特征向量对应数据的第k主成分。
综上所述，我们只需要将所有特征值排序，然后选择前N个最大的特征值对应的特征向量，这些特征就是最重要的N个特征，再将数据乘上这N个特征向量就能将数据转换到新的空间，也就是完成了特征维度约减的目标。
4. 主成分分析算法流程
主成分分析算法的主要流程为：
计算数据集{x_i}的均值
，并组成变换矩阵
![G\leftarrow[a_1,a_2,...,a_d]](http://img.e-com-net.com/image/info8/9f1cb1018dd34ed0b7d93347a98cd7e2.png){kind=small}
在实际计算中，计算得到数据集{x_i}的均值
后可以将原始数据先去均值，这样就等于0了，可以简化计算。
上述算法主要问题在于如何计算得到S的特征向量，特征值和特征向量的计算过程是：
将关系式
改写为
，这样就能得到一个n个未知数，n个方程的齐次线性方程组，它有非零解的充分必要条件是系数行列式
，即
求解这个方程能得到的n个解，也就是A的n个特征值，将这n个特征值代回进行求解特征向量x就能得到A的n个特征值对应的特征向量。
这个计算的步骤的实现比较麻烦，好在使用numpy库中的linalg模块，该模块的eig()方法可以求解特征值和特征向量，如果用的是torch.tensor存储数据的话可以用torch库中的linalg模块的eig()方法计算，我用的就是这个。
三、主成分分析算法实现
现在编写代码对人脸识别数据集进行降维操作。
使用的数据集为ORL_Faces，样本为图像，数据集包含40个人，每个人10张图片。
读取数据集：
# 读取ORL数据集的函数，testRatio：测试集比例
def loadORL(path, testRatio):
folders = os.listdir(path)
# 一共400个图片
fileNums = 400
# 训练集的样本数量等于总样本数乘1-testRatio，每个样本都是一维数组，大小为112*92
# torch和numpy创建时都要求固定大小，且每一行的长度是相等的，必须保证每个图像的尺寸一样
trainSet = torch.zeros((int(fileNums * (1 - testRatio)), 112 * 92))
trainLabel = torch.zeros((int(fileNums * (1 - testRatio)), 1))
testSet = torch.zeros((int(fileNums * testRatio), 112 * 92))
testLabel = torch.zeros((int(fileNums * testRatio), 1))
# i = 0 ;
l = 0 ; m = 0
# 读取目录下的所有目录
for i, folder in enumerate(folders):
# 获取目录名（目录路径）
folderName = os.path.join(path, folder)
# 只对目录进行处理
if os.path.isdir(folderName):
for j, file in enumerate(os.listdir(folderName)):
fileName = os.path.join(folderName, file)
img = cv2.imread(fileName, 0)
img = torch.from_numpy(img).reshape(1, -1).float()
# 每个目录下面有10个图像文件，其中抽取10 * testRatio个作为测试集
if j < 10 * testRatio:
testSet[l] = img
# 标签用数字表示（从1开始）
testLabel[l] = i + 1
l += 1
else:
trainSet[m] = img
trainLabel[m] = i + 1
m += 1
return trainSet, trainLabel, testSet, testLabel我这里都是用torch张量存储的， 张量定义的时候必须指定大小，而且这个大小是固定的，不能更改（元素个数不能改，形状可以改），所有需要先实现知道每个图像的大小，由于tensor每一行的大小也都是固定的，每个图像的大小（展平成一维后的特征数量）必须相同，不然要进行处理，将每张图片resize成相同尺寸，ORL_Faces数据集每张图片的尺寸好像是相同的，这个格式的文件我不知道用什么打开，反正我运行的时候直接赋值没有resize是没有报错的。
运行：
print(trainSet)
print(testSet)
print(trainSet.shape)
print(testSet.shape)运行结果：
图像数据读取出来应该是二维矩阵（灰度模式读取是二维，彩色图像会多一个通道的维度）， 这里不保留空间信息，只保留数值信息，因此将二维数据展平成一维了，每个样本的维度大小为10304，这是一个非常大的维度。总共有400个样本，其中训练集280个，测试集120个。
PCA算法：
def PCA(dataSet, N):
# 求数据集特征向量的平均值
featMean = dataSet.mean(dim=0).reshape(1, -1)
# dataSetMean的轴1大小和dataSet相同，轴0为1，相减时会进行广播
mcDataSet = dataSet - featMean
# 计算协方差矩阵，数据集均值化后协方差矩阵就等于数据集特征向量乘以自身
# 这里特征向量是用矩阵存储，x^T*X（两个列向量相乘，第一个列向量要转置），需要改为X*X^T
S = mcDataSet.T @ mcDataSet # @是矩阵乘法运算，也可以用torch.matmul()方法
# 使用GPU计算
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
S = S.to(device)
# 计算S的特征值和特征向量
eigVals, eigVec = torch.linalg.eig(S)
# 取前N个特征向量
sortInd = np.argsort(eigVals.cpu()).flip(dims=[0])
vectors_N = eigVec[:, sortInd[: N]]
# 将输入数据降维
lowDDataSet = mcDataSet.to(torch.complex64).to(device) @ vectors_N
return lowDDataSet.cpu(), featMean, vectors_N.cpu()这里数据集样本是按行存储的，每一个是一个样本，所有计算协方差矩阵的时候，先计算数据集特征的平均值，也就是列上（轴0）的平均值，然后将数据集特征值减去平均值，计算时tensor会触发广播机制，不用额外操作，然后再根据公式计算协方差矩阵S，接着调用torch.linalg.eig函数计算S的特征值和特征向量，然后再取出最大的N个特征向量，将原始数据乘上这N个向量就能得到映射后的数据了。
这个要运行非常久，因为协方差矩阵的大小是10304*10304，是10304阶的方阵，计算特征值的时候要先计算10304阶行列式，得到的特征值有10304个，对这10304个特征值分别计算对应的特征向量，特征分解总体的计算量非常大。如果用CPU计算的话计算了七八分钟都没计算出来，后面我换成GPU计算，计算了大概两分钟才出结果。
用tensor做这个有点麻烦，因为特征分解可能会出现虚数，得到的特征值和特征向量都是复数形式的，tensor貌似不太支持复数操作，torch.argsort函数都不支持对复数排序，不过可以用nunpy的argsort函数，这个函数可以正确排序复数，而且tensor数据也支持。但是numpy不能用gpu计算，用numpy.linalg.eig要计算非常久，用pytorch的话可以使用GPU计算，计算时间短很多。
降维后我们要查看数据变化了多少，可以将映射后的数据再映射回原始空间然后再使用pyplot的imshow函数显示图片。
def compare_images(original, reconstructed, index, title1 = 'Original Image', title2 = 'Reconstructed Image'):
original_image = original[index].reshape(112,92)
reconstructed_image = reconstructed[index].reshape(112,92)
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plt.imshow(original_image,cmap='gray')
plt.title(title1)
plt.subplot(1,2,2)
plt.imshow( reconstructed_image,cmap='gray')
plt.title(title2)
plt.show()
此外，我们可以调用分类算法对降维后的数据进行分类，查看分类的准确率。这里我使用最简单的knn算法来分类。
def knnclassfier2(trainSet, trainLabel, testSet, testLabel, k):
true_num = 0
for i, testSample in enumerate(testSet):
# 测试样本和所有训练集（PCA降维后的数据）的距离计算
diffMat = (trainSet - testSample) ** 2
distance = diffMat.sum(dim=1)
sortIndexs = np.argsort(distance)
kCount = torch.zeros(len(set(testLabel)))
for j in range(k):
kCount[int(trainLabel[sortIndexs[j]])] += 1
# y_hat = trainLabel[sortIndexs[0]]
y_hat = np.argmax(kCount)
if y_hat == testLabel[i]:
true_num += 1
return true_num / testSet.shape[0]测试：
这里我先用训练集训练出特征均值和协方差矩阵特征向量，将测试集减去均值再乘上特征向量就能得到降维后的数据，再将降维后的数据乘上特征向量的转置就能映射回原始空间，方便显示图像。最后再调用knn算法计算准确率。
trainSet, trainLabel, testSet, testLabel = loadORL('Face_Dataset/Face/ORL_Faces/', 0.3)
trainLowD, featMean, vector_N = PCA(trainSet, 100)
testSetLowD = (testSet - featMean).to(torch.complex64) @ vector_N
testRecon = (testSetLowD @ vector_N.T)
compare_images(testSet.float(), testRecon.float(), 10)
accuracy = knnclassfier2(trainLowD, trainLabel, testSetLowD, testLabel, 1)
print(accuracy * 100, '%', sep='')测试结果：
将特征降到100维后信息丢失了很多，但还是能看到比较清晰的轮廓的，脸部重要的特征也保留了下来。在k取1的时候准确率是97.5%，这个值有点太高了，我有试了下k取3，准确率降到了90%，这个值正常一点。后面我直接用原始数据分类，得到的结果跟PCA降维到100后的结果一样，这个数据集用PCA降维后看不出来准确率是否有提升，但是计算的复杂度确实是降低了，前提是不算PCA降维的计算复杂度，PCA降维计算的复杂度有点太高了。
下面选择3个N值来分别测试各个N的取值所得到的结果
def ORLFaceRec():
trainSet, trainLabel, testSet, testLabel = loadORL('Face_Dataset/Face/ORL_Faces/', 0.3)
for N in (10, 40, 100):
trainLowD, featMean, vector_N = PCA(trainSet, N)
testSetLowD = (testSet - featMean).to(torch.complex64) @ vector_N
compare_images(testSet.float(), (testSetLowD @ vector_N.T).float(), 0)
accuracy = knnclassfier2(trainLowD, trainLabel, testSetLowD, testLabel, 1)
print('N取', N, '时，准确率为：', accuracy * 100, '%', sep='')测试：
ORLFaceRec()测试结果：
可以看到，N取10的时候，数据信息丢失了非常多，仅凭肉眼是很难分辨出这个人了，预测的结果也差了一些，因为原始数据的特征是10304维，降到10维的话太低了，大量的信息都丢失了。在N取40，100的时候能看出个大概，一些关键的信息还是有保留的，准确率也很高，当然这是k取1的情况，k取2或者更大的时候会降低许多。
四、总结
机器学习算法有监督方法、无监督方法、半监督方法三种，监督方法有标签的训练学习算法，无监督方法是无标签的学习算法，半监督方法是一部分数据有标签，一部分数据没标签的学习算法。PCA算法是无监督方法的一种，主要是对数据集进行降维操作，而不需要对数据集进行分类，因此是不需要标签的机器学习算法。
PCA算法的基本步骤就是将数据集映射到多个主成分上，主成分通过计算推导可以得知是数据集特征之间的协方差矩阵的特征向量，数据集有多少个样本就有多少个特征向量，可以通过计算协方差矩阵的特征值得到对应的特征向量，在实现的时候可以用torch.linalg.eig函数计算协方差矩阵的特征向量，然后从这抽取最大的N个特征向量作为主成分，由这些主成分构成变换矩阵，将原始数据乘上变换矩阵得到映射后的矩阵。
PCA算法将数据降维后可以再使用其他的分类算法对数据集进行分类，一般用简单的线性模型就可以了，这个有点像深度学习，PCA类似深度学习里面的特征提取，用其他分类算法分类类似全连接层预测输出，不过深度学习是依赖梯度下降更新参数得到模型的，不像PCA是直接根据算法来提取特征的。