Day20 222完全二叉树的节点个数 110平衡二叉树 257二叉树的所有路径
222 完全二叉树的结点个数
本题先不把它当成完全二叉树来看,用广度优先和深度优先搜索分别遍历,也能达到目的,只要将之前的代码稍加修改即可。注意后序遍历时的result要加上自身本身的那个结点。
//后序递归遍历
class Solution {
public:
int countNodes(TreeNode* root) {
if(root==nullptr) return 0;
int leftnum = countNodes(root->left);
int rightnum = countNodes(root->right);
int result = leftnum + rightnum +1;
return result;
}
};
//层序遍历
class Solution {
public:
int countNodes(TreeNode* root) {
queue que;
int result = 0;
if(root != NULL)
que.push(root);
while(!que.empty())
{
int size = que.size();
while(size--)
{
TreeNode* node = que.front();
que.pop();
result++;
if(node->left)
que.push(node->left);
if(node->right)
que.push(node->right);
}
}
return result;
}
}; 既然本题给出了条件完全二叉树,那就可以用完全二叉树的方法来做。可以继续使用递归法,终止条件要稍微变一下,要根据左右深度是否相同来判断子树是不是满二叉树,如果是的话就返回2的n次方-1,不是的话就继续递归。为什么左右深度相等就一定是满二叉树呢,这取决于完全二叉树的特性,也就是最后那层肯定是连续的,不存在中间为空的情况。
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};110 平衡二叉树
递归:
要求高度,首先想到要后序遍历,终止条件为遍历到空节点,单层递归逻辑为:分别求出本节点左右子树的高度,如果高度等于-1,就说明左右子树之一不平衡,如果均不为-1, 就继续往下进行,比较左右子树的高度差,大于1说明有问题,返回-1,其余情况正常算高度。
class Solution {
public:
int getHeight(TreeNode* node){
if(node == nullptr) return 0; //终止条件
int leftHeight = getHeight(node->left);
if(leftHeight==-1) return -1;
int rightHeight = getHeight(node->right);
if(rightHeight == -1) return -1;
return (abs(leftHeight-rightHeight) > 1 ? -1 : (1+max(leftHeight,rightHeight)));}
bool isBalanced(TreeNode* root) {
return (getHeight(root)==-1 ? false : true);
}
};
迭代:
本题也可以通过迭代法来进行遍历,但是不能直接用层序遍历来求高度,这就体现出求高度和求深度的不同之处。本题的迭代方式可以先定义一个函数专门求高度。
class Solution {
public:
int getDepth(TreeNode*node)
{
queue que;
if(node!=nullptr) que.push(node);
int depth = 0;
while(!que.empty())
{
int size = que.size();
depth++;
while(size--)
{
TreeNode* cur = que.front();
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return depth;
}
bool isBalanced(TreeNode* root) {
queue que;
if(root == nullptr) return true;
else que.push(root);
while(!que.empty())
{
int size = que.size();
while(size--)
{
TreeNode*node=que.front();
que.pop();
if(abs(getDepth(node->left)-getDepth(node->right))>1)
return false;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return true;
}
}; 257 二叉树的所有路径
本题很明显要进行前序遍历,才方便让父亲节点指向孩子节点,找到对应的路径。但是既然要输出所有的路径,我觉得本题是时候该考虑回溯了。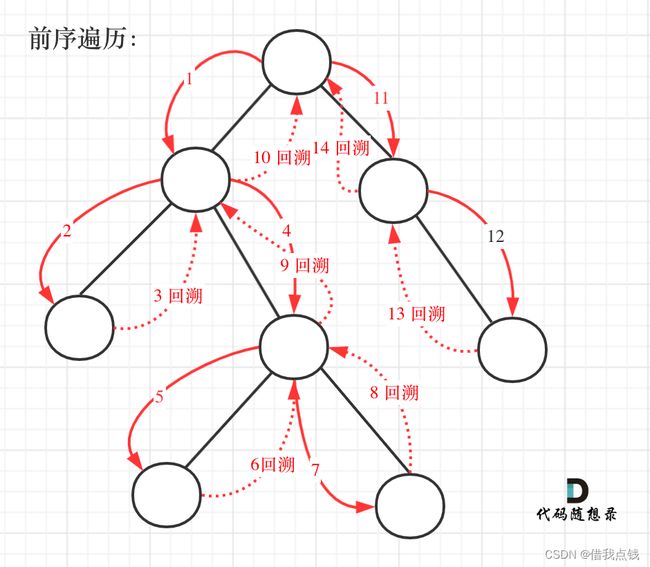
首先是递归法:1.参数返回值:传入根节点,记录每一条路径的path,存放结果的result。
2.递归终止条件。在写递归时都习惯了写cur==null终止,但是本题如果这么写会比较麻烦,因为本题是要找到叶子节点,就结束把路径放进result里的处理了。那么为什么要用vector
要注意:回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!有一个递归,就要对应一个回溯!
整体代码如下:
class Solution {
private:
void traversal(TreeNode* cur, vector& path, vector& result) {
path.push_back(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中
// 这才到了叶子节点
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) { // 左
traversal(cur->left, path, result);
path.pop_back(); // 回溯
}
if (cur->right) { // 右
traversal(cur->right, path, result);
path.pop_back(); // 回溯
}
}
public:
vector binaryTreePaths(TreeNode* root) {
vector result;
vector path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
}; 每次回溯都要pop出此时容器里存放的那个数字,这样就能找出不同的路径了。为什么要用引用呢因为既然每次都pop了,所以说这个path每次都是在变的。
可以精简成如下代码:
class Solution {
private:
void traversal(TreeNode* cur, string path, vector& result) {
path += to_string(cur->val); // 中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // 左
if (cur->right) traversal(cur->right, path + "->", result); // 右
}
public:
vector binaryTreePaths(TreeNode* root) {
vector result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
}; 这个代码里也有递归回溯,因为传入的这个string并不是引用形式,每次执行完毕以后,返回到上一个都不会让这次的影响对上一次进行改变,所以-》要写在递归函数里面,如果写成:
path += "->";
traversal(cur->left, path, result); // 左path就会被改变以后再进行递归,无法进行回溯,这回导致-》重复。如果非要这么写,就得用第一种方法把他pop出去:
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}本题也可以采用非递归的方式,类似于前序遍历的迭代法,不过要定义两个栈,一个是正常迭代法里的那个遍历栈,另一个是保存每次路径的栈:
class Solution {
public:
vector binaryTreePaths(TreeNode* root) {
stack treeSt;// 保存树的遍历节点
stack pathSt; // 保存遍历路径的节点
vector result; // 保存最终路径集合
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
string path = pathSt.top();pathSt.pop(); // 取出该节点对应的路径
if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
result.push_back(path);
}
if (node->right) { // 右
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // 左
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
}; 这两个栈是紧密联系的,上面动的时候,下面也会跟着动。这里的treeSt肯定是只遍历一遍的,但是pathSt里面存的是一个路径,上次遍历的部分会依旧保留,记录了之前遍历过的部分。