bagging:随机森林
前言
集成学习(Ensemble learning)是机器学习中最先进、最有效、最具研究价值的领域之一,这类方法会训练多个弱评估器(base estimators),并将它们输出的结果以某种方式结合起来解决一个问题。
目前来看,集成学习是:
- 当代工业应用中,唯一能与深度学习算法分庭抗礼的算法;
- 数据竞赛高分榜统治者,KDDcup、Kaggle、天池、DC冠军队御用算法;
- 在搜索、推荐、广告等众多领域,事实上的工业标准和基准模型;
- 任何机器学习/深度学习工作者都必须掌握其原理、熟读其思想的领域。
在Bagging集成当中,我们并行建立多个弱评估器(弱评估器是指具有相对较低性能的模型或算法。它通常是一个相对简单的模型,无法独立解决复杂的问题。通常是决策树,也可以是其他非线性算法,很少会去使用线性算法:SVM,岭回归),并综合多个弱评估器的结果进行输出。当集成算法目标是回归任务时,集成算法的输出结果是弱评估器输出的结果的平均值,当集成算法的目标是分类任务时,集成算法的输出结果是弱评估器输出的结果少数服从多数。
Decision Tree:集成学习的背景算法
1、决策树的算法原理
决策树是一种很简单的算法,它的解释性强,是一种基于if-then-else规则的有监督学习算法。对于二分类算法而言,一般会用带正则化项的逻辑回归模型挖掘出的多个分类规则,并且这些分类规则呈现递进的关系,也就是一个分类规则是在另一个分类规则的分类结果下继续进行分类,最终这些分类规则和对应划分出来的数据集呈现出树状,而带有不同层次分类规则的模型。换而言之,决策树模型的构建从本质上来看就是在挖掘有效的分类规则,然后以树的形式来进行呈现。
2、确定数据集划分特征
Q:如果是四分类问题,1条件能够100%区分A类和BCD类,2条件能够100%区分AB类和CD类,此时如何还按照准确率来进行判别分类条件好坏的判别依据,则选择哪个条件就成了问题?
用于衡量数据集标签纯度的数值指标一般有三种,分别是分类误差、信息熵和基尼系数。
(1)分类误差(贪心算法所使用的决策树):
C l a s s i f i c a t i o n e r r o r ( t ) = 1 − max 1 ≤ i ≤ n [ p ( i ∣ t ) ] Classification\ error(t) = 1-\max_{1\leq i\leq n}[p(i|t)] Classification error(t)=1−1≤i≤nmax[p(i∣t)]
i表示第i类,当前数据集总共有n类,p(i|t)代表第i类数据占当前数据集中总数据的比例。而所谓的分类误差,其实就是用1减去多数类的占比。例如某个包含10条数据的数据集,有6条0类数据、4条1类数据,此时该数据集分类误差就是1-6/10 = 0.4。分类误差在[0, 0.5]范围内取值,分类误差越小,说明数据集标签纯度越高。
(2)信息熵(Entropy):
E n t r o p y ( t ) = − ∑ i = 1 n p ( i ∣ t ) l o g 2 p ( i ∣ t ) Entropy(t) = -\sum_{i=1}^n p(i|t)log_2p(i|t) Entropy(t)=−i=1∑np(i∣t)log2p(i∣t)
二元信息熵也是在[0,1]之间取值,并且信息熵越小则说明数据集纯度越高。
信息熵的来源:
信息熵首先首先是在信息学中被提出,主要用来描述一个系统内部的混乱程度,也就是信息的“大小”。我们记录一个消息,有的消息比较长,需要用很多位数字才能记录,有的消息比较小,只需要几位就记下来了。一个消息需要多少位来记录?人们就发明了信息熵。
猜数字,第一个游戏是猜1-16中的一个。答题者先猜:是8以上的数字吗?出题者说:不是。那么可以锁定这个数字是在1-8之间。我们用0表示1-8中的一个数,用1表示9-16中的一个数,那么答题者记录下一个0。然后答题者猜:是4以上的数字吗?出题者说:是。我们用0表示1-4中的一个数,用1表示5-8中的一个数。那么答题者记录下一个1。然后答题者猜:是6以上的数字吗?出题者说:不是。答题者记录下0。答题者猜?是5吗?出题者说:是。答题者记录下1。所以答题者记录下来的是0101。答题者用4位信息,记录下了1-16中的一个数字。
对于二进制来说,N以内的数需要 l o g 2 N log_{2}N log2N位,对于十进制来说,N以内的数需要 l o g 10 N log_{10}N log10N 位,对于k进制来说,N以内的数需要 l o g k N log_{k}N logkN 位。( l o g 10 N = l o g 10 2 ∗ l o g 2 N log_{10}N = log_{10}2 * log_{2}N log10N=log102∗log2N)
从概率角度来分析猜游戏的例子:我们其实可以把猜中某个数字的所用的信息化为分别猜中1-16所用的信息信息,即 l o g 2 16 = 1 16 ∗ l o g 2 1 1 16 + 1 16 ∗ l o g 2 1 1 16 + . . . + 1 16 ∗ l o g 2 1 1 16 = ∑ p i l o g p i log_{2}16 = \frac{1}{16} * log_{2}\frac{1}{\frac{1}{16}} + \frac{1}{16} * log_{2}\frac{1}{\frac{1}{16}}+ ...+\frac{1}{16} * log_{2}\frac{1}{\frac{1}{16}}=\sum p_{i}logp_{i} log216=161∗log21611+161∗log21611+...+161∗log21611=∑pilogpi
(3)基尼系数(Gini):

G i n i ( t ) = 1 − ∑ i = 1 c p ( i ∣ t ) 2 Gini(t) = 1-\sum_{i=1}^c p(i|t)^2 Gini(t)=1−i=1∑cp(i∣t)2
G i n i ( B ) = ∣ B 1 ∣ ∣ A ∣ G i n i ( B 1 ) + ∣ B 2 ∣ ∣ A ∣ G i n i ( B 2 ) Gini(B) = \frac{|B_1|}{|A|}Gini(B_1)+\frac{|B_2|}{|A|}Gini(B_2) Gini(B)=∣A∣∣B1∣Gini(B1)+∣A∣∣B2∣Gini(B2)
其中 ∣ B i ∣ ∣ A ∣ 为子数据集 B i 数据个数占父类数据集 A 中数据个数的比例。 其中\frac{|B_i|}{|A|}为子数据集B_i数据个数占父类数据集A中数据个数的比例。 其中∣A∣∣Bi∣为子数据集Bi数据个数占父类数据集A中数据个数的比例。
CART树默认选择Gini系数作为评估指标。
一、Bagging:随机森林(RandomForest)
1、概念
从提供的数据中随机抽样出不同的子集,用于建立多棵不同的决策树,并按照Bagging的规则对多棵决策树的结果进行集成(回归则平均,分类则少数服从多数)。以分类任务为例,新的输入样本进入,就让森林中的每一棵决策树分别进行判断和分类,每个决策树会得到一个自己的分类结果,决策树的分类结果中哪一个分类最多,那么随机森林就会把这个结果当做最终的结果。
2、算法流程
-
一个样本容量为N的样本,有放回的抽取N次,每次抽取1个,最终形成了N个样本。这选择好的N个样本用来训练一个决策树,作为决策树根节点处的样本;
-
当每个样本有M个属性时,在决策树的每个节点需要分裂时,随机从这M个属性中选取出m个属性,满足条件m << M。然后从这m个属性中采用某种策略(比如说信息增益)来选择1个属性作为该节点的分裂属性;
-
决策树形成过程中每个节点都要按照步骤2来分裂,一直到不能够再分裂为止;
-
按照步骤1~3建立大量的决策树,这样就构成了随机森林了。
(1)根节点(root node):没有入边,但有零条或者多条出边的点;
(2)内部点(internal node):只有一条入边并且有两条或多条出边的点;
(3)叶节点(leaf node):只有入边但没有出边的点;(4)分裂:在决策树的训练过程中,需要一次次的将训练数据集分裂成两个子数据集,这个过程就叫做分裂;
(5)信息增益:一个特征能够为分类系统带来多少信息,带来的信息越多,说明该特征越重要,相应的信息增益也就越大。
3、优点&缺点
-
优点
-
它可以处理很高维度(特征很多)的数据,并且不用降维,无需做特征选择;
-
它可以判断特征的重要程度(信息增益);
-
可以判断出不同特征之间的相互影响(一个特征承接一个特征建树);
-
不容易过拟合;
-
训练速度比较快,容易做成并行方法;
-
实现起来比较简单;
-
对于不平衡的数据集来说,它可以平衡误差;
-
如果有很大一部分的特征遗失,仍可以维持准确度。
-
-
缺点
- 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合;
- 对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的;
- 由于随机林使用许多决策树,因此在较大的项目上可能需要大量内存。这可以使它比其他一些更有效的算法慢。
4、基于Bagging算法的几点思考
4.1 为什么Bagging算法的效果一般比单个评估器更好?
泛化误差是模型在未知数据集上的误差,更低的泛化误差是所有机器学习/深度学习建模的根本目标。在机器学习当中,泛化误差一般被认为由偏差、方差和噪音构成。其中偏差是预测值与真实值之间的差异,衡量模型的精度。方差是模型在不同数据集上输出的结果的方差,衡量模型稳定性。噪音是数据收集过程当中不可避免的、与数据真实分布无关的信息。
当算法是回归算法、且模型衡量指标是MSE时,模型的泛化误差可以有如下定义:
泛化误差 = 偏 差 2 + 方差 + 噪 音 2 = b i a s 2 + v a r i a n c e + n o i s e 2 \begin{aligned} 泛化误差 &= 偏差^2 + 方差 + 噪音^2 \\ &= bias^2 + variance + noise^2 \end{aligned} 泛化误差=偏差2+方差+噪音2=bias2+variance+noise2
误差:反映的是整个模型的准确度;
Bias:反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度;
Variance:反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
Bagging的基本思想是借助弱评估器之间的“独立性”来降低方差,从而降低整体的泛化误差。这个思想可以被推广到任意并行使用弱分类器的算法或融合方式上,极大程度地左右了并行融合方式的实际使用结果。
Q1 :bagging算法输出结果的方差一定小于弱评估器输出结果的方差?(针对回归问题)
假设任意树输出的方差 V a r ( X i ) = σ 2 Var(X_i) = \sigma^2 Var(Xi)=σ2,则有:
V a r ( X ˉ ) = V a r ( 1 n ∑ i = 1 n X i ) = 1 n 2 V a r ( ∑ i = 1 n X i ) = 1 n 2 ( V a r ( X 1 ) + V a r ( X 2 ) + . . . + V a r ( X n ) ) = 1 n 2 n σ 2 = σ 2 n \begin{aligned} Var(\bar{X}) &= Var\left(\frac{1}{n}\sum_{i=1}^{n}X_i\right)\\ &= \frac{1}{n^2}Var\left(\sum_{i=1}^{n}X_i\right)\\ &= \frac{1}{n^2} \left( Var(X_1) + Var(X_2) + ... + Var(X_n) \right)\\ &= \frac{1}{n^2}n\sigma^2\\ &= \frac{\sigma^2}{n} \end{aligned} Var(Xˉ)=Var(n1i=1∑nXi)=n21Var(i=1∑nXi)=n21(Var(X1)+Var(X2)+...+Var(Xn))=n21nσ2=nσ2
Q2:bagging算法输出结果的方差一定小于弱评估器输出结果的方差?(针对分类问题,输出函数采用逻辑回归函数)
当()为二阶可导函数时,根据泰勒展开( f ( X ˉ ) 在 E ( X ˉ ) f(\bar{X})在E(\bar{X}) f(Xˉ)在E(Xˉ)处展开)我们可以有:
f ( X ˉ ) ≈ f ( E ( X ˉ ) ) + f ′ ( E ( X ˉ ) ) ( A − E ( X ˉ ) ) V a r ( f ( X ˉ ) ) ≈ f ′ ( E ( X ˉ ) ) 2 V a r ( X ˉ ) = f ′ ( E ( X ˉ ) ) 2 ∗ σ 2 n \begin{align} f(\bar{X})\approx f(E(\bar{X} )) + f' {(E(\bar{X} ))} (A-E(\bar{X}))\\ Var(f(\bar{X}))\approx f' {(E(\bar{X} ))}^{2} Var(\bar{X})\\ =f' {(E(\bar{X} ))}^{2} * \frac{\sigma ^{2}}{n} \end{align} f(Xˉ)≈f(E(Xˉ))+f′(E(Xˉ))(A−E(Xˉ))Var(f(Xˉ))≈f′(E(Xˉ))2Var(Xˉ)=f′(E(Xˉ))2∗nσ2
式子的第一部分是sigmoid函数一阶导数的平方,sigmoid函数的一阶导数的取值范围为[0,0.25],因此无论 E [ X ˉ ] E[\bar{X}] E[Xˉ]是怎样的一个值,该式子的前半部分一定是一个位于范围[0,0.0625]的数。
4.2 Bagging的效果总是强于弱评估器吗?
Bagging当然不总是有效的,Bagging能够提升模型效果的条件有以下三个:
- 1、弱评估器的偏差较低,特别地来说,弱分类器的准确率至少要达到50%以上;
- 2、弱评估器之间相关性弱,最好相互独立;
- 3、弱评估器是方差较高的评估器。
解释第一点
在分类的例子中,假设我们建立了25棵树,对任何一个样本而言,平均或多数表决原则下,当且仅当有13棵以上的树判断错误的时候,随机森林才会判断错误。假设单独一棵决策树在样本i上的分类准确率在0.8上下浮动,那一棵树判断错误的概率大约就有0.2(ε),那随机森林判断错误的概率(有13棵及以上的树都判断错误的概率)是: e r a n d o m _ f o r e s t = ∑ i = 13 25 C 25 i ε i ( 1 − ε ) 25 − i = 0.000369 e_{random\_forest} = \sum_{i=13}^{25}C_{25}^{i}\varepsilon^{i}(1-\varepsilon)^{25-i} = 0.000369 erandom_forest=∑i=1325C25iεi(1−ε)25−i=0.000369
import numpy as np from scipy.special import comb#专门用来计算组合 np.array([comb(25,i)*(0.2**i)*((1-0.2)**(25-i)) for i in range(13,26)]).sum() # output:0.00036904803455582827可视化弱分类器的准确率至少要达到50%以上, bagging算法才有效
import numpy as np x = np.linspace(0,1,20) y = [] for epsilon in np.linspace(0,1,20): E = np.array([comb(25,i)*(epsilon**i)*((1-epsilon)**(25-i)) for i in range(13,26)]).sum() y.append(E) plt.plot(x,y,"o-") plt.plot(x,x,"--",color="red") plt.xlabel("individual estimator's error") plt.ylabel("RandomForest's error") plt.grid() plt.show()output:
分析:当基分类器的误差率小于0.5,即准确率大于0.5时,集成的效果是比弱分类器要好的。相反,当基分类器的误差率大于0.5,袋装的集成算法就失效了。所以在使用随机森林之前,一定要检查,用来组成随机森林的分类树是否都有至少50%的预测正确率。
解释第二&三点
虽然很难保证所有的弱评估器很难完全相互独立(所有弱评估器都是在相同的数据集上进行取样训练的),但我们可以根据随机森林输出的结果的方差来判断弱评估器之间相关性大小。
V a r ( X ˉ ) = V a r ( X 1 + X 2 + . . . + X n n ) = σ 2 n + 1 n 2 C n 2 C o v ( X i , X j ) = σ 2 n + 2 ∗ 1 n 2 ∗ n ∗ ( n − 1 ) 2 ∗ ρ ∗ σ 2 = σ 2 n + n − 1 n ∗ ρ ∗ σ 2 \begin{align} Var(\bar{X}) &= Var(\frac{X_{1} + X_{2} + ...+X_{n}}{n})\\ &= \frac{\sigma ^{2}}{n} + \frac{1}{n^{2}}C_{n}^{2}Cov(X_{i}, X_{j})\\ &= \frac{\sigma ^{2}}{n} + 2 * \frac{1}{n^{2}}* \frac{n*(n-1)}{2} *\rho *\sigma ^{2}\\ &= \frac{\sigma ^{2}}{n} + \frac{n-1}{n} *\rho *\sigma ^{2} \end{align} Var(Xˉ)=Var(nX1+X2+...+Xn)=nσ2+n21Cn2Cov(Xi,Xj)=nσ2+2∗n21∗2n∗(n−1)∗ρ∗σ2=nσ2+nn−1∗ρ∗σ2
弱评估器之间的相关性越强,随机森林输出的结果的方差就越大,Bagging方法通过降低方差而获得的泛化能力就越小。因此Bagging方法擅长处理方差大、偏差低的模型,而不擅长处理方差小、偏差大的模型。*对于任意算法而言,方差与偏差往往不可兼得,这也很容易理解——*想要在当前数据集上获得低偏差,必然意味着需要重点学习当前数据集上的规律,就不可避免地会忽略未知数据集上的规律,因此在不同数据集上进行测试时,模型结果的方差往往很大。
4.3 Bagging方法可以集成决策树之外的算法吗?
强大又复杂的算法(非线性或者非参数化的算法)如决策树、支持向量机、KNN等,往往学习能力较强,倾向于表现为偏差低、方差高,这些算法就比较适合于Bagging。而线性回归、逻辑回归等复杂度较低的算法(线性或者参数化的算法),学习能力较弱(需要迭代多轮)但表现稳定,因此倾向于表现为偏差高,方差低,就不太适合被用于Bagging。
4.4 怎样增强Bagging中弱评估器的独立性?
在随机森林中,可以使用“随机性”来削弱弱分类器之间的联系、增强独立性、提升随机森林的效果,随机森林算法天生就存在有放回随机抽取样本建树的机制,可以在袋外数据(验证集)上对模型性能进行评估,同时也可以对max_features超参数进行设置从而对数模型进行粗剪枝。
RandomForest中,是可以放回抽样的,一般情况下max_samples=m(样本量), 由洛必达法则可知,当样本量m足够大时,$1-(1-\frac{1}{m})^{m} $ -> 1-(1/e), 因此会有约37%的训练数据被浪费掉,没有参与建模,这些数据被称为袋外数据(out of bag data,简写为oob)。在实际使用随机森林时,袋外数据常常被我们当做验证集使用。
5、代码实操
5.1 自编程实现RandomForest
# -*- coding: utf-8 -*-
import csv
from random import seed
from random import randrange
from math import sqrt
def loadCSV(filename): # 加载数据,一行行的存入列表
'''
##作用
将csv的每行数据都用list格式读取出来,并未对其转换为int格式
##params
filename:要读取的文件名
##return
dataset:每行数据都是list形式,每个元素都是str格式
'''
dataSet = []
with open(filename, 'r') as file:
csvReader = csv.reader(file)
# reader返回的值是csv文件中每行数据的列表,将每行读取的值作为列表返回
for line in csvReader:
dataSet.append(line)
return dataSet
# 除了标签列,其他列都转换为float类型
def column_to_float(dataSet):
'''
##作用
对读取后的每个数据(除label)的数据类型从str变为float
##input
1、dataSet:
维度:208 * 61
每个元素都是str格式
##修改后
1、将dataSet的每个元素(除label)由str格式变为float格式
2、维度:208 * 61
'''
featLen = len(dataSet[0]) - 1
for data in dataSet:
for column in range(featLen):
data[column] = float(data[column].strip())
#原本csv.reader中的数据都是带引号的,需要将其转化为float数据,去除引号
# 将数据集随机分成N块,方便交叉验证,其中一块是测试集,其他四块是训练集
def spiltDataSet(dataSet, n_folds):
'''
## 作用
将原数据集随机分成5份(样本不会重复),每份维度:41 * 61
##input
1、dataSet:{维度:208 * 61,描述:除label外各个元素都是float类型}
2、n_fold:将数据集分成几份
##output
数据集分成n_fold份后的list类型
'''
fold_size = int(len(dataSet) / n_folds)
dataSet_copy = list(dataSet)
dataSet_spilt = []
for i in range(n_folds):
fold = []
while len(fold) < fold_size:
# 这里不能用if,if只是在第一次判断时起作用,while执行循环,直到条件不成立
# 条件:fold中要有41个数据
index = randrange(len(dataSet_copy))
# randrange() 方法返回指定递增基数集合中的一个随机数
# e.g.:从 0-99 选取一个随机数
# print ("randrange(100) : ", random.randrange(100))
# 有事index的值不是完全按照randrange(208)的顺序,有时会跳掉几个,因为208太大了
fold.append(dataSet_copy.pop(index)) # pop() 函数用于移除列表中的一个元素(默认最后一个元素),并且返回该元素的值。
dataSet_spilt.append(fold)
return dataSet_spilt
# 构造数据子集(从dataSet中放回地抽取164个样本,维度164*61)
def get_subsample(dataSet, ratio):
'''
##作用
从dataSet中放回地一个一个地抽取(len(dataSet) * ratio)个数据组成list(维度:164*61)
##paras
1、dataSet:去除row,sum过的数据集(维度:164*61)
2、ratio:dataSet中放回地一个一个地抽取数据的比率
##output
1、subdataSet:抽样得到的数据集(维度:164*61)
'''
subdataSet = []
lenSubdata = round(len(dataSet) * ratio) # 返回浮点数
while len(subdataSet) < lenSubdata:
index = randrange(len(dataSet))
subdataSet.append(dataSet[index])
# print len(subdataSet)
return subdataSet
# 分割数据集
def data_spilt(dataSet, index, value):
'''
##作用
分支--遍历dataSet中的每条数据,看每条数据的第index属性值跟value作比较,从而决定该条数据是进入左枝还是右枝
##params
1、dataSet:除row,sum过的数据集(维度:164*61)
2、index:随机抽取的n_features个特征中的一个
3、value:分支的阈值--遍历选取的dataSet中某条数据第index个属性值
##return
left,right:遍历dataSet中的每条数据,看每条数据的第index属性值跟value作比较,从而决定该条数据是进入左枝还是右枝,小于则进入左枝
'''
left = []
right = []
for row in dataSet:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# 计算分割代价
def spilt_loss(left, right, class_values):
'''
##作用
利用传进来的已经分类好的左枝和右枝数据,计算在不同label下的Gini系数
注:两个label下Gini系数相同
## params
1、left:左枝存储的数据集
2、right:右枝存储的数据集
3、class_values:【‘M','R']
##return
Gini系数
'''
loss = 0.0
for class_value in class_values:
left_size = len(left)
right_size = len(right)
if left_size != 0: # 防止除数为零
prop = [row[-1] for row in left].count(class_value) / float(left_size)
loss += 2 * (prop * (1.0 - prop)) * (left_size / (left_size + right_size)) #计算基尼系数
if right_size != 0:
prop = [row[-1] for row in right].count(class_value) / float(right_size)
loss += 2 * (prop * (1.0 - prop)) * (right_size / (left_size + right_size))
return loss
# 选取任意的n个特征,在这n个特征中,选取分割时的最优特征
def get_best_spilt(dataSet, n_features):
'''
##作用
1、选取任意的n_features个特征;
2、在这n_features个特征中,遍历每一个随机选取特征下的dataSet中的每一条数据,选取分割时的最优特征
##params
1、dataSet:除row,sum过的数据集(维度:164*61)
2、n_features:随机抽取(有放回地)的特征个数
##return
返回字典,字典里分别存储{最优特征,特征值(分裂用),左枝的数据,右枝的数据}
'''
features = []
class_values = list(set(row[-1] for row in dataSet)) # set()将所有label去重
b_index, b_value, b_loss, b_left, b_right = 999, 999, 999, None, None # 初始化参数值
while len(features) < n_features:
index = randrange(len(dataSet[0]) - 1)
if index not in features:
features.append(index)
# print 'features:',features
# 遍历每一个随机选取特征下的dataSet中的每一条数据
for index in features: # 找到列的最适合做节点的索引,(损失最小)
for row in dataSet:
left, right = data_spilt(dataSet, index, row[index]) # 以它为节点的,左右分支
loss = spilt_loss(left, right, class_values)
if loss < b_loss: # 寻找最小分割代价
b_index, b_value, b_loss, b_left, b_right = index, row[index], loss, left, right
# print b_loss
# print type(b_index)
return {'index': b_index, 'value': b_value, 'left': b_left, 'right': b_right}
# 决定输出标签
def decide_label(data):
'''
##作用
对数据进行表标签
##params
data:传入的数据集(带最后一列)
##return
label:‘M'或者’R‘
'''
output = [row[-1] for row in data]
return max(set(output), key=output.count) # 就以key的函数对象为判断的标准
#set()具有和集合一样的作用:去重
# 子分割,不断地构建叶节点的过程
def sub_spilt(root, n_features, max_depth, min_size, depth):
'''
##作用
以递归的方式建立分类树
##params
1、root:只确定了根节点和分裂标准的树,以字典形式存储
2、n_features:随机抽取(有放回地)的特征个数
3、max_depth:分类树的最大深度
4、min_size:分割内部节点所需的最小样本数,当叶子节点最少的样本数
5、depth:当前所要分裂的节点所在的深度
##return
无return,只是在原来root的基础上进行修改
'''
left = root['left']
# print left
right = root['right']
# del (root['left']) # 有没有del 都可以
# del (root['right'])
# print depth
# 多分支后有一个枝叶子节点没有样本,则表明上一个节点里的样本数都是大于等于或小于阈值,则可以直接表标签
if not left or not right:
root['left'] = root['right'] = decide_label(left + right)
# print 'testing'
return #作用是强制结束函数的调用过程,并且返回调用者现场类似于break的作用
# 当树的深度大于10(max_depth=10),此处决策树不能再分支下去
if depth > max_depth:
root['left'] = decide_label(left)
root['right'] = decide_label(right)
return
# 当某个叶子节点的样本数<1时,需要对其进行label的确定
# if len(left) < min_size:
# root['left'] = decide_label(left)
# else:
# 此步骤与 if not left or not right:
# root['left'] = root['right'] = decide_label(left + right)重复
root['left'] = get_best_spilt(left, n_features)
# print 'testing_left'
sub_spilt(root['left'], n_features, max_depth, min_size, depth + 1)
# if len(right) < min_size:
# root['right'] = decide_label(right)
# else:
root['right'] = get_best_spilt(right, n_features)
# print 'testing_right'
sub_spilt(root['right'], n_features, max_depth, min_size, depth + 1)
# 构造决策树
def build_tree(dataSet, n_features, max_depth, min_size):
'''
##作用
生成一棵完整的分类树
##params
1、dataSet:切割的数据集中选取子集(从dataSet中放回地抽取164个样本,维度164*61)
2、n_features:随机抽取(有放回地)的特征个数
3、max_depth:分类树的最大深度、
4、min_size:分割内部节点所需的最小样本数,当叶子节点最少的样本数
##retrun
完整的分类树(字典形式)
'''
root = get_best_spilt(dataSet, n_features) # 确定每一段子树的根节点以及具体的n_features个特征
sub_spilt(root, n_features, max_depth, min_size, 1)
return root
# 预测测试集结果
def predict(tree, row):
'''
##作用
对row里的数据,走一遍单个tree的结构,判断它的label是‘M' or ’S‘
##params
1、tree:完整的树的结构(字典形式)
2、row:test(测试集)的每一条数据
##return:
label:‘M' or ’S‘
'''
predictions = []
if row[tree['index']] < tree['value']:
if isinstance(tree['left'], dict):
return predict(tree['left'], row)
else:
return tree['left']
else:
if isinstance(tree['right'], dict):
return predict(tree['right'], row)
else:
return tree['right']
# predictions=set(predictions)
def bagging_predict(trees, row):
'''
##作用
对row里的每一条数据,走一遍10个tree的结构,多数表决准则判断它的label是‘M' or ’S‘
##params
1、tree:完整的十个树的结构(字典形式)
2、row:test(测试集)的每一条数据
##return:
label:‘M' or ’S‘
'''
predictions = []
predictions = [predict(tree, row) for tree in trees]
return max(set(predictions), key=predictions.count)
# 创建随机森林
def random_forest(train, test, ratio, n_features, max_depth, min_size, n_trees):
'''
##作用
##params
1、train:去掉row且sum过的数据集,维度:164*61
2、test:仅有row的数据集,维度:41*61
3、n_feature:特征数
4、ratio:从train中选取的样本比列
5、max_depth:树的最大深度
6、min_size:分割内部节点所需的最小样本数,当叶子节点最少的样本数
7、n_trees:决策树的棵树
##output
1、test中每条数据的预测结果(以list形式储存)
'''
trees = []
for i in range(n_trees):
tran = get_subsample(train, ratio) # 从切割的数据集中选取子集(从dataSet中放回地抽取164个样本,维度164*61)
tree = build_tree(tran, n_features, max_depth, min_size)
# print 'tree %d: '%i,tree
trees.append(tree)
# predict_values = [predict(trees,row) for row in test]
predict_values = [bagging_predict(trees, row) for row in test]
return predict_values
# 计算准确率
def accuracy(predict_values, actual):
'''
##作用
通过比对predict_values 和 actual两个列表中每一个元素计算准确率
##params
1、predict_values:预测值(list形式)
2、actual:真实值(list形式)
##return
预测准确率
'''
correct = 0
for i in range(len(actual)):
if actual[i] == predict_values[i]:
correct += 1
return correct / float(len(actual))
if __name__ == '__main__':
seed(1) # random.random该方法返回的是[0,1)之间的小数,是包含0但是不包含1,左开又闭区间
# 与后面的randrange()函数一起用,根据你在seed()中传入的参数不同,seed会构建一个元素不同的列表,
# 而random.randrange()会迭代这个列表,按照列表的顺序将每个元素依次提出来作为随机数算法的初始值。‘
# 这也就是为什么在例子1中设置了一个seed()后每次返回的随机序列都是相同的
# 后面外部函数里的randrange()两次返回的结果都不同,即使randrange()里的值相同
# 详见csdn:对random.seed()的理解
# 取数据(维度:208*61),最后一列为label
dataSet = loadCSV(r'C:\Users\AlexChan\Documents\XTU\李航-机器学习方法\深度之眼\监督学习\代码'
r'\Statistical-Learning-Method_Code-master'
r'\Statistical-Learning-Method_Code-master\RandomForest\data\sonar-all-data.csv')
column_to_float(dataSet) # dataSet
# 作用:loadCSV读出的数据都是string格式,需要将其转化为float格式(都不是int),并将两边空格删去,对于label列不需要转换
# 维度:208 * 61
n_folds = 5
max_depth = 15
min_size = 1
ratio = 1.0
n_features=round(sqrt(len(dataSet[0])-1))
#从所有属性(去掉最后一列label)中选取属性个数:根号下的源数据集的特征数(61-1)
n_trees = 10
folds = spiltDataSet(dataSet, n_folds) # 先是切割数据集
# 作用:1、将原数据集随机分成5份(样本可能会重复),每份维度:41 * 61
# 2、交叉验证5次
# folds的维度:5 * 41 * 61
scores = []
for fold in folds:
# fold维度:41 * 61
train_set = folds[:]
# 此处不能简单地用train_set=folds,这样用属于引用,那么当train_set的值改变的时候,folds的值也会改变,所以要用复制的形式。
# (L[:])能够复制序列,D.copy() 能够复制字典,list能够生成拷贝 list(L)
train_set.remove(fold) # 选好训练集
# train_set的维度:4 * 41 * 61
# print len(folds)
train_set = sum(train_set, []) # 将多个fold列表组合成一个train_set列表
# 将最内层的list拼在一起,中间用逗号分开
# ['a','b','c','d'], ['e','f','g']], [])--输出: ['a', 'b', 'c', 'd', 'e', 'f', 'g']
# train_set维度:164 * 61
# print len(train_set)
test_set = []
for row in fold:
# fold维度:41 * 61
# row维度:1 * 61
row_copy = list(row)
#list作用:是row_copy和row的id不同
row_copy[-1] = None
# 将label改为None
test_set.append(row_copy)
# for row in test_set:
# print row[-1]
# test_set维度:41 * 61(最后一列label为None)
actual = [row[-1] for row in fold]
# 将最后一列(label)数据放在actual的list中
# 注意:这里是从fold中提取label,前面只对row_copy的最后一列变为None
# actual维度:1 * 41
predict_values = random_forest(train_set, test_set, ratio, n_features, max_depth, min_size, n_trees)
# {train_set维度:164 * 61, test_set维度:41 * 61, ratio:1.0,n_features=15,max_depth=15
# 此时train_set中是没有row(row维度41 * 61 ),而test_set中存储的就是row
accur = accuracy(predict_values, actual)
scores.append(accur)
print('Trees is %d' % n_trees)
print('scores:%s' % scores)
print('mean score:%s' % (sum(scores) / float(len(scores))))
'''
训练部分:假设我们取dataset中的m个feature来构造决策树,首先,我们遍历m个feature中的每一个feature,再遍历每一行,
通过spilt_loss函数(计算分割代价)来选取最优的特征及特征值,根据是否大于这个特征值进行分类(分成left,right两类),循环执行上述步骤,
直至不可分或者达到递归限值(用来防止过拟合),最后得到一个决策树tree。
测试部分:对测试集的每一行进行判断,决策树tree是一个多层字典,每一层为一个二分类,将每一行按照决策树tree中的分类索引index一步一步向里层探索,
直至不出现字典时探索结束,得到的值即为我们的预测值。
'''
5.2 调用sklearn库实现RandomForest
class sklearn.ensemble.RandomForestRegressor(n_estimators=100, *, criterion=‘squared_error’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=‘auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, ccp_alpha=0.0, max_samples=None)
class sklearn.ensemble.RandomForestClassifier(n_estimators=100, *, criterion=‘gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=‘auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None)
| 类型 | 参数 |
|---|---|
| 弱分类器数量 | n_estimators:迭代次数/决策树数目 |
| 弱分类器的训练数据 | bootstrap:是否对样本进行随机抽样 oob_score:如果使用随机抽样,是否使用袋外数据作为验证集 max_samples:如果使用随机抽样,每次随机抽样的样本量 max_features:随机抽取特征的数目 random_state:控制一切随机模式 |
| 弱分类器结构 | criterion:弱评估器分枝时的不纯度衡量指标 max_depth:弱评估器被允许的最大深度,默认None min_samples_split:弱评估器分枝时,父节点上最少要拥有的样本个数 min_samples_leaf:弱评估器的叶子节点上最少要拥有的样本个数 min_weight_fraction_leaf:当样本权重被调整时,叶子节点上最少要拥有的样本权重 max_leaf_nodes:弱评估器上最多可以有的叶子节点数量 min_impurity_decrease:弱评估器分枝时允许的最小不纯度下降量 |
| 其他 | n_jobs:允许调用的线程数 verbose:打印建树过程 ccp_alpha:结构风险$ |
| 影响力 | 参数 |
|---|---|
| ⭐⭐⭐⭐⭐ 几乎总是具有巨大影响力 |
n_estimators(整体学习能力) max_depth(粗剪枝) max_features(随机性) |
| ⭐⭐⭐⭐ 大部分时候具有影响力 |
max_samples(随机性) class_weight(样本均衡) |
| ⭐⭐ 可能有大影响力 大部分时候影响力不明显 |
min_samples_split(精剪枝) min_impurity_decrease(精剪枝) max_leaf_nodes(精剪枝) criterion(分枝敏感度) |
| ⭐ 当数据量足够大时,几乎无影响 |
random_state ccp_alpha(结构风险) |
# 导入相关库(code)
import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import time #计时模块time
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold, GridSearchCV
def RMSE(cvresult,key):
'''
计算训练集和测试集上的均方根误差
'''
return (abs(cvresult[key])**0.5).mean()
# 导入数据
data = pd.read_csv("train_encode.csv",index_col=0)
# 提取特征数据和标签数据
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
# 初始化随机种子为1412的随机森林回归评估器(使用默认参数)
reg = RFR(random_state=1412)
# 初始化随机种子为1412五折交叉验证评估器
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
# 对数据集进行五折交叉验证评估器训练
result_pre_adjusted = cross_validate(reg,X,y,cv=cv,scoring="neg_mean_squared_error"
,return_train_score=True
,verbose=True
,n_jobs=-1)
# 以调用函数的形式返回训练集和测试集上的均方根误差
RMSE(result_pre_adjusted,"train_score")# output:11177.272008319653
RMSE(result_pre_adjusted,"test_score")# 30571.26665524217
# 创建超参数空间
param_grid_simple = {"criterion": ["squared_error","poisson"]
, 'n_estimators': [*range(20,100,5)]
, 'max_depth': [*range(10,25,2)]
, "max_features": ["log2","sqrt",16,32,64,"auto"]
, "min_impurity_decrease": [*np.arange(0,5,10)]
}
# 实例化用于搜索的评估器、交叉验证评估器与网格搜索评估器
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
search = GridSearchCV(estimator=reg
,param_grid=param_grid_simple
,scoring = "neg_mean_squared_error"
,verbose = True
,cv = cv
,n_jobs=-1)
# 训练网格搜索评估器
start = time.time()
search.fit(X,y)
print(time.time() - start)
# 查看结果:超参数和验证集上的均方根误差
search.best_estimator_
abs(search.best_score_)**0.5
稍微提及极端随机树
与随机森林一样,极端随机树在建树时会随机挑选特征,但不同的是,随机森林会将随机挑选出的特征上每个节点都进行完整、精致的不纯度计算,然后挑选出最优节点,而极端随机树则会随机选择数个节点进行不纯度计算,然后选出这些节点中不纯度下降最多的节点。这样生长出的树比随机森林中的树更不容易过拟合,同时独立性更强,因此极端随机树可以更大程度地降低方差。
当然了,这种手段往往也会带来偏差的急剧下降,因此极端随机树是只适用于方差过大、非常不稳定的数据的。除非特殊情况,我们不会考虑使用极端随机树,但了解这个算法的存在也是一件好事。
二、Boosting:AdaBoost算法
1、介绍
在以随机森林为代表的Bagging算法中,我们一次性建立多个平行独立的弱评估器,并让所有评估器并行运算。在Boosting集成算法当中,我们逐一建立多个弱评估器(基本是决策树),并且下一个弱评估器的建立方式依赖于上一个弱评估器的评估结果,最终综合多个弱评估器的结果进行输出,因此Boosting算法中的弱评估器之间不仅不是相互独立的、反而是强相关的,同时Boosting算法也不依赖于弱分类器之间的独立性来提升结果,Boosting的不同算法之间的核心区别就在于上一个弱评估器的评估结果具体如何影响下一个弱评估器的建立过程。
- Boosting算法的基本元素和核心思想
- 三大基本元素
- 损失函数 L ( x , y ) L(x,y) L(x,y) :用以衡量模型预测结果与真实结果的差异;
- 弱评估器 f ( x ) f(x) f(x) :(一般为)决策树,不同的boosting算法使用不同的建树过程;
- 综合集成结果 H ( x ) H(x) H(x):即集成算法具体如何输出集成结果。
- 核心思想
- 依据上一个弱评估器 f ( x ) t − 1 f(x)_{t-1} f(x)t−1的结果,计算损失函数 L ( x , y ) L(x,y) L(x,y),
并使用 L ( x , y ) L(x,y) L(x,y)自适应地影响下一个弱评估器 f ( x ) t f(x)_t f(x)t的构建。集成模型输出的结果,受到整体所有弱评估器 f ( x ) 0 f(x)_0 f(x)0 ~ f ( x ) T f(x)_T f(x)T的影响。
- 依据上一个弱评估器 f ( x ) t − 1 f(x)_{t-1} f(x)t−1的结果,计算损失函数 L ( x , y ) L(x,y) L(x,y),
- 三大基本元素
- Boosting Vs Bagging
| 装袋法 Bagging | 提升法 Boosting | |
|---|---|---|
| 弱评估器 | 相互独立,并行构建 | 相互关联,按顺序依次构建 先建弱分类器的预测效果影响后续模型的建立 |
| 建树前的抽样方式 | 样本有放回抽样 特征无放回抽样 |
样本有放回抽样 特征无放回抽样 |
| 集成的结果 | 回归平均 分类众数 |
每个算法具有自己独特的规则,一般来说: (1) 表现为某种分数的加权平均 (2) 使用输出函数 |
| 目标 | 降低方差 提高模型整体的稳定性来提升泛化能力 本质是从“平均”这一数学行为中获利 |
降低偏差 提高模型整体的精确度来提升泛化能力 相信众多弱分类器叠加后可以等同于强学习器 |
| 单个评估器容易 过拟合的时候 |
具有一定的抗过拟合能力 | 具有一定的抗过拟合能力 |
| 单个评估器的效力 比较弱的时候 |
可能失效(分类器是先建的话) | 大概率会提升模型表现 |
| 代表算法 | 随机森林 | 梯度提升树,Adaboost |
- sklearn中常见的boosting算法
- AdaBoost:自适应增强算法(Adaptive Boosting Algorithm / AdaBoost Algorithm)
- GBDT:梯度提升树(Gradient Boosting Decision Tree)
- XGBoost:极限提升树(Extreme Gradient Boosting Tree)
- LightGBM:轻量梯度提升树(Light Gradiant Boosting Machine)
- CatBoost:离散提升树(Categorial Boosting Tree)
2、AdaBoost
2.1 算法介绍
在这篇论文中(Multi-class AdaBoost), AdaBoost是首个成功将boosting思想发扬光大的算法。它的主要贡献在于实现了两个变化:
- 首次实现根据之前弱评估器的结果自适应地影响后续建模过程;
- 在Boosting算法中,首次实现考虑全部弱评估器结果的输出方式;
首先,Boosting算法在全样本上建立一棵决策树,根据该决策树预测的结果和损失函数值,增加被预测错误的样本在数据集中的样本权重,并让加权后的数据集被用于训练下一棵决策树。这个过程相当于有意地加重“难以被分类正确的样本”的权重,同时降低“容易被分类正确的样本”的权重,而将后续要建立的弱评估器的注意力引导到难以被分类正确的样本上。
在该过程中,上一棵决策树的的结果通过影响样本权重、即影响数据分布来影响下一棵决策树的建立,整个过程是自适应的。当全部弱评估器都被建立后,集成算法的输出 H ( x ) H(x) H(x)等于所有弱评估器输出值的加权平均,加权所用的权重也是在建树过程中被自适应地计算出来的。
2.2 算法流程
-
二分类:假设数据集$ T={X_{i}, y_{i}}, i=1,2,…,N, y_{i} \in \left { -1, 1 \right } $ ,h(x)为估计器,估计器的数量为K
- AdaBoost算法流程
-
初始化样本权重向量$ w_{1},其中w_{1,i} = \frac{1}{N},i=1,…,N $;
-
遍历估计器的数量 K 次:
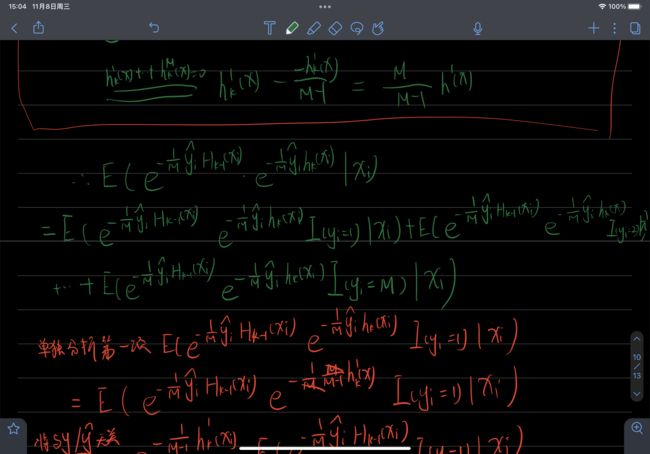
2-1. 在样本权重$ w_{k} 下训练估计器 h ( x ) ; 2 − 2. 计算第 k 次的误差率 下训练估计器h(x); 2-2. 计算第k次的误差率 下训练估计器h(x);2−2.计算第k次的误差率e_{k},如果e_{k}>0.5,则退出循环 ,其中 ,其中 ,其中 \mathrm{e}{\mathrm{k}}=\sum{\mathrm{i}=1}^{\mathrm{N}} \omega_{\mathrm{k}, \mathrm{i}} \mathrm{I}\left(\mathrm{y}{\mathrm{i}} \neq \mathrm{h}{\mathrm{k}}\left(\mathrm{X}_{\mathrm{i}}\right)\right)$;2-3. 计算第k次的估计器权重$ \alpha_{k} = \frac {1}{2} ln\frac {1 - e_{k}}{e_{k}}$;
2-4. 计算第k+1次的权重向量$ w_{k+1}, 其中w_{k+1,i} = \frac{w_{k, i}e{-y_{i}\alpha_{k}h_{k}(X_{i})}}{\sum_{j=1}{N}( w_{k,j}e^{-y_{j}\alpha_{k}h_{k}(X_{j})})}$;
-
采用加权后的结果去sign函数,得到最后的强估计器: H x = s i g n ( ∑ i = 1 K α i h i ( x ) ) H_{x}=sign(\sum_{i=1}^{K}\alpha_{i}h_{i}(x)) Hx=sign(∑i=1Kαihi(x))。
-
分类误差大于0.5代表当前的分类器是否比随机预测要好,对于一个随机预测模型来说,其分类误差就是0.5,即一半预测对,一半预测错。若当前的弱分类器还没有随机预测的效果好,那便直接终止算法。但是当adaboost遇到这种情形时可能学习的迭代次数远远没有达到初始设置的迭代次数M,这可能会导致最终集成中只有很少的弱分类器,从而导致算法整体性能不佳。
证明:
- AdaBoost算法流程
自编写代码实现
import numpy as np from sklearn.tree import DecisionTreeClassifier class adaboostc(): """ AdaBoost 分类算法 """ def __init__(self, n_estimators = 100): # AdaBoost弱学习器数量 self.n_estimators = n_estimators def fit(self, X, y): """ AdaBoost 分类算法拟合 """ # 初始化样本权重向量 sample_weights = np.ones(X.shape[0]) / X.shape[0] # 估计器数组 estimators = [] # 估计器权重数组 weights = [] # 遍历估计器 for i in range(self.n_estimators): # 初始化最大深度为1的决策树估计器 estimator = DecisionTreeClassifier(max_depth = 1) # 按照样本权重拟合训练集 estimator.fit(X, y, sample_weight=sample_weights) # 预测训练集 y_predict = estimator.predict(X) # 计算误差率 e = np.sum(sample_weights[y_predict != y]) # 当误差率大于等于0.5时跳出循环 if e >= 0.5: self.n_estimators = i break # 计算估计器权重 weight = 0.5 * np.log((1 - e) / e) # 计算样本权重 temp_weights = np.multiply(sample_weights, np.exp(- weight * np.multiply(y, y_predict))) # 归一化样本权重 sample_weights = temp_weights / np.sum(temp_weights) weights.append(weight) estimators.append(estimator) self.weights = weights self.estimators = estimators def predict(self, X): """ AdaBoost 分类算法预测 """ y = np.zeros(X.shape[0]) # 遍历估计器 for i in range(self.n_estimators): estimator = self.estimators[i] weight = self.weights[i] # 预测结果 predicts = estimator.predict(X) # 用fit方法中对于X和y已经训练好的self._estimators棵树 # 按照估计器的权重累加 y += weight * predicts # 根据权重的正负号返回结果 return np.sign(y)
-
多分类
假设训练集T={ X i , y i X_{i}, y_{i} Xi,yi},i=1, 2,…,N, $ y \in {1, 2, …, M} $ ,h(x)为估计器, 估计器的数量为K
-
AdaBoost-SUMME 算法流程
-
初始化样本权重向量$ w_{1},其中w_{1,i} = \frac{1}{N},i=1,…,N $;
-
遍历估计器的数量 K 次:
2-1. 在样本权重$ w_{k} 下训练估计器 h ( x ) ; 2 − 2. 计算第 k 次的误差率 下训练估计器h(x); 2-2. 计算第k次的误差率 下训练估计器h(x);2−2.计算第k次的误差率e_{k},如果e_{k}>0.5,则退出循环 ,其中 ,其中 ,其中 \mathrm{e}{\mathrm{k}}=\sum{\mathrm{i}=1}^{\mathrm{N}} \omega_{\mathrm{k}, \mathrm{i}} \mathrm{I}\left(\mathrm{y}{\mathrm{i}} \neq \mathrm{h}{\mathrm{k}}\left(\mathrm{X}_{\mathrm{i}}\right)\right)$;2-3. 计算第k次的估计器权重$ \alpha_{k} = ln\frac {1 - e_{k}}{e_{k}} + ln(M-1)$;
2-4. 计算第k+1次的权重向量$ w_{k+1}, 其中w_{k+1,i} = w_{k, i}e^{\alpha_{k}I(y_{i} \ne h_{k}(X_{i}))}$;
2-5. 权重向量$ w_{k+1} 进行归一化, 进行归一化, 进行归一化, w_{k+1,i} = \frac{w_{k+1,i}}{\sum_{j=1}^{N}(\overline w_{k+1, i})}$;
-
采用正确分类的结果加权后取值最大的分类,得到最后的强估计器: H x = a r g m a x m ( ∑ i = 1 K α i I ( y i = h k ( X i ) ) ) H_{x}=argmax_{m}(\sum_{i=1}^{K}\alpha_{i}I(y_{i} = h_{k}(X_{i}))) Hx=argmaxm(∑i=1KαiI(yi=hk(Xi)))。
-
-
证明:
自编程代码
import numpy as np from sklearn.tree import DecisionTreeClassifier class adaboostmc(): """ AdaBoost 多分类SAMME算法 """ def __init__(self, n_estimators = 100): # AdaBoost弱学习器数量 self.n_estimators = n_estimators def fit(self, X, y): """ AdaBoost 多分类SAMME算法拟合 """ # 标签分类 self.classes = np.unique(y) # 标签分类数 self.n_classes = len(self.classes) # 初始化样本权重向量 sample_weights = np.ones(X.shape[0]) / X.shape[0] # 估计器数组 estimators = [] # 估计器权重数组 weights = [] # 遍历估计器 for i in range(self.n_estimators): # 初始化最大深度为1的决策树估计器 estimator = DecisionTreeClassifier(max_depth = 1) # 按照样本权重拟合训练集 estimator.fit(X, y, sample_weight=sample_weights) # 训练集预测结果 y_predict = estimator.predict(X) incorrect = y_predict != y # 计算误差率 e = np.sum(sample_weights[incorrect]) # 计算估计器权重 weight = np.log((1 - e) / e) + np.log(self.n_classes - 1) # 计算样本权重 temp_weights = np.multiply(sample_weights, np.exp(weight * incorrect)) # 归一化样本权重 sample_weights = temp_weights / np.sum(temp_weights) weights.append(weight) estimators.append(estimator) self.weights = weights self.estimators = estimators def predict(self, X): """ AdaBoost 多分类SAMME算法预测 """ # 加权结果集合 results = np.zeros((X.shape[0], self.n_classes)) # 遍历估计器 for i in range(self.n_estimators): estimator = self.estimators[i] weight = self.weights[i] # 预测结果 predicts = estimator.predict(X) # dim:len(X),注意和predict_prob分清 # 遍历标签分类 for j in range(self.n_classes): # 对应标签分类的权重累加 results[predicts == self.classes[j], j] += weight # 取加权最大对应的分类作为最后的结果 return self.classes.take(np.argmax(results, axis=1), axis=0) # np.argmax(y_predict, axis=1):返回的是索引
-
AdaBoost-SUMME.R 算法流程:
-
初始化样本权重向量$ w_{1},其中w_{1,i} = \frac{1}{N},i=1,…,N $;
-
遍历估计器的数量 K 次
2-1. 在样本权重$ w_{k} 下计算加权概率估计向量 下计算加权概率估计向量 下计算加权概率估计向量 P_{k}^{m}(x)=P(y=m|x)$2-2. 计算第k+1次的权重向量$ w_{k+1}, 其中w_{k+1,i} = w_{k,i} e^{-\frac{M-1}{M} \hat{y_{i}^{T}}ln(P_{k}(x))}$
2-3. 对权重向量 w k + 1 , i w_{k+1,i} wk+1,i进行归一化, w k + 1 , i = w k + 1 , i ∑ j = 1 N w k + 1 , i ‾ w_{k+1,i}=\frac{w_{k+1,i}}{\sum_{j=1}^{N}\overline{w_{k+1, i}}} wk+1,i=∑j=1Nwk+1,iwk+1,i
-
采用概率估计计算结果取值最大的分类,得到最后的强估计器: H x = a r g m a x m ( ∑ i = 1 K h i ( x ) ) ,其中 h k ( x ) = ( M − 1 ) ( l n P k m ( x ) − 1 M ∑ i = 1 M l n P k i ( x ) ) H_{x}=argmax_{m}(\sum_{i=1}^{K}h_{i}(x)),其中h_{k}(x)=(M-1)(lnP_{k}^{m}(x)-\frac{1}{M}\sum_{i=1}^{M}lnP_{k}^{i}(x)) Hx=argmaxm(∑i=1Khi(x)),其中hk(x)=(M−1)(lnPkm(x)−M1∑i=1MlnPki(x))
-
自编程
# AdaBoost-SUMME.R 算法 import numpy as np from sklearn.tree import DecisionTreeClassifier import pandas as pd class adaboostmcr(): """ AdaBoost 多分类SAMME.R算法 """ def __init__(self, n_estimators = 100): # AdaBoost弱学习器数量 self.n_estimators = n_estimators def fit(self, X, y): """ AdaBoost 多分类SAMME.R算法拟合 """ # 标签分类 self.classes = np.unique(y) # 标签分类数 self.n_classes = len(self.classes) # 初始化样本权重 sample_weights = np.ones(X.shape[0]) / X.shape[0] # 估计器数组 estimators = [] # 论文中对 y 的定义 y_codes = np.array([-1. / (self.n_classes - 1), 1.]) # 将训练集中的标签值转换成论文中的矩阵形式 y_1 = y[:, np.newaxis] x_1 = self.classes == y[:, np.newaxis] y_coding = y_codes.take(self.classes == y[:, np.newaxis])# 构建权重矩阵,其维度为len(X) * self.n_classes, 类别正确,就是1; 错误就是-1. / (self.n_classes - 1) # 沿提到的轴和索引从数组返回elememts。True则取index=1的元素,否则取index=0的元素 # 遍历估计器 for i in range(self.n_estimators): # 初始化最大深度为1的决策树估计器 estimator = DecisionTreeClassifier(max_depth = 1) # 根据样本权重拟合训练集 estimator.fit(X, y, sample_weight=sample_weights) # 预测训练集标签值的概率 y_predict_proba = estimator.predict_proba(X) # 处理概率为0的结果,避免取对数是结果为负无穷大的问题 np.clip(y_predict_proba, np.finfo(y_predict_proba.dtype).eps, None, out=y_predict_proba) # np.finfo函数是根据括号中的类型来获得信息,获得符合这个类型的数型;将y_predict_proba数组中的值限制在[eps, None]范围内,eps是机器精度(这里是2.220446049250313e-16) # np.clip(a, a_min, a_max, out=None),其中a: 要进行限制操作的数组。a_min: 数组中的值不应小于的最小值。如果某个元素小于;a_min,则会被替换为a_min。a_max: 数组中的值不应大于的最大值。如果某个元素大于 # a_max,则会被替换为a_max。out: 可选参数,用于指定将结果存储在哪个数组。如果未提供ut,则将结果存储在新的数组中。则将结果存储在新的数组中 # 计算样本权重 temp_weights = sample_weights * np.exp(- ((self.n_classes - 1) / self.n_classes) * np.sum(np.multiply(y_coding, np.log(y_predict_proba)), axis=1)) # 归一化样本权重 sample_weights = temp_weights / np.sum(temp_weights) estimators.append(estimator) self.estimators = estimators def predict(self, X): """ AdaBoost 多分类SAMME.R算法预测 """ # 结果集合 results = np.zeros((X.shape[0], self.n_classes)) # 遍历估计器 for i in range(self.n_estimators): estimator = self.estimators[i] # 预测标签值的概率 y_predict_proba = estimator.predict_proba(X) # 同样需要处理零概率的问题 np.clip(y_predict_proba, np.finfo(y_predict_proba.dtype).eps, None, out=y_predict_proba) # 对概率取对数 y_predict_proba_log = np.log(y_predict_proba) # 计算 h(x) h = (self.n_classes - 1) * (y_predict_proba_log - (1 / self.n_classes) * np.sum(y_predict_proba_log, axis=1)[:, np.newaxis]) # np.sum(y_predict_proba_log, axis=1)[:, np.newaxis]:相当于把ndarray(8, )维度变为ndarray(8,1 ) # 累加 results += h # 取累加最大对应的分类作为最后的结果 result= self.classes.take(np.argmax(results, axis=1)) return self.classes.take(np.argmax(results, axis=1)) X = np.array([[1, 1], [2, 2], [2, 1], [1, 2], [1, 1], [1, 2], [1, 2], [2, 1]]) y = np.array([0, 2, 0, 1, 0, 1, 1, 2]) clf = adaboostmcr() clf.fit(X, y) y_hat = clf.predict(X) print(y_hat)
参考资料:
- https://blog.csdn.net/sai_simon/article/details/123751406?spm=1001.2014.3001.5506
- https://blog.csdn.net/sai_simon/article/details/123751454?spm=1001.2014.3001.5506
- https://zhuanlan.zhihu.com/p/602345835
- Hastie T , Rosset S , Zhu J ,et al.Multi-class AdaBoost[J].International Press of Boston, 2009(3).DOI:10.4310/SII.2009.V2.N3.A8.
t_proba.dtype).eps, None, out=y_predict_proba)