递归详解之青蛙跳台阶和汉诺塔问题
!!‧✧̣̥̇‧✦‧✧̣̥̇‧✦ ‧✧̣̥̇:Solitary-walk
⸝⋆ ━━━┓
- 个性标签 - :来于“云”的“羽球人”。 Talk is cheap. Show me the code
┗━━━━━━━ ➴ ⷯ本人座右铭 : 欲达高峰,必忍其痛;欲戴王冠,必承其重。
自
信
希望在看完我的此篇博客后可以对你有帮助哟此外,希望各位大佬们在看完后,可以互赞互关一下,看到必回
————————————————
版权声明:本文为CSDN博主「Solitary-walk」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/X_do_myself/article/details/134220644
一:递归的简单了解
1.递归定义:
递归的思想是把一个大型复杂问题层层转化为一个与原问题规模更小的问题,问题被拆解成子问题后,递归调用继续进行,直到子问题无需进一步递归就可以解决的地步为止。
换言之就是大事化小,小事化了的一个过程
2.递归的必要条件:
1)必须有递归结束的条件
2)在递归的过程中不断接近递归结束的条件
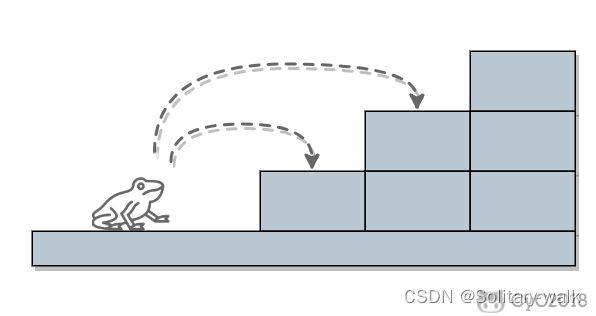
二:青蛙跳台阶
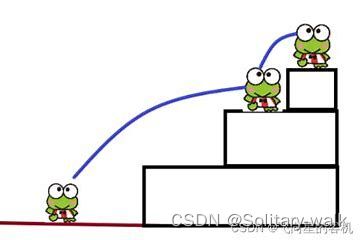
1.问题:从前有一只小青蛙,他想通过自己的实力来到台阶的最顶端,看看高处的放进如何,但是他遇到一个问题,不知道自己要如何走到顶峰,那么聪明的你,没错,就是此时正在玩博客的你,是否可以设计出青蛙跳台阶的这个过程?
接下来我们一起分析:
首先以3个台阶为例,进行分析:
其实大的角度无非就两个问题: 一次跳两个 ? 一次跳一个 进行组合
1) 一次跳一个
2) 先跳一个台阶 -> 再跳2个台阶
3) 先跳2个台阶 -> 再跳1给台阶
其实回归问题本质就是:
对于 n 个台阶,当第一次选择跳一个台阶的时候,剩余n-1 台阶要如何走
当第一次选择跳2个台阶的时候,剩余 n-2台阶如何走
ok ,想必有了以上的开胃小菜,接下来的代码实现就会很好理解
首先我们建立一个函数Jump(int n) : 表示跳n 个台阶有多少种方法
Jump(n) = Jump(n-1) + Jump(n-2) 借助递归算法很简便
int Jump(int n)
{
//n = 1,只有一种跳法
// n = 2 ,2种跳法
if (n == 1)
{
return 1;
}
if (n == 2)
{
return 2;
}
if (n > 2)
{
return Jump(n - 1) + Jump(n - 2);
}
}优化之后的代码
int Jump(int n)
{
/*if (n == 1)
{
return 1;
}
if (n == 2)
{
return 2;
}*/
if (n <= 2)
{
return n;
}
if (n > 2)
{
return Jump(n - 1) + Jump(n - 2);
}
}三:汉诺塔问题
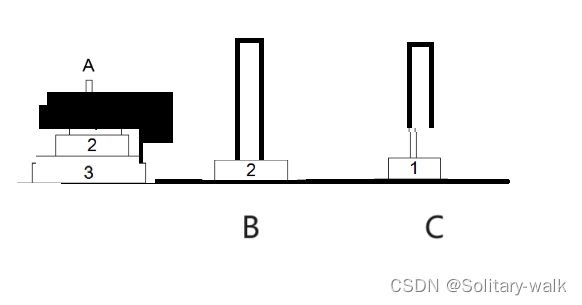
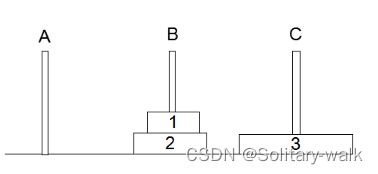
问题的描述是:有三根柱子,A、B、C,A柱上放有n个大小不等的圆盘,大的在下,小的在上。要求把A柱上的圆盘全部移到C柱上,并且在移动过程中要遵守以下规则:一次只能移动一个圆盘;大的圆盘不能放在小的圆盘上面。
接下来咱话不多,直接进行分析就行:
初状态的草图:
这里我们需要借助C柱子,把1,2号盘子移动到我的B柱子上
草图如下:
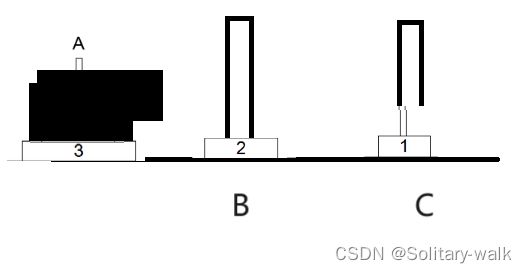
1)盘子1的移动:
2)盘子2:
3)盘子3:
4)
1)盘子1的移动: A->C
2 ) 盘子2 :A->B
3) 盘子3 :需要先把盘子2移动到B上 C->B 接着是移动盘子3 A->C
4)1移动到A,B->A
5)2移动到C ,B->c
6) 1直接移动到C ,A->C
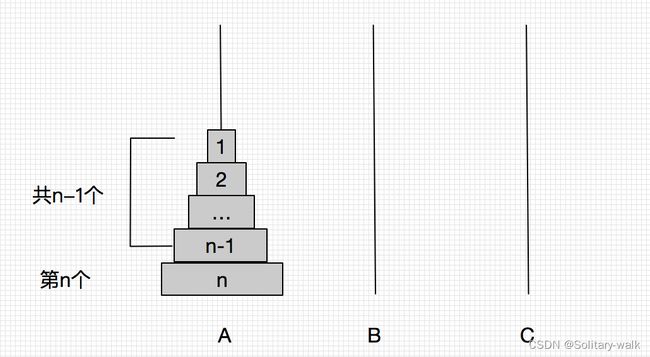
接下来回归问题本质:
对于n个盘子而言就是 前n-1个盘子的移动和第n个盘子的移动
在这里我设计2个函数
Hanoi(int n,char pos1,char poos2,char pos3) 用来递归实现移动
Move(char pos1,char pos2) 用来打印盘子的移动过程
void Hanoi(int n, char pos1, char pos2, char pos3) //此函数用来递归实现盘子的移动,移动的本质就是:起始位置->中转位置->目标位置
{
//注意: pos1;盘子的起始位置,A pos2:中转位置,B pos3:盘子最终的目标位置,C
// n:盘子的个数
//当是一个盘子的话,直接从我的起始位置移动到我的目标位置
if (n == 1)
{
Move(pos1, pos3);
}
else
{
//当n>1其实就是一个就是 n-1个盘子和一个盘子的移动问题
Hanoi(n - 1, pos1, pos3, pos2);//注意这里的第二个参数表示盘子的中转位置,并不表示我的目标位置
Move(pos1, pos3);//A柱子上的最后一个盘子直接移动到我的目标位置
Hanoi(n - 1, pos2, pos1, pos3);
}
}
}
int main()
{
Hanoi(2, 'A', 'B', 'C');
printf("\n");
Hanoi(3, 'A', 'B', 'C');
printf("\n");
return 0;
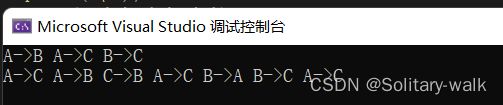
}运行结果:
以上就是我今日的share,递归这个思想是很重要的在后期的学习中我也会不断更新,各位大佬们,觉得还不错的话,互关互赞一下吧,蟹蟹