树与图的搜索

目录

树与图的深度优先遍历

树与图的宽度优先遍历

---

树与图的深度优先遍历

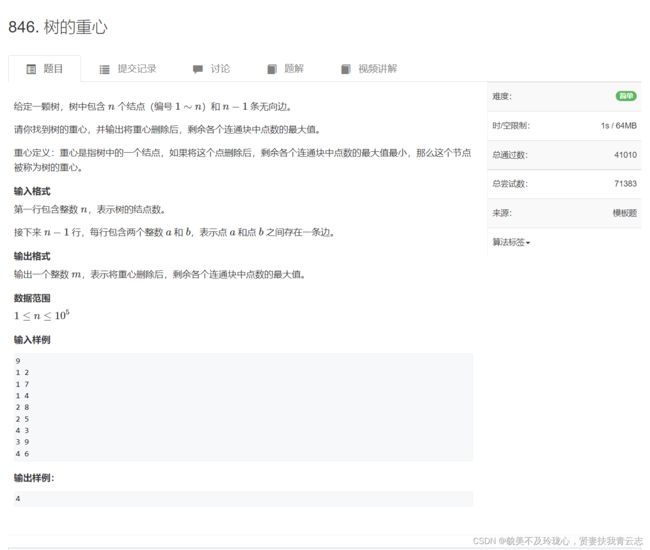
题目如下：

树是一种特殊的图，是一种无环连通图，图分两种，无向图（边无方向）和有向图（边有方向），无向图可以看成是一种特殊的有向图（建一条双向边），所以树是一种特殊的图。常用邻接表来存储。邻接表就是本质单链表，邻接矩阵也可以存储数和图。

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

分析

在实际写算法的是否不需要一致记着它的意义，我们只需要背下这个模板即可，直接套用

这个临界表存储是图，表示点与点存在边，可以再加一个属性表示边与边的距离

深度优先遍历 —— 模板

dfs(int u)//搜索所有与u相连的节点
{
	修改状态
	for(遍历邻接表搜索)
	{
		当前点未被搜索过，递归搜索该节点
	}
	return;
}

无向图邻接表存储

idx其意义可以认为是节点，也表示边的数目

M=2*N；
int h[N],e[M],ne[M],idx;

void add(int a, int b)  
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
一个链条存储的是所有与a相连接的节点

解题代码

#include 
#include 

using namespace std;

const int N = 100010, M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int ans = N;
bool st[N];

// 三个数组模拟单链表结构，这个链条上都是和a相连的点
void add(int a, int b)  
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}


int dfs(int u)
{
    st[u] = true;

    int size = 0, sum = 1;
    for (int i = h[u]; i != -1; i = ne[i]) //遍历与u节点相连接的所有点
    {
        int j = e[i];
        if (st[j]) continue;
        int s = dfs(j);
        size = max(size, s);
        sum += s;
    }

    size = max(size, n - sum);
    ans = min(ans, size);

    return sum;
}

int main()
{
    scanf("%d", &n);

    memset(h, -1, sizeof h);

    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a); //无向图存储两条边
    }

    dfs(1);

    printf("%d\n", ans);

    return 0;
}

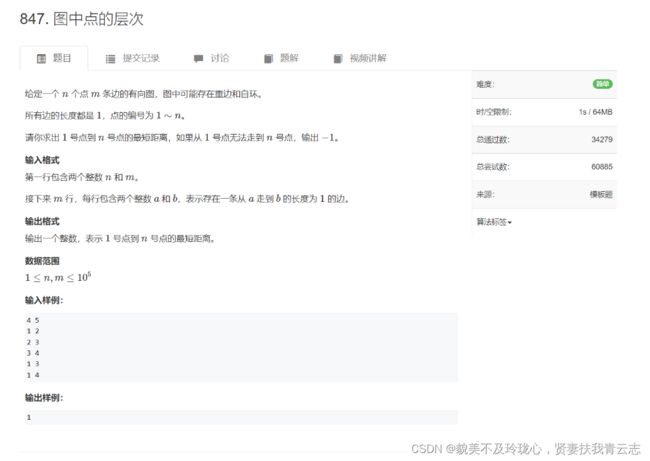
树与图的宽度优先遍历

重边：两个点之间有多条边 自环：一条边自己指向自己

BFS有个特点，它是按宽度，也就是层去搜索一个图，所以比较适合解决最短路问题。

bfs思路

bfs()
{
	queue<> q;//队列存储节点的编号
	while(q.size())
	{
		for(迭代与节点相连接的所有点)
		{
			点未被遍历到，就更新距离，放入队列。
		}
	}
}

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int bfs()
{
    memset(d, -1, sizeof d);

    queue q;
    d[1] = 0;
    q.push(1);

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (d[j] == -1)
            {
                d[j] = d[t] + 1;
                q.push(j);
            }
        }
    }

    return d[n];
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    cout << bfs() << endl;

    return 0;
}

宽度搜索的思路：依次取出队头的元素，进行搜索宽度搜索，while循环控制深度的层数，队列中存储的是一层中的所有的点。