基于python的BP神经网络

该程序的功能是实现三层BP神经网络；
其中输入层有三个神经元，隐藏层有四个神经元，输出层有三个神经元；
程序的目的是随机生成一个（3,1）的矩阵，然后定义标签为（0,1,0），通过前向传导和反向传导，最终输出的结果接近标签值。
生成的数据用X表示
两层权重参数分别用W1，W2表示
两层偏置参数分别用b1,b2表示
隐藏层节点的输入为layer1,输出为layer1_out
输出层节点的输入为layer2,输出为layer2_out

import numpy as np
import random
import matplotlib.pyplot as plt

###生成数据
X=np.random.randn(3,1)
target=np.array([[0],
                 [1],
                 [0]])
#生成权重参数
W1=np.random.rand(4,3)
b1=np.random.rand(4,1)
W2=np.random.rand(3,4)
b2=np.random.rand(3,1)


def layer(W,data,b):
    out=np.dot(W,data)+b
    return out

def sigmoid(x):
    s=1/(1+np.exp(-x))
    return s
# def backsigmoid(y):
#     s=1/(1+np.exp(-y))
#     s=s*(1-s)
#     return s
#损失函数，均方误差
def mean_squared_error(m,n):
    return 0.5*np.sum((m-n)**2)

epoch1=[]

if __name__ == "__main__":
     #学习率leaningrate
    loss1=[]
    leaningrate=0.1   
    epoch=0
    for i in range (100):
        #前向传到
        layer1=layer(W1,X,b1)
        layer1_out=sigmoid(layer1)
        layer2=layer(W2,layer1_out,b2)
        layer2_out=sigmoid(layer2)
        
        #计算损失函数
        loss=mean_squared_error(layer2_out,target)
        loss1.append(loss)
        epoch=epoch+1
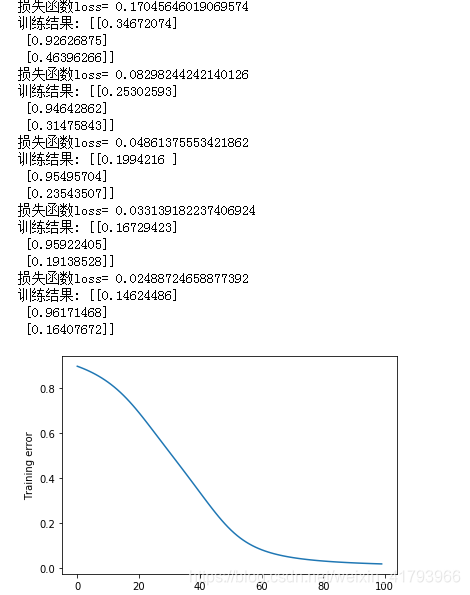
        if i%10==0:
            print("损失函数loss=",loss)
            print("训练结果:",layer2_out)
        #反向传导
        pianW2=np.dot(np.dot(np.dot((layer2_out-target),layer2_out.T),(1-layer2_out)),layer1_out.T)
        #注意上一步和下一步的矩阵有些需要转置，需要计算一下矩阵的维度做出判断
        W2=W2-leaningrate*pianW2
        pianW1=np.dot((np.dot(np.dot(np.dot(np.dot(np.dot((layer2_out-target).T,layer2_out),(1-layer2_out).T),W2),layer1_out),(1-layer1_out).T)).T,X.T)
        W1=W1-leaningrate*pianW1
        
        
    plt.plot(loss1)
    plt.xlabel('Number of epochs')
    plt.ylabel('Training error')
    #最终的训练结果值是不固定的，因为每次训练都会生成新的输入和权重

实验结果

附录给出了关于反向传导的推导链接 https://zhuanlan.zhihu.com/p/24801814
下图是本程序的反向推导过程草稿，以备需要时复习
代码优化，主要的改变是定义了一个类

import numpy as np
import random
import matplotlib.pyplot as plt


class BP():
    def __init__(self,inputnum=5,hiddennum=6,outputnum=5,learning_rate=0.002):
        self.inputnum=inputnum
        self.hiddennum=hiddennum
        self.outputnum=outputnum
        self.learning_rate=learning_rate
    def generatedata(self):
        X=np.random.randn(self.inputnum,1)
        W1=np.random.rand(self.hiddennum,self.inputnum)
        b1=np.random.rand(self.hiddennum,1)
        W2=np.random.rand(self.outputnum,self.hiddennum)
        b2=np.random.rand(self.outputnum,1)
        target=np.array([[1],[0],[1],[1],[0]])
        return X,W1,b1,W2,b2,target
    def layer(self,W,data,b):
        out=np.dot(W,data)+b
        return out
    
    def sigmoid(self,x):
        s=1/(1+np.exp(-x))
        return s
    
    def mean_squared_error(self,m,n):
        return 0.5*np.sum((m-n)**2)
    
    def train(self):
        X,W1,b1,W2,b2,target=self.generatedata()
        loss1=[]
        epoch=0
        for i in range (2000):
        #前向传到
            layer1=self.layer(W1,X,b1)
            layer1_out=self.sigmoid(layer1)
            layer2=self.layer(W2,layer1_out,b2)
            layer2_out=self.sigmoid(layer2)
            
            #计算损失函数
            loss=self.mean_squared_error(layer2_out,target)
            loss1.append(loss)
            epoch=epoch+1
            if i%10==0:
                print("损失函数loss=",loss)
                print("训练结果:",layer2_out)
            #反向传导
            pianW2=np.dot(np.dot(np.dot((layer2_out-target),layer2_out.T),(1-layer2_out)),layer1_out.T)
            #注意上一步和下一步的矩阵有些需要转置，需要计算一下矩阵的维度做出判断
            W2=W2-self.learning_rate*pianW2
            pianW1=np.dot((np.dot(np.dot(np.dot(np.dot(np.dot((layer2_out-target).T,layer2_out),(1-layer2_out).T),W2),layer1_out),(1-layer1_out).T)).T,X.T)
            W1=W1-self.learning_rate*pianW1
        
        return loss1

if __name__ == "__main__":
    bp=BP()
    bp.train()
    loss1=bp.train()
    plt.plot(loss1)
    plt.xlabel('epochs')
    plt.ylabel('loss')