多边形的填充算法的分析
多边形的填充
分析
思路一
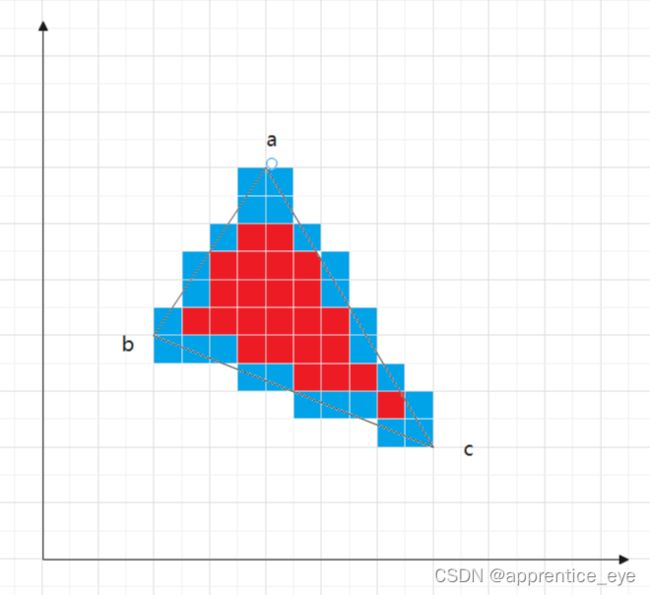
我们之前已经实现了对直线的扫描转换,但是现在我们遇到了新的问题那就是如何对多边形进行填充,如图所示,如何对图示的多边形进行填充呢?

我所想到的第一个办法是这样的,那就是假设上顶点为a,左顶点为b,右顶点为c,图示可以变成下面的图:

其中ab边,bc边,cd边所在的直线就分别可以使用下面的式子进行表示:
a b 边: A 1 ∗ x + B 1 ∗ y + C 1 = 0 ab边:A_1*x + B_1*y + C_1=0 ab边:A1∗x+B1∗y+C1=0
b c 边: A 2 ∗ x + B 2 ∗ y + C 2 = 0 bc边:A_2*x + B_2*y + C_2=0 bc边:A2∗x+B2∗y+C2=0
c a 边: A 3 ∗ x + B 3 ∗ y + C 3 = 0 ca边:A_3*x + B_3*y + C_3=0 ca边:A3∗x+B3∗y+C3=0
对于这三条边我们可以进行划分:
上边的两个点决定的边叫做上边,下边的两个点决定的边叫做下边,然后右边的两个点决定的边叫做右边。
如果一个点在三角形内,必然要满足此点在上边之下,下边之上,右边之左。也就是说将此点代入三个直线方程,上边的直线方程值小于0,右边的直线方程的值小于0,下边的直线方程的值大于0.
如图所示:
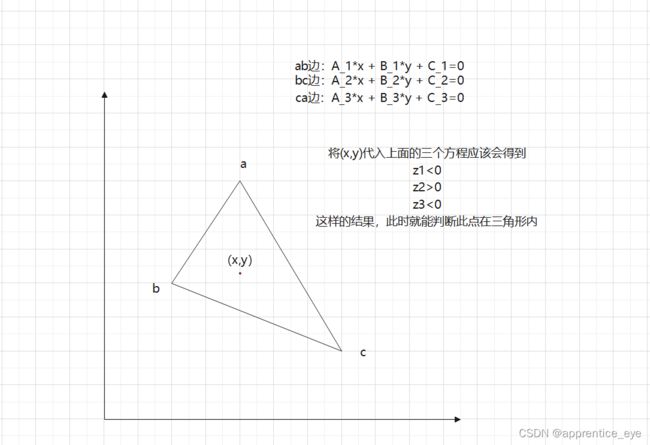
但是现在的方法有个弊端,他要求多个直线方程,还要判断点与直线之间的关系,在填充三角形的时侯我们还可以判断点与直线的关系,但当是四边形或五边形等更复杂的图形时就不适用了,为此我们需要寻求更好的算法。
思路二
现在既然求直线然后通过判断点与直线间满足的关系这种方法失败了,那么我们能不能构想一个更好的方法呢?
我们知道在点阵表示多边形时,由于是使用多边形内部的像素来刻画多边形的,所以必须得像素的中心处于多边形的内部,才能将此像素用于多边形的表示但是这一种表示损失了如顶点、几何边界等重要的信息。
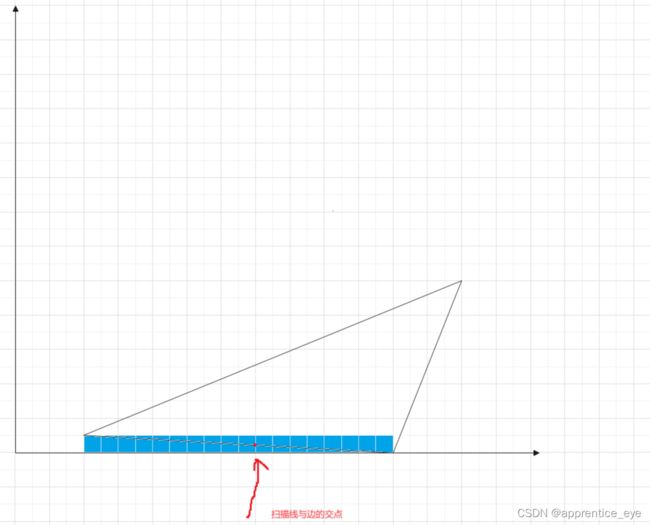
我们可以看到在一行之中绘制在多边形内的像素一定在假设有x轴与边界的交点用红色表示出来:
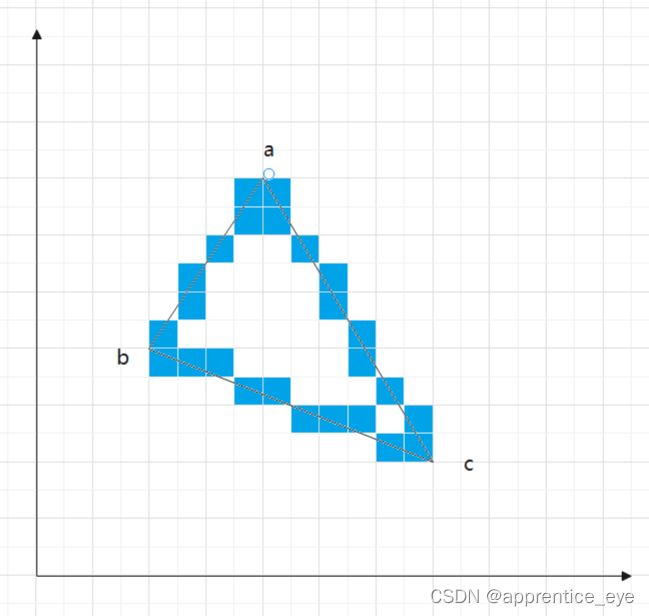
红色区域所表示的就是多边形的内部区域。
由此我们就能发现多边形内部的点的表示规则了。我们只看一行
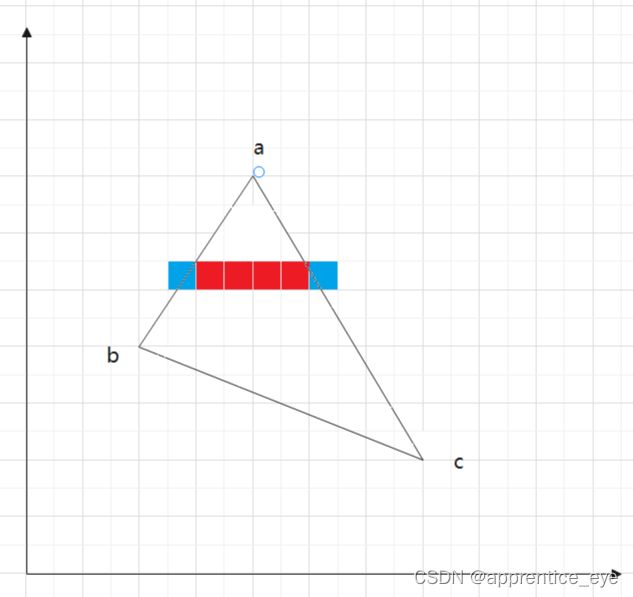
发现多边形内部的点就是由取定一个y值,然后再由此y值得到对应边的交点,在交点之间的像素就是应该绘制的像素点。
由于由y=c确定的一条直线是平行于x轴的直线,所以此方法又叫做x-扫描线法。
那么此规则对于边数超过3的多边形还适用吗?
如下图所示:
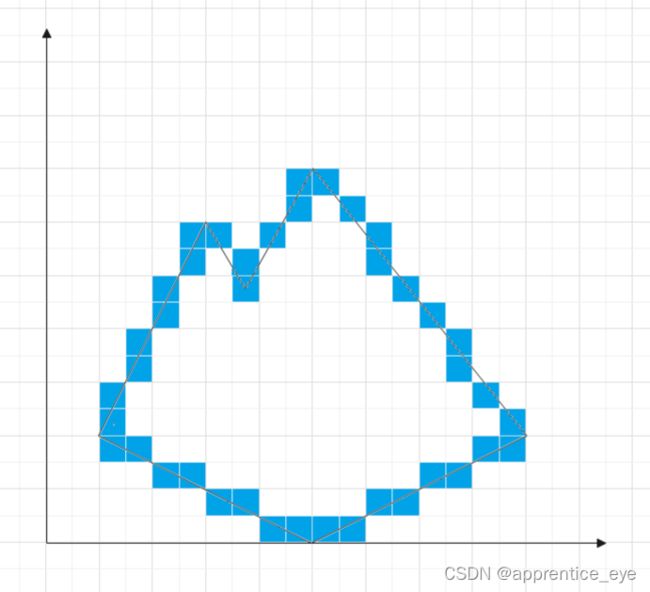
别的行都是两两左右进行配对这一行由于中间两条边的交点重合了变成了三个点,但是此时仍要进行两两配对,所以我们是不是可以定义一个数组,然后求边界的像素,对于边界像素,以其y值作为数组的下标(将y值做一个变换,使其可以作为数组的下标)由此,在同一行的两个边界点一定是在二维数组的同一行,因为我们将y值作为作为与数组下标有关的量,同时因为每一条边都从起点求到终点,所以当起点与终点重合时也会记录,所以就不用担心有边界点重合的问题了。
但是我们看图会发现新的问题,那就是:
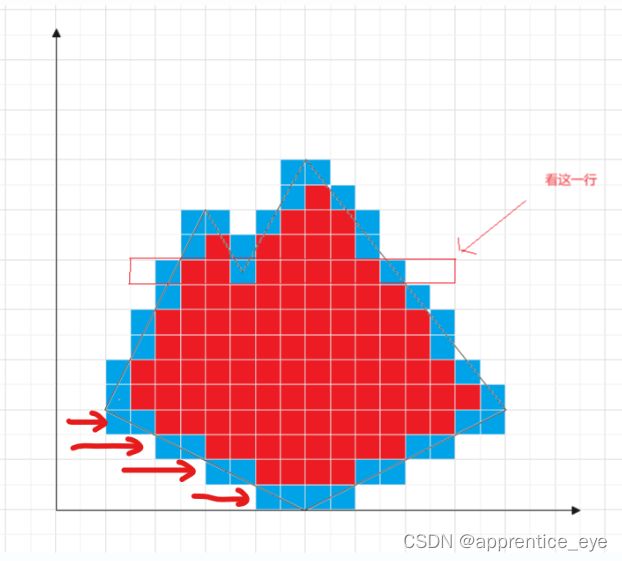
箭头所指的这几行,按理来说在求出边界点的时候会求出两个,但是边界我们是只需要一个的,所以这里我们是需要进行处理的。
此点后续再讨论
至此我们已经得出了x-扫描线法的所有分析,但是这一个算法我们是感觉有点差劲的,所以我们能不能得到更加高效的算法呢?
已知边界->种子填充法
我们现在已经知道多边形的边界了,在边界内部的点一定是属于多变形的点,而且在多边形内部的点的相邻的点一定属于多边形内部的点或者多边形的边,如下图所示:
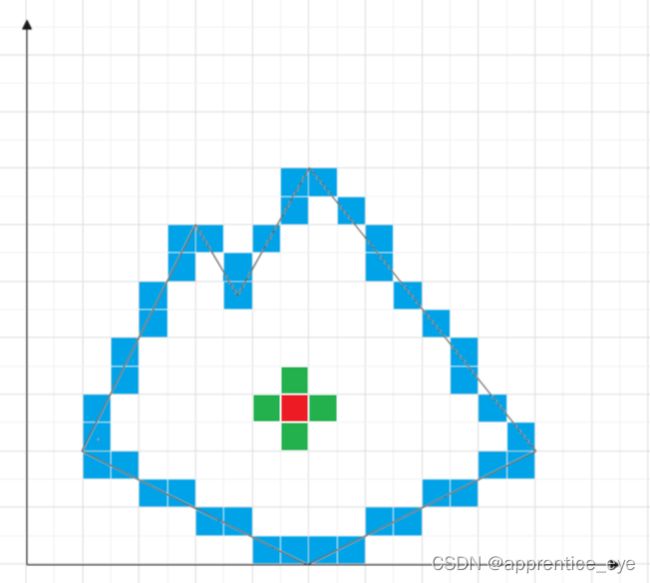
图中红色的点属于多边形,与红色点相邻的绿色点(4-邻域)也属于多边形,绿色点的邻接点也属于多边形以此类推,我们就能遍历多边形的内部,这样我们就能将多边形绘制出来。
这种就叫做种子填充法,我们知道我们填充一个像素点时接下来要填充的就是它的四个邻接点,然后是邻接点的临接点,一次类推,这类似于队列的结构,当然也可以使用栈这种数据结构来实现,这取决于个人喜好。
但是我们现在要抉择的是,是在像素点入队的时候进行像素点的绘制,还是在出队的时候进行像素点的绘制,我们简单分析一下就会得出,大致每出队一个元素就将入队四个元素,入队数大于出队数,很有可能将已经入队的元素再次入队,如果我们不在入队的时候进行像素点的绘制,我们就会因为无法判断对应像素点的是否已经绘制过而将其再次入队。
经过上面的分析,我们对于种子填充发已经有了十足的了解:
可以写出代码如下:
struct Queue {
int index_x;
int index_y;
struct Queue* next;
};
void Ctest3Dlg::OnBnClickedButton4() // 种子填充法进行多边形的绘制
{
// TODO: 在此添加控件通知处理程序代码
char* flag = (char*)malloc(sizeof(char) * 800 * 800);
for (int i = 0; i < 800 * 800; i++) {
flag[i] = 0;
}
auto startTime = std::chrono::high_resolution_clock::now();
CString str;
for (int i = 1; i < count; i++) {
CDC* pDC = GetDC();
paintLine(p[i - 1], p[i], pDC, flag); // 确定边界
ReleaseDC(pDC);
}
CDC* pDC = GetDC();
paintLine(p[count - 1], p[0], pDC, flag); // 确定边界
struct Queue* head = (struct Queue*)malloc(sizeof(struct Queue));
head->next = (struct Queue*)malloc(sizeof(struct Queue));
struct Queue* front, * rear;
front = head;
rear = front->next;
rear->next = NULL;
int mark = 0;
for (int i = down+1; i <= up; i++) { //寻找一个合适的种子
mark = 0;
for (int j = left+1; j <= right; j++) {
if (flag[i * 800 + j]) {
mark = 1;
}
else {
if (mark&&flag[i*800+j]==0) {
head->index_x = i;
head->index_y = j;
mark += 1;
}
}
if (mark == 2) {
break;
}
}
if (mark == 2) {
break;
}
}
CPoint paint;
paint.x = head->index_x;
paint.y = head->index_y;
pDC->SetPixelV(paint, RGB(255, 0, 0));
while (front != rear) {
int xx = front->index_x;
int yy = front->index_y;
front = front->next;
free(head);
head = front;
if (flag[(xx - 1) * 800 + yy] == 0) {
rear->index_x = xx - 1;
rear->index_y = yy;
CPoint paint;
paint.x = rear->index_y;
paint.y = rear->index_x;
rear->next = (struct Queue*)malloc(sizeof(struct Queue));
rear = rear->next;
rear->next = NULL;
pDC->SetPixelV(paint, RGB(255, 0, 0));
flag[(xx - 1) * 800 + yy] = 1;
}
if (flag[(xx + 1) * 800 + yy] == 0) {
rear->index_x = xx + 1;
rear->index_y = yy;
CPoint paint;
paint.x = rear->index_y;
paint.y = rear->index_x;
rear->next = (struct Queue*)malloc(sizeof(struct Queue));
rear = rear->next;
rear->next = NULL;
pDC->SetPixelV(paint, RGB(255, 0, 0));
flag[(xx + 1) * 800 + yy] = 1;
}
if (flag[xx * 800 + yy + 1] == 0) {
rear->index_x = xx;
rear->index_y = yy + 1;
CPoint paint;
paint.x = rear->index_y;
paint.y = rear->index_x;
rear->next = (struct Queue*)malloc(sizeof(struct Queue));
rear = rear->next;
rear->next = NULL;
pDC->SetPixelV(paint, RGB(255, 0, 0));
flag[xx * 800 + yy + 1] = 1;
}
if (flag[xx * 800 + yy - 1] == 0) {
rear->index_x = xx;
rear->index_y = yy - 1;
CPoint paint;
paint.x = rear->index_y;
paint.y = rear->index_x;
rear->next = (struct Queue*)malloc(sizeof(struct Queue));
rear = rear->next;
rear->next = NULL;
pDC->SetPixelV(paint, RGB(255, 0, 0));
flag[xx * 800 + yy - 1] = 1;
}
}
auto endTime = std::chrono::high_resolution_clock::now();
std::chrono::duration<double, std::milli> duration = endTime - startTime;
str.Format(_T("%lf"), duration.count());
time2.SetWindowText(str);
ReleaseDC(pDC);
}
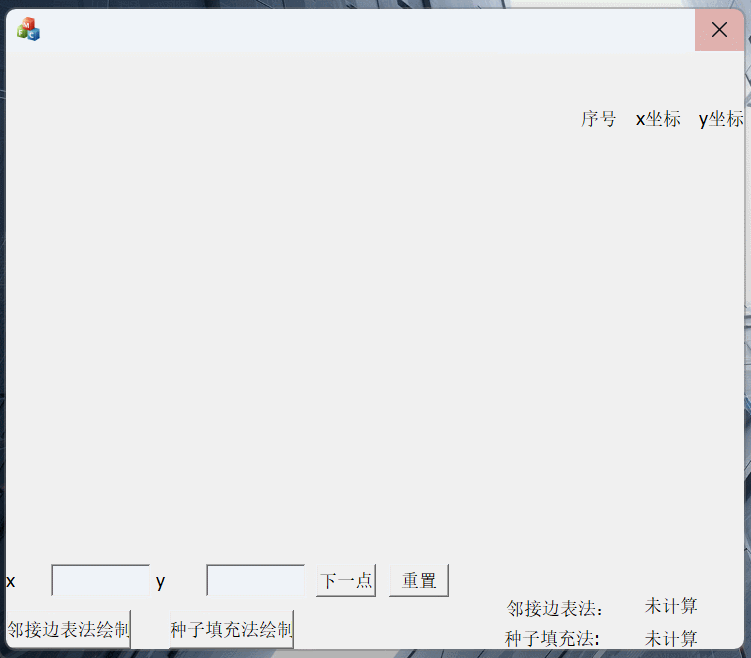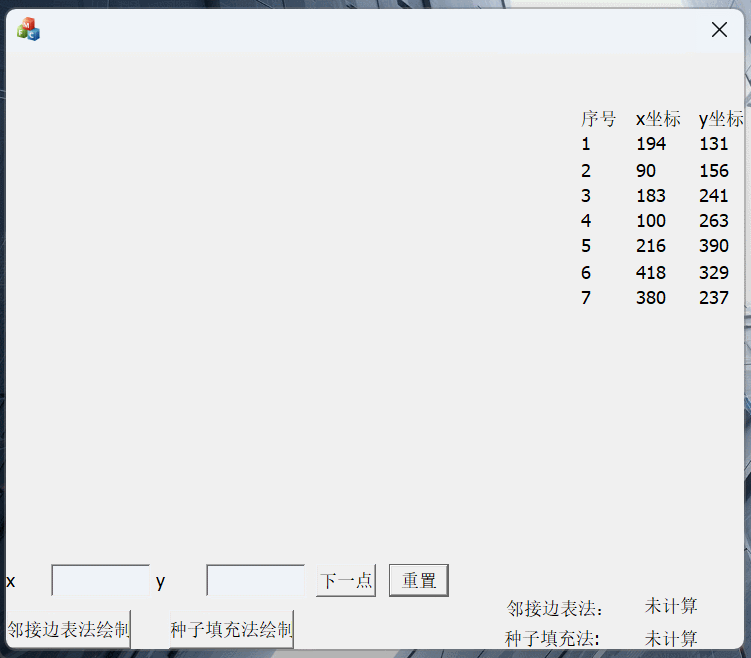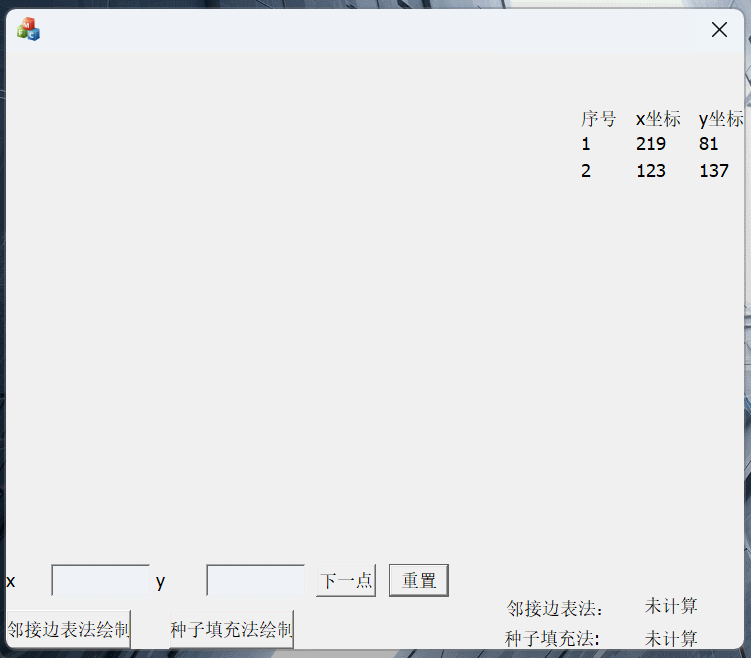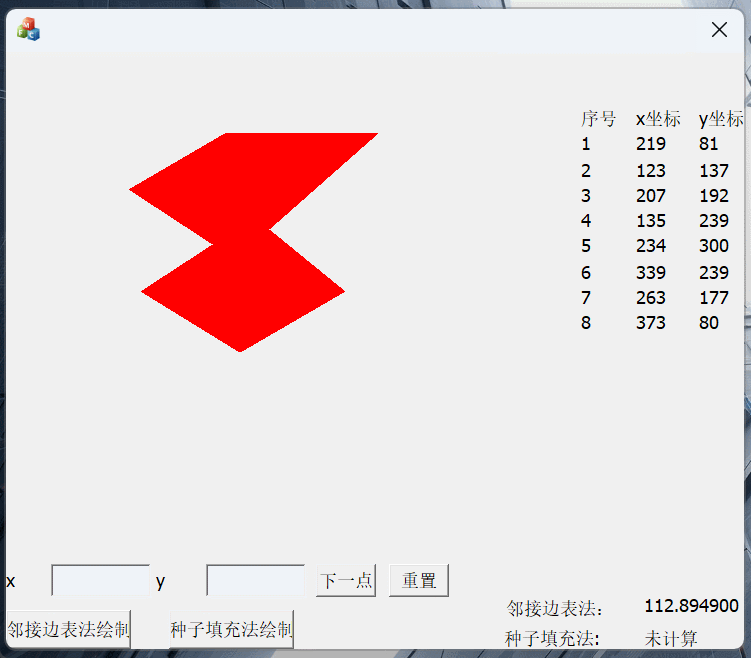
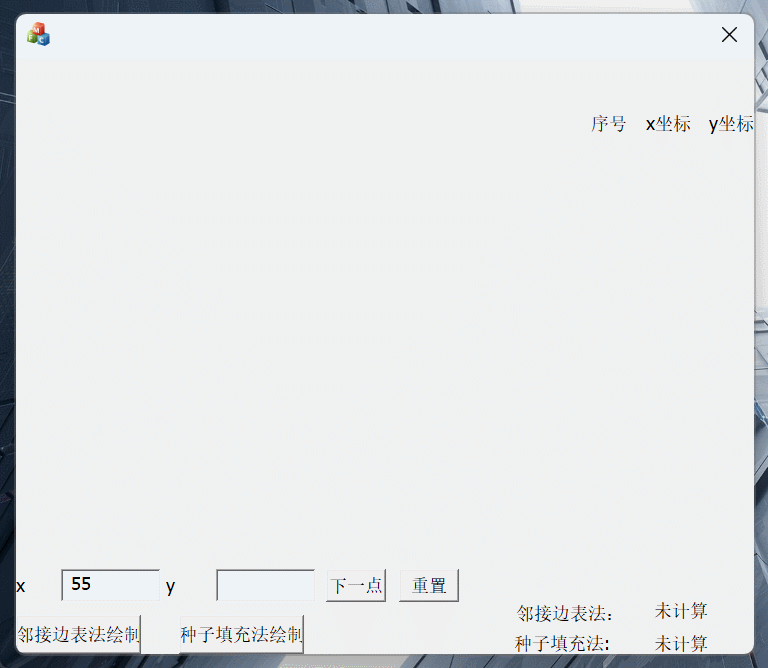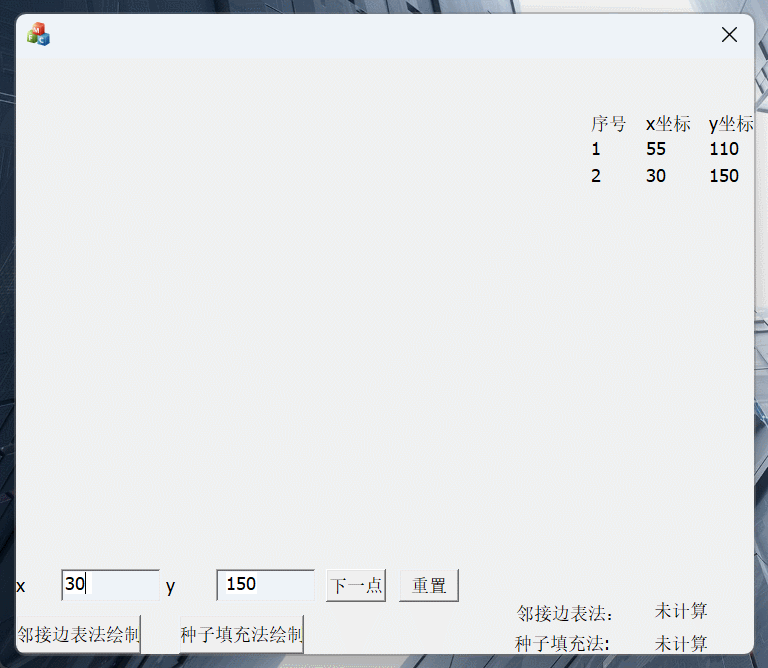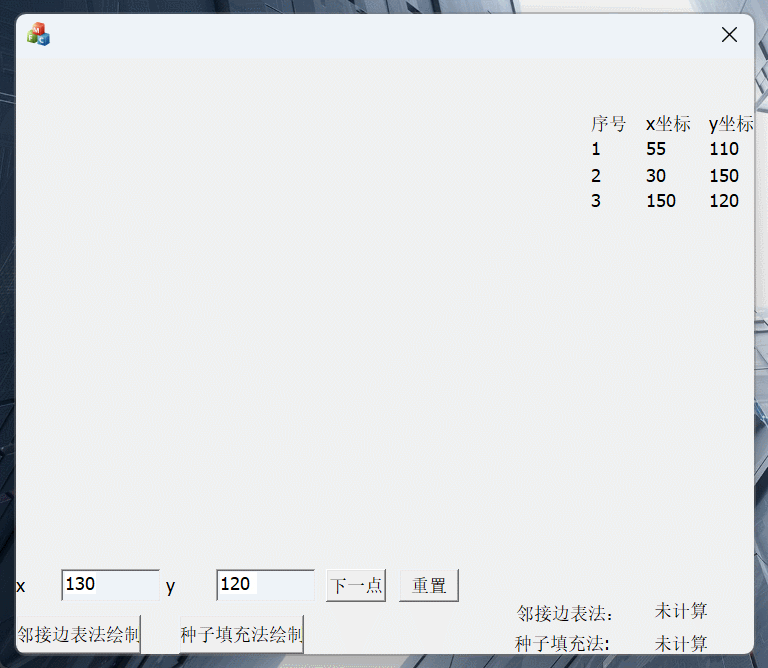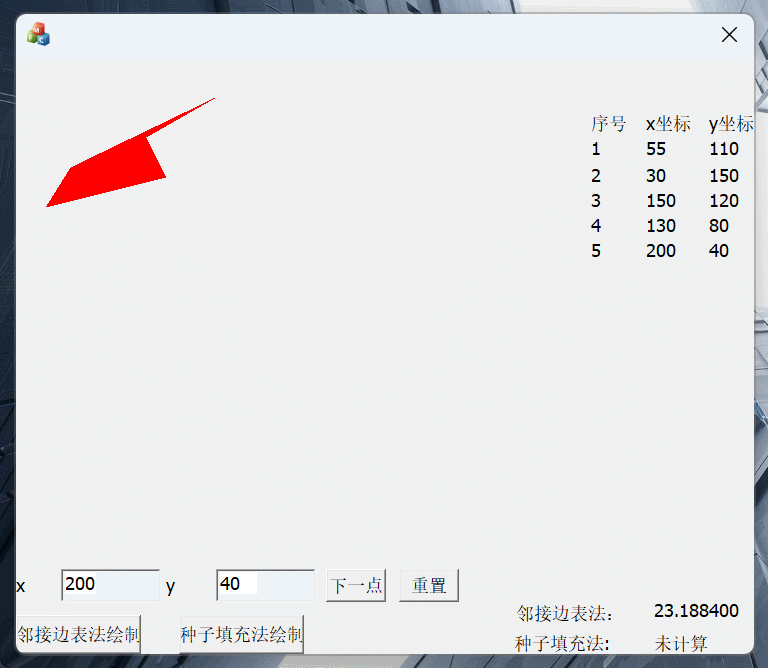
运行结果截图:
鼠标取点绘制:(注意我在绘制多边形的时候先绘制了多边形的边界,这样做的原因有两个:一是为了让整个多边形生成的时候有一个好的演示效果,在种子填充法中边界点是不需要绘制的, 二是在求边界的时候绘制很方便,在边表法中我们是边求交边绘制,如果要事先绘制边界就不太方便)
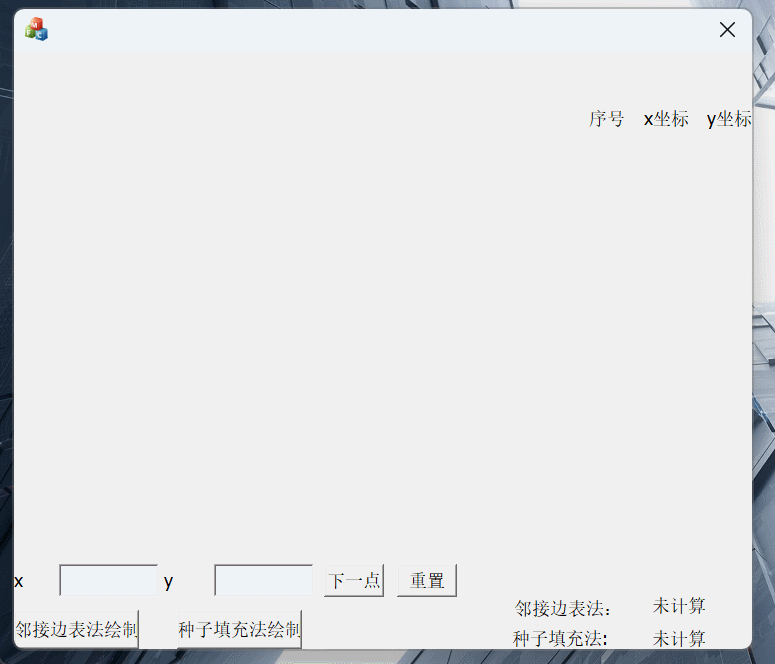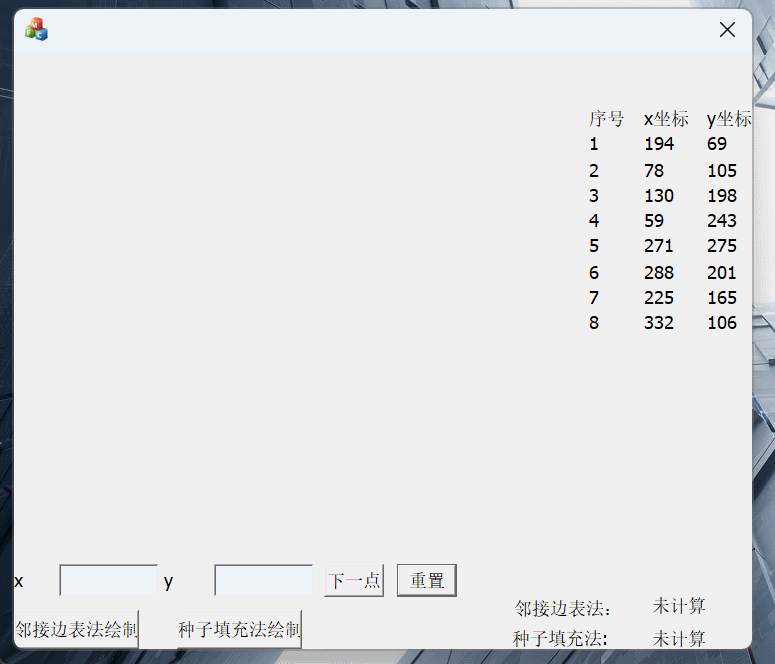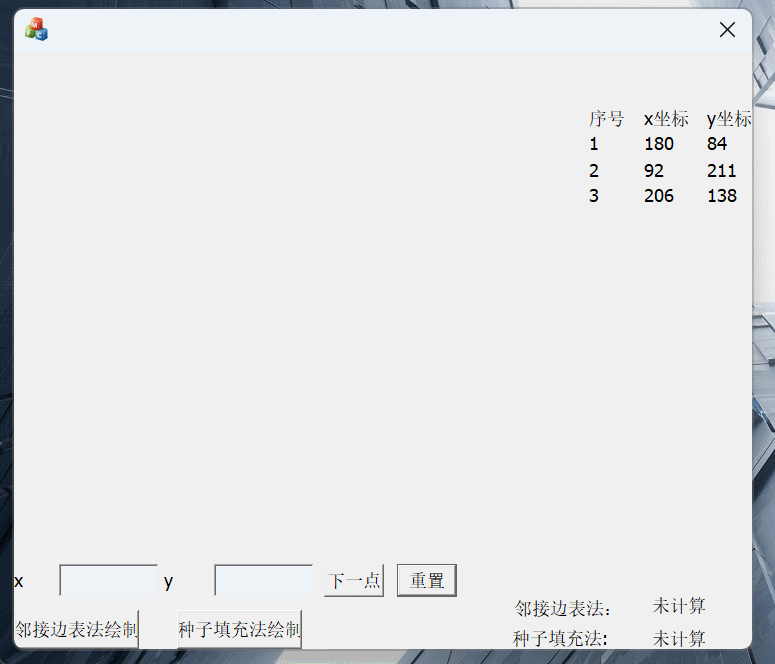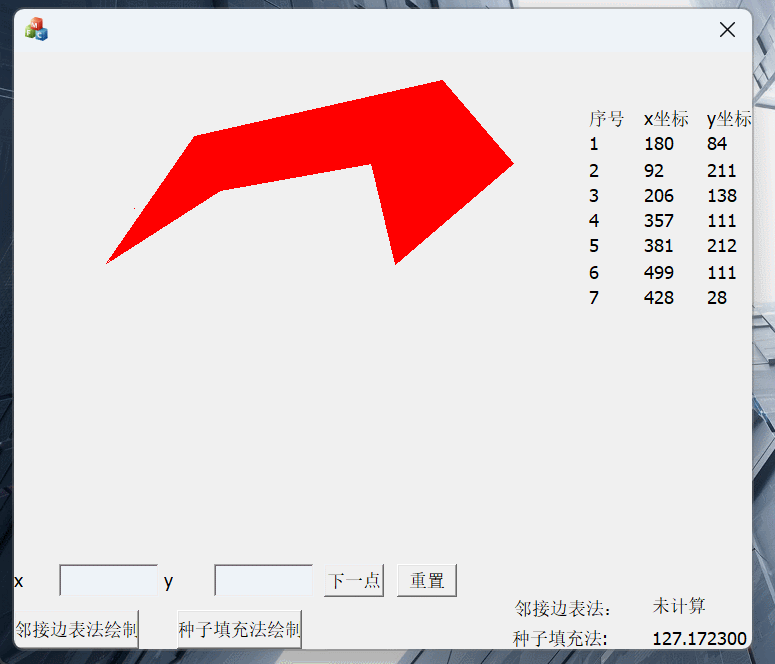
x-扫描线法
通过上面的分析我们已经知道如果先进行直线的扫描转换再进行求交就可能会造成交于一条直线同一点的两个位置,从而在两两配对时左边界无法与右边界进行配对从而导致中间的部分扫描不到,但是这种问题我们要如何进行解决呢?
我们可以在扫描边界时对边界做一个取舍,这样我们就能唯一选中一个点作为边界,但是这一种方法可能会造成图形的走样,如下:

对于下面这一个图形如果选择最右侧作为边界就会造成多边形多出一些像素,如果选择最右边的点作为边界又会少一些像素,为此我们可以对这一些像素做一个取中处理,这样我们就能得到一个较为合适的像素点作为边界点。
同样的我们可以使用下面的方法进行取边界点,我们此时不是从边的像素点中取边界点而是采用先使用x-扫描线与边进行相交,然后得到一个坐标值,对坐标值进行取整得到一个像素点的位置,使用此位置作为多边形的绘制边界,此时我们可以论证这种取法,与我们上面的在一系列边界点取中得到的结果是相同的。
按照取中法应该在下面两个像素中选择一个像素点作为边界:

我们可以看到点的左右两个像素,就是我们取中时位于中间的两个像素。
这是因为,在进行取中时,我们其实是在长边的二分之一处进行抉择,在扫描线相交时是在短边的二分之一处进行抉择,根据三角形的相似性,中间的点也是一样的,由此我们就能从上述方法中选择一种来进行执行。
根据上面的两种不同的边界点的选取策略我们可以写出不同的代码。
有效的邻接边表法
经过上述的x-扫描线法分析,我们已经能够求出每一行的x扫描线的边界点,但是此时仍然存在问题,那就是提前算出每一条线上的边界点时,那么我们能不能在绘制的过程中将每一行的边界点绘制出来然后在边界点之间填充像素点呢?答案是肯定的,我们来看一下下面的图示:
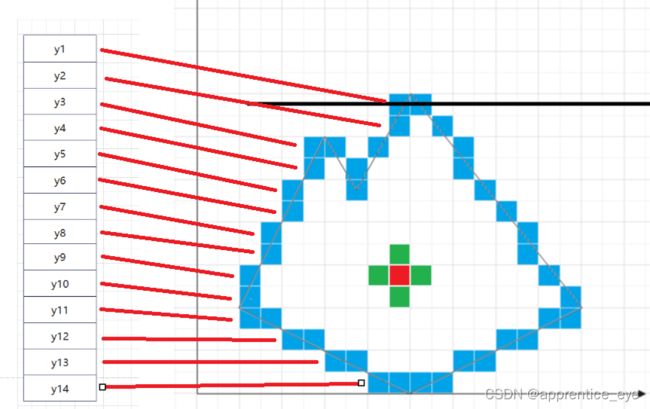
我们发现只需要在顶点的位置存储边的信息,比如上图的y1位置存储两条边的顶点信息,然后y2中的信息是可以由y1中的信息加上斜率来推导出来的,所以我们只需要再顶点部位存放点的信息。
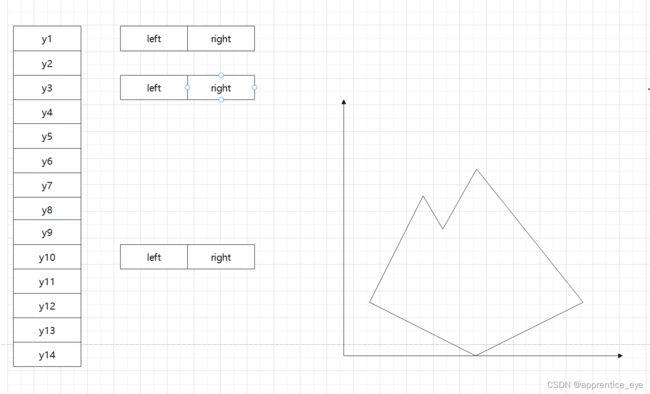
具体来说每一个结点需要我们存放什么信息呢?我们推导的前提是知道直线的增量对吧,所以结点中要放置增量,必须要有开始的位置,所以要放置起始点的坐标,因为y轴坐标是隐含的,所以只需要放置x的坐标就行了,同时我们也要放置直线结束的终点坐标,因为直线要结束,你不可能一直绘制下去。
故在边表的每一个节点中要放置以下三个数据。起始x数据, 增量数据, 终止y数据。
可以看出以此y值所在的平行于x轴的直线,这一点是两条边的顶点对吧,将y值下移,我们就可以得到发现相交的这两个点是上边顶点所在边的点,显然我们可以通过直线的扫描转换公式将这两个边界点确定下来,比如利用增量的DDA算法我们就可以知道当y变化1时x的变化量,依次递推我们就能在绘制的过程中依次确定边界点的位置。
大概如图所示的递推关系:

由y1求y2
接下来我们就分析,在同一行的两个坐标的我们可以按照x轴坐标递增的顺序安排整个边表的顺序,这样我们就能在配对的时候进行边界点的两两配对。
由此可以写出下述代码:
void Ctest3Dlg::OnBnClickedButton3()
{
// TODO: 在此添加控件通知处理程序代码
p[count] = p[0];
CDC* pDC = GetDC();
struct ListNode* list = (struct ListNode*)malloc(sizeof(struct ListNode) * 800);
for (int i = 0; i < 800; i++) {
list[i].next = NULL; // 对边表进行初始化
}
auto startTime = std::chrono::high_resolution_clock::now();
CString str;
for (int i = 0; i < count; i++) {
CPoint* updot = p[i].y > p[i + 1].y ? &p[i] : &p[i + 1]; // 添加对应的顶点到
CPoint* lowdot = p[i].y <= p[i + 1].y ? &p[i] : &p[i + 1];
struct ListNode* s = NULL;
int num = 0;
for (int j = 0; j < count; j++) {
s = &list[j];
while (s->next != NULL) {
s = s->next;
if (updot->y == s->data.end) {
num = 1;
break;
}
}
}
struct ListNode* p = &list[updot->y - num];
while (p->next != NULL) {
p = p->next;
}
p->next = (struct ListNode*)malloc(sizeof(struct ListNode));
p = p->next;
p->next = NULL;
p->data.start = updot->x;
p->data.end = lowdot->y;
p->data.increa = (updot->x - lowdot->x) * 1.0 / (updot->y - lowdot->y);
if (num) {
p->data.start = p->data.start - p->data.increa;
}
}
// 创建边表;
// 在创建的同时进行点的绘制
for (int i = up - 1; i > down; i--) {
struct ListNode* p = &list[i];
while (p->next != NULL) {
p = p->next;
}
struct ListNode* q = &list[i + 1];
while (q->next != NULL) {
q = q->next;
if (q->data.end < i) {
p->next = (struct ListNode*)malloc(sizeof(struct ListNode));
p = p->next;
p->next = NULL;
p->data.start = q->data.start - q->data.increa;
p->data.end = q->data.end;
p->data.increa = q->data.increa;
}
}
p = list[i].next;
q = list[i].next->next;
sort(list[i].next);
while (q != p) {
for (int j = p->data.start; j < q->data.start; j++) {
CPoint paint;
paint.x = j;
paint.y = i;
pDC->SetPixelV(paint, RGB(255, 0, 0));
}
if (q->next == NULL) {
p = NULL;
q = NULL;
}
else {
p = p->next->next;
q = q->next->next;
}
}
}
ReleaseDC(pDC);
auto endTime = std::chrono::high_resolution_clock::now();
std::chrono::duration duration = endTime - startTime;
str.Format(_T("%lf"), duration.count());
time1.SetWindowText(str);
}