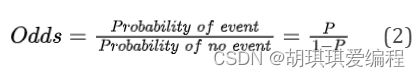MNL——多项Logit模型学习笔记（一）离散选择以及logit模型介绍

效用最大化准则：多项Logit模型（MNL）——离散选择模型之十四 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/112887273

↑资料来源，都是按照这里面的内容整理的，我只是整理一下自己学习用

1、离散选择模型

1.1 离散选择模型简介

DCM，Discrete Choice Model，即离散选择模型，DCM的常见模型有很多，包括二项Logit/Probit、多项Logit（MNL）、嵌套式Logit、有序Logit/Probit、混合Logit。所以在介绍MNL模型之前，先来介绍这个大类。

离散选择模型（Discrete Choice Model, DCM）在经济学领域和社会学领域都有广泛的应用。这种模型是指因变量不是连续的变量，例如，在交通安全研究领域，通常将交通事故的严重程度划分为3大类：（1）仅财产损失（Property Damage Only, PDO），（2）受伤（Injury），（3）死亡（Fatality）。在研究各类因素（如道路坡度、弯道曲率等、车龄、光照、天气条件等）对事故严重程度的影响的时候，由于因变量（事故严重程度）是一个离散变量（仅3个选项），使用离散选择模型可以提供一个有效的建模途径。

1.2 离散选择模型的相关要素

本文主要介绍离散选择模型的基本概念。一次选择行为通常会包含以下几种要素：

（1）决策者（Decision Makers），即做出选择行为的主体；

需要说明的是，决策者自身的属性也会对选择的结果产生影响。换句话说，即使面对相同的备选方案集，不同的决策者也会做出不一样的选择。这也是为什么在调查、收集用户/消费者的选择行为的数据时需要收集受访者的个人社会经济状况等资料的原因。常见的个体经济属性包括受访者的年龄、性别、收入、工作类型等等。很多销售公司利用他们所收集到的客户的资料，结合自身产品的特性，就可以制定出更加个性化的销售策略。

（2）备选方案集（Alternatives），通常会有多个方案供决策者选择（如决策者在考虑去哪里吃饭时，可能会考虑餐厅甲、餐厅乙、餐厅丙3个选项）；

所谓的备选方案就是供决策者选择的一个选择集。以交通出行方式的选择为例，可供人们选择出行方式一般有：常规公交、快速公交（BRT）、地铁、小汽车、出租车、合乘、自行车、电动自行车、以及步行等等。但是在实际情况中，针对不同的个体，其实际所面临的选择域可能并不一致。

因此，这里实际上涉及到3个不同的选择集的概念：

• 通用方案集（UniversalChoice Set）

• 可行方案集（FeasibleChoice Set）

• 实际考虑的方案集（ConsiderationChoice Set）

（3）各个方案的属性（Attributes of Alternatives）。例如在选择餐厅时，我们可能会考虑到餐厅的服务质量、价格高低、距离远近、环境是否优雅等多重因素。这里，每一种考虑因素称之为一个属性（Attribute）；

选择结果的除了受到决策者的个人属性的影响以外，每一选择项（即“方案”）的自身属性也会影响到选择的结果。这一点很容易理解。在出行方式选择的案例中，选择的结果除了受到出行者的个人属性（收入、工作类型等）的因素影响以外，人们在选择的时候还会考虑每一种出行方式的不同方面的属性特征，包括每一种出行方式的费用（Cost）、时间（Travel Time）、舒适性（Comfort）、安全性（Safety）、可靠性（Reliability）等等。可以说，正是各种方案在不同属性上的差异，才给决策者提供了一个选择的空间。

不同的方案属性描述了各方案提供给人们的不同维度上的效用（Utility）。“效用”是经济学中最常用的概念之一。百度百科中对“效用”的解释是：“它（效用）描述了消费者通过消费或者享受闲暇等使自己的需求、欲望等得到的满足的一个度量”

在这个例子中，出行费用越低，效用越高（满意度越高）；出行的舒适性越高，效用也越高（满意度越高），人们在进行选择的时候考虑的是各个方案在所有的属性维度上的总和——“效用最大化”也是最为常见的决策准则。

在离散选择模型中，等号的左边为决策个体i选择方案j的概率，等号的右边通常为“决策者的个人属性”和“方案属性”的函数。基于此，离散选择模型可以抽象的表示为：

（4）决策准则（Decision Rules）。不同的决策者在做出方案选择时的行为准则不尽然相同。仍然以上面“选择餐厅”的例子予以说明：有人在选择餐厅时可能会比较的“随意”——随便挑一家即可；而有的人可能会综合利用各种信息资源（如“大众点评”App）做出一个对自己最为有利的选择。不一样的决策准则会导致不同的选择结果。

有许多常见的理性决策方式，本文只介绍其中一种，即效用最大化准则，即满意程度最大化，效用最大化理论是离散选择模型的基础。以上文内容举例如下：

1.3 离散选择模型的类型

 离散选择模型的划分有多种方法。根据备选方案集中备选方案的数量可以将离散选择模型分为二项选择模型（Binomial choicemodels）和多项选择模型（Multinomialchoice models）。

二项选择模型：指备选方案集中仅有两个选项，如{“是”，“否”}，{“买”，“不买”}，{“受伤”，“未受伤”}

多项选择模型：如购买车辆时选择{“品牌1”、“品牌2”、“品牌3”}；交通事故的严重等级{“仅财产损失”、“受伤”、“死亡”}

除此之外还有其他分类方式，如根据备选方案的特征分类以及有序无序分类等。

1.4 离散选择模型常用软件

常用的离散选择模型软件有NLOGIT、SAS、Stata、SPSS、MATLAB、Python等。

2.Logit模型

 2.1 Odds

在统计学里，概率（Probability）和Odds都是用来描述某件事情发生的可能性的。

Odds指的是事件发生的概率与事件不发生的概率之比

以掷色子问题举例，出现点数6的概率P=1/6，出现其它点数的概率1-P=5/6。根据式(2)可以得到掷出点数为6这一事件的Odds为（1/6）÷（5/6）=1/5.用更通俗的语言来解释就是：平均来看，掷出6点的成功的概率和失败的概率之比为1:5。和概率论中许多其它的概念一样，Odds也是在赌博中产生的一个概念。假设甲乙二人掷骰子对赌；若甲出1块钱赌掷到6点，乙需要投注5块钱才能保证公平。

2.2 ODDS于概率p之间的关系

也就是说，事件A的Odds 等于 事件A出现的次数 和 其它（非A）事件出现的次数 之比；相比之下，事件A的概率 等于 事件A出现的次数 与 所有事件的次数 之比。比如随机摸出一个球、颜色为红色的概率为3/5，其所对应的Odds为3:2。 

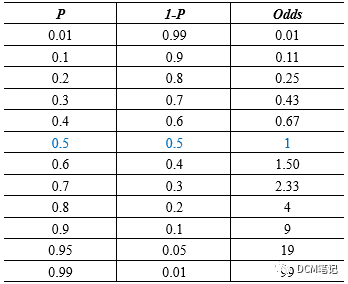
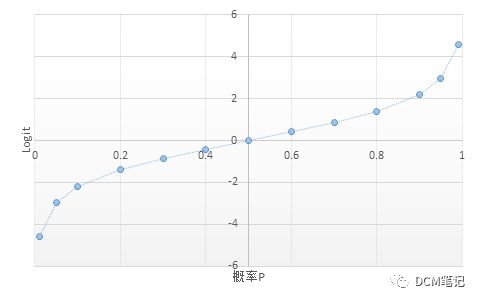
下图展示了P和Odds的变化规律：

从概率P→Odds→Logit， 这就是一个Logit变换。实际上，所谓 Logit 模型可以理解成 Log-it（即 it 的自然对数——这里的 it 指的就是Odds）。

 2.3 Logit的应用启发

 与概率不同，Logit的一个很重要的特性就是没有上下限——这就给建模带来极大方便。

线性模型 vs. Logistic模型——离散选择模型之二 (qq.com)

 在这篇文章中提到，不能直接使用线性回归模型：

 

3.何为Odds Ratio

上一节讲到了何为Odds，即事件A的Odds 等于事件A出现的次数和其它（非A）事件出现的次数之比，比如，对1000个样本进行观测，其中50个人为肺癌患者，而其余950人为健康者；那么观测到肺癌患者的Odds为：50/950

那么，什么什么是Odds Ratio？、

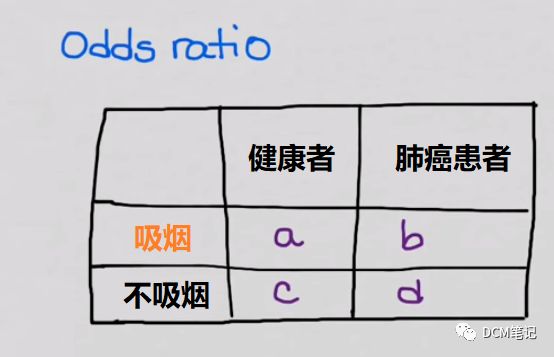
很显然，Odds Ratio（简称OR）指的是两个Odds的比值。继续上面的例子：研究人员怀疑是否患有肺癌和吸烟之间可能存在某种关系，于是按照“是否吸烟”和“是否患有肺癌”对样本进行进一步的划分，如下图1所示：

当OR>1时，分子上的Odds值较大——说明吸烟者得肺癌的几率（Odds）更高；若OR=1，则说明吸烟对是否患有肺癌没有影响。

OR是病例对照研究中经常用到的一个概念。百度了一下，OR有被翻译为“优势比”的，也有翻译成“比值比”的——个人更喜欢“优势比”，因为在我看来Odds实际上描述的是一种相对优势的概念。

4.summary

为了对MNL模型深入学习，本文介绍了一些基本概念作为知识储备。MNL模型作为离散选择模型的一种，本文首先介绍了何为离散选择模型、相关要素以及常用工具。其次本文针对Logit模型进行了介绍，为后面的学习打下基础。

后面的内容先回围绕这些相关因素进行展开，再引入二项Logit模型，最后才到多项Logit模型（MNL）。