第十五届蓝桥杯模拟赛(第二期)
第一题 计算 答案:108
std::cout<<36*30/10;第二题 快速幂 答案:608
#include
const int mod=1e3;
#define int long long
int qmi(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=(res*a)%mod;
b>>=1;
a=a*a%mod;
}
return res%mod;
}
signed main()
{
std::cout< 这题python一行输出语句就好了,但是c里面会溢出。
没学过快速幂就循环2023次就好了。
第三题 进制转换 答案:4169
#include
#define LL long long
int cnt;
int trans(int a,int x)//转成x进制
{
int sum=0;
while(a/x)
{
sum+=a%x;
a=a/x;
}
sum+=a;
return sum;
}
signed main()
{
for(int i=1;i<=10000000;i++)
{
if(trans(i,2)==trans(i,8))
{
cnt++;
std::cout< 第四题 约数个数 答案:901440
#include
#define LL long long
int a[]={393353,901440,123481,850930,423154,240461,
373746 ,232926, 396677, 486579 ,744860, 468782,941389,
777714, 992588, 343292, 385198 ,876426,483857, 241899,
544851, 647930, 772403, 109929,882745, 372491, 877710,
340000, 659788, 658675,296521, 491295, 609764, 718967,
842000, 670302};
signed main()
{
int maxn=-1;
int ans=0;
for(auto x:a)
{
int cnt=2;
for(int i=2;imaxn)
{
maxn=cnt;
ans=x;
}
}
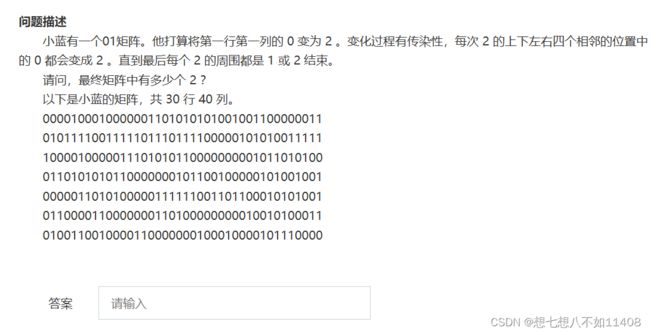
std::cout< 第五题 BFS 答案:541
#include
#define LL long long
const int N=50;
char g[N][N]={"0000100010000001101010101001001100000011",
"0101111001111101110111100000101010011111",
"1000010000011101010110000000001011010100",
"0110101010110000000101100100000101001001",
"0000011010100000111111001101100010101001",
"0110000110000000110100000000010010100011",
"0100110010000110000000100010000101110000",
"0010011010100110001111001101100110100010",
"1111000111101000001110010001001011101101",
"0011110100011000000001101001101110100001",
"0000000101011000010011111001010011011100",
"0000100000011001000100101000111011101100",
"0010110000001000001010100011000010100011",
"0110110000100011011010011010001101011011",
"0000100100000001010000101100000000000010",
"0011001000001000000010011001100101000110",
"1110101000011000000100011001001100111010",
"0000100100111000001101001000001010010001",
"0100010010000110100001100000110111110101",
"1000001001100010011001111101011001110001",
"0000000010100101000000111100110010101101",
"0010110101001100000100000010000010110011",
"0000011101001001000111011000100111010100",
"0010001100100000011000101011000000010101",
"1001111010010110011010101110000000101110",
"0110011101000010100001000101001001100010",
"1101000000010010011001000100110010000101",
"1001100010100010000100000101111111111100",
"1001011010101100001000000011000110110000",
"0011000100011000010111101000101110110001"};
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
int cnt;
typedef std::pair PII;
#define fir first
#define sec second
void bfs(int x,int y)
{
std::queue q;
q.push({x,y});
while(!q.empty())
{
auto t=q.front();
q.pop();
g[t.fir][t.sec]='2';
cnt++;
for(int i=0;i<4;i++)
{
int a=t.fir+dx[i],b=t.sec+dy[i];
if(a<0||b<0||a>29||b>39) continue;
if(g[a][b]!='0') continue;
g[a][b]='2';
q.push({a,b});
}
}
return ;
}
signed main()
{
bfs(0,0);
std::cout< 第六题 模拟
#include
#define LL long long
const int N=50;
signed main()
{
int n;
std::cin>>n;
std::string s=std::to_string(n);
s=s+s;
for(int i=1;i<7;i++)
std::cout< 第七题 模拟
#include
#define LL long long
const int N=50;
std::map mp;
signed main()
{
std::string s;
std::cin>>s;
mp['a']=mp['e']=mp['i']=mp['o']=mp['u']=1;
char ans;
for(int i=0;i 第八题 模拟
问题描述
给定一个整数,对这个整数的一次转换是指将这个整数变为这个整数的所有数位上的非零数字的乘积。
例如,对 123456789 进行一次转换变为 1*2*3*4*5*6*7*8*9=362880,再进行一次转换变为 3*6*2*8*8=2304,再进行一次转换变为 2*3*4=24,再进行一次转换变为 8。
给定一个整数,请依次将转换过程中经历的每个整数输出,直到小于 10 。输入格式
输入一行包含一个整数 n 。
输出格式
输出多行,每行包含一个整数。
样例输入
123456789
样例输出
362880
2304
24
8评测用例规模与约定
对于 50% 的评测用例,1 <= n <= 10**9 (10的9次方)。
对于所有评测用例,1 <= n <= 10**18 (10的18次方)。
我想复杂了,甚至不需要高精度,1e18 longlong就够了。
#include
#define int long long
const int N = 2e6 + 10;
int calc(std::string s)
{
int x=1;
for(int i=0;i>a;
while(a>10)
{
std::string s=std::to_string(a);
a=calc(s);
std::cout< 第九题 BFS
问题描述
小蓝站在一个 n 行 m 列的方格图中间,方格图的每一个方格上都标有一个正整数。
如果两个相邻方格(上下左右四个方向相邻)内的数的最大公约数大于 1 ,则可以从其中一个方格移动到另一个方格,当然也可以从另一个方格移回第一个方格。
假设小蓝开始时站在第 r 行第 c 列,请问小蓝可以移动到方格图内的多少个方格?输入格式
输入的第一行包含两个整数 n, m ,用一个空格分隔,表示方格图的行数和列数。
接下来 n 行,每行包含 m 个正整数,相邻整数间用一个空格分隔,依次表示方格图中从第 1 行到第 n 行,每行从第 1 列到第 m 列中的数。
接下来一行包含两个整数 r, c,用一个空格分隔,表示小蓝所在的行号和列号。输出格式
输出一行包含一个整数,表示答案。
样例输入
3 4
3 6 5 5
2 4 3 5
7 8 3 8
3 2样例输出
5
评测用例规模与约定
对于50%的评测用例,1 <= n, m <= 100,方格图中的每个数不超过 10**5 (10的5次方)。
对于所有评测用例,1 <= n, m <= 1000,方格图中的每个数不超过 10**9 (10的9次方)。
#include
const int N=1e3+10;
typedef std::pair PII;
#define fir first
#define sec second
int n,m;
int g[N][N];
int cnt;
bool st[N][N];
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
void bfs(int x,int y)
{
std::queue q;
q.push({x,y});
st[x][y]=true;
cnt++;
while(!q.empty())
{
auto t=q.front();
q.pop();
st[t.fir][t.sec]=true;
for(int i=0;i<4;i++)
{
int a=dx[i]+t.fir;
int b=dy[i]+t.sec;
if(st[a][b]) continue;
if(a<1||b<1||a>n||b>m) continue;
if(std::__gcd(g[a][b],g[t.fir][t.sec])<=1) continue;
st[a][b]=true;
cnt++;
q.push({a,b});
}
}
}
signed main()
{
std::cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) std::cin>>g[i][j];
}
int r,c;
std::cin>>r>>c;
bfs(r,c);
std::cout< 第十题 滑动窗口
问题描述
给定一个序列 a[1], a[2], …, a[n] 和一个整数 k,请找出一个长度正好为 k 的区间,使得区间中所有数的和最大。
即要找到一个整数 p ,使得 1 <= p 且 p+k-1 <= n ,使得 a[p]+a[p+1]+...+a[p+k-1] 最大。输入格式
输入的第一行包含两个整数 n , k。
第二行包含 n 个整数,相邻的整数之间使用一个空格分隔,表示给定的序列。输出格式
输出一行包含一个整数,表示最大的区间和,你只需要输出和就行,不需要输出方案。
样例输入
6 3
2 3 9 1 9 5样例输出
19
评测用例规模与约定
对于 30% 的评测用例,1 <= k <= n <= 30,1 <= a[i] <= 100。
对于 60% 的评测用例,1 <= k <= n <= 1000,1 <= a[i] <= 10000。
对于所有评测用例,1 <= k <= n <= 100000,1 <= a[i] <= 1000000。
要记得开long long
#include
const int N=100000+10;
typedef long long ll;
int n,k;
int a[N];
signed main()
{
std::cin>>n>>k;
for(int i=1;i<=n;i++) std::cin>>a[i];
ll maxn=-1e9;
ll sum=0;
for(int i=1;i<=n;i++)
{
sum+=a[i];
if(i>k) sum-=a[i-k];
maxn=std::max(maxn,sum);
}
std::cout< 出这期主要是因为好多人私信要,不得不说蓝桥杯的流量真大。
然后因为没有oj评测,只保证过样例,欢迎大佬指正。