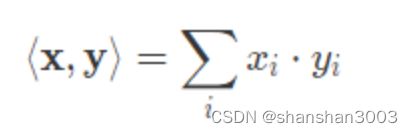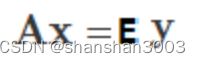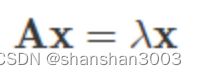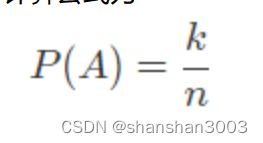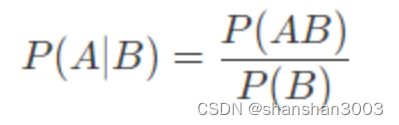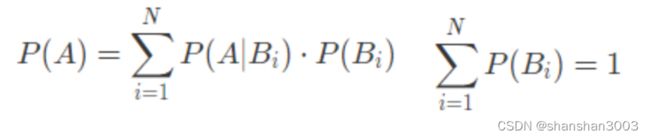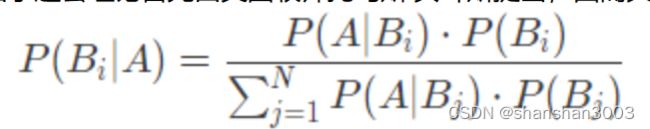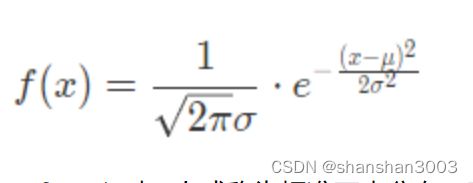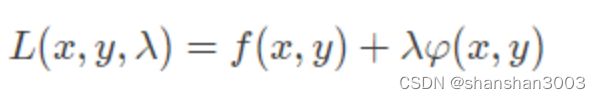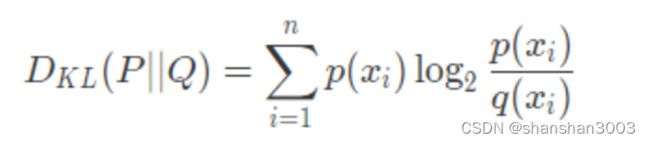人工智能基础课--数学基础

（1）人工智能基础课--数学基础

开篇词 (1讲)

开篇词 | 人工智能：新时代的必修课

普及人工智能的基础知识，走出了解人工智能的第一步。人工智能复杂，但并不神秘。它建立在以线性代数和概率论为骨架的基础数学上，通过简单模型的组合实现复杂功能。在工程上，深度神经网络通常以其恒河沙数般的参数让人望而却步；可在理论上，其数学原理却具有更好的可解释性。从事年薪百万的高端研究固然需要非凡的头脑，但理解人工智能的基本原理绝非普通人遥不可及的梦想。

专栏的内容将分为以下几个模块：

1. 数学基础。数学基础知识蕴含着处理智能问题的基本思想与方法，也是理解复杂算法的必备要素。这一模块我将介绍研究人工智能必备的数学基础知识，包括线性代数、概率论、最优化方法等。

2. 机器学习。机器学习的作用是从数据中习得学习算法，进而解决实际的应用问题，是人工智能的核心目标之一。这一模块我将介绍机器学习中的主要方法，包括线性回归、决策树、支持向量机、聚类等。

3. 人工神经网络。作为机器学习的一个分支，神经网络将认知科学引入机器学习当中，以模拟生物神经系统对真实世界的交互反映，并取得了良好的效果。这一模块我将介绍神经网络中的基本概念，包括多层神经网络、前馈与反向传播、自组织神经网络等。

4. 深度学习。简而言之，深度学习就是包含多个中间层的神经网络，数据的爆炸和计算力的飙升推动了深度学习的崛起。这一模块我将介绍深度学习的概念与实现，包括深度前馈网络、深度学习中的正则化、自动编码器等。

5. 神经网络实例。在深度学习框架下，一些神经网络已用于各种应用场景，并取得了不俗的效果。这一模块我将介绍几种神经网络实例，包括卷积神经网络、递归神经网络、深度信念网络等。

6. 深度学习之外的人工智能。深度学习既有优点也有局限，其他方向的人工智能研究正是有益的补充。这一模块我将介绍几种与深度学习无关的学习方法，包括马尔可夫随机场、迁移学习、集群智能等。

7. 应用实例。除了代替人类执行重复性的劳动之外，在诸多实际问题的处理中，人工智能也提供了有意义的尝试。这一模块我将介绍人工智能技术在几类实际任务中的应用，包括计算机视觉、语音识别、对话系统等。

数学基础 (7讲)

01 数学基础 | 九层之台，起于累土：线性代数

范数（norm）和内积（inner product）

范数（norm）是对单个向量大小的度量，描述的是向量自身的性质，其作用是将向量映射为一个非负的数值。通用的 Lp 范数定义如下：

对⼀个给定向量，L1 范数计算的是向量所有元素绝对值的和，L2 范数计算的是通常意义上的向量长度，L∞ 范数计算的则是向量中最大元素的取值。

内积（inner product）计算的则是两个向量之间的关系。两个相同维数向量内积的表达式为

内积能够表示两个向量之间的相对位置，即向量之间的夹角。一种特殊的情况是内积为 0，即 〈x,y〉=0。在二维空间上，这意味着两个向量的夹角为 90 度，即相互垂直。而在高维空间上，这种关系被称为正交（orthogonality）。如果两个向量正交，说明他们线性无关，相互独立，互不影响。

如果有一个集合，它的元素都是具有相同维数的向量（可以是有限个或无限个）， 并且定义了加法和数乘等结构化的运算，这样的集合就被称为线性空间（linear space），定义了内积运算的线性空间则被称为内积空间（inner product space）。在线性空间中，任意一个向量代表的都是 n 维空间中的一个点；反过来， 空间中的任意点也都可以唯一地用一个向量表示。两者相互等效。

参考系的选取

在线性空间上点和向量的相互映射中，一个关键问题是参考系的选取。

在内积空间中，一组两两正交的向量构成这个空间的正交基（orthogonal basis）。假若正交基中基向量的 L2 范数都是单位长度 1，这组正交基就是标准正交基（orthonormal basis）。正交基的作用就是给内积空间定义出经纬度。⼀旦描述内积空间的正交基确定了，向量和点之间的对应关系也就随之确定。

对二维空间来说，平面直角坐标系和极坐标系就对应了两组不同的正交基，也代表了两种实用的描述方式。

矩阵

矩阵可以表示向量的变化也可以描述参考系本身。

线性空间的一个重要特征是能够承载变化。当作为参考系的标准正交基确定后，空间中的点就可以用向量表示。当这个点从一个位置移动到另一个位置时，描述它的向量也会发生改变。点的变化对应着向量的线性变换（linear transformation），而描述对象变化抑或向量变换的数学语言，正是矩阵。

在线性空间中，变化的实现有两种方式：一是点本身的变化，二是参考系的变化。在第一种方式中，使某个点发生变化的方法是用代表变化的矩阵乘以代表对象的向量。可是反过来，如果保持点不变，而是换一种观察的角度，在这种情况下，矩阵的作用就是对正交基进行变换。因此，对于矩阵和向量的相乘，就存在不同的解读方式：

解读一：这个表达式既可以理解为向量 x 经过矩阵 A 所描述的变换，变成了向量 y；

解读二：也可以理解为一个对象在坐标系 A 的度量下得到的结果为向量 x，在标准坐标系 I（单位矩阵：主对角线元素为 1，其余元素为 0）的度量下得到的结果为向量 y。

即：

这表示矩阵不仅能够描述变化，也可以描述参考系本身。引用网络上一个精当的类比：表达式 Ax 就相当于对向量 x 做了一个环境声明，用于度量它的参考系是 A。如果想用其他的参考系做度量的话，就要重新声明。而对坐标系施加变换的方法，就是让表示原始坐标系的矩阵与表示变换的矩阵相乘。

矩阵的特征值（eigenvalue）和特征向量（eigenvector）

描述矩阵的⼀对重要参数是特征值（eigenvalue）和特征向量（eigenvector）。对于给定的矩阵 A，假设其特征值为λ，特征向量为 x，则它们之间的关系如下：

正如前文所述，矩阵代表了向量的变换，其效果通常是对原始向量同时施加方向变化和尺度变化。可对于有些特殊的向量，矩阵的作用只有尺度变化而没有方向变化，也就是只有伸缩的效果而没有旋转的效果。对于给定的矩阵来说，这类特殊的向量就是矩阵的特征向量，特征向量的尺度变化系数就是特征值。

矩阵特征值和特征向量的动态意义在于表示了变化的速度和方向。如果把矩阵所代表的变化看作奔跑的人，那么矩阵的特征值就代表了他奔跑的速度，特征向量代表了他奔跑的方向。

但矩阵可不是普通人，它是三头六臂的哪吒，他的不同分身以不同速度（特征值）在不同方向（特征向量）上奔跑，所有分身的运动叠加在⼀起才是矩阵的效果。

求解给定矩阵的特征值和特征向量的过程叫做特征值分解，但能够进行特征值分解的矩阵必须是 n 维方阵。将特征值分解算法推广到所有矩阵之上，就是更加通用的奇异值分解。

02 数学基础 | 月有阴晴圆缺，此事古难全：概率论

古典概率模型下事件概率

计算公式为

条件概率

可如果要刻画两个随机事件之间的关系，这个定义就不够看了。在一场足球比赛中，球队 1:0 取胜和在 0:2 落后的情况下 3:2 翻盘的概率显然是不一样的。这就需要引入条件概率的概念。

条件概率（conditional probability）是根据已有信息对样本空间进行调整后得到的新的概率分布。假定有两个随机事件 A 和 B，条件概率就是指事件 A 在事件 B 已经发生的条件下发生的概率，用以下公式表示

表示的是 A 和 B 两个事件共同发生的概率。如果联合概率等于两个事件各自概率的乘积，即 P(AB)=P(A)⋅P(B)

对于相互独立的事件，条件概率就是自身的概率，即 P(A∣B)=P(A)。

全概率

基于条件概率可以得出全概率公式（law of total probability）全概率公式的作用在于将复杂事件的概率求解转化为在不同情况下发生的简单事件的概率求和，即

逆概率

所谓“逆概率”解决的是在事件结果已经确定的条件下（P(A)），推断各种假设发生的可能性（P(Bi∣A)）

由于这套理论首先由英国牧师托马斯·贝叶斯提出，因而其通用的公式形式被称为贝叶斯公式：

上式：按照条件概率的公式：P(Bi|A)=P(BiA)/P(A)；

分子为条件概率P(BiA)，分母为全概率：P(A)

贝叶斯公式可以进一步抽象为贝叶斯定理（Bayes' theorem）：

式中的 P(H) 被称为先验概率（prior probability），即预先设定的假设成立的概率；

P(D∣H) 被称为似然概率（likelihood function），是在假设成立的前提下观测到结果的概率；

P(H∣D) 被称为后验概率（posterior probability），即在观测到结果的前提下假设成立的概率。

注：在D没发生的情况下，H发生的概率称之为先验概率。在获取D发生的概率信息之后，对于P(H|D)有了新的估计，被称之为后验概率。

从科学研究的方法论来看，贝叶斯定理提供了一种全新的逻辑。它根据观测结果寻找合理的假设，或者说根据观测数据寻找最佳的理论解释，其关注的焦点在于后验概率。概率论的贝叶斯学派（Bayesian probability）正是诞生于这种理念。

在贝叶斯学派眼中，概率描述的是随机事件的可信程度。如果手机里的天气预报应用给出明天下雨的概率是 85%，这就不能从频率的角度来解释了，而是意味着明天下雨这个事件的可信度是 85%。

频率学派和贝叶斯学派

频率学派认为假设是客观存在且不会改变的，即存在固定的先验分布，只是作为观察者的我们无从知晓。因而在计算具体事件的概率时，要先确定概率分布的类型和参数，以此为基础进行概率推演。

贝叶斯学派则认为固定的先验分布是不存在的，参数本身也是随机数。换言之，假设本身取决于观察结果，是不确定并且可以修正的。数据的作用就是对假设做出不断的修正，使观察者对概率的主观认识更加接近客观实际。

概率的估计有两种方法：最大似然估计法（maximum likelihood estimation）和最大后验概率法（maximum a posteriori estimation），两者分别体现出频率学派和贝叶斯学派对概率的理解方式。

最大似然估计法的思想是使训练数据出现的概率最大化，依此确定概率分布中的未知参数，估计出的概率分布也就最符合训练数据的分布。

最大后验概率法的思想则是根据训练数据和已知的其他条件，使未知参数出现的可能性最大化，并选取最可能的未知参数取值作为估计值。

在估计参数时，最大似然估计法只需要使用训练数据，最大后验概率法除了数据外还需要额外的信息，就是贝叶斯公式中的先验概率。

从理论的角度来说，频率学派和贝叶斯学派各有千秋，都发挥着不可替代的作用。但具体到人工智能这一应用领域，基于贝叶斯定理的各种方法与人类的认知机制吻合度更高，在机器学习等领域中也扮演着更加重要的角色。

描述随机变量（random variable）

概率论的一个重要应用是描述随机变量（random variable）。根据取值空间的不同，随机变量可以分成两类：离散型随机变量（discrete random variable）和连续型随机变量（continuous random variable）。在实际应用中，需要对随机变量的每个可能取值的概率进行描述。

离散变量的每个可能的取值都具有大于 0 的概率，取值和概率之间一一对应的关系就是离散型随机变量的分布律，也叫概率质量函数（probability mass function）。概率质量函数在连续型随机变量上的对应就是概率密度函数（probability density function）。

一些重要的概率分布

重要的离散分布包括两点分布、二项分布和泊松分布，重要的连续分布则包括均匀分布、指数分布和正态分布。

两点分布（Bernoulli distribution）：适用于随机试验的结果是二进制的情形，事件发生 / 不发生的概率分别为 p/(1−p)。任何只有两个结果的随机试验都可以用两点分布描述，抛掷一次硬币的结果就可以视为等概率的两点分布。

二项分布（Binomial distribution）：将满足参数为 p 的两点分布的随机试验独立重复 n 次，事件发生的次数即满足参数为 (n,p) 的二项分布。二项分布的表达式可以写成 P(X=k)=Ckn⋅pk⋅(1−p)(n−k),0≤k≤n。

泊松分布（Poisson distribution）：放射性物质在规定时间内释放出的粒子数所满足的分布，参数为 λ 的泊松分布表达式为 P(X=k)=λk⋅e−λ/(k!)。当二项分布中的 n 很大且 p 很小时，其概率值可以由参数为 λ=np 的泊松分布的概率值近似。

均匀分布（uniform distribution）：在区间 (a, b) 上满足均匀分布的连续型随机变量，其概率密度函数为 1 / (b - a)，这个变量落在区间 (a, b) 内任意等长度的子区间内的可能性是相同的。

指数分布（exponential distribution）：满足参数为 θ 指数分布的随机变量只能取正值，其概率密度函数为 e−x/θ/θ,x>0。指数分布的一个重要特征是无记忆性：即 P(X > s + t | X > s) = P(X > t)。

正态分布（normal distribution）：参数为正态分布的概率密度函数为

当 μ=0,σ=1 时，上式称为标准正态分布。正态分布是最常见最重要的一种分布，自然界中的很多现象都近似地服从正态分布。

常见的数字特征

除了概率质量函数 / 概率密度函数之外，另一类描述随机变量的参数是其数字特征。数字特征是用于刻画随机变量某些特性的常数，包括数学期望（expected value）、方差（variance）和协方差（covariance）。

数学期望和方差描述的都是单个随机变量的数字特征，如果要描述两个随机变量之间的相互关系，就需要用到协方差和相关系数。协方差度量了两个随机变量之间的线性相关性，即变量 Y 能否表示成以另一个变量 X 为自变量的 aX+b 的形式。

根据协方差可以进一步求出相关系数（correlation coefficient），相关系数是一个绝对值不大于 1 的常数，它等于 1 意味着两个随机变量满足完全正相关，等于 -1 意味着两者满足完全负相关，等于 0 则意味着两者不相关。需要说明的是，无论是协方差还是相关系数，刻画的都是线性相关的关系。如果随机变量之间的关系满足 Y=X2，这样的非线性相关性就超出了协方差的表达能力。

03 数学基础 | 窥一斑而知全豹：数理统计

数理统计（mathematical statistics）根据观察或实验得到的数据来研究随机现象，并对研究对象的客观规律做出合理的估计和判断。

用一句不严谨但直观的话讲：数理统计可以看成是逆向的概率论。用买彩票打个比方，概率论解决的是根据已知的摇奖规律判断一注号码中奖的可能性，数理统计解决的则是根据之前多次中奖 / 不中奖的号码记录以一定的精确性推测摇奖的规律，虽然这种尝试往往无功而返。

在数理统计中，可用的资源是有限的数据集合，这个有限数据集被称为样本（sample）。相应地，观察对象所有的可能取值被称为总体（population）。数理统计的任务就是根据样本推断总体的数字特征。样本通常由对总体进行多次独立的重复观测而得到，这保证了不同的样本值之间相互独立，并且都与总体具有相同的分布。

在统计推断中，应用的往往不是样本本身，而是被称为统计量的样本的函数。统计量本身是一个随机变量，是用来进行统计推断的工具。样本均值和样本方差是两个最重要的统计量：

统计推断的基本问题可以分为两大类：参数估计（estimation theory）和假设检验（hypothesis test）。

参数估计

参数估计是通过随机抽取的样本来估计总体分布的方法，又可以进一步划分为点估计（point estimation）和区间估计（interval estimation）。

参数估计--点估计

在已知总体分布函数形式，但未知其一个或者多个参数时，借助于总体的一个样本来估计未知参数的取值就是参数的点估计。点估计的核心在于构造合适的统计量 θ^，并用这个统计量的观察值作为未知参数 θ 的近似值。

点估计的具体方法包括矩估计法（method of moments）和最大似然估计法（maximum likelihood estimation）。

矩表示的是随机变量的分布特征，k 阶矩的定义为随机变量的 k 次方的均值，即 E(X^k)。

矩估计法的思想在于用样本的 k 阶矩估计总体的 k 阶矩，其理论依据（大数定理）在于样本矩的函数几乎处处收敛于总体矩的相应函数，这意味着当样本的容量足够大时，几乎每次都可以根据样本参数得到相应总体参数的近似值。

最大似然估计的直观理解是：既然抽样得到的是已有的样本值，就可以认为取到这一组样本值的概率较大，因而在估计参数 θ 的时候就需要让已有样本值出现的可能性最大。

注：一个同学和一个猎人去打猎，窜出一个兔子，一枪被打中，请问是谁打中的，因为猎人打中的概率大，所以认为是猎人打中的，这就是最大似然估计

在最大似然估计中，似然函数被定义为样本观测值出现的概率，确定未知参数的准则是让似然函数的取值最大化，也就是微积分中求解函数最大值的问题。由于不同的样本值之间相互独立，因而似然函数可以写成若干概率质量函数 / 概率密度函数相乘的形式，并进一步转化为对数方程求解。

在实际应用中，估计量的评价通常要考虑以下三个基本标准。

无偏性：估计量的数学期望等于未知参数的真实值；

有效性：无偏估计量的方差尽可能小；

一致性：当样本容量趋近于无穷时，估计量依概率收敛于未知参数的真实值。

参数估计--区间估计

对估计量的判别标准涉及了估计误差的影响，这是和估计值同样重要的参量。在估计未知参数 θ 的过程中，除了求出估计量，还需要估计出一个区间，并且确定这个区间包含 θ 真实值的可信程度。在数理统计中，这个区间被称为置信区间（confidence interval），这种估计方式则被称为区间估计。

置信区间可以用如下的方式直观解释：对总体反复抽样多次，每次得到容量相同的样本，则根据每一组样本值都可以确定出一个置信区间 (θ,θ)，其上界和下界是样本的两个统计量，分别代表了置信上限和置信下限。每个置信区间都存在两种可能性：包含 θ 的真实值或不包含 θ 的真实值。如果对所有置信区间中包含 θ 真实值的比率进行统计，得到的比值就是置信水平。因此，区间估计相当于在点估计的基础上进一步提供了取值范围和误差界限，分别对应着置信区间和置信水平。

假设检验

参数估计的对象是总体的某个参数，假设检验的对象则是关于总体的某个论断，即关于总体的假设。假设检验中的假设包含原假设 H0 和备择假设 H1；检验的过程就是根据样本在 H0 和 H1 之间选择一个接受的过程。

在数理统计中，发生概率小于 1% 的事件被称作小概率事件，在单次实验中被认为是不可能发生的。如果在一次观测得到的样本中出现了小概率事件，那么就有理由认为这不是真正意义上的小概率事件，原始的假设也就此被推翻。如果是备择假设被推翻，就意味着接受原假设；反之，如果是原假设被推翻，则意味着拒绝原假设。

从数理统计的角度看，监督学习算法的任务就是在假设空间中搜索能够针对特定问题做出良好预测的假设。学习器通过对测试数据集的学习得到具有普适性的模型，这个模型适用于不属于测试集的新样本的能力被称为泛化能力。显然，泛化能力越强，学习器就越好。

假设检验的作用就在于根据学习器在测试集上的性能推断其泛化能力的强弱，并确定所得结论的精确程度，可以进一步推广为比较不同学习器的性能。由于度量学习器性能的常用指标是错误率，假设检验中的假设就是对学习器的泛化错误率的推断，推断的依据就是在测试数据集上的测试错误率。具体的检验方式有很多种，在此不做赘述。

泛化误差

除了推断之外，对泛化性能的解释也是机器学习算法分析的重要内容。泛化误差的构成可以分为三部分：偏差（bias）、方差（variance）和噪声（noise）。

• 偏差表示算法预测值和真实结果之间的偏离程度，刻画的是模型的欠拟合特性；

• 方差表示数据的扰动对预测性能的影响，刻画的是模型的过拟合特性；

• 噪声表示在当前学习任务上能够达到的最小泛化误差，刻画的是任务本身的难度。

对任何实际的模型来说，偏差和方差都难以实现同时优化，反映出欠拟合与过拟合之间难以调和的矛盾。

04 数学基础 | 不畏浮云遮望眼：最优化方法

人工智能的目标就是最优化：在复杂环境与多体交互中做出最优决策。

最优化理论（optimization）研究的问题是判定给定目标函数的最大值（最小值）是否存在，并找到令目标函数取到最大值（最小值）的数值。如果把给定的目标函数看成连绵的山脉，最优化的过程就是判断顶峰的位置并找到到达顶峰路径的过程。

要实现最小化或最大化的函数被称为目标函数（objective function）或评价函数，大多数最优化问题都可以通过使目标函数 f(x) 最小化解决，最大化问题则可以通过最小化 −f(x) 实现。

根据约束条件的不同，最优化问题可以分为无约束优化（unconstrained optimization）和约束优化（constrained optimization）两类。

线性规划

线性规划（linear programming）就是一类典型的约束优化，其解决的问题通常是在有限的成本约束下取得最大的收益。约束优化问题通常比无约束优化问题更加复杂，但通过拉格朗日乘子（Lagrange multiplier）的引入可以将含有 n 个变量和 k 个约束条件的问题转化为含有 (n+k) 个变量的无约束优化问题。拉格朗日函数最简单的形式如下

式中 f(x,y) 为目标函数，φ(x,y) 则为等式约束条件，λ 是拉格朗日乘数。从数学意义上讲，由原目标函数和约束条件共同构成的拉格朗日函数与原目标函数具有共同的最优点集和共同的最优目标函数值，从而保证了最优解的不变性。

梯度下降法

求解无约束优化问题最常用的方法是梯度下降法（gradient descent）。梯度的方向是目标函数导数（derivative）的反方向。

当函数的输入为向量时，目标函数的图象就变成了高维空间上的曲面，这时的梯度就是垂直于曲面等高线并指向高度增加方向的向量，也就携带了高维空间中关于方向的信息。而要让目标函数以最快的速度下降，就需要让自变量在负梯度的方向上移动。这个结论翻译成数学语言就是“多元函数沿其负梯度方向下降最快”，这也是梯度下降法的理论依据。

在梯度下降算法中，另一个重要的影响因素是步长，也就是每次更新 f(x) 时 x 的变化值。较小的步长会导致收敛过程较慢，当 f(x) 接近最小值点时，步长太大反而会导致一步迈过最小值点，正所谓“过犹不及”。

以上是针对单个样本的梯度下降法，当可用的训练样本有多个时，样本的使用模式就分为两种。

一种是批处理模式（batch processing），即计算出在每个样本上目标函数的梯度，再将不同样本的梯度进行求和，求和的结果作为本次更新中目标函数的梯度。在批处理模式中，每次更新都要遍历训练集中所有的样本，因而运算量较大。

另一种模式叫做随机梯度下降法（stochastic gradient descent），它在每次更新中只使用一个样本，下一次更新再使用另外一个样本，在不断迭代的更新过程中实现对所有样本的遍历。有趣的是，事实表明当训练集的规模较大时，随机梯度下降法的性能更佳。

梯度下降法只用到了目标函数的一阶导数（first-order derivative），并没有使用二阶导数（second-order derivative）。

梯度下降法不能利用二阶导数包含的曲率信息，只能利用目标函数的局部性质，因而难免盲目的搜索中。已知目标函数可能在多个方向上都具有增加的导数，意味着下降的梯度具有多种选择。但不同选择的效果显然有好有坏。

遗憾的是，梯度下降法无法获知关于导数的变化信息，也就不知道应该探索导数长期为负的方向。由于不具备观察目标函数的全局视角，在使用中梯度下降法就会走出一些弯路，导致收敛速度变慢。而二阶导数所包含的全局信息能够为梯度下降的方向提供指导，进而获得更优的收敛性。

牛顿法（Newton's method）

如果将二阶导数引入优化过程，得到的典型方法就是牛顿法（Newton's method）。在牛顿法中，目标函数首先被泰勒展开，写成二阶近似的形式（相比之下，梯度下降法只保留了目标函数的一阶近似）。此时再对二阶近似后的目标函数求导，并令其导数等于 0，得到的向量表示的就是下降最快的方向。相比于梯度下降法，牛顿法的收敛速度更快。

不管是利用一阶导数的梯度下降法，还是利用二阶导数的牛顿法，其寻找最小值点的基本思想都是先确定方向，再确定步长，因而统称为“线性搜索方法”（line search）。

置信域方法

还有一类算法，其寻找最小值点的基本思路是先确定步长，以步长为参数划定一个区域，再在这个区域内寻找最快下降的方向。这类算法被称为“置信域方法”（trust region）。

具体来说，置信域算法的运行过程如下：设定一个置信域半径 s，并在以当前点为中心、以 s 为半径的封闭球形区域作为置信域，在置信域内寻找目标函数的二次近似模型的最优点，最优点和当前点之间的距离就是计算出来的备选位移。

在备选位移上，如果目标函数的二次近似产生了充分的下降，就将当前点移动到计算出的最优点，则继续按此规则迭代计算下去，并可以适当增加 s；如果目标函数的近似下降不够理想，则说明步子跨得太大，需要缩小 s 并计算出新的备选位移，直到满足终止条件。

启发式算法

除了以上算法外，还有一类被称为“启发式算法”（heuristics）的最优化方法。启发式算法的灵感来源于 20 世纪 50 年代诞生的仿生学，它将生物进化等自然现象的机理应用于现实世界复杂问题的优化之中，并取得了不俗的效果。

相对于传统的基于数学理论的最优化方法，启发式算法显得返璞归真。启发式算法的核心思想就是大自然中 " 优胜劣汰 " 的生存法则，并在算法的实现中添加了选择和突变等经验因素。

事实上，搜索越多并不意味着智能越高，智能高的表现恰恰是能够善用启发式策略，不用经过大量搜索也能解决问题。启发式算法的实例包括模拟生物进化规律的遗传算法（genetic algorithm）、模拟统计物理中固体结晶过程的模拟退火算法（simulated annealing）、模拟低等动物产生集群智能的蚁群算法（ant colony optimization）等等。

05 数学基础 | 万物皆数，信息亦然：信息论

近年来的科学研究不断证实，不确定性才是客观世界的本质属性。换句话说，上帝还真就掷骰子。不确定性的世界只能使用概率模型来描述，正是对概率的刻画促成了信息论的诞生。

1948 年，供职于美国贝尔实验室的物理学家克劳德·香农发表了著名论文《通信的数学理论》（A Mathematical Theory of Communication），给出了对信息这一定性概念的定量分析方法，标志着信息论作为一门学科的正式诞生。

信息论使用“信息熵”的概念，对单个信源的信息量和通信中传递信息的数量与效率等问题做出了解释，并在世界的不确定性和信息的可测量性之间搭建起一座桥梁。

自信息量

在信息论中，如果事件 A 发生的概率为 p(A)，则这个事件的自信息量的定义为

信源熵描述了信源每发送一个符号所提供的平均信息量，是信源总体信息测度的均值。当信源中的每个符号的取值概率相等时，信源熵取到最大值 log2n，意味着信源的随机程度最高。

条件熵

在概率论中有条件概率的概念，将条件概率扩展到信息论中，就可以得到条件熵。如果两个信源之间具有相关性，那么在已知其中一个信源 X 的条件下，另一个信源 Y 的信源熵就会减小。条件熵 H(Y∣X) 表示的是在已知随机变量 X 的条件下另一个随机变量 Y 的不确定性，也就是在给定 X 时，根据 Y 的条件概率计算出的熵再对 X 求解数学期望：

条件熵的意义在于先按照变量 X 的取值对变量 Y 进行了一次分类，对每个分出来的类别计算其单独的信息熵，再将每个类的信息熵按照 X 的分布计算其数学期望。

互信息

定义了条件信息熵后，就可以进一步得到互信息的概念

互信息等于 Y 的信源熵减去已知 X 时 Y 的条件熵，即由 X 提供的关于 Y 的不确定性的消除，也可以看成是 X 给 Y 带来的信息增益。互信息这个名称在通信领域经常使用，信息增益则在机器学习领域中经常使用，两者的本质是一样的。

在机器学习中，信息增益常常被用于分类特征的选择。对于给定的训练数据集 Y，H(Y) 表示在未给定任何特征时，对训练集进行分类的不确定性；H(Y∣X) 则表示了使用特征 X 对训练集 Y 进行分类的不确定性。信息增益表示的就是特征 X 带来的对训练集 Y 分类不确定性的减少程度，也就是特征 X 对训练集 Y 的区分度。

显然，信息增益更大的特征具有更强的分类能力。但信息增益的值很大程度上依赖于数据集的信息熵 H(Y)，因而并不具有绝对意义。为解决这一问题，研究者又提出了信息增益比的概念，并将其定义为 g(X,Y)=I(X;Y)/H(Y)。

另一个在机器学习中经常使用的信息论概念叫作“Kullback-Leibler 散度”，简称 KL 散度。KL 散度是描述两个概率分布 P 和 Q 之间的差异的一种方法，其定义为

KL 散度是对额外信息量的衡量。给定一个信源，其符号的概率分布为 P(X)，就可以设计一种针对 P(X) 的最优编码，使得表示该信源所需的平均比特数最少（等于该信源的信源熵）。

可是当信源的符号集合不变，而符合的概率分布变为 Q(X) 时，再用概率分布 P(X) 的最优编码对符合分布 Q(X) 的符号编码，此时编码结果的字符数就会比最优值多一些比特。

KL 散度就是用来衡量这种情况下平均每个字符多用的比特数，也可以表示两个分布之间的距离。

KL 散度的两个重要性质是非负性和非对称性。

非负性是指 KL 散度是大于或等于 0 的，等号只在两个分布完全相同时取到。

非对称性则是指 DKL(P∣∣Q)=DKL(Q∣∣P)，即用 P(X) 去近似 Q(X) 和用 Q(X) 去近似 P(X) 得到的偏差是不同的，因此 KL 散度并不满足数学意义上对距离的定义，这一点需要注意。

事实上，DKL(P∣∣Q) 和 DKL(Q∣∣P) 代表了两种不同的近似方式。要让 DKL(P∣∣Q) 最小，需要让 Q(X) 在 P(X) 不等于 0 的位置同样不等于 0；要让 DKL(Q∣∣P) 最小，则需要让 Q(X) 在 P(X) 等于 0 的位置同样等于 0。

最大熵原理

最大熵原理是确定随机变量统计特性时力图最符合客观情况的一种准则。对于一个未知的概率分布，最坏的情况就是它以等可能性取到每个可能的取值。

从这个角度看，最大熵原理的本质在于在推断未知分布时不引入任何多余的约束和假设，因而可以得到最不确定的结果，预测的风险也就最小。投资理财中的名言“不要把所有鸡蛋放在同一个篮子里”，就可以视为最大熵原理的一个实际应用。

将最大熵原理应用到分类问题上就可以得到最大熵模型。在分类问题中，首先要确定若干特征函数作为分类的依据。为了保证特征函数的有效性，其在模型真实分布 P(X) 上的数学期望和在由训练数据集推导出的经验分布 P~(X) 上的数学期望应该相等，即对给定特征函数数学期望的估计应该是个无偏估计量。

这样一来，每一个特征函数就对应了一个约束条件。分类的任务就是在这些约束条件下，确定一个最好的分类模型。由于除了这些约束条件之外，没有任何关于分类的先验知识，因而需要利用最大熵原理，求解出不确定性最大的条件分布，即让以下函数的取值最大化

式中的 p(y∣x) 就是分类问题要确定的目标条件分布。计算上式的最大值实质上就是一个约束优化问题，由特征函数确定的约束条件可以通过拉格朗日乘子的引入去除其影响，转化为无约束优化问题。从数学上可以证明，这个模型的解是存在且唯一的。

06 数学基础 | 明日黄花迹难寻：形式逻辑

在人工智能中，常用的知识表示方法包括数据结构和处理算法。

数据结构用于静态存储待解决的问题、问题的中间解答、问题的最终解答以及解答中涉及的知识；

处理算法则用于在已有问题和知识之间进行动态交互，两者共同构成完整的知识表示体系。

三段论

科学是不断发展的；人工智能是科学；所以，人工智能是不断发展的。

命题逻辑  和   谓词逻辑

在人工智能中应用的主要是一阶谓词逻辑。谓词逻辑是最基本的逻辑系统，也是形式逻辑的根本部分。谓词逻辑的一个特例是命题逻辑。在命题逻辑中，命题是逻辑处理的基本单位，只能对其真伪做出判断。

但命题这种表示法的局限性在于无法把其描述对象的结构及逻辑特征反映出来，也不能体现出不同事物的共同特征。假如单独给定命题“老李是小李的父亲”，在没有上下文时就无法确定老李和小李之间的关系，这个命题的真伪也就没有意义。

为了扩展形式逻辑的表示能力，在命题逻辑的基础上又诞生了谓词逻辑。谓词逻辑将命题拆分为个体词、谓词和量词，三者的意义如下：

• 个体词是可以独立存在的具体或抽象的描述对象，比如前文例子中的“老李”和“小李”；

• 谓词用于描述个体词的属性与相互关系，比如前文例子中的“是... 的父亲”；

• 量词用于描述个体词的数量关系，包括全称量词 ∀ 和存在量词 ∃。

以上三种元素可以共同构成命题。不同的命题之间则可以用逻辑联结词建立联系，由简单命题形成复合命题。按照优先级由高到低排列，逻辑联结词包括以下五种。

• 否定(¬)：复合命题 ¬P 表示否定命题 P 的真值的命题，即“非 P” 。

• 合取(∧)：复合命题 P∧Q 表示命题 P 和命题 Q 的合取，即“P 且 Q”。

• 析取(∨)：复合命题 P∨Q 表示命题 P 或命题 Q 的析取，即“P 或 Q”。

• 蕴涵(→)：复合命题 P→Q 表示命题 P 是命题 Q 的条件，即“如果 P，那么 Q”。

• 等价(↔)：复合命题 P↔Q 表示命题 P 和命题 Q 相互蕴涵，即“如果 P，那么 Q 且如果 Q，那么 P”。

谓词逻辑既可以用于表示事物的概念、状态、属性等事实性知识，也可以用于表示事物间具有确定因果关系的规则性知识。

事实性知识通常使用析取与合取符号连接起来的谓词公式表示，规则性知识则通常使用由蕴涵符号连接起来的谓词公式来表示。在一般意义上，使用谓词逻辑进行知识表示的步骤如下：

• 定义谓词及个体，确定每个谓词及每个个体的确切含义；

• 根据所要表达的事物或概念，为每个谓词中的变量赋以特定的值；

• 根据所要表达的知识的语义，用适当的逻辑联结词将各个谓词连接起来。

例如，如果要使用谓词逻辑对“所有自然数都是大于零的整数”进行知识表示，首先要将所有关系定义为相应的谓词。谓词 N(x) 表示 x 是自然数，P(x) 表示 x 大于零，I(x) 表示 x 是整数，再将这些谓词按照语义进行连接就可以得到谓词公式：

使用形式逻辑进行知识表示只是手段，其目的是让人工智能在知识的基础上实现自动化的推理、归纳与演绎，以得到新结论与新知识。就现阶段而言，人类智能与人工智能的主要区别就体现在推理能力上。

产生式系统

人工智能实现自动推理的基础是产生式系统。产生式系统以产生式的规则描述符号串来替代运算，把推理和行为的过程用产生式规则表示，其机制类似人类的认知过程，因而被早年间大多数专家系统所使用。

产生式规则通常用于表示事物之间的因果关系，其基本形式为 P→Q。它既可以用来表示在前提 P 下得到结论 Q，也可以表示在条件 P 下实施动作 Q。这里的 P 称为规则前件，它既可以是简单条件，也可以是由多个简单条件通过联结词形成的复合条件；Q 则称为规则后件。

当一组产生式规则相互配合、协同作用时，一个产生式规则生成的结论就可以为另一个产生式规则作为已知的前提或条件使用，以进一步解决更加复杂的问题，这样的系统就是产生式系统。

一般说来，产生式系统包括规则库、事实库和推理机三个基本部分。

规则库是专家系统的核心与基础，存储着以产生式形式表示的规则集合，其中规则的完整性、准确性和合理性都将对系统性能产生直接的影响。

事实库存储的是输入事实、中间结果与最终结果，当规则库中的某条产生式的前提可与事实库中的某些已知事实匹配时，该产生式就被激活，其结论也就可以作为已知事实存储在事实库中。

推理机则是用于控制和协调规则库与事实库运行的程序，包括了推理方式和控制策略。

具体而言，推理的方式可以分为三种：正向推理、反向推理和双向推理。

正向推理采用的是自底向上的方式，即从已知事实出发，通过在规则库中不断选择匹配的规则前件，得到匹配规则的后件，进而推演出目标结论。

反向推理采用的是自顶向下的方式，即从目标假设出发，通过不断用规则库中规则的后件与已知事实匹配，选择出匹配的规则前件，进而回溯已知事实。

双向推理则是综合利用正向推理和反向推理，使推理从自顶向下和自底向上两个方向进行，直到在某个中间点汇合，这种方式具有更高的效率。

自动推理虽然在数学定理的证明上显示出强大的能力，可解决日常生活中的问题时却远远谈不上智能，其原因在于常识的缺失。对于人类而言，常识的建立是通过社会化的成长过程实现的。

可计算机没办法像人类一样在成长中达成理解，因而常识这一智能的先决条件只能以形式化的方式被灌输到硬盘与内存之中。这要求将一般成年人的知识和信念进行显式的表达，并加以灵活的组织和运用。

哥德尔不完备性定理

谈论人工智能中的形式逻辑，最终的不可回避的本质问题在于哥德尔不完备性定理。

1900 年，德国数学家大卫·希尔伯特在巴黎国际数学家代表大会上提出了 20 世纪 23 个最重要的数学问题，其中的第二问题便是算术公理系统的无矛盾性。

1931 年，奥地利数学家库尔特·哥德尔对这个问题给出了否定的答案，即第一不完备性定理：

在任何包含初等数论的形式系统中，都必定存在一个不可判定命题。

通过这个定理，哥德尔证明了公理化系统的阿喀琉斯之踵在于对自指的无能为力，下面的语句就是个典型的自指语句：

本数学命题不可以被证明。

首先，这个数学命题所讨论的对象不是别的，恰恰是它自己。“本数学命题”就是对整个命题的指代。其次，该命题给出了一个逻辑判断，即这条命题是不可以被证明的。哥德尔证明了这个命题既不能被证实也不能被证伪，无情戳破了数学公理化系统同时具备一致性和完备性的黄粱一梦。

不完备性定理对人工智能的影响在于对“认知的本质是计算”这一理论基础的理解。从“认知即计算”的角度出发，基于计算机的人工智能如果想要达到近似人类的思维能力，也必须建立起“自我”的概念，这就无疑会导致自指的出现，也将成为不完备性定理的活靶子。

在哥德尔不完备性定理的阴影下，基于图灵可计算概念的“认知可计算主义”研究纲领已经显示出其极大的局限。今天，依靠人工神经网络逐渐崛起的连接主义学派大放异彩，与此同时，以形式逻辑为依据的符号主义学派则已经走向没落。

但抛开学术路径的不同，人类智能与人工智能的本质区别到底在哪里，也许这才是不完备性定理留给我们的最大谜团。

（课外辅导）数学基础 | 拓展阅读参考书