实现二叉树的基本操作与OJ练习

目录

1.二叉树的基本操作

1.1二叉树基本操作完整代码 

 1.2检测value值是否存在

1.3层序遍历

1.4判断一棵树是不是完全二叉树 

 2.OJ练习

2.1平衡二叉树

2.2对称二叉树 

2.3二叉树遍历 

---

1.二叉树的基本操作

1.1二叉树基本操作完整代码 

public class BinaryTree {
    static class TreeNode{
        public char val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(char val) {
            this.val = val;
        }
    }
    //使用穷举，实现一棵树
    public TreeNode creatTree() {
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');
        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left = F;
        C.right = G;
        E.right = H;
        return A;
    }
    // 前序遍历  根 左子树 右子树
     public void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.print(root.val + " ");
        preOrder(root.left);
        preOrder(root.right);
    }
    // 中序遍历 左 根 右
    public void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }
    // 后序遍历 左 右 根
    public void postOrder(TreeNode root){
        if (root == null) {
            return;
        }
        inOrder(root.left);
        inOrder(root.right);
        System.out.print(root.val + " ");
    }
    // 获取树中节点的个数
    public int sizeCount;
    public void size(TreeNode root){
        if(root == null) {
            return;
        }
        sizeCount++;
        size(root.left);
        size((root.right));
    }
    //子问题
    public int  size2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return size2(root.left) + size2(root.right) + 1;
    }
    // 获取叶子节点的个数
    public int leafCount;
    //遍历求解
    public void getLeafNodeCount(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left == null && root.right == null){
            leafCount++;
        }
        getLeafNodeCount(root.left);
        getLeafNodeCount(root.right);
    }
    // 子问题思路-求叶子结点个数
    public int getLeafNodeCount2(TreeNode root){
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1;
        }
        //左子树的叶子节点+右子树的叶子节点
        return getLeafNodeCount2(root.left) +
                getLeafNodeCount2(root.right);
    }
    // 获取第K层节点的个数
    public int getKLevelNodeCount(TreeNode root,int k) {
        if (root == null) {
            return 0;
        }
        if (k == 1) {
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1) +
                getKLevelNodeCount(root.right,k-1);
    }
    // 获取二叉树的高度
    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return Math.max(leftHeight,rightHeight) + 1;
    }
    // 检测值为value的元素是否存在
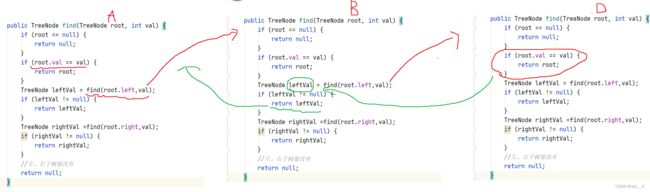
    public TreeNode find(TreeNode root, int val) {
        if (root == null) {
            return null;
        }
        if (root.val == val) {
            return root;
        }
        TreeNode leftVal = find(root.left,val);
        if (leftVal != null) {
            return leftVal;
        }
        TreeNode rightVal =find(root.right,val);
        if (rightVal != null) {
            return rightVal;
        }
        //左、右子树都没有
        return null;
    }
    //层序遍历
    public void levelOrder(TreeNode root){
        if (root == null) {
            return;
        }
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val+" ");
            if(cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }
    //判断一棵树是不是完全二叉树
   public boolean isCompleteTree(TreeNode root){
        if(root == null) {
            return true;
        }
       Queue queue = new LinkedList<>();
       queue.offer(root);
       while (!queue.isEmpty()) {
           TreeNode cur = queue.poll();
           if (cur != null) {
               queue.offer(cur.left);
               queue.offer(cur.right);
           } else {
               break;
           }
       }
       //走到这里两种情况 1.队列为空 2.遇到break
       while (!queue.isEmpty()) {
           TreeNode cur = queue.peek();
           if (cur != null) {
               queue.poll();
           } else {
               return false;
           }
       }
        return true;
   }
}

 1.2检测value值是否存在

题解：

1.3层序遍历

题解：

层序遍历：就是从上到下，从左到右，依次遍历。前序、中序、后序本质上都是从上到下。

所以，就是要解决从左到右。

可以引入队列解决(先进先出)，如果不是空树，先把根节点放到队列里，此时队列不为空，当该节点出队是，用cur记录，不为空并把该节点的左、右节点放进队列。

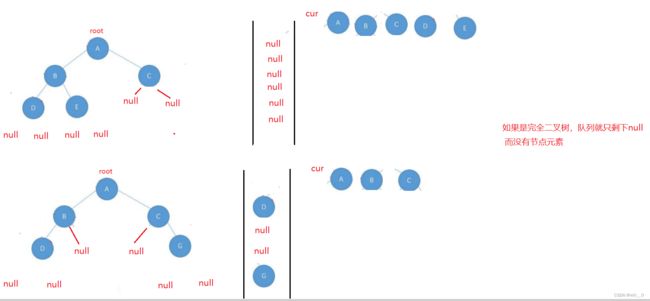
1.4判断一棵树是不是完全二叉树 

题解：

也是引入队列解决，当cur不为空把该节点的左、右节点放进队列；否则跳出循环。

在遍历队列，是否都为null.

 2.OJ练习

2.1平衡二叉树

题解：

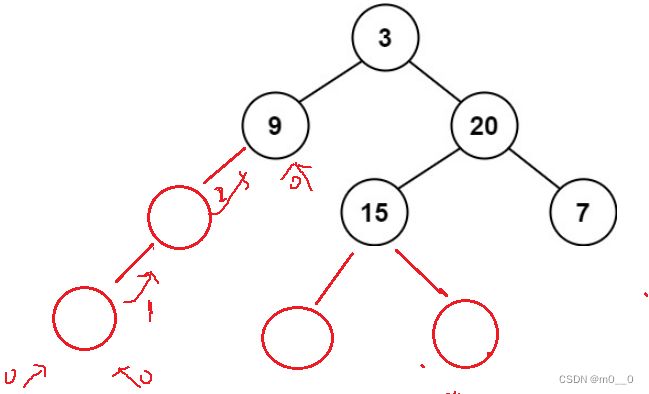
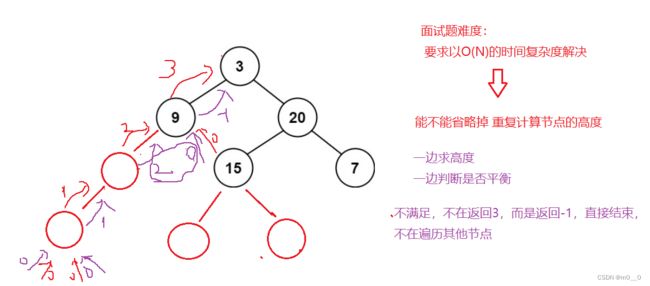
是不是一颗平衡二叉树，当前根节点的左右子树的高度差的绝对值<=1&&根左子树平衡&&根右子树平衡。

如下代码：就会发现求节点3的高度，把每个节点都求了一遍。 求节点9的高度时，也把每个节点都求了一遍。就会有很高度重复求，maxDepth有N个节点，最坏时间复杂度:N*N=N^2.

    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return Math.abs(leftHeight - rightHeight) <= 1 &&
                isBalanced(root.left)&&isBalanced(root.right);

    }
   public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return Math.max(leftHeight, rightHeight) + 1;
    }

 省略掉重复计算的高度！

    public boolean isBalanced2(TreeNode root) {
        if(root == null) {
            return true;
        }

        return maxDepth(root) >= 0;

    }
    public int maxDepth2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = maxDepth2(root.left);
        if(leftHeight < 0) {
            return -1;
        }
        int rightHeight = maxDepth2(root.right);
        if(leftHeight >= 0 && rightHeight >= 0
                && Math.abs(leftHeight - rightHeight) <= 1){
            return Math.max(leftHeight,rightHeight) + 1;
        } else {
            return -1;
        }
    }

2.2对称二叉树 

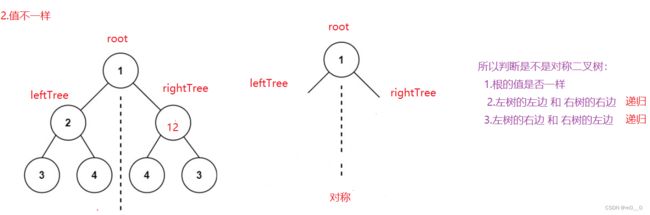
     题目描述：给你一个二叉树的根节点 root ， 检查它是否轴对称。 

题解：

    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }
        return isSameTree2(root.left,root.right);

    }
    public boolean isSameTree2(TreeNode lefTree,TreeNode rightTree){
        if(lefTree == null && rightTree != null || lefTree != null && rightTree == null) {
            return false;
        }
        if(lefTree == null && rightTree == null) {
            return true;
        }
        if(lefTree.val != rightTree.val) {
            return false;
        }
        return isSameTree2(lefTree.left,rightTree.right)
                &&isSameTree2(lefTree.right,rightTree.left);
    }

2.3二叉树遍历 

题目描述：编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

题解： 

  遍历这个字符串，根据前序遍历的方式，创建二叉树

   class TreeNode {
        char val;
        TreeNode left;
        TreeNode right;

        public TreeNode(char val) {
            this.val = val;
        }
    }

    // 注意类名必须为 Main, 不要有任何 package xxx 信息
    public class Main {
        public static int i = 0;
        public static void main(String[] args) {
            Scanner in = new Scanner(System.in);
            // 注意 hasNext 和 hasNextLine 的区别
            while (in.hasNextLine()) { // 注意 while 处理多个 case
                String str = in.nextLine();

                TreeNode root = creatTree(str);

                inOrder(root);
            }
        }
        public static TreeNode creatTree(String str) {
            //1.遍历字符串
            //2.创建二叉树
            TreeNode root = null;
            if(str.charAt(i)!= '#') {
                root = new TreeNode(str.charAt(i));
                i++;
                root.left = creatTree(str);
                root.right = creatTree(str);

            } else{
                i++;
            }
            //返回根节点
            return root;
        }
        public static void inOrder(TreeNode root) {
            if(root == null) {
                return;
            }
            inOrder(root.left);
            System.out.print(root.val+" ");
            inOrder(root.right);
        }
    }