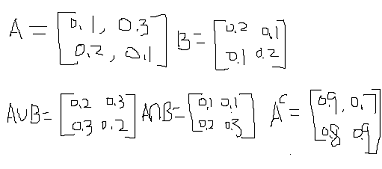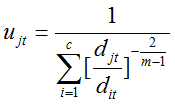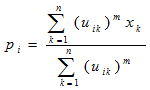文本聚类python fcm_机器学习笔记----Fuzzy c-means(FCM)模糊聚类详解及matlab实现

前言：这几天一直都在研究模糊聚类。感觉网上的文档都没有一个详细而具体的讲解，正好今天有时间，就来聊一聊模糊聚类。

一：模糊数学

我们大家都知道计算机其实只认识两个数字0,1。我们平时写程序其实也是这样if 1 then do.永远这种模式，在这种模式中，一个元素要么属于这个集合，要么不属于这个集合，但是对我们现在介绍的模糊集来说，某个元素可能部分属于这个集合，又可能部分属于另外的集合，显然，例如，一个男人(1表示)，一个女人(0表示)，但是随着科学技术的发展，出现了人妖这个生物(可能0.3属于男人，0.7属于女人).这样如果用0,1就显得不太恰当了，那我们该如何表示呢，且听我慢慢道来。

开始之前先介绍模糊数学几种不同的名称：

模糊集：给定一个论域 U ，那么从 U 到单位区间 [0,1] 的一个映射

称为 U 上的一个模糊集，或 U 的一个模糊子集. 模糊集可以记为 A 。 映射(函数) μA(·) 或简记为 A(·) 叫做模糊集 A 的隶属函数。 对于每个 x ∈ U ， μA(x) 叫做元素 x 对模糊集 A 的隶属度。

模糊逻辑：它是一种相对于传统是或者不是的二值逻辑而言的。例如下图：

，如果这个人在B里面，那么很好理解，人在B里面为1，但是如果出现下列这种情况呢：

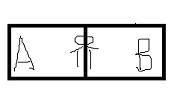，显然用上述的逻辑就行不通了，但是可以这样表示在(A,B)=(0，6，0.4),o,6在A, 0,4在B，这样完美解决。其实拓展成3，4,5也都一样。类似于，我们看周星驰的赌侠，反派用电脑分析，牌的可能性。其实跟这个道理差不多

模糊矩阵：设R=(rij)mxn,若0<=rij<=1,那么称该矩阵为模糊矩阵。若矩阵元素只有0,1的时候成为布尔矩阵。如果对角线上都是一，则这个矩阵称为自反矩阵、

模糊矩阵的关系以及并交与计算：

假设

，

都是模糊矩阵。

交运算：

并运算：

余运算：

例子如下(画的比较丑，请见谅)：

模糊矩阵的合成：

设

为模糊矩阵，

，为A与B的合成，其中

为模糊矩阵的幂。

定义：若A为n阶方阵，定义:

首先模糊数学的基础就补充到这里了。下面来看看。FCM算法。

二 FCM算法

2.1 FCM算法简介

FCM算法首先是由E. Ruspini提出来的，后来J. C. Dunn与J. C. Bezdek将E. Ruspini算法从硬聚类算法推广成模糊聚类算法。FCM算法是基于对目标函数的优化基础上的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度，该隶属程度用一个数值来表示。FCM算法是一种无监督的模糊聚类方法，在算法实现过程中不需要人为的干预。这种算法的不足之处:首先，算法中需要设定一些参数，若参数的初始化选取的不合适，可能影响聚类结果的正确性;其次，当数据样本集合较大并且特征数目较多时，算法的实时性不太好。

2.2 FCM算法的实现原理

我们的FCM算法是从硬划分而来的。

硬划分FCM算法的目标函数：

。U表示原矩阵，p表示聚类中心，dik表示样本点xk与第i个类的样本原型pi之间的失真度，一般是用两个向量之间的距离表示。

软划分FCM的目标函数：

。Uik表示xk与第i类样本的隶属度。

一般性模糊聚类分析的目标函数：

，其中m>1.dik是一种距离范数，可以表示为

，A表示权重。

求解过程如下(把我以前写的截图发来)：

得到：

求解聚类中心：

得到聚类中心：

FCM算法执行流程：

安利一波(百度脑图，这是我认为百度做的比较有良心的东西了。我这个就是用百度脑图画的)

三 FCM的Matlab实现

function [U,P,Dist,Cluster_Res,Obj_Fcn,iter]=fuzzycm(Data,C,plotflag,M,epsm)

% 模糊 C 均值聚类 FCM: 从随机初始化划分矩阵开始迭代

% [U,P,Dist,Cluster_Res,Obj_Fcn,iter] = fuzzycm(Data,C,plotflag,M,epsm)

% 输入:

% Data: N×S 型矩阵,聚类的原始数据,即一组有限的观测样本集,

% Data 的每一行为一个观测样本的特征矢量,S 为特征矢量

% 的维数,N 为样本点的个数

% C: 聚类数,1

% plotflag: 聚类结果 2D/3D 绘图标记,0 表示不绘图,为缺省值

% M: 加权指数,缺省值为 2

% epsm: FCM 算法的迭代停止阈值,缺省值为 1.0e-6

% 输出:

% U: C×N 型矩阵,FCM 的划分矩阵

% P: C×S 型矩阵,FCM 的聚类中心,每一行对应一个聚类原型

% Dist: C×N 型矩阵,FCM 各聚类中心到各样本点的距离,聚类中

% 心 i 到样本点 j 的距离为 Dist(i,j)

% Cluster_Res: 聚类结果,共 C 行,每一行对应一类

% Obj_Fcn: 目标函数值

% iter: FCM 算法迭代次数

% See also: fuzzydist maxrowf fcmplot

if nargin<5

epsm=1.0e-6;

end

if nargin<4

M=2;

end

if nargin<3

plotflag=0;

end

[N,S]=size(Data);m=2/(M-1);iter=10000;

Dist(C,N)=0; U(C,N)=0; P(C,S)=0;

% 随机初始化划分矩阵

U0 = rand(C,N);

U0=U0./(ones(C,1)*sum(U0));

% FCM 的迭代算法

while true

% 迭代计数器

iter=iter+1;

% 计算或更新聚类中心 P

Um=U0.^M;

P=Um*Data./(ones(S,1)*sum(Um'))';

% 更新划分矩阵 U

for i=1:C

for j=1:N

Dist(i,j)=fuzzydist(P(i,:),Data(j,:));

end

end

U=1./(Dist.^m.*(ones(C,1)*sum(Dist.^(-m))));

% 目标函数值: 类内加权平方误差和

if nargout>4 | plotflag

Obj_Fcn(iter)=sum(sum(Um.*Dist.^2));

end

% FCM 算法迭代停止条件

if norm(U-U0,Inf) break

end

U0=U;

end

% 聚类结果

if nargout > 3

res = maxrowf(U);

for c = 1:

v = find(res==c);

Cluster_Res(c,1:length(v))=v;

end

end

% 绘图

if plotflag

fcmplot(Data,U,P,Obj_Fcn);

end

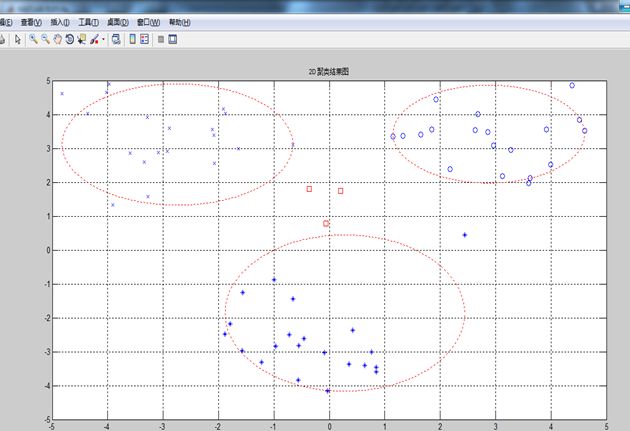
我用的数据集聚类结果：

感觉效果好挺好的。

今天的模糊聚类就讲到这里了希望大家点个关注，以及批评指正。