【nature论文精读】Impedance-based forecasting of lithium-ion battery performance amid uneven usage

【nature论文精读】 Impedance-based forecasting of lithium-ion battery performance amid uneven usage

论文链接：https://www.nature.com/articles/s41467-022-32422-w.pdf

Accurate forecasting of lithium-ion battery performance is essential for easing consumer concerns about the safety and reliability of electric vehicles. Most research on battery health prognostics focuses on the research and development setting where cells are subjected to the same usage patterns. However, in practical operation, there is great variability in use across cells and cycles, thus making forecasting challenging. To address this challenge, here we propose a combination of electrochemical impedance spectroscopy measurements with probabilistic machine learning methods. Making use of a dataset of 88 commercial lithium-ion coin cells generated via multistage charging and discharging (with currents randomly changed between cycles), we show that future discharge capacities can be predicted with calibrated uncertainties, given the future cycling protocol and a single electrochemical impedance spectroscopy measurement made immediately before charging, and without any knowledge of usage history. The results are robust to cell manufacturer, the distribution of cycling protocols, and temperature. The research outcome also suggests that battery health is better quantified by a multidimensional vector rather than a scalar state of health.

锂离子电池性能的准确预测对于缓解消费者对电动汽车安全性和可靠性的担忧至关重要。大多数关于电池健康预测的研究都集中在电池处于相同使用模式的研发环境中。然而，在实际操作中，跨细胞和周期的使用存在很大的可变性，因此预测具有挑战性。为了解决这一挑战，我们在这里提出了电化学阻抗谱测量与概率机器学习方法的结合。利用88个通过多级充放电产生的商业锂离子硬币电池的数据集(在周期之间电流随机变化)，我们表明，考虑到未来的循环协议和充电前立即进行的单一电化学阻抗谱测量，并且不需要任何使用历史知识，可以用校准的不确定性预测未来的放电容量。结果对电池制造商、循环协议的分布和温度具有鲁棒性。研究结果还表明，电池健康状况可以通过多维向量而不是标量状态来更好地量化。

Electrification of the transportation industry is now taking place at an increasingly rapid pace, enabling significant strides towards a carbon neutral future. Fundamental to this transition has been the development of the lithium-ion battery, which powers the majority of electric vehicles (EVs) on the road today. Notwithstanding the environmental benefits of this transition, reliance on the lithium-ion battery poses significant challenges, with consumer concerns including range anxiety, fear of battery failure and charging time. Easing these concerns demands the ability to accurately forecast battery performance, and specifically when usage conditions are variable.

交通运输业的电气化正在以越来越快的速度进行，使我们能够在实现碳中和的未来方面取得重大进展。这一转变的基础是锂离子电池的发展，目前在路上行驶的大多数电动汽车都是由锂离子电池驱动的。尽管这种转变对环境有利，但对锂离子电池的依赖带来了重大挑战，消费者担心的问题包括里程焦虑、电池故障和充电时间。缓解这些担忧需要准确预测电池性能的能力，特别是当使用条件变化时。

The key challenge is the heterogeneity of the battery. Each user uses their car differently, and even across a single battery pack not all cells are necessarily charged or discharged with identical current.

关键的挑战是电池的异质性heterogeneity。每个用户使用汽车的方式都不同，即使是在一个电池组中，也不是所有的电池都必须以相同的电流充电或放电。

These differences mean that each cell’s internal state, including the extent of lithium plating or electrode cracking, can vary significantly both at an intra-pack and inter-pack level.

这些差异意味着每个电池的内部状态，包括锂电镀或电极开裂的程度，在电池组内和电池组间的水平上都可能存在显著差异。

To quantify the extent of degradation within cells, and to identify cells that have reached their End of Life (in EVs, this is typically defined as the point at which the discharge capacity has reduced to 80% of the nominal capacity), the scalar State of Health (SOH) metric is typically adopted, measured using previous cycle discharge capacity or internal resistance8–13. The problem with this approach is that batteries with the same numerical SOH do not necessarily exhibit identical levels of each degradation process (for example, lithium plating or electrode cracking), yet the impact of future cell usage on the cell’s future performance and degradation pathway depends significantly on the type of degradation that has already occurred14–16. Accurate forecasting of battery performance demands a non-invasive approach to acquire information about the cell state at a microscopic level.

为了量化锂电池单体内的退化程度，并识别已达到生命终点的锂电池单体(在电动汽车中，这通常定义为放电容量降低到标称容量的80%的点)，通常采用标量健康状态(SOH)度量，使用以前的循环放电容量或内阻测量。这种方法的问题是，具有相同数值SOH的电池在每个降解过程中不一定表现出相同的水平(例如，锂电镀或电极开裂)，但未来电池使用对电池的性能和降解途径的影响取决于已经发生的降解。电池性能的准确预测需要一种非侵入性的方法来获取微观水平上电池状态的信息。

Both short and long timescale forecasting of battery performance are of interest in battery prognostics. Over a short timescale, predicting how the battery would respond to a particular charging and discharging protocol can be used to develop optimal charging protocols. Short-term forecasting also encompasses SOH estimation: here, the aim is to predict the battery’s discharge capacity or internal resistance under a specific, standardised cycling protocol. Over a long timescale, the focus is on predicting the remaining useful life, end of life, or the ‘knee-point’ in the battery’s life trajectory at which degradation accelerates.

电池性能的短和长时间尺度预测在电池预测中都是感兴趣的。在短时间内，预测电池将如何响应特定的充放电协议，可用于开发最佳充电协议。短期预测还包括SOH估计:在这里，目标是在特定的标准化循环协议下预测电池的直流电阻容量或内阻。在很长一段时间内，研究的重点是预测剩余的使用寿命，即寿命的结束，或者电池寿命轨迹中加速退化的“膝点”。

Approaches to both types of forecasting can be subdivided into empirical, physics-based, and data-driven models, with some models being a hybrid of these.
Empirical approaches have been used to model long-term capacity fade with power laws but assume fixed operation over battery life and do not account for intrinsic differences in cell state at start of life. These approaches assume that all cells of the same chemistry will fade in the same way if operated in the same way, which is not observed in practice.
In physics-based approaches, the battery is either modelled mechanistically using first principles analysis of internal physical and electrochemical processes, or using equivalent circuit modelling, which models the cell as a circuit comprising resistors and capacitors that are representative of the underlying electrochemical processes. Mechanistic models aim to capture how the battery voltage responds to an externally applied current (or vice versa), which can be used to predict optimal charging protocols.However, the parameters of such models need to be updated for each individual cell and typically suffer from non-identifiability – several sets of model parameters could explain the observed data equally well, but would make drastically different predictions on test cells or on the same cell later in its life.

这两种类型的预测方法可以细分为经验模型、基于物理的模型和数据驱动模型，有些模型是这些模型的混合。
经验方法Empirical approaches已被用于模拟长期容量随功率定律衰减，但假设在电池寿命期间固定运行，不考虑电池寿命开始时状态的内在差异。这些方法假设所有具有相同化学性质的锂电池单体如果以相同的方式操作，将以相同的方式褪色，这在实践中没有观察到。
在基于物理的方法physics-based approaches中，电池要么使用内部物理和电化学过程的第一性原理分析进行机械建模，要么使用等效电路建模，将电池建模为包含代表底层电化学过程的电阻和电容的电路。 机械模型旨在捕捉电池电压如何响应外部施加的电流(反之亦然)，可用于预测最佳充电协议。然而，这种模型的参数需要为每个单独的锂电池单体更新，并且通常存在不可识别性——几组模型参数可以同样很好地解释观察到的数据，但会对测试锂电池单体或同一锂电池单体后期的生命周期做出截然不同的预测。

For circuit-based models, the parameters of the circuit can be fitted to either current-voltage data, or to electrochemical impedance spectra. The circuit parameters can then be used to forecast capacity degradation under standardised use conditions or to simulate the effect of different usage conditions on battery pack performance30. However, it is challenging to capture every degradation mode in an analytical model. Further, a new set of model parameters must be learnt for each cell from cycle to cycle, making it challenging to infer a general cell-to-cell model.

对于基于电路的模型，电路的参数可以拟合到电流-电压数据，或电化学阻抗谱。然后，电路参数可用于预测标准化使用条件下的容量退化或模拟不同使用条件对电池组性能的影响。然而，在分析模型中捕获每种退化模式.是具有挑战性的。此外，从一个周期到另一个周期，每个细胞都必须学习一组新的模型参数，这使得推断一个一般的细胞到细胞模型具有挑战性。

Purely data-driven approaches to forecasting use raw data as input to a machine learning algorithm to forecast long term capacity fade, resistance increase and remaining useful life. Feature - based data-driven approaches applied machine learning on features extracted from the charging or discharging curve to predict discharge capacity, remaining useful life, and abrupt capacity decays.
Innovations in extracting features from charge/discharge curves and machine learning approaches for modelling time-series data have enabled significant improvements in the accuracy of predictions.
Further studies showed that using features of the discharge curve across a small number of initial cycles, it is possible to train machine learning models that can generalise to different cell chemistries.
Going beyond charging and discharging curves, approaches such as electrochemical impedance spectroscopy (EIS), early cycle Coulombic efficiency, current interruption and acoustic time-of-flight analysis have been used for degradation forecasting. These approaches provide a fuller description of battery state – for example, EIS captures the response of the cell over a broad frequency range, with different frequencies correlating to distinct physical, chemical and mechanical changes in the active material. Data - driven methods typically utilise data generated in the laboratory setting, where cells are charged and discharged in the same way over the entirety of their lifetimes, thus the impact of variable cell usage on future performance can be ignored (see Fig. 1). However, extrapolating the models developed for laboratory setting to field data or other realistic usage profiles such as the Worldwide Harmonized Light Vehicles Test Cycles (WLTC), where cells are cycled in vastly different ways over their lifetimes, has proved a major challenge.

纯数据驱动的预测方法使用原始数据作为机器学习算法的输入，来预测长期容量衰退、阻力增加和剩余使用寿命。数据驱动方法将机器学习应用于从充电或放电曲线中提取的特征，以预测放电容量、剩余使用寿命和容量突然衰减。

从充放电曲线中提取特征和时间序列数据建模的机器学习方法的创新，使得预测的准确性有了显著提高。
进一步的研究表明，利用少量初始周期的放电曲线特征，可以训练出可以推广到不同细胞化学性质的机器学习模型。

除了充电和放电曲线之外，电化学阻抗谱(EIS)、早周期库仑效率、电流中断和声学飞行时间分析等方法已用于降解预测。
这些方法提供了对电池状态更全面的描述——例如，EIS捕获了电池在宽频率范围内的响应，不同的频率与活性材料中不同的物理、化学和机械变化相关。
数据驱动方法方法通常利用在实验室环境中产生的数据，其中电池在其整个生命周期内以相同的方式充电和放电，因此可以忽略可变电池使用对未来性能的影响(见图1)。然而，将为实验室环境开发的模型外推算到现场数据或其他实际使用概况，如全球协调轻型车辆测试周期(WLTC)，锂电池单体在其一生中以截然不同的方式循环，这已被证明是一个重大挑战。

Fig. 1 | Schematic comparison of the proposed approach to previous research works. Feature-based methodologies for degradation prediction have focused on constant charging protocols (the blue/red curve denotes the charge/discharge phase), using features from capacity–voltage curves as input. This necessitates knowledge of historic charging data. Our approach considers variable charging protocols (the shaded blue/red region denotes the range of currents that the charge/discharge protocols are drawn from), which is more comparable to the EV setting. Further, we employ the electrochemical impedance spectrum measured just before charging as input, without any knowledge of historic data, and predict the impact of different future usage protocols on the discharge capacity.

图1 |所提方法与以往研究工作的对比示意图。
基于特征的退化预测方法专注于恒定充电协议(蓝色/红色曲线表示充电/放电阶段)，使用容量-电压曲线的特征作为输入。这强调了历史收费数据的知识的重要性。
我们的方法考虑了可变充电协议(蓝色/红色阴影区域表示充电/放电协议的电流范围)，这更类似于电动汽车设置。此外，我们使用充电前测量的电化学阻抗谱作为输入，不了解任何历史数据，并预测未来不同使用协议对放电容量的影响。

In this work, we seek to identify whether there exists a sufficiently informative marker of cell health that can be used to forecast shortterm and longer term future performance, amid uneven historical and future cell usage. Figure 1 provides an illustration of our approach, and how it differs from previous approaches. We find that upon acquisition of an EIS spectrum just before charging, both next cycle and longer term cell capacity can be predicted with a test error of less than 10%.

When testing on cells subjected to similar cycling conditions to those used to train the model, our model achieves comparable accuracy to state-of-the-art forecasting models (8.2% test error versus 8.8% test error), except that our model enables forecasting with no access to any historical data, whereas previous state-of-the-art models require historical data from the cell’s cycling trajectory. In addition, when extrapolating to different operating temperatures, our model significantly outperforms the state-of-the-art model, achieving a 57% reduction in test error (from 34.2% to 14.6%).

在这项工作中，我们试图确定是否存在一个足够信息的锂电池单体健康标记，可以用来预测短期和长期的未来性能，在不平衡的历史和未来锂电池单体使用。图1展示了我们的方法，以及它与以前的方法的不同之处。我们发现，在充电前获取EIS频谱，可以预测下一个周期和更长期的电池容量，测试误差小于10%。

当在与用于训练模型的周期条件相似的锂电池单体上进行测试时，我们的模型达到了与最先进的预测模型相当的精度(8.2%的测试误差对8.8%的测试误差)，除了我们的模型可以在不访问任何历史数据的情况下进行预测，而以前的最先进的模型需要来自细胞周期轨迹的历史数据。此外，当外推到不同的工作温度时，我们的模型显著优于最先进的模型，测试误差降低了57%(从34.2%降至14.6%)。

We observe that our model is data-efficient, requiring just eight cells to attain a test error of less than 10%. Crucially, our approach is robust to dataset shift, attaining a test error of less than 7% on a dataset with a different distribution of cycling patterns to the training set. This is important for deployment in the field where driving patterns may be different from those used to train the model. We additionally demonstrate that, if available, using additional features based on historical capacity–voltage data can serve to augment the state representation and reduce average test error by up to 25%. Our approach is robust with respect to cell manufacturer, average usage pattern and operating temperature.

我们观察到，我们的模型是数据高效 data-efficient的，只需要8个单元就可以获得小于10%的测试误差。
至关重要的是，我们的方法对数据集偏移dataset shift具有鲁棒性，在具有不同循环模式分布的数据集上获得小于7%的测试误差。这对于在驾驶模式可能不同于用于训练模型的驾驶模式的现场部署非常重要。
我们还证明，如果可用，使用基于历史容量-电压数据的附加特征可以增强状态表示，并将平均测试误差降低高达25%。我们的方法在电池制造商、平均使用模式和操作温度方面是稳健的。

Further, our work fills a gap in publicly available data by contributing a large corpus of cycling data on cells under dynamic working conditions. Our work focuses on a set of idealised usage distributions rather than realistic driving profile in order to demonstrate the extent of generalisability of the model. Our work departs from the NASA randomised usage dataset, which randomly cycles cells for 50 cycles before measuring the next cycle discharge capacity after charging via a ‘reference’ protocol. Although several models for forecasting degradation under randomised conditions have been built based on this data, the effect of a single protocol on next cycle discharge capacity cannot be disentangled, and there is a need for a reference charge/discharge protocol every few cycles which does not concord with typical field usage.

此外，我们的工作通过提供动态工作条件下锂电池单体循环数据的大型语料库，填补了公开数据的空白。我们的工作侧重于一组理想化的使用分布，而不是现实的驾驶剖面，以证明模型的泛化程度。我们的工作脱离了NASA的随机使用数据，该数据随机循环电池50个周期，然后通过“参考”协议充电后测量下一个周期的放电容量。尽管基于这些数据已经建立了在随机条件下预测退化的几个模型，但单个协议对下一个周期放电容量的影响无法解耦，并且需要每隔几个周期就有一个参考充电/放电协议，这与典型的现场使用情况不一致。

Result

Data generation

For this study, we generate two separate datasets corresponding to commercial LiR coin cells 锂离子可充电钮扣电池 purchased from two different manufacturers, which allows us to test whether our approach is robust with respect to cell manufacturer.

在这项研究中，我们生成了两个独立的数据集，对应于从两个不同的制造商购买的商业锂离子可充电钮扣电池，这使我们能够测试我们的方法对于电池制造商是否稳健。

The first dataset corresponds to 40 Powerstream LiR 2032 coin cells (nominal capacity 1C = 35 mAh). We subject 24 cells to a sequence of randomly selected charge and discharge currents at 23 ± 2 °C for 110–120 full charge/discharge cycles. Each cycle consists of an initial diagnosis of battery state, involving acquisition of the galvanostatic EIS spectrum, followed by usage, involving a charging and discharging stage. Charging and discharging consist of a two stage and one stage Constant Current (CC) protocol, respectively; the currents are randomly selected at each cycle in the ranges 70–140 mA (2–4 C ) , 35–105 mA (1–3 C), and 35–140 mA (1–4 C) respectively. To test the model’s robustness to domain shift, we additionally cycle the remaining 16 cells under the same conditions as above, except now fixing the discharge current for all cells and cycles at 52.5mA (1.5 C) instead of randomly changing the discharge current at each cycle. The space of protocols considered is illustrated in Fig. 2 and an example of the capacity trajectories of three cells is provided in Supplementary Fig. 1 for illustration of the difference from typical monotonic capacity fade experiments. A complete description of cycling protocols is provided in the Methods and the full set of operating conditions that each cell is subjected to is detailed in Supplementary Table 1.Having used the first dataset to confirm the approach can successfully forecast discharge capacity several cycles ahead, we later significantly expand our analysis to explore the model’s robustness to cell manufacturer, changes to usage pattern and operating temperature. To achieve this, we cycle an additional 48 cells from a second manufacturer, RS Pro (nominal capacity 40 mAh), under a much wider range of usage patterns. In this case, each cell is again subjected to 100 cycles of two-stage CC charging, and one-stage CC discharging, with the three rates randomly selected at the start of each cycle. However, we now make the problem more challenging by having a different distribution of currents for each cell, to replicate the scenario in which different battery users have different average usage patterns to each other, but still exhibit random cycle-to-cycle behaviour. Of these cells, sixteen are also cycled at a higher operating temperature of 35 °C.

第一个数据集对应于40个Powerstream LiR 2032锂离子可充电钮扣电池(标称容量1C = 35 mAh)。我们将24个电池置于随机选择的23±2°C充放电电流序列中，进行110-120个完整的充放电循环。每个周期包括电池状态的初始诊断，包括恒流EIS谱的获取，然后是使用，包括充电和放电阶段。充电和放电分别由两级和一级恒流(CC)协议组成;电流分别在70-140 mA (2-4 C)、35-105 mA (1-3 C)和35-140 mA (1-4 C)的范围内随机选择。

为了测试模型对域移位的鲁棒性，我们在上述相同的条件下对其余16个单元进行循环，除了现在将所有单元的放电电流固定在52.5mA (1.5 C)，而不是在每个周期随机改变放电电流。

所考虑的协议空间如图2所示，补充图1中提供了三个单元的容量轨迹示例，以说明与典型单调容量衰减实验的差异。方法中提供了对循环方案的完整描述，补充表1详细描述了每个单元所承受的全套操作条件。在使用第一个数据集确认该方法可以成功预测几个周期前的放电容量后，我们随后显著扩展了我们的分析，以探索模型对电池制造商、使用模式变化和工作温度的相关性。

为了实现这一目标，我们在更广泛的使用模式下，从另一家制造商RS Pro(标称容量40毫安时)额外循环48个电池。在这种情况下，每个电池再次受到100个两级CC充电和一级CC放电的循环，在每个循环开始时随机选择三个速率。然而，我们现在通过为每个电池提供不同的电流分布使问题更具挑战性，以复制不同的电池用户彼此具有不同的平均使用模式，但仍然表现出随机的周期到周期行为的场景。在这些电池中，有16个也在35°C的较高工作温度下循环。

Fig. 2 | Proposed charge-discharge protocol. We generate battery cycling data by subjecting cells to a sequence of random charge and discharge currents. We apply two stages of constant current (CC) charging for up to 15 min each, with currents drawn from the ranges 70–140 mA (2–4 C ) a n d 3 5–105 mA (1–3 C), respectively (the blue shaded region). If the safety threshold voltage of 4.3 V is reached before the time limit, then charging is stopped. During discharging, a single constant discharge current, randomly selected in the range 35–140 mA (1–4 C), is applied (the red shaded region), until the voltage drops to 3.0 V.

图2 |提出的充放电协议。我们通过将电池置于一系列随机充放电电流中来生成电池循环数据。我们采用两级恒流(CC)充电，每级充电长达15分钟，电流分别从70-140 mA (2-4 C)和3 5-105 mA (1-3 C)的范围内抽出(蓝色阴影区域)。如果在时间限制之前达到4.3 V的安全阈值电压，则停止充电。在放电过程中，随机在35-140 mA (1-4 C)范围内选择一个恒定的放电电流(红色阴影区域)，直到电压降至3.0 V。

Capacity forecasting using EIS

We first consider the setting in which we want to predict the next cycle discharge capacity, for a cell whose usage history (including for example, cycle or calendar age, or historical capacity–voltage data) is completely unknown, if we apply a particular charging and discharging profile. We frame the problem as a regression task, and train a probabilistic machine learning model to learn the mapping $Q_n=f(s_n,a_n)$, with uncertainty estimates, where $s_n$ is the battery state at the start of the nth cycle, an is the future action (the nth cycle charge/ discharge protocol), and Qn is the discharge capacity measured at the end of the cycle. The battery state vector sn is formed from the concatenation of the real （$Z_{re}$）and imaginary（$Z_{im}$ ) components of the impedance measured at 57 frequencies, ${\omega }_1，\dots {\omega }_{57}$, in the range 0.02Hz-20kHz;$s_n=[Z_{re}({\omega }_1),Z_{im}({\omega }_1),...,Z_{re}({\omega }_{57}),Z_{im}({\omega }_{57})]$. The action vector is formed from the concatenation of the nth cycle charge and discharge currents.

如果我们应用特定的充放电剖面，我们首先考虑我们想要预测下一个周期放电容量的设置，对于一个使用历史(例如，周期或日历年龄，或历史容量-电压数据)完全未知的电池。我们将问题框架为一个回归任务，并训练一个概率机器学习模型来学习映射$Q_n=f(s_n,a_n)$，具有不确定性估计，其中$s_n$是第$n$个循环开始时的电池状态，an是未来的动作(第n个循环充电/放电协议)，$Q_n$是循环结束时测量的放电容量。电池状态矢量$s_n$在57个频率下测量的阻抗的实（$Z_{re}$）和虚（$Z_{im}$）分量的串联形成，${\omega }_1，\dots {\omega }_{57}$，在0.02Hz-20kHz范围内;$s_n=[Z_{re}({\omega }_1),Z_{im}({\omega }_1),...,Z_{re}({\omega }_{57}),Z_{im}({\omega }_{57})]$。动作矢量由第n个循环充电和放电电流的串联形成。

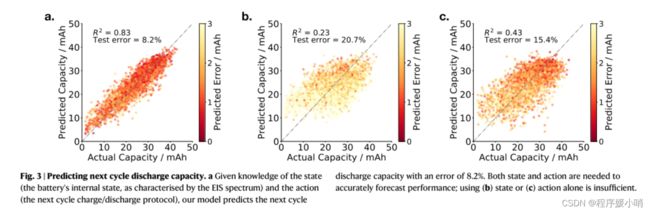
Figure 3 illustrates the accuracy of our model. Using both state and action as input, the next cycle discharge capacity is predicted with an average error of 8.2%. Importantly, both state and action (Fig. 3a) are found to be necessary to predict future cell performance: if state (Fig. 3b) or action (Fig. 3c) alone are used as inputs, the test error approximately doubles to 20.7% and 15.4% respectively. This demonstrates the importance of both the cell’s internal health and the externally selected usage in determining realised cell performance.

图3说明了我们模型的准确性。以状态和动作作为输入，预测下一循环放电容量，平均误差为8.2%。重要的是，状态和动作(图3a)都被发现是预测未来单元性能所必需的:如果仅使用状态(图3b)或动作(图3c)作为输入，测试误差大约翻倍，分别为20.7%和15.4%。这证明了电池的内部健康和外部选择的使用在决定实现电池性能方面的重要性。

For applications such as optimised charging and repurposing triaging, it is important that a model of battery life trajectory can forecast not only the immediate next cycle discharge capacity, but also capacity several cycles into the future49,50. With this in mind , we next investigate how the predictive accuracy of the model changes as we push the model to predict capacity further into the future. In each case, the input comprises the concatenation of the state representation at the start of the nth cycle, sn, with the ‘action’ vector an…n+j comprising all charging and discharging currents that will be applied between cycle n and cycle n + j

对于优化充电和再利用分类等应用，重要的是电池寿命轨迹模型不仅可以预测下一个循环的放电容量，而且可以预测未来几个循环的容量。考虑到这一点，我们接下来将研究模型的预测准确性如何变化，因为我们推动模型预测未来的容量。在每种情况下，输入包括第n个周期开始时的状态表示$s_n$与“动作”向量$a_{n\dots N+j}$包括在循环$n$和循环$n+j$之间应用的所有充电和放电电流

Figure 4 shows how the coefficient of determination $R^2$changes with j. As expected, the accuracy of the model generally decreases as the forecasting interval increases. However, the model still attains $R^2$= 0.75 when projecting 40 cycles into the future.

图4显示了决定系数$R^2$随$j$的变化情况。正如预期的那样，随着预测区间的增加，模型的精度一般会下降。然而，当预测未来40个周期时，模型仍然得到$R^2$ = 0.75。

Fig. 3 | Predicting next cycle discharge capacity. a Given knowledge of the state (the battery’s internal state, as characterised by the EIS spectrum) and the action (the next cycle charge/discharge protocol), our model predicts the next cycle discharge capacity with an error of 8.2%. Both state and action are needed to accurately forecast performance; using (b) state or ( c ) action alone is insufficient.

图3 |预测下一循环放电容量。a给定状态(电池的内部状态，由EIS谱表征)和动作(下一个循环充放电协议)的知识，我们的模型预测下一个循环放电容量的误差为8.2%。要准确预测业绩，既需要状态，也需要行动;仅使用(b)行为或( c )行为是不够的。

Fig. 4 | Multi-step forecasting. Our model can also forecast longer term battery performance, as quantified by (a) % test error, and (b) R2 value. Given the EIS spectrum and knowledge of the next protocols that will be applied to the cell, the discharge capacity is predicted with a test error of less than 10% up to 32 cycles in advance.

图4 |多步预测。我们的模型还可以预测电池的长期性能，通过(a) %测试误差和(b) R2值进行量化。考虑到EIS光谱和将应用于电池的下一个协议的知识，放电容量预测的测试误差小于10%，最多可提前32个周期。

Data efficiency and robustness to domain shift

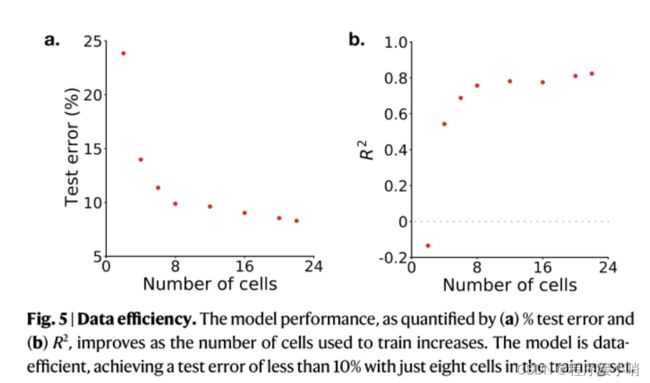
Fig. 5 | Data efficiency. The model performance, as quantified by (a) %test error and (b) R2, improves as the number of cells used to train increases. The model is dataefficient, achieving a test error of less than 10% with just eight cells in the training set.

图5 |数据效率。由(a) %测试误差和(b) R2量化的模型性能随着用于训练的细胞数量的增加而提高。该模型具有数据效率，在训练集中只有8个单元的情况下，测试误差小于10%。

We next test the robustness of our method by investigating data efficiency and model generalisability. To test data efficiency, we measure how performance changes as the number of cells used to train the model increases. As seen in Fig. 5, there is a marked reduction in test error from 23.8% to 8.2% as the number of cells increases from two to 22. Nevertheless, the model is demonstrably data-efficient, with just eight cells needed to obtain a test error of less than 10%.

接下来，我们通过调查数据效率和模型的可泛化性来测试我们方法的稳健性。为了测试数据效率，我们测量性能如何随着用于训练模型的单元数的增加而变化。如图5所示，随着单元数从2个增加到22个，测试误差从23.8%显著降低到8.2%。尽管如此，该模型证明是数据高效的，只需要8个单元就可以获得小于10%的测试误差。

An important test of model generalisability is to study model accuracy when the domain distribution changes, i.e. when the model is being deployed in settings that are different from the training data.

模型泛化性的一个重要测试是研究领域分布变化时的模型精度，即当模型部署在与训练数据不同的设置中时。

This is important for deployment in the field as the approach needs to be robust to driving patterns that might be different from the training data8. We test model robustness by cycling an additional 16 cells from the same manufacturer, but now adjusting the cycling protocol by fixing the discharge current to 1.5C for each cell throughout its life. We use a model trained using only cells that were subjected to random discharge currents over their lifetime, to predict next-cycle discharge capacity of cells subjected to fixed discharging. To illustrate the difference in training and test datasets, the distribution of discharge capacities is shown for each in Fig. 6a.
The predictive accuracy of the model on the fixed discharge dataset is illustrated in Fig. 6b. Promisingly, the model attains a test error of just 6.3% on this domain-shifted dataset, which corresponds to R2 = 0. 76 .

这对于现场部署非常重要，因为该方法需要对可能与训练数据不同的驾驶模式具有鲁棒性。我们通过循环来自同一制造商的另外16个电池来测试模型的稳健性，但现在通过在整个生命周期中将每个电池的放电电流固定在1.5C来调整循环协议。我们使用一个仅使用在其生命周期内受到随机放电电流的电池训练的模型，来预测受到固定放电的电池的下一个周期放电容量。为了说明训练数据集和测试数据集的差异，放电能力的分布如图6a所示。
模型在固定流量数据集上的预测精度如图6b所示。有希望的是，该模型在这个域移位数据集上的测试误差仅为6.3%，对应于$R^2$ = 0.76

Our model also outputs predictive uncertainty, which indicates how certain the model is about the quality of its predictions. It is especially important in the domain-shifted setting that the model ‘knows what it does not know’ and estimates high predictive uncertainty about data points that it is likely to obtain a high error on. We can test the model’s ability to estimate its uncertainty by observing how the average test error changes as the number of data points is reduced to include only the data points that the model is most confident about. If a model can successfully estimate its level of certainty, the average test error should reduce as the proportion of data is reduced to include only the most confidently predicted points. Figure 6c shows a 3 2 % reduction in root-mean-squared error (RMSE) as the proportion of data is reduced from 100% to the most confident 25%, demonstrating that our model has learnt which predictions it should be confident about.

我们的模型还输出预测不确定性，这表明模型对其预测质量的确定程度。在域移位的情况下，模型“知道它不知道的东西”并估计数据点的高度预测不确定性是特别重要的，它可能会在这些数据点上获得很高的误差。我们可以通过观察平均测试误差如何随着数据点数量的减少而变化来测试模型估计其不确定性的能力，以只包括模型最有信心的数据点。如果一个模型能够成功地估计其确定性水平，那么平均测试误差应该随着数据比例的减少而减少，只包括最自信的预测点。图6c显示，当数据比例从100%降低到最可信的25%时，均方根误差(RMSE)减少了3.2%，这表明我们的模型已经学会了它应该对哪些预测有信心。

Fig. 6 | Robustness to domain shift. a The distribution of discharge capacity is different for cells cycled under variable discharge rates (blue) compared to a fixed discharge rate (red); the overlap region of the two distributions appears darker in colour. b Our model, trained on the variable discharge rate cells, accurately predicts the discharge capacities of cells cycled under a fixed discharge rate. The colour of the plotted points denotes predicted uncertainty (see colour bar). c The model `knows what it does not know’: when we restrict the test data used to calculate the root-mean squared error (RMSE) by including only the predictions that the model is most confident about (i.e. with lowest predictive uncertainty), the RMSE reduces.

图6 |对域移位的鲁棒性。
a与固定放电率(红色)相比，在可变放电率(蓝色)下循环的细胞的放电容量分布是不同的;两个分布的重叠区域颜色较深。
b我们的模型在可变放电率单元上训练，准确地预测了在固定放电率下循环的单元的放电能力。标绘点的颜色表示预测的不确定性(见颜色条)。
c模型“知道它不知道的东西”:当我们限制用于计算均方根误差(RMSE)的测试数据，只包括模型最有信心的预测(即具有最低的预测不确定性)，RMSE会降低。

Comparison of state representation

Having demonstrated the ability of the EIS spectrum to capture battery state, we now benchmark this representation of battery health against other approaches utilised in the literature, including the state-of-the-art feature-based method22,51, and consider whether there are additional features to the EIS spectrum that can serve to augment battery state.

在演示了EIS光谱捕捉电池状态的能力后，我们现在将这种电池健康状况的表示与文献中使用的其他方法进行基准测试，包括最先进的基于特征的方法，并考虑EIS光谱是否有其他特征可以增强电池状态。

Simple measures that have been used to forecast or estimate battery SOH include using the previous cycle discharge capacity, or the capacity throughput since cycling commenced. More advanced approaches include extracting features of the historical capacity–voltage discharge curves, as shown in Fig. 1. The state-of-the-art approach to extracting such features was implemented by Severson et al22 and inspired the approaches to feature extraction used recently by Attia et al and Paulson et al37,51. We benchmark how our EIS-based approach performs relative to those state-of-the-art features.

用于预测或估计电池SOH的简单措施包括使用之前的循环放电容量，或循环开始后的容量吞吐量。更先进的方法包括提取历史容量-电压放电曲线的特征，如图1所示。提取这些特征的最先进的方法是由Severson等人实现的，而不是最近由Attia等人和Paulson等人使用的特征提取方法。我们对基于ais的方法相对于这些最先进的功能的性能进行基准测试。

Further, we assess whether incorporation of physical interpretations, in the form of equivalent circuit models (ECM), improves predictions. We use the widely implemented Randles circuit model, comprising a series resistance, connected with a resistance in parallel with a capacitance and a Warburg impedance element, as well as the more complex Extended Randles circuit, which adds an additional resistor-capacitor parallel combination in series to the Randles circuit.
The ECM is fitted to the spectrum (at an associated computational cost) and we use the extracted parameters as the state representation instead of raw EIS data.
In total, we consider the following features in our benchmark:

• Previous cycle discharge capacity $Q_{n-1}$.
• Capacity throughput (CT) since cycling commenced, as defined by the sum of cell charge and discharge capacities from cycles 0 to $n-1$.
• State of Health (SOH), as defined by $Q_{n-1}/Q_0$.
• State-of-the-art features of the capacity–voltage discharge curve (CVF): Following Severson et al, we form a state representation at the start of cycle n by extracting features from the capacity–voltage discharge curve after cycle n − 1. We fit e a c h curve to a spline function, linearly interpolating to measure capacity at 1000 evenly spaced voltages from $V_{m}in$ to $V_{m}ax$. T h i s 1000-dimensional capacity vector $Q_{n-1}$ is normalised by subtracting the equivalent vector from cycle 0, $Q_0$. The following features are then used as inputs: $V_{max}$, $V_{min}$, $log(var(Q_{n-1}-Q_0))$, $log(IQR(Q_{n-1}-Q_0))$. Additionally, we fit the capacity to a sigmoid$Q\left(\tilde{V}\right)=\frac{p_0}{1.0+\exp \left(p_1\left(V-p_2\right)\right)}$ where $\tilde{V}$ is the normalised voltage and use the parameters p0, p1, p2 as features.
• Equivalent circuit model parameters (ECM-R and ECM-ER): We fit equivalent circuit models using the Randles circuit (ECM-R) and Extended Randles circuit (ECM-ER) to the EIS spectra and concatenate the obtained parameters together.

此外，我们评估了以等效电路模型(ECM)的形式纳入物理解释是否能改善预测。我们使用广泛应用的兰德尔电路模型，包括一个串联电阻，与一个并联电容和一个Warburg阻抗元件的电阻连接，以及更复杂的扩展兰德尔电路，它在兰德尔电路中增加了一个额外的电阻-电容并联组合。
ECM拟合到频谱(在相关的计算成本下)，我们使用提取的参数作为状态表示，而不是原始EIS数据。
总的来说，我们在基准测试中考虑了以下特性:

• 前一循环放电容量$Q_{n-1}$。
• 自循环开始以来的容量吞吐量(CT)，由周期0到n−1的电池充放电容量之和定义。
• 运行状况(SOH)，定义为$Q_{n-1}/Q_0$。
• 容量-电压放电曲线(CVF)的最新特征:继Severson等人之后，我们通过从周期n−1后的容量-电压放电曲线中提取特征，在周期n开始时形成一个状态表示。我们拟合一个$c_h$曲线到一个样条函数，线性插值来测量1000个均匀间隔电压从$V_{min}$到$V_{max}$的容量。T h i的1000维容量向量Qn−1通过从周期0,Q0中减去等效向量进行归一化。然后使用以下特征作为输入:$V_{max}$, $V_{min}$, $log(var(Q_{n-1}-Q_0))$, $log(IQR(Q_{n-1}-Q_0))$.。此外，我们将容量拟合为一个$Q\left(\tilde{V}\right)=\frac{p_0}{1.0+\exp \left(p_1\left(V-p_2\right)\right)}$ ，其中$\tilde{V}$为归一化电压，并使用参数p0, p1, p2作为特征。
• 等效电路模型参数(ECM-R和ECM-ER):我们使用Randles电路(ECM-R)和Extended Randles电路(ECM-ER)拟合等效电路模型到EIS谱，并将得到的参数连接在一起。

We note that in contrast to EIS features, the formation of a state representation using the first four aforementioned features demands access to historical current-voltage data, over at least the entirety of the previous discharge and for some features, over the entire cell lifetime. However, they benefit from the advantage of not requiring equipment to measure the EIS spectrum, which comes with an associated financial and temporal cost. Forming a state representation using the ECM parameters (extracted from the EIS spectrum) has an associated computational cost and can be considered a form of dimensionality reduction of the raw EIS data. An additional problem faced by ECMs in general is non-uniqueness, in that multiple different combinations of ECM parameters can generally explain a particular EIS spectrum equally well52.

我们注意到，与EIS特征相比，使用前面提到的前四个特征形成的状态表示需要访问历史电流-电压数据，至少在之前的整个放电过程中，对于某些特征，在整个电池寿命中。然而，他们受益于不需要设备来测量EIS光谱的优势，这带来了相关的财务和时间成本。使用ECM参数(从EIS谱中提取)形成状态表示具有相关的计算成本，可以认为是原始EIS数据降维的一种形式。ECM通常面临的另一个问题是非唯一性，因为ECM参数的多个不同组合通常可以同样好地解释特定的EIS谱。

Table 1 shows how the state representation impacts test error and model goodness of fit. In all cases, the model is trained to predict the next cycle discharge capacity, given the next cycle protocol and the chosen state representation. Interrogating the relative importance of features, we first consider the baseline of using EIS only (without including the protocol) and using the protocol only (without including EIS). Perhaps unsurprisingly, battery degradation is a function of both the current state and future charge/discharge protocol. As such, using both EIS and the protocol significantly outperforms using EIS only or using the protocol only.

表1显示了状态表示对测试误差和模型拟合优度的影响。在所有情况下，训练模型预测下一个周期放电容量，给定下一个周期协议和选择的状态表示。在询问特性的相对重要性时，我们首先考虑只使用EIS(不包括协议)和只使用协议(不包括EIS)的基线。也许不出意外，电池的退化是当前状态和未来充放电协议的一个函数。因此，同时使用EIS和协议的性能明显优于仅使用EIS或仅使用协议的性能。

We then explore the impact of physics-based representation of the EIS spectrum, using the Randles (ECM-R) and extended Randles (ECM-ER) equivalent circuit models. Comparing EIS + Protocol with ECM-R + Protocol and ECM-ER + Protocol reveals that these physicsbased models lose information, and using a machine learning approach to directly learn from raw data might be advantageous.

然后，我们使用兰德尔(ECM-R)和扩展兰德尔(ECM-ER)等效电路模型，探讨了基于物理的EIS频谱表示的影响。EIS +Protocol与ECM-R +Protocol和ECM-ER +Protocol的比较表明，这些基于物理的模型会丢失信息，使用机器学习方法直接从原始数据中学习可能是有利的。

We next consider the different approaches that have been reported in the literature, Qn−1, SOH, CT, and CVF, with CVF being the state-of-the-art in the battery informatics literature. In all cases, EIS + Protocol outperforms those other features with Protocol, although CVF is competitive.

接下来，我们考虑文献中报道的不同方法，Qn−1,SOH, CT和CVF，其中CVF是电池信息学文献中最先进的方法。在所有情况下，EIS +Protocol优于Protocol的其他特性，尽管CVF具有竞争力。

Interestingly, information from capacity–voltage curve data (CVF) is complementary to EIS - combining EIS with these features leads to a significant increase in accuracy (EIS + CVF + Protocol). This is perhaps unsurprising, as EIS probes the impedance of the single ‘static’ cell discharged state (with high information content per instant state), whilst capacity–voltage curves probe how the cell state evolves continuously over the path from charged to discharged (with low information content per instant state).

Finally, the best model performance is attained by combining all of the above features to form the state representation. In this case the average test error is just 6.2%.

有趣的是，来自容量-电压曲线数据(CVF)的信息是EIS的补充-将EIS与这些特征结合起来会显著提高准确性(EIS + CVF +Protocol)。这也许并不令人惊讶，因为EIS探测单个“静态”电池放电状态的阻抗(每个瞬间状态具有高信息含量)，而容量-电压曲线探测电池状态如何在从充电到放电的路径上连续演变(每个瞬间状态具有低信息含量)。

最后，通过结合上述所有特征来形成状态表示，从而获得最佳的模型性能。在这种情况下，平均测试误差仅为6.2%。

Robustness to different cell manufacturers

We now extend our analysis to explore how robust our approach is to changing the cell manufacturer, adjusting the operating temperature and adjusting the average use pattern. We repeat our experiment on a new batch of 32 commercial LiR coin cells (of nominal capacity 1 C = 40 mAh) from RS Pro, a different manufacturer, except we now make the problem significantly more challenging by subjecting different subgroups of cells to one of four different usage distributions. These usage distributions are shown in Supplementary Table 1.

我们现在扩展我们的分析，以探索我们的方法在改变电池制造商、调整操作温度和调整平均使用模式方面的鲁棒性。我们在另一家制造商RS Pro的新一批32块商业锂离子可充电纽扣电池(标称容量为1 C = 40 mAh)上重复了我们的实验，只是我们现在让问题变得更具挑战性，让不同的电池亚组分别接受四种不同的使用分布中的一种。这些使用情况的分布见补充表1。

We measure the accuracy of the model in two ways: firstly, we consider the case where the model is exposed to cells that have been subjected to the same distribution of protocols as the test set (random splitting), and second, the more challenging case where the model is only trained on the cells which are subjected to three of the cycling protocol distributions and tested on the remaining eight cells subjected to a different cycling protocol. This is a much harder task as the average usage on the test cells is very different to the average usage on the training cells—it is a test of whether the model can extrapolate to different average use not just different cycle-to-cycle use.

我们通过两种方式来衡量模型的准确性:
首先，我们考虑模型暴露于与测试集受到相同协议分布(随机分裂)的锂电池单体的情况，
其次，更具有挑战性的情况，即模型只在受到三种循环协议分布的锂电池单体上训练，并在受到不同循环协议的其余八个锂电池单体上测试。
这是一项更加艰巨的任务，因为测试单元格上的平均使用量与训练单元格上的平均使用量非常不同——这是一个测试模型是否可以外推到不同的平均使用量，而不仅仅是不同的周期到周期的使用。

The results for different state representations are shown in Table 2 for both the case where the train/test split is random, and where the split is stratified into different usage patterns. Comparable observations are made for cells purchased from the second manufacturer: namely, the most accurate predictions are made when the state representation is formed using features of the EIS spectrum alongside those formed from the discharge curve (CVF). As expected, the model performs significantly better when it has been trained on data from some cells that have been exposed to a similar distribution of cycling patterns as those that the model is tested on. However, the model remains performant in the scaffold split scenario, and in this setting the test error reduces by 30% when the state representation is formed using the EIS spectrum alongside the features of the discharge curve, instead of solely using features of the discharge curve.

表2显示了不同状态表示的结果，其中训练/测试分割是随机的，以及分割分层为不同的使用模式。对从第二个制造商购买的电池进行了比较观察:即，当使用EIS谱的特征与放电曲线(CVF)形成的特征形成状态表示时，进行了最准确的预测。
正如预期的那样，当它使用来自一些锂电池单体的数据进行训练时，模型的表现明显更好，这些锂电池单体暴露在与模型测试时相似的循环模式分布中。
然而，该模型在支架分裂场景中仍然具有性能，在这种设置下，当使用EIS谱和放电曲线的特征而不是单独使用放电曲线的特征来形成状态表示时，测试误差降低了30%。

These additional results further demonstrate that if available, both the EIS spectrum and discharge curve can act as informative markers of the battery’s internal state, but that they are complementary to each other.

We next verify that the model is robust with respect to changing external operating temperature. We cycle an additional 16 cells at 35 °C and test the model trained on data from cells cycled at room temperature. Table 3 shows that our model can extrapolate to cells operated at these higher temperatures, but that the EIS spectrum plays a particularly important role in characterising the battery state when the cell is not operated at the same temperature. The model obtains a test error of 34.2% when only the discharge curve features are used to characterise state, which reduces to 14.0% when both the EIS spectrum and discharge curve features are used. This further demonstrates the additional information that EIS signals contain relative to chargingdischarging curves, and supports the hypothesis that EIS implicitly tracks temperature53.

这些额外的结果进一步证明，如果可用，EIS谱和放电曲线都可以作为电池内部状态的信息标记，但它们是相互补充的。
接下来，我们验证该模型对于外部操作温度的变化是稳健的。我们在35°C下循环另外16个锂电池单体，并在室温下循环的锂电池单体数据上测试训练的模型。
表3显示，我们的模型可以外推到在这些更高温度下工作的电池，但当电池不在相同温度下工作时，EIS谱在表征电池状态方面起着特别重要的作用。仅使用放电曲线特征表征状态时，模型的测试误差为34.2%，同时使用EIS谱和放电曲线特征时，模型的测试误差为14.0%。这进一步证明了EIS信号相对于充放电曲线所包含的额外信息，并支持了EIS隐式跟踪温度的假设。

We make qualitatively similar observations when we test our approach on cells manufactured by RS Pro (rather than Powerstream), with EIS found to be a slightly better state representation than state-of-the-art capacity-voltage features (CVF). The best results are obtained when the two representations are combined. We test how the model performs when we split the training and testing sets randomly, and when we instead stratify the training and testing sets such that the model is tested on cells with a different usage distribution to the cells it was trained on. Usage conditions and an extended comparison of different state representations are provided in Supplementary Tables 1, 2 and 3.

当我们在RS Pro(而不是Powerstream)制造的电池上测试我们的方法时，我们得到了质的相似的观察结果，发现EIS比最先进的容量电压特征(CVF)的状态表示略好。
将两种表示法结合起来可以得到最好的结果。当我们随机分割训练集和测试集时，当我们对训练集和测试集进行分层时，我们会测试模型的表现，这样模型就会在与它所训练的细胞具有不同使用分布的细胞上进行测试。
在补充表1、2和3中提供了使用条件和不同状态表示的扩展比较。

Discussion

In this paper, we showed that the electrochemical impedance spectrum accurately characterises the internal state of a cell, and a machine learning model can be trained to accurately forecast both immediate and longer term cell performance with predictive uncertainty, even amid uneven and unknown historical cell usage. Our model achieves comparable accuracy (8.2% test error) to the state-of-the-art forecasting approach (8.8% test error) when testing on cells subjected to the same distribution of operating conditions as the cells used to train the model. However, as outlined in Fig. 1, the state-of-the-art approach demands access to historical cycling data whereas our model enables forecasting with no historical data. Additionally, our model significantly outperforms the state-of-the-art model when extrapolating to a higher operating temperature, with a 57% reduction in test error (from 34.2% to 14.6%).

在本文中，我们展示了电化学阻抗谱准确地表征了电池的内部状态，并且可以训练机器学习模型，即使在不均匀和未知的历史电池使用情况下，也可以准确地预测短期和长期电池性能。我们的模型达到了与最先进的预测方法(8.2%的测试误差)相当的准确性(8.8%的测试误差)，当测试单元受到相同的操作条件分布时，用于训练模型的单元。

然而，如图1所示，最先进的方法需要访问历史循环数据，而我们的模型可以在没有历史数据的情况下进行预测。此外，当外推到更高的工作温度时，我们的模型显著优于最先进的模型，测试误差降低了57%(从34.2%降至14.6%)。

Our method is data-efficient, achieving a next-cycle test error of 9.9% with training data from just eight cells, and is robust to shifts in dataset distributions. Additionally, we find that there is scope to boost model performance by 25% if historical cycling data is available; such data can be used to derive features that augment the cell state representation. We demonstrate that our approach can be utilised across different cell chemistries, and the model is robust to different operating temperatures.

我们的方法是数据高效的，仅使用八个单元的训练数据就实现了9.9%的下一个周期测试误差，并且对数据集分布的变化具有鲁棒性。
此外，我们发现，如果历史循环数据可用，则有空间将模型性能提高25%; 这样的数据可用于派生增强单元状态表示的特征。我们证明了我们的方法可以用于不同的电池化学成分，并且该模型对不同的操作温度具有鲁棒性。

Our approach differentiates from the prior art in two important ways : First, we employ an information-rich electrical signal—EIS— which captures the response of the cell across different timescales without any knowledge of the cycling history. This is in contrast to most existing methods which employ features from the charging–discharging curve—a s i g n ificantly more coarse-grained signal—as input to machine learning models. Our results suggest significant improvements in battery management systems abound by incorporating circuitries that measure electrochemical impedance, albeit at a financial and temporal cost.

我们的方法在两个重要方面与现有技术不同:
首先，我们采用了信息丰富的电信号- eis -它在不了解周期历史的情况下捕捉锂电池单体在不同时间尺度上的响应。
这与大多数现有的方法形成了对比，这些方法使用来自充放电曲线的特征——一种明显更粗粒度的信号——作为机器学习模型的输入。
我们的研究结果表明，通过整合测量电化学阻抗的电路，电池管理系统有了显著的改进，尽管在财务和时间上都有成本。

Second, we focus on uneven cycling, where the charging and discharging rates vary from cycle to cycle. This departs from previous studies on machine learning for battery degradation which focused on constant charge/discharge conditions, which are typical in battery testing. Our results problematise the concept of a single scalar State of Health, as the state of the battery is dependent on the extent of the myriad different degradation mechanisms, which in turn depends on the sequence of historic charge/discharge protocols. Rather, we suggest that a cell can be described by a multidimensional state vector, captured using informative high-dimensional measurements like EIS, and a machine learning approach can be used to predict future capacities given the state vector and future charge/discharge protocols.

其次，我们关注不均匀循环，其中充放电速率随循环而变化。这与之前关于电池退化的机器学习的研究不同，以前的研究集中在恒定的充放电条件下，这是电池测试中的典型情况。我们的结果对单一标量健康状态的概念提出了质疑，因为电池的状态取决于无数不同退化机制的程度，而这又取决于历史充放电协议的顺序。相反，我们建议电池可以用多维状态向量来描述，使用信息性高维测量(如EIS)来捕获，并且可以使用机器学习方法来预测给定状态向量和未来充电/放电协议的未来容量。

Furthermore, although in this work we only consider forecasting starting from an initially discharged state, we hypothesise that it should be possible in future work to forecast discharge capacity starting from any state of charge based on the EIS measurement, since EIS spectrum implicitly tracks state of charge.

此外，尽管在这项工作中，我们只考虑从初始放电状态开始预测，但我们假设，在未来的工作中，应该有可能根据EIS测量从任何电荷状态开始预测放电容量，因为EIS谱隐含地跟踪电荷状态。

We note that the general framework that we have laid out for predicting future battery performance given current cell state and future actions has scope to be applied in a broad range of battery diagnostic and control settings. For example, predicting the effect of a proposed charging protocol on next cycle discharge capacity as well as long term degradation is important for optimising rapid charging applications51, where a balance must be achieved between charging time and rate of cell degradation. Our work can additionally be extended to consider more complicated dynamic usage protocols, such as WLTC

我们注意到，鉴于当前电池状态和未来行动，我们为预测未来电池性能所制定的总体框架，在广泛的电池诊断和控制设置中具有应用范围。例如，预测所提议的充电协议对下一个周期放电容量以及长期退化的影响对于优化快速充电应用是重要的，其中必须在充电时间和电池退化率之间实现平衡。我们的工作还可以扩展到考虑更复杂的动态使用协议，比如WLTC

Methods

Battery cycling

For this study we cycle 88 commercial LiR coin cells purchased from two different manufacturers, Powerstream and RS Pro, in a temperature regulated laboratory at 23 ± 2 °C. A Biologic BCS-805 potentiostat is used for cycling, and photographs of the experimental setup are provided in Supplementary Fig. 2.

Across all datasets, cells are subjected to a sequence of randomly selected charge and discharge currents for 110–120 full charge/discharge cycles. Cycling commences when the cell is in the fully discharged state, and each cycle comprises the following steps: (a) resting for 20 min at the open circuit voltage, (b) acquisition of the galvanostatic EIS spectrum in the fully discharged state, © two stage CC charging, (d) resting for 20 min at the open circuit voltage, (e) acquisition of the galvanostatic EIS spectrum in the fully charged state, (f) one stage CC discharging. The galvanostatic EIS spectrum is always measured by collecting impedance measurements at 57 frequencies uniformly distributed in the log domain in the range 0.02Hz-20kHz using a sinusoidal current with amplitude of 5 mA. Cells are cycled in a temperature-controlled lab room at 23 ± 2 °C.

To generate the first dataset, we cycle 24 Powerstream LiR 2032 coin cells (nominal capacity 1 C = 35 mAh). For these cells, charging consists of a two-stage CC protocol; currents are randomly selected in the ranges 70–140mA (2C–4C) and 35mA-105mA (1C-3C) in stages 1 and 2 respectively. A time limit of 15 min is set for each charging stage such that the total charging time is constrained to be 30 min or less.

Charging will stop before the 30 min time limit if the safety threshold voltage of 4.3 V is reached. During discharging, a single constant discharge current, randomly selected in the range 35mA-140mA (1C–4C), is applied, until the voltage drops to 3.0 V.

An additional 16 cells (also manufactured by Powerstream and of nominal capacity 35 mAh) are cycled under the same conditions, except now we fix the discharge current at 52.5 mA (1.5C) for all cells and cycles, instead of randomly changing the discharge current at each cycle.

We then generate a second dataset that enables exploration of the model’s robustness to cell manufacturer, changes to usage pattern and operating temperature. We cycle 48 cells from a second manufacturer, RS Pro (nominal capacity 40 mAh), under a much wider range of usage patterns. The general six-step cycling protocol remains the same as described above, with each cell again being subjected to 100 cycles of two-stage CC charging, and one-stage CC discharging, with the three rates randomly selected at the start of each cycle. However, the distribution of currents now changes for each cell. Of these cells, sixteen are also cycled at a higher operating temperature of 35 ± 2 °C, in a temperature-controlled heating chamber. A description of the full set of operating conditions that each cell is subjected to is detailed in Supplementary Table 1.

在这项研究中，我们从两家不同的制造商Powerstream和RS Pro购买了88个商业LiR纽扣电池，在23±2°C的温度调节实验室中循环。使用Biologic BCS-805恒电位器进行循环，实验装置的照片见补充图2。

在所有数据集中，电池都受到一系列随机选择的充放电电流，进行110-120个完整的充放电周期。当电池处于完全放电状态时开始循环，每个循环包括以下步骤:(a)在开路电压下静置20分钟，(b)在完全放电状态下获得恒流EIS谱，©两级CC充电，(d)在开路电压下静置20分钟，(e)在完全充电状态下获得恒流EIS谱，(f)一级CC放电。恒流EIS谱总是通过收集均匀分布在0.02Hz-20kHz范围内的对数域57个频率的阻抗测量值，使用振幅为5 mA的正弦电流来测量。锂电池单体在温度控制在23±2°C的实验室中循环。

为了生成第一个数据集，我们循环24个Powerstream LiR 2032硬币电池(标称容量1 C = 35 mAh)。对于这些电池，充电包括两个阶段的CC协议;电流分别随机选择在70-140mA (2C-4C)和35mA-105mA (1C-3C)范围内的阶段1和阶段2。每个充电阶段设置15分钟的时间限制，使总充电时间限制在30分钟或更短。

如果达到4.3 V的安全阈值电压，将在30分钟时限前停止充电。在放电过程中，在35mA-140mA (1C-4C)范围内随机选择一个恒定的放电电流，直到电压降至3.0 V。

另外16个电池(也由Powerstream制造，标称容量为35毫安时)在相同的条件下循环，除了现在我们将所有电池和周期的放电电流固定在52.5 mA (1.5C)，而不是在每个周期随机改变放电电流。

然后，我们生成第二个数据集，以探索模型对电池制造商的鲁棒性、使用模式的变化和操作温度。我们从第二个制造商RS Pro(标称容量40毫安时)循环48个电池，在更广泛的使用模式下。一般的六步循环方案与上述相同，每个电池再次受到100个两阶段CC充电和一阶段CC放电的循环，在每个周期开始时随机选择三个速率。然而，电流的分布现在改变了每个单元。在这些电池中，有16个也在温度控制的加热室中，在35±2°C的较高操作温度下循环。补充表1详细描述了每个单元所承受的全套操作条件。

Machine learning model

All problems in this study are framed as regression tasks. We train a probabilistic machine learning model to learn the mapping $Q_j=f(s_n,a_{n\dots j})$, with uncertainty estimates, where sn is the battery state at the start of the nth cycle, an is the set of future cycling protocols applied over cycles n to j, a n d Qj is the discharge capacity at the end of the jth cycle. The battery state vector sn is formed from the concatenation of the real （$Z_{re}$）and imaginary（$Z_{im}$ ) components of the impedance measured at 57 frequencies, ${\omega }_1，\dots {\omega }_{57}$, in the range 0.02Hz-20kHz;$s_n=[Z_{re}({\omega }_1),Z_{im}({\omega }_1),...,Z_{re}({\omega }_{57}),Z_{im}({\omega }_{57})]$… For the task of predicting next cycle discharge capacity, the action vector an is formed from the concatenation of the nth cycle charge and discharge currents. When predicting discharge capacity several cycles, j, ahead of time, the future protocol is now formed from all charging and discharging currents that will be applied between cycle n and cycle n + j.

For the machine learning model, we use an ensemble of 10 XGBoost models58, each with 500 estimators and a maximum depth of 100. The mean and standard deviation of the predictions made by each model in the ensemble are used to quantify the predicted output and the predictive uncertainty. To test model performance we use the median R2 score and median percentage error. To obtain test metrics from a dataset comprising N cells, we randomly leave two test cells out, train on the remaining N−2 cells and repeat this process N/2 times, leaving different cells out each time.

本研究中的所有问题都被框定为回归任务。我们训练一个概率机器学习模型来学习映射$Q_j=f(s_n,a_{n\dots j})$，具有不确定性估计，其中$s_n$是第n个循环开始时的电池状态，$a_n$是应用于第n到第j个循环的未来循环协议集， $Q_j$是第j个循环结束时的放电容量。电池状态矢量$s_n$在57个频率下测量的阻抗的实（$Z_{re}$）和虚（$Z_{im}$）分量的串联形成，${\omega }_1，\dots {\omega }_{57}$，在0.02Hz-20kHz范围内;$s_n=[Z_{re}({\omega }_1),Z_{im}({\omega }_1),...,Z_{re}({\omega }_{57}),Z_{im}({\omega }_{57})]$。动作矢量由第n个循环充电和放电电流的串联形成。当预测几个周期$j$的放电容量时，未来的协议现在由在周期n和周期n + j之间应用的所有充电和放电电流形成。

对于机器学习模型，我们使用10个XGBoost模型的集成，每个模型有500个估计器，最大深度为100。集合中每个模型所作预测的平均值和标准差用于量化预测输出和预测不确定性。为了测试模型性能，我们使用中位数$R^2$分数和中位数百分比误差。为了从包含N个单元的数据集中获得测试指标，我们随机留出两个测试单元，在剩余的$N-2$个单元上进行训练，并重复此过程$N/2$次，每次留出不同的单元。

Data availability The data generated in this study are provided in the Zenobo database at https://doi.org/10.5281/zenodo.6645536.

Code availability The code required to reproduce this manuscript is available at https://github.com/PenelopeJones/battery-forecasting.