9.10 力扣669. 修剪二叉搜索树

669. 修剪二叉搜索树 - 力扣（LeetCode）

 

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 

所以结果应当返回修剪好的二叉搜索树的新的根节点。

注意：根节点可能会根据给定的边界发生改变。又因题目给出答案唯一。

示例 1：

输入：root = [1,0,2], low = 1, high = 2

输出：[1,null,2]

示例 2：

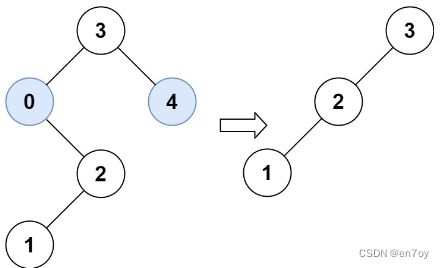
 输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3

 输出：[3,2,null,1]

思路：此树为一个二叉搜索树，在原有的根节点进行修剪，首先根节点不一定是返回时的根节点（root->val可能不符合条件），又题目给出答案会唯一，这里先找到符合条件的“根节点”。一个节点会被裁剪的情况只有两种：1.自身小于low2.自身大于high，此时处理方式分别为1.用右孩子代替自己2.用左孩子代替自己。处理完本身再继续判断左右孩子是否要裁剪。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* dfs(TreeNode* root,int low,int high)
    {
        //前序遍历
        if(root==nullptr) return root;
        //根的val会小于low，则dfs找right返回
        if(root->valright,low,high);
        //根的val会大于high，则dfs找left返回
        if(root->val>high) return dfs(root->left,low,high);
        root->left=dfs(root->left,low,high);
        root->right=dfs(root->right,low,high);
        return root;
    }
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root==nullptr) return root;
        TreeNode* ret=root;
        //找到返回的根节点
        while(ret!=nullptr&&(ret->valval>high))
        {
            if(ret->valright;
            else ret=ret->left;
        }
        ret=dfs(ret,low,high);
        return ret;
    }
};

方法二：迭代

思路：

如果一个结点 node 符合要求，即它的值位于区间 [low,high]，那么它的左子树与右子树应该如何修剪？

我们先讨论左子树的修剪：

node 的左结点为空结点：不需要修剪

node 的左结点非空：

1.如果它的左结点left 的值小于 low，那么 left 以及 left 的左子树都不符合要求，我们将 node 的左结点设为 \textit{left}left 的右结点，然后再重新对node 的左子树进行修剪。

2.如果它的左结点 left 的值大于等于low，又因为 node 的值已经符合要求，所以 left 的右子树一定符合要求。基于此，我们只需要对 left 的左子树进行修剪。我们令node 等于 left ，然后再重新对node 的左子树进行修剪。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        while (root && (root->val < low || root->val > high)) {
            if (root->val < low) {
                root = root->right;
            } else {
                root = root->left;
            }
        }
        if (root == nullptr) {
            return nullptr;
        }
        for (auto node = root; node->left; ) {
            if (node->left->val < low) {
                node->left = node->left->right;
            } else {
                node = node->left;
            }
        }
        for (auto node = root; node->right; ) {
            if (node->right->val > high) {
                node->right = node->right->left;
            } else {
                node = node->right;
            }
        }
        return root;
    }
};