代码随想录算法训练营第2天 |977.有序数组的平方 ，209.长度最小的子数组 ，59.螺旋矩阵
目录
977.有序数组的平方
解题思路
遇到的问题
实现代码
题目总结
209.长度最小的子数组
解题思路
遇到的问题
实现代码
题目总结
59.螺旋矩阵
解题思路
遇到的问题
实现代码
题目总结
今日心得
977.有序数组的平方
题目链接：977.有序数组的平方
给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。
示例 1：
- 输入：nums = [-4,-1,0,3,10]
- 输出：[0,1,9,16,100]
- 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]
示例 2：
- 输入：nums = [-7,-3,2,3,11]
- 输出：[4,9,9,49,121]
解题思路
考虑到数组中的元素有负数存在的问题，先对数组元素分别做平方处理，之后对数组元素进行排序。
1.暴力解法：
遍历数组中的元素，求每个元素的平方，之后对数组用sort()排序。
时间复杂度是 O(n + nlogn)
2.双指针
数组其实是有序的， 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。
此时可以考虑双指针法了，i指向起始位置，j指向终止位置。
定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
从后往前记录，将最大的写在最后面。
时间复杂度是 O(n)
遇到的问题
使用双指针法的时候，没有重新定义新数组的j，导致和原数组的r混淆。
实现代码
暴力解法：
class Solution {
public int[] sortedSquares(int[] nums) {
int n=nums.length;
int[] result=new int[n];
for(int i=0;i双指针法：
class Solution {
public int[] sortedSquares(int[] nums) {
int n=nums.length;
int l=0;
int r=n-1;
int [] res =new int[n];
int j=n-1;
while(l<=r){
if(nums[l]*nums[l]>nums[r]*nums[r]){
res[j]=nums[l]*nums[l];
j--;
l++;
}else{
res[j]=nums[r]*nums[r];
j--;
r--;
}
}
return res;
}
}题目总结
使用双指针法，i 指向起始位置，j 指向终止位置。
定义一个新数组 result，和 nums 数组一样的大小，让 k 指向 result 数组终止位置。
209.长度最小的子数组
题目链接： 209.长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
示例：
- 输入：s = 7, nums = [2,3,1,2,4,3]
- 输出：2
- 解释：子数组 [4,3] 是该条件下的长度最小的子数组。
提示：
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
解题思路
先找出和>=s的子数组，再对子数组的长度进行比较。
1.暴力解法：
两个for循环，然后不断的寻找符合条件的子序列，时间复杂度是O(n^2)。
2.滑动窗口：
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。时间复杂度O(n)。
遇到的问题
int sum =0应该写在两层for循环中，而不是循环外，因为每次循环都要将sum的值初始化为0，重新计算。
误把Math.min()写成了Math.max(),要多注意细节。
实现代码
暴力解法：
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//暴力
int n=nums.length;
int res=Integer.MAX_VALUE;
for(int i=0;i=target){
res=Math.min(j-i+1,res);
break;
}
}
}
return res==Integer.MAX_VALUE?0:res;
}
} 滑动窗口：
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//滑动窗口
int n=nums.length;
int l=0;
int res=Integer.MAX_VALUE;
int sum=0;
for(int r=0;r=target){
res=Math.min(r-l+1,res);
sum-=nums[l];
l++;
}
}
return res==Integer.MAX_VALUE?0:res;
}
} 题目总结
滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
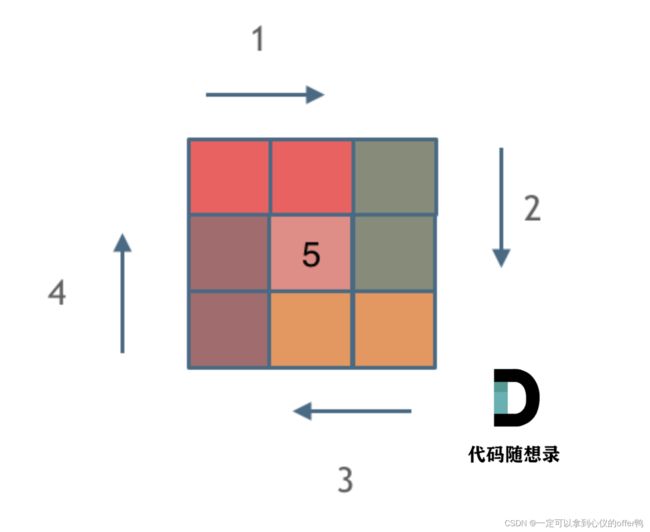
59.螺旋矩阵
题目链接：59.螺旋矩阵
给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
解题思路
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
- 要注意边界关系的处理问题，要始终保持一致，左开右闭or左闭右开。
遇到的问题
没有理解while（loop++ 改成正常的while（loop 代码随想录版： 其他版： 题目不是很复杂，但是还是挺绕的，边界信息要关注到。感觉先定义出四个边的信息，思路会更加清晰。 打卡的第二天啦~感觉写博客还是蛮耗费时间的，但是可以把自己的思路整理一下，也是不错的，希望自己可以坚持下去吧！实现代码
class Solution {
public int[][] generateMatrix(int n) {
int loop = 0; // 控制循环次数
int[][] res = new int[n][n];
int start = 0; // 每次循环的开始点(start, start)
int count = 1; // 定义填充数字
int i, j;
while (loop< n / 2) { // 判断边界后，loop从1开始
// 模拟上侧从左到右
for (j = start; j < n - loop-1; j++) {
res[start][j] = count++;
}
// 模拟右侧从上到下
for (i = start; i < n - loop-1; i++) {
res[i][j] = count++;
}
// 模拟下侧从右到左
for (; j > loop; j--) {
res[i][j] = count++;
}
// 模拟左侧从下到上
for (; i > loop; i--) {
res[i][j] = count++;
}
start++;
loop++;
}
if (n % 2 == 1) {
res[start][start] = count;
}
return res;
}
}
class Solution {
public int[][] generateMatrix(int n) {
int l=0,r=n-1,t=0,b=n-1;
int [][] res =new int [n][n];
int count =1,tar=n*n;
while(count<=tar){
for(int i=l;i<=r;i++){
res[t][i]=count++;// left to right.
}
t++;
for(int i=t;i<=b;i++){
res[i][r]=count++;// top to bottom.
}
r--;
for(int i=r;i>=l;i--){
res[b][i]=count++;// right to left.
}
b--;
for(int i=b;i>=t;i--){
res[i][l]=count++;// bottom to top.
}
l++;
}
return res;
}
}题目总结
今日心得