数据结构：图详解

图的存储方式

邻接矩阵

首先先创建图，这一个我们可以使用邻接矩阵或者邻接链
表来进行存储，我们要实现的无向图的创建，我们先创建
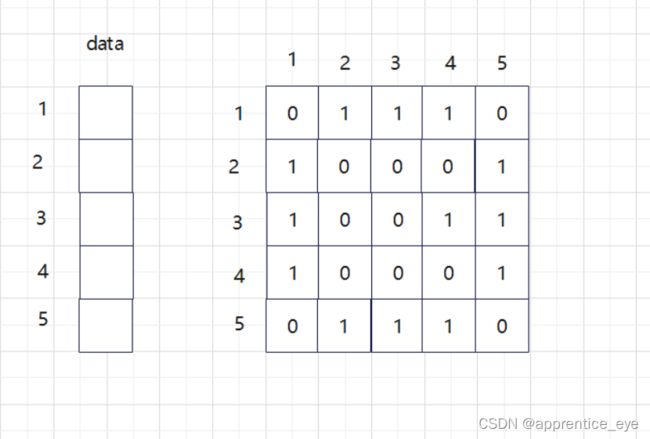
一个矩阵尺寸为n*n，n为图中的节点个数如图所示

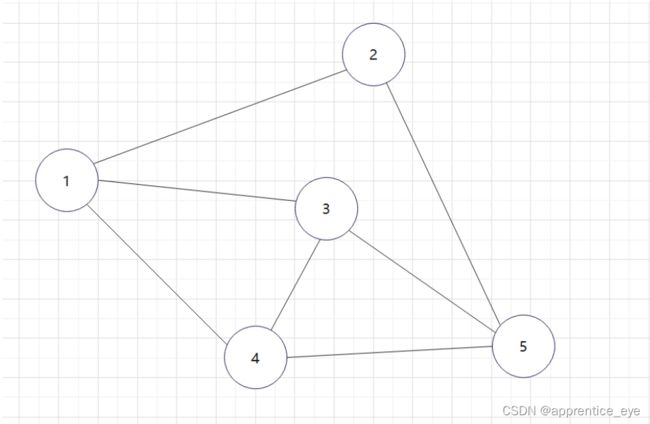
可以看出图中有5个结点，那我们创建的邻接矩阵的大小
就是5*5大小的

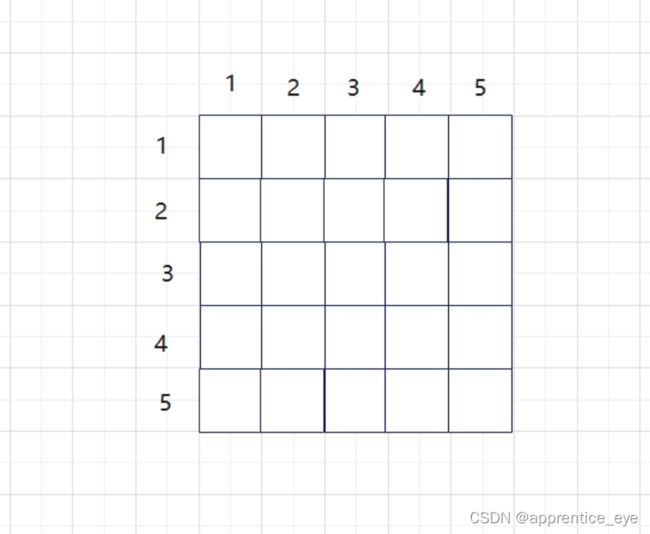
其中第一行就是存储的结点1与其他各个结点的关系，因
为我们建立的是无权图，所以对于两个结点之间有边我们
就存储1，无边就存储0。则上述图的邻接矩阵可以表示为

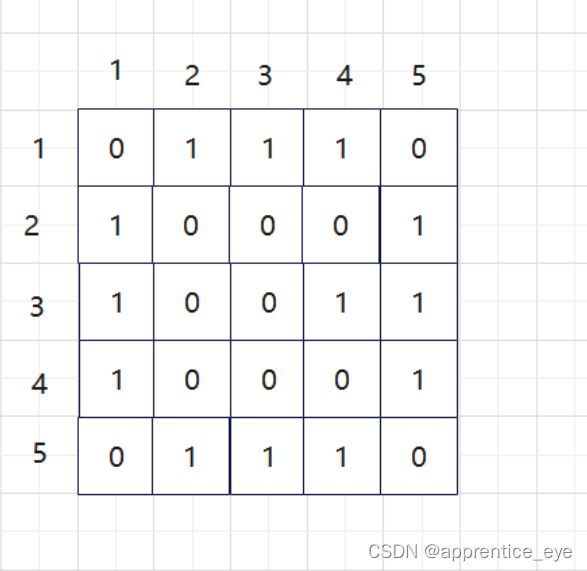
邻接矩阵表示了图中结点之间是否有边相连，并没有存储
结点的信息，所以我们还需要一个长为n的数组进行结点
信息的存储。
则邻接矩阵的完整表示如下：

邻接链表

我们可以看出在邻接矩阵中我们储存了任意两个结点的关系
无论它们是否有边相连，我们都把这个信息进行存储了，
但是这是不必要的，所以我们可以仅存储两个结点有边相连才进行存储，
这样就可以节省一部分不必要的空间。
对于上述图，我们要是使用邻接链表方法存储边的信息我们需要保留哪些信息呢？我们看一下，首先在邻接矩阵中为1的元素都代表这是一条边，但是1是一个标志，位置信息是隐含的，如果用邻接链表的话这种隐含的位置信息是没有的，如下图所示，我们只需要存储红色的信息

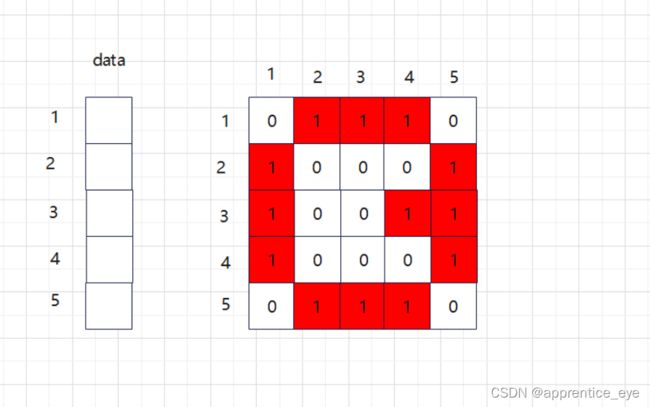
但是这些信息如果我们仍然存储0或1这是没有意义的，因为在邻接矩阵中位置信息是隐含的，而在邻接链表中没有隐含位置信息，所以不能用标志来标记是否存在此边，而应该存储实际存在的边的位置，因为起点是已知的，所以我们只需要在邻接链表中存储终点位置就行了，那么上面图的邻接矩阵转换为邻接链表就可以表示为：

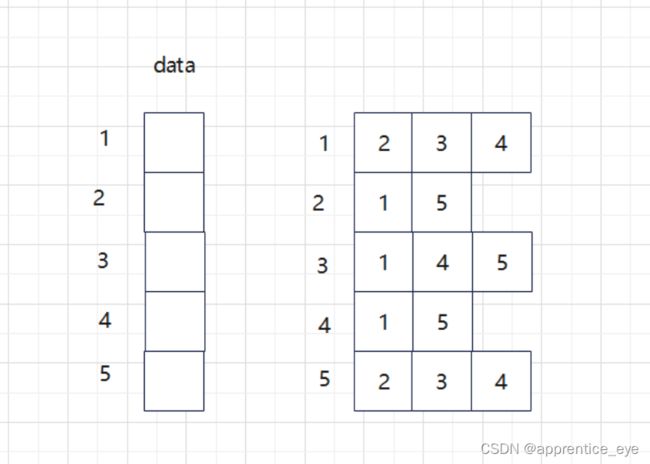
为什么要用链表呢?一个顶点连接的其他顶点的个数是不确定的，而链表的长度可以随心所欲的变化，正好适合存储这种信息。

实现图的创建

我们已经知道了图的两种表示形式邻接矩阵与邻接链表，现在我们开始进行图的创建，下面所有的程序示例以图的邻接矩阵形式进行演示。
首先我们要先知道图的结点的个数，只有知道了图的结点的个数n，我们才能创建一个n*n大小的矩阵来存储边的信息，然后我们将点与边加入到图中，这也就需要我们对结点进行编号，编号完成之后，我们就可以根据结点的编号将对应的信息存储到对应的位置，如果不给出确定的编号我们是无法创建图的，因为我们不知到这一个信息具体要放到哪一个位置。
如下

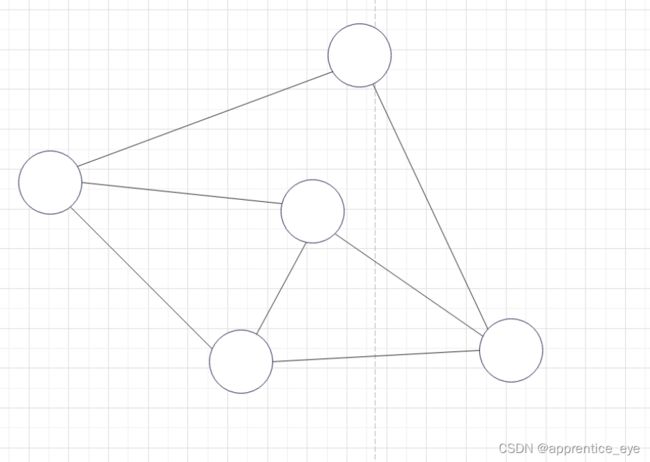
因为没有给出结点的编号，所以这一个图在创建的时候，我们需要假定一个结点作为最初的结点，然后根据邻接关系确定下一个结点，依次类推…这种行为本身就是对结点的一种编号行为。
所以第一步就是为图确定好编号，接下来就是按照编号依次将点输入，然后将边加入到邻接矩阵中去。
添加点如下图所示：

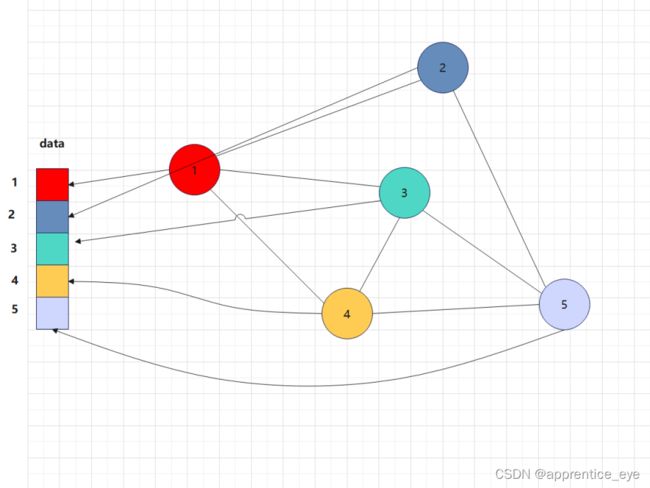
添加边时如果点i与点j之间存在边的话就将数组元素第i行第j列的元素置为1即可。
根据以上步骤就能完成图的创建。

图的遍历操作

深度优先遍历

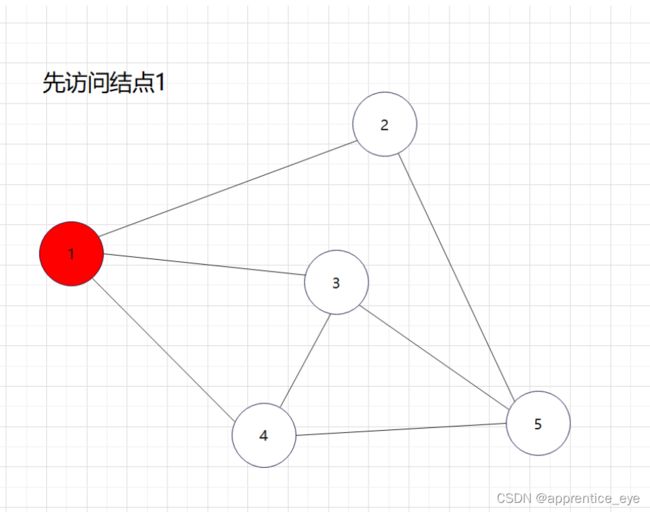
要对图完成深度优先遍历的话，就必然面临一个问题从哪一个结点作为起始顶点，因为对于图来说的话，仿佛从哪一个顶点开始进行深度优先遍历都可以，为了能够统一，接下来的深度优先遍历都是从存储数据的数组的第一个元素开始即我们编号为1的元素开始。
因为我们的图是无向图所以在我们遍历的时候可能会出现再次遇到一个已经访问过的结点，为了避免这种情况的产生，我们为每一个元素设置一个标志位，来标记结点是否被访问过，如果未被访问则访问此节点，若已访问过则不再访问此节点。
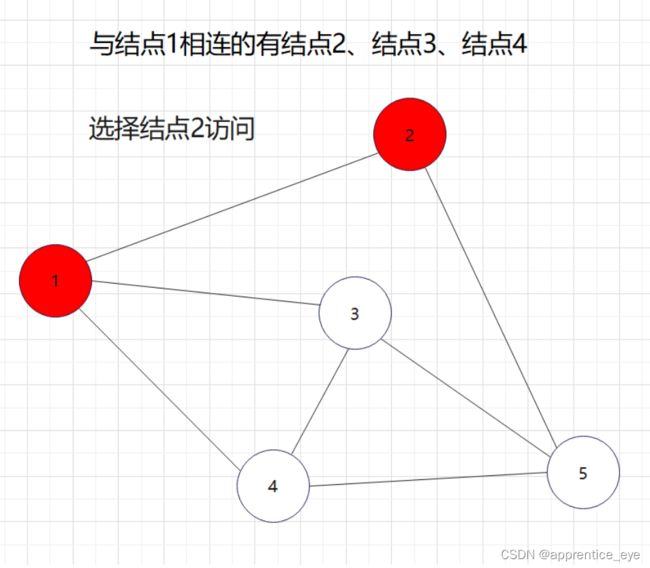
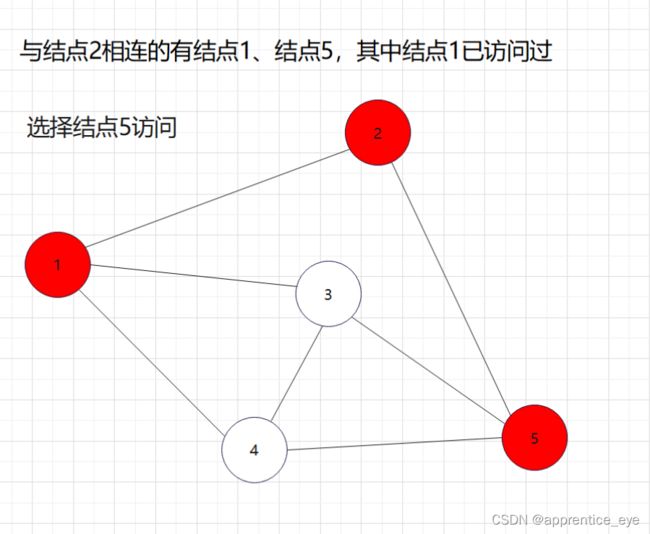
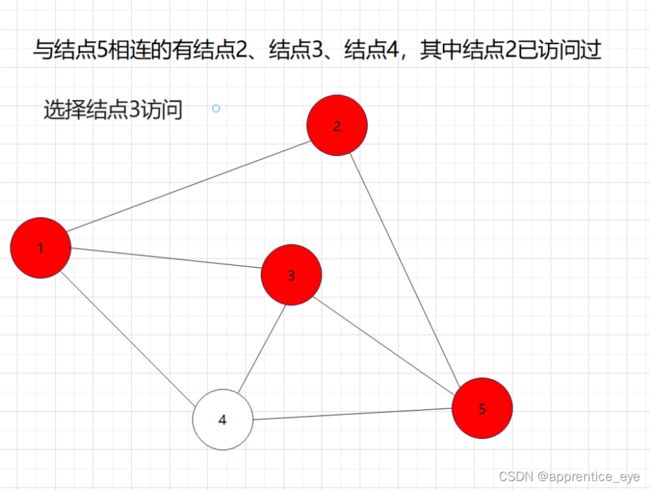
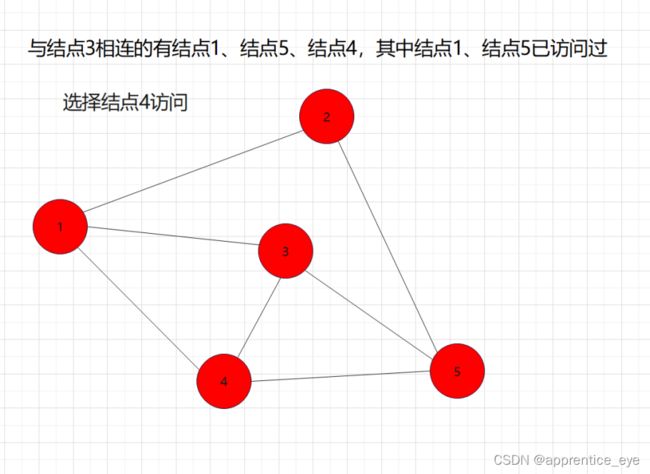
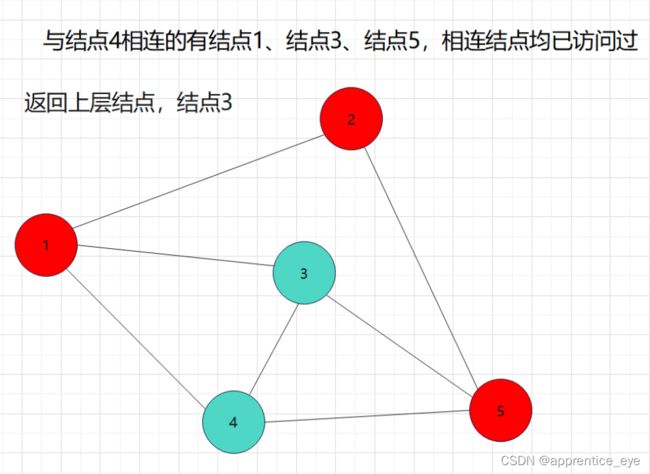
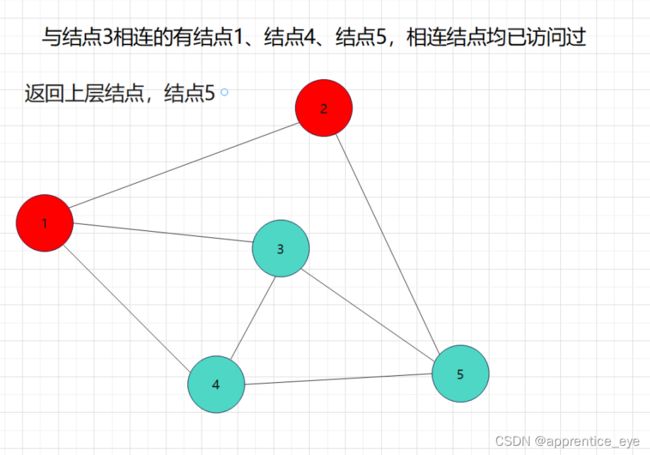
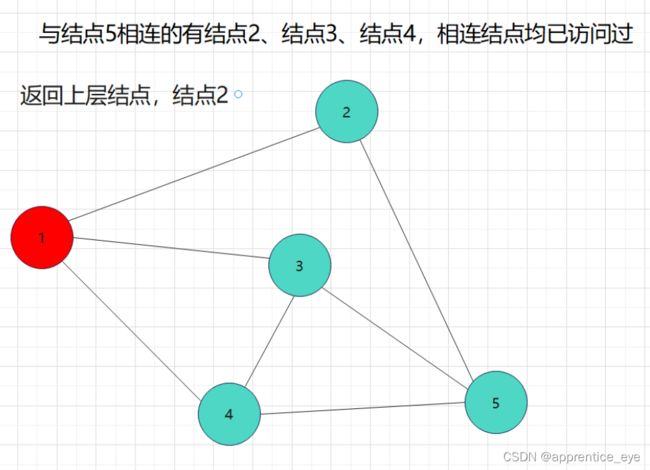
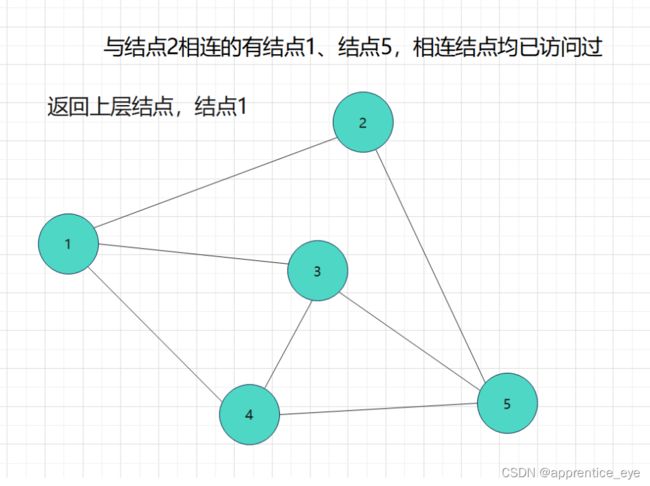
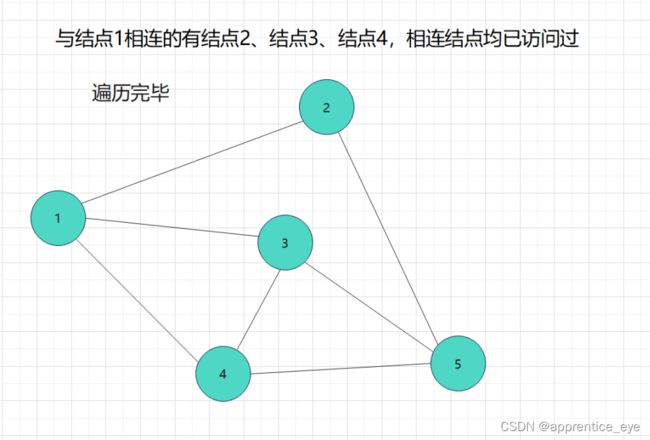
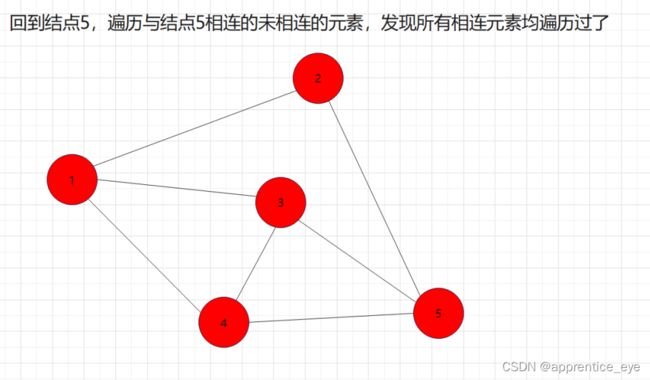
我们要的是深度优先，这也就是说如果一个结点同时与多个结点相连，我们需要选定其中一个结点访问，然后再在刚才访问过的结点相连的节点中选择一个继续访问，当无法再向更深处访问时，我们返回上一层结点，从未访问过的结点中再选择一个结点进行访问，如此进行下去直到所有元素都被访问过，则此时深度优先遍历完成。
如图所示：

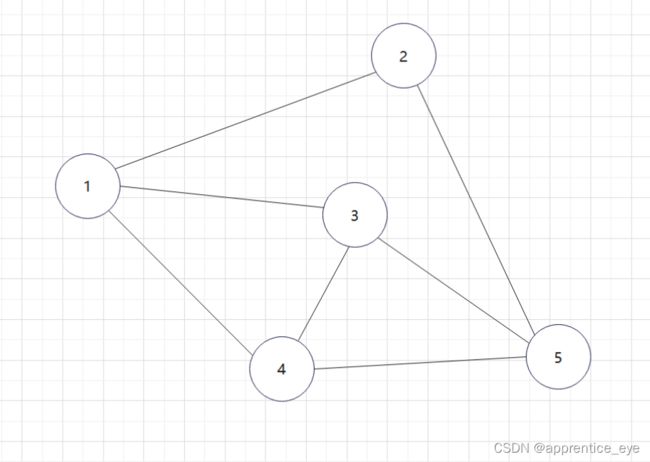
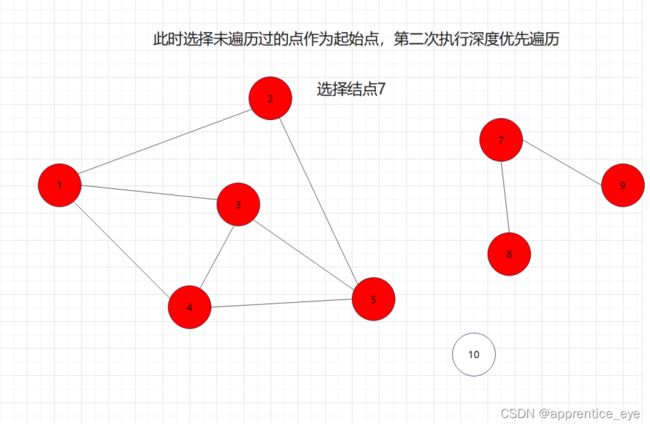
这就是一个深度优先遍历的具体过程，但是此时我们考虑的情况仅为连通图，也就是任意两个结点之间均有路径可达，但是如果像下面给出的图一样呢？

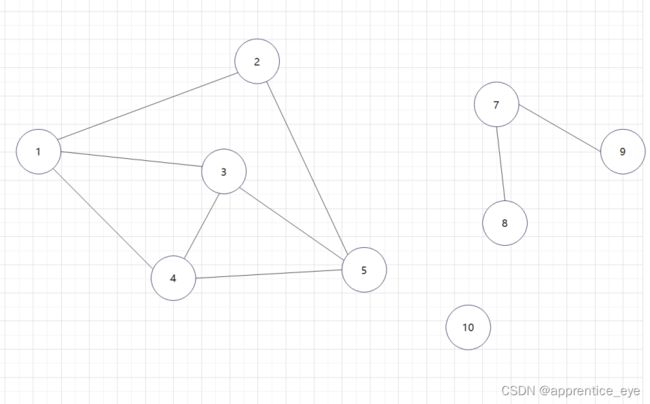
像这样给出的图，其中通过结点1进行深度优先遍历结点7、结点8、结点9与结点10是没法遍历到的，因为没有路径可达，这种我们应该怎样解决呢？
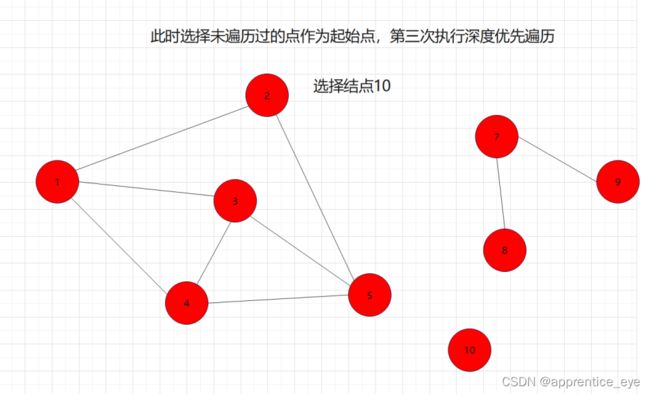
当我们选定图A中的一个结点进行深度优先遍历后，即是我们无法遍历完图A中的所有结点，但是我们遍历完了图A的一个子图B，此时我们只需要再选一个结点，此节点不在已经遍历过的结点之中，在此节点上执行依次深度优先遍历就能再遍历完图A的一个子图C，依次进行，就能将图A的所有结点遍历完。
由此我们就完成了深度优先遍历：
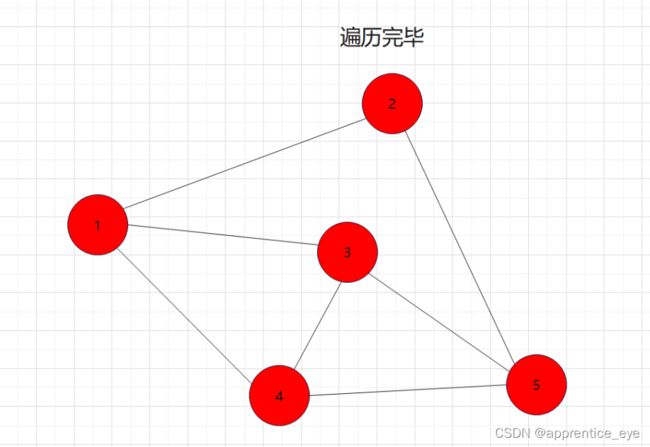
如图所示：

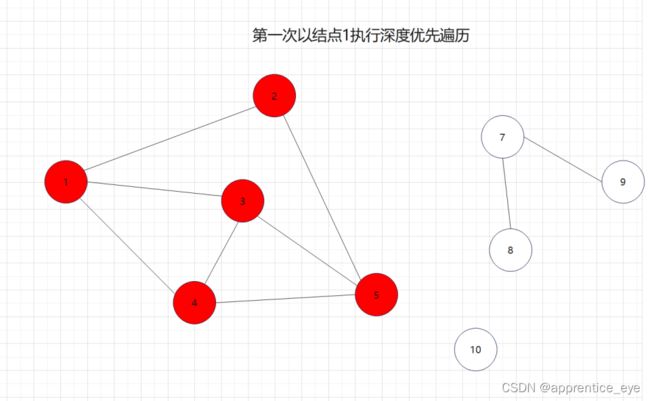
此时遍历完成。
有了上述思路我们可以写出代码如下：

void DFS(struct Graph *p, int x, char *flag){
    printf("%d ", p->data[x]);
    flag[x] = 1;
    for(int i=0; i < p->size; i++){
        if(p->arcs[x][i]!=__INT32_MAX__&&flag[i]==0){
            DFS(p, i, flag);
        }    
    }
}

广度优先遍历

对于广度优先遍历，遍历到一个结点之后优先遍历与其所有相连的结点，之后再遍历与其相连结点相连的节点，依次进行下去直到所有结点均遍历完毕。
这种遍历方式有点类似于树的层序遍历。
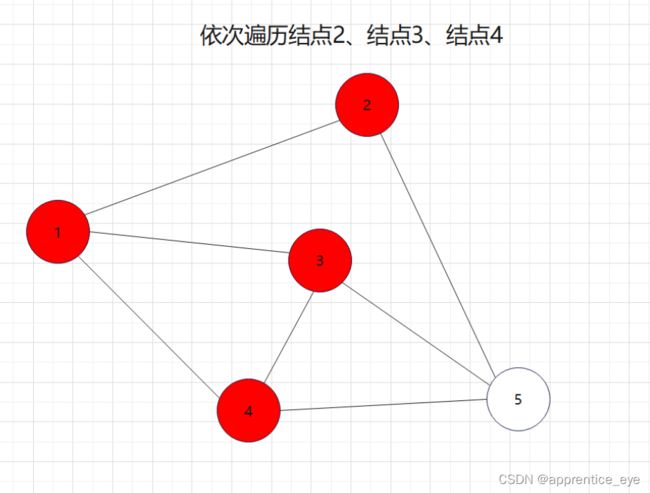
如图所示：

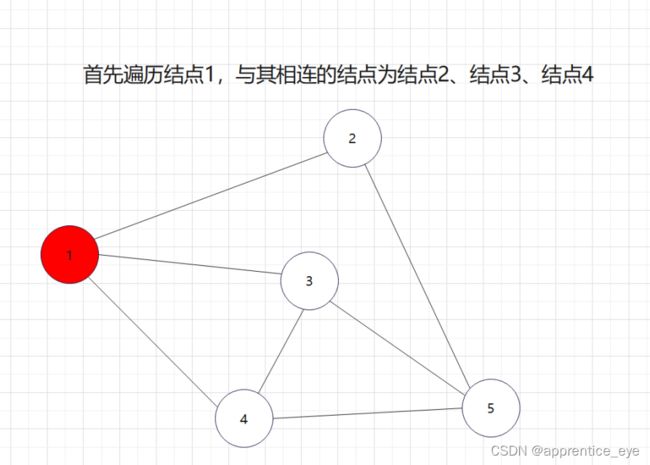
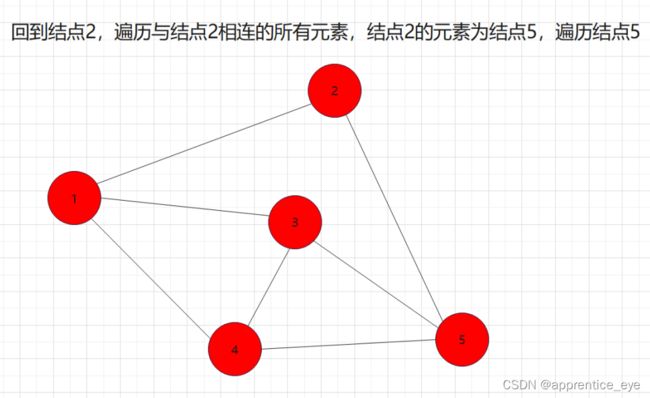
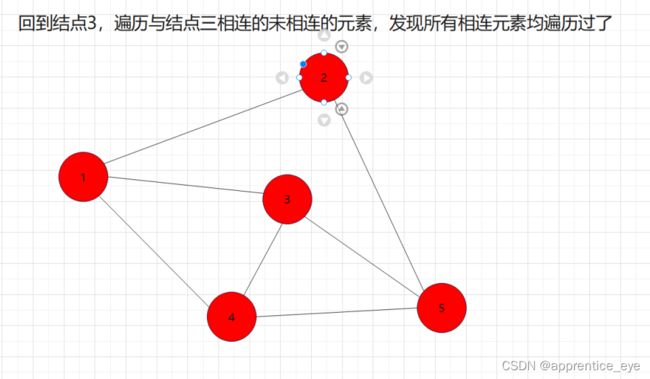
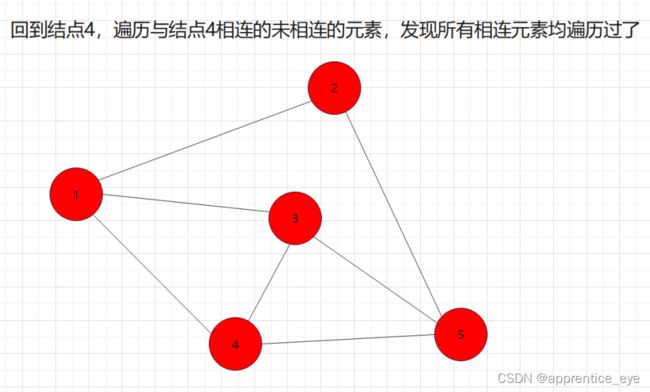
我们发现我们再遍历完结点1之后，我们接着遍历了所有与结点1相连的元素，按照顺序遍历了结点2、结点3、结点4，之后我们回到结点2，遍历与结点2相连的所有节点，然后再回到结点3，遍历与结点3相连的元素，然后再回到结点4，遍历与结点4相连的元素，然后到结点5，遍历与结点5相连的元素。遍历完毕。而在访问完结点2、结点3、结点4之后再回到结点2、结点3、结点4，如果我们不事先记录，再次访问是很困难的。所以我们要解决这一个问题。
其中我们发现，结点2、结点3、结点4依次遍历完之后，又再次按照结点2、结点3、结点4的顺序被访问了，即这些结点被访问了两次，第一次是访问结点的信息，第二次是为了通过这些结点访问与其相连的结点。而且顺序是在第一次访问过程中谁被先访问到，第二次访问仍然是谁被先访问，这是什么，这不就是先进先出吗！！所以我们在实现广度优先遍历的时候要使用队列这种数据结构进行辅助。
至此进行广度优先遍历已经被剖析完毕，代码实现如下：

void BFS(struct Graph *p, char *flag, struct Queue * q){
    for(int i=0; i < p->size; i++){
        if(flag[i]==0){
            q->rear->index = i;
            q->rear->next = (struct QueueNode *)malloc(sizeof(struct QueueNode));
            q->rear = q->rear->next;
            printf("%d ", p->data[i]);
            flag[i] = 1;
            while(q->front!=q->rear){
                struct QueueNode * t = q->front;
                q->front = q->front->next;
                int num = t->index;
                free(t);
                for(int j = 0; j < p->size; j++){
                    if(p->arcs[num][j]!=__INT32_MAX__&&flag[j]==0){
                        q->rear->index = j;
                        q->rear->next = (struct QueueNode *)malloc(sizeof(struct QueueNode));
                        q->rear = q->rear->next;
                        printf("%d ", p->data[j]);
                        flag[j] = 1;
                    }
                }
            }
        }
    }
}

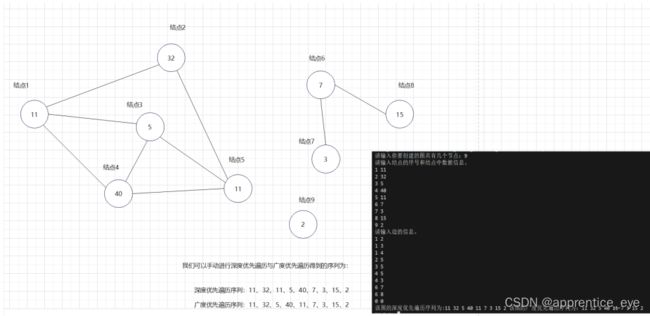
进行深度优先遍历与广度优先遍历结果验证

最小生成树

最小生成树指的是在一个有权图中可以选取其中的边使得所有的顶点之间都有一条路径可达，但是所有路径的权值相加要最小这就是最小生成树。
最小生成树的建立可以有两种算法Prim算法(加点法)和Kruskal算法(加边法)两种，首先我们来剖析一下Prim算法。

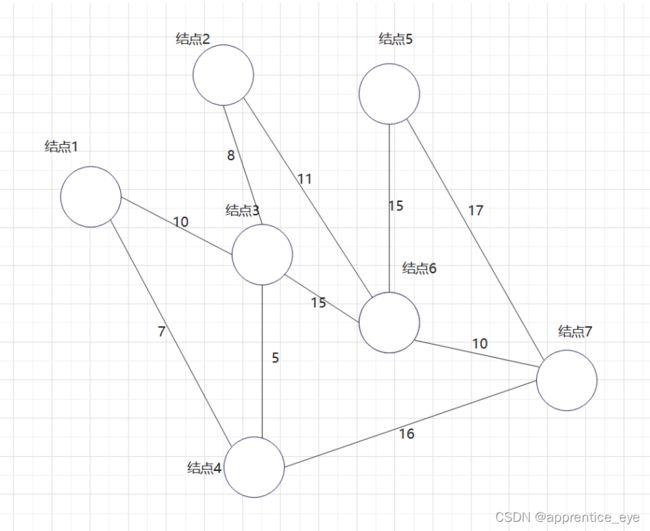
Prim算法

假设有下图所示的有权无向图：

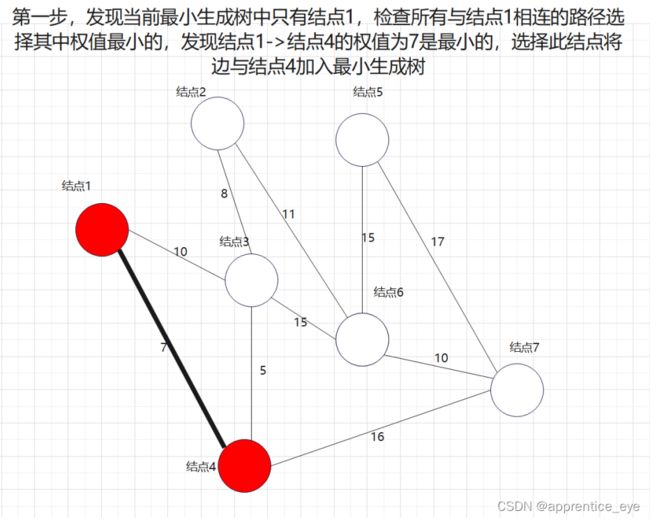
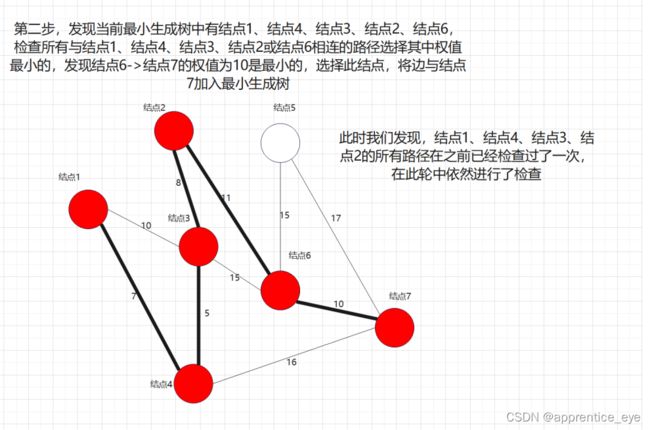
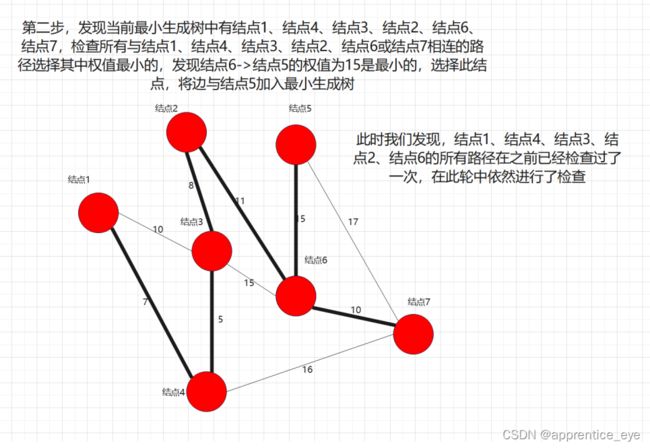
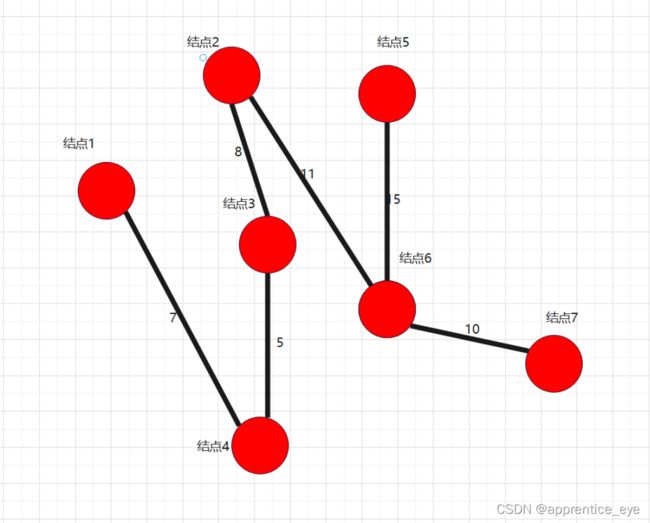
此图是一个有权无向图，我们要在建立其最小生成树，我们一定要先选择一个起始点作为操作最开始的起点，此时这一个起点所代表的就是原图的一个子图，如果我们每一次向此子图中添加的图都是离此图权值最小的路径，那么最后我们不就能得到最小生成树了吗？
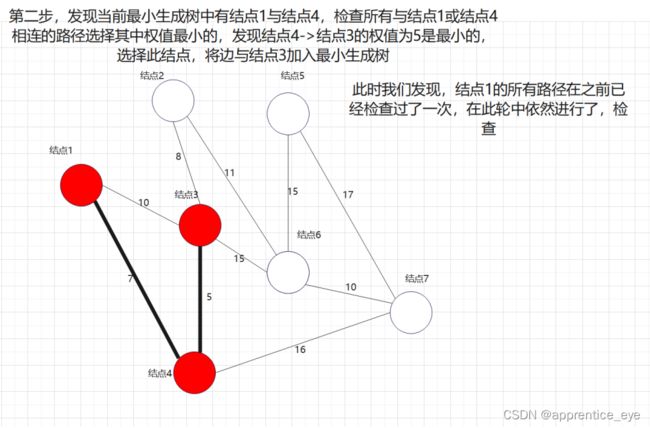
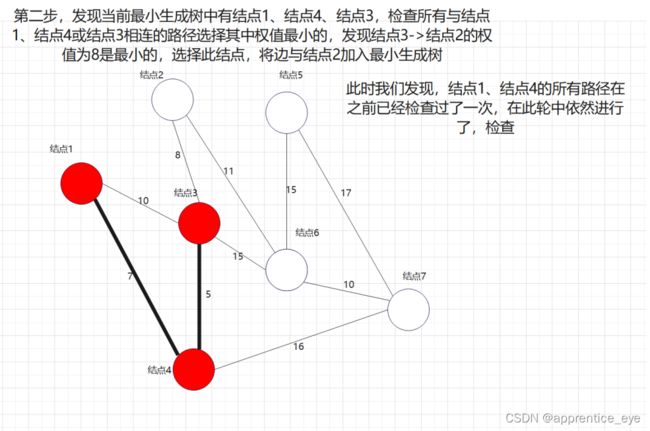
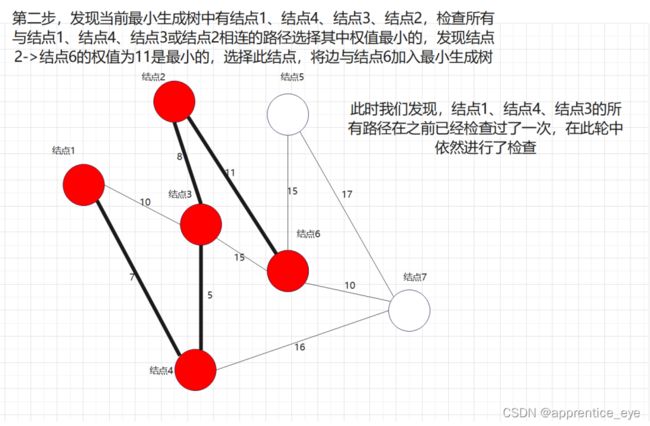
说做就做，我们在上述图中做最小生成树的操作：

最后我们建成的最小生成树就如下图所示：

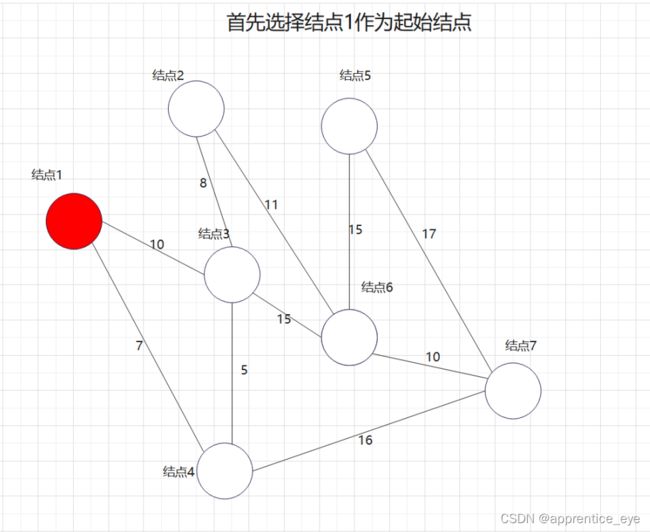
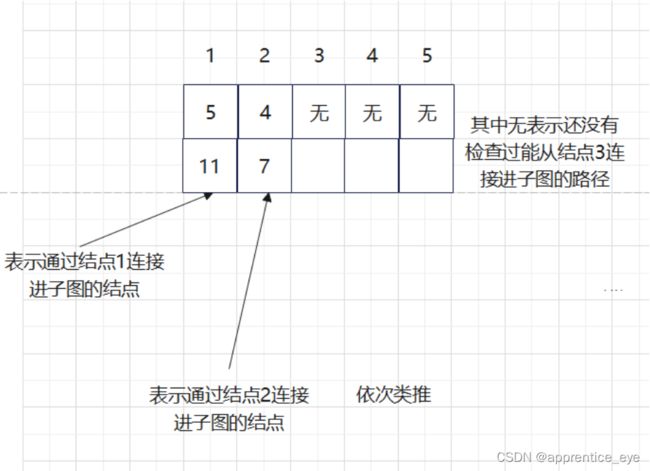
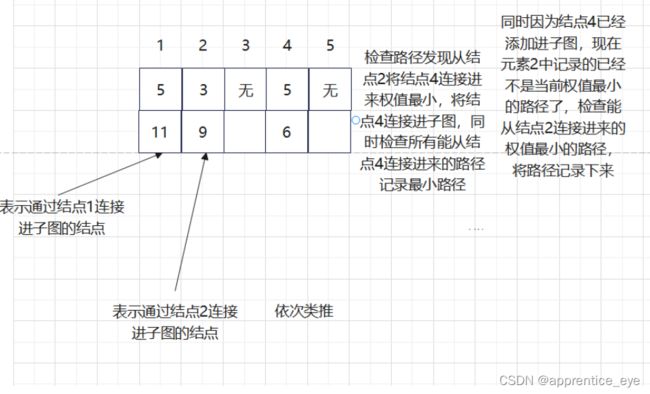
另外我们在建立最小生成树的过程中发现其中进行了大小重复的检查，这显然是对时间的极大浪费，为了能够使时间效率提高，我们需要想一个比较方便的方法能够记录能够连接到当前子图的最小路径。我们通过观察子图以及添加路径与当前子图的关系我们可以发现，所有路径都是通过在子图中的结点连接进去的，所以如果我们能够记录通过子图中已存在的结点连接进子图的最短路径作为候选路径即可，不用再每一次比较所有可能的路径。只需要在将一条通过此节点连接进子图的路径添加进子图之后更新与此连接点连接的最短路径即可，每一次候选的路径大大减少。
而且这种存储也较为方便，我们只需要用数组x其中第i个元素表示通过结点i连接进当前子图的最小路径。
存储与更新规则如下图所示：

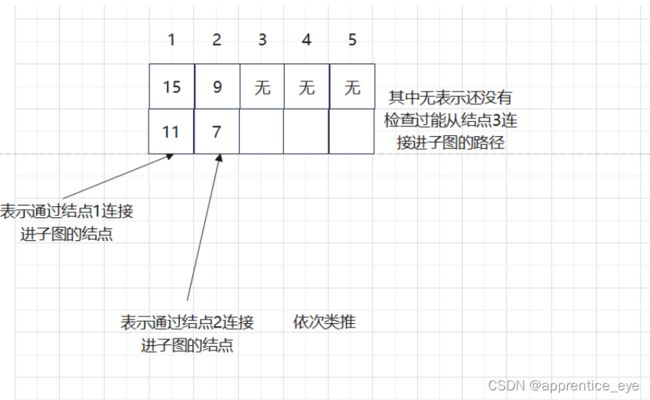
由此我们就能写出如下代码：

struct Graph * InitMST(struct Graph *p){
    struct Record *record = (struct Record *)malloc(sizeof(struct Record)*p->size);  
    for(int i = 0; i < p->size; i++){  // 初始化记录数组
        record[i].index = p->size+1;
        record[i].weight = __INT32_MAX__;
        record[i].flag = 0;
    }
    struct Graph * q = (struct Graph *)malloc(sizeof(struct Graph)); // 创建一个最小生成树的图
    q->size = 0;
    for(int i=0; i<MAX_SIZE; i++){  //将最小生成树的邻接矩阵初始化
        q->data[i] = p->data[i];
        for(int j=0; j<MAX_SIZE; j++){
            q->arcs[i][j] = __INT_MAX__;
        }
    }
    q->size += 1;
    record[0].flag = 1;
    for(int i=0; i<p->size;i++){
        if(p->arcs[0][i]<record[0].weight){
            record[0].index = i;
            record[0].weight = p->arcs[0][i];
        }
    }
    while(q->size!=p->size){
        printf("\n");
        for(int i=0; i<p->size; i++){ // 每一次添加完毕之后输出邻接矩阵
            for(int j=0; j<p->size; j++){
                if(q->arcs[i][j]==__INT32_MAX__){
                    printf(" 0 ");
                }else{
                    printf("%2d ", q->arcs[i][j]);
                }
            }
            printf("\n");
        }
        int index = 0;
        for(int i=0; i<p->size; i++){  // 从现在已有的结点向子图中添加点与边
            if(record[i].weight<record[index].weight){
                index = i;
            }
        }
        q->size += 1;// 结点数增加
        q->arcs[index][record[index].index] = record[index].weight; // 加入边
        q->arcs[record[index].index][index] = record[index].weight;
        record[record[index].index].flag = 1; //标记点是否在子图之中
        for(int j = 0; j < p->size; j++){ // 刚添加的哪一个点，同样可以有通过其连入子图的路径
            if(p->arcs[record[index].index][j]<record[record[index].index].weight&&record[j].flag==0){ 
                record[record[index].index].weight = p->arcs[record[index].index][j];
                record[record[index].index].index = j;
            }
        }
        for(int k = 0; k<p->size; k++){
            if(record[record[k].index].flag == 1){
                record[k].weight = __INT32_MAX__; // 将权重置为最大
                record[k].index = p->size+1;
                for(int j = 0; j<p->size; j++){ // 因为刚才从其引入了一个边
                    if(p->arcs[index][j]<record[index].weight&& record[j].flag==0){ // 更新存储信息,更新的那一条边不用向其中添加
                        record[index].weight = p->arcs[index][j];
                        record[index].index = j;
                    }
                }
            }
        }
    }
    printf("\n");
    for(int i=0; i<p->size; i++){
        for(int j=0; j<p->size; j++){
            if(q->arcs[i][j]==__INT32_MAX__){
                printf(" 0 ");
            }else{
                printf("%2d ", q->arcs[i][j]);
            }
        }
        printf("\n");
    }
    for(int i = 0; i<p->size; i++){
        printf("%d \n", q->data[i]);
    }
    return q;
}

运行结果：
在输出是，为了方便显示将无穷显示为0

如果有什么地方讲的不好或者讲错的地方欢迎大家指出来，如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦！

我是你们的好伙伴apprentice_eye

一个致力于让知识变的易懂的博主。