fmincon函数求解非线性超越方程的学习记录
最近的算法中用到了fmincon函数,寻找多变量非线性方程最小值的函数;因此学习一下;
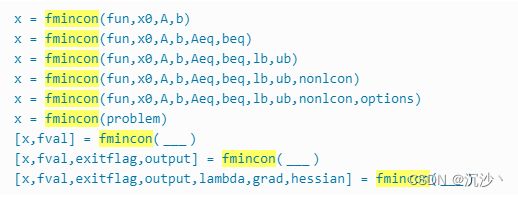
fmincon函数的基础语法如下所示:
fmincon函数是为了求解下列方程的最小值;
b 和 beq 是向量,A 和 Aeq 是矩阵,c(x) 和 ceq(x) 是返回向量的函数,f(x) 是返回标量的函数。f(x)、c(x) 和 ceq(x) 可以是非线性函数。x、lb 和 ub 可以作为向量或矩阵传递;
1 应用一:求解线性不等式约束方程
x= fmincon(fun,x0,A,b),从 x0 开始,尝试在满足线性不等式 A*xx。x0 可以是标量、向量或矩阵。
代码实例:
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
x0 = [-1,2];
A = [1,2];
b = 1;
x = fmincon(fun,x0,A,b)代码功能:
函数: f [x(1),x(2)] = 100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
从点[-1,2]开始求最小值,约束方程为: x(1)+2x(2) <= 1 。 这个方程的系数矩阵为 [1,2],最大值为1,因此设置 A = [1,2] , b = 1 ,最终函数以 A*x < b 形式表达此约束。
代码运行结果:
这个应用是较为简单的,总之就是通过fun设置函数;通过A和b的值设置约束方程;通过x0设值参数 x(1)和 x(2)的最小值;函数输出的结果x就是函数在满足约束条件达到最小值时的x(1)和 x(2)的大小;
2 应用二:线性不等式和等式共同约束的极值求解
在既有线性不等式约束又有线性等式约束的情况下求 Rosenbrock 函数的最小值。
将目标函数 fun 设置为 Rosenbrock 函数。
x = fmincon(fun,x0,A,b,Aeq,beq) : 在满足线性等式 Aeq * x = beq 以及不等式 A*xfun。如果不存在不等式,则设置 A = [] 和 b = []。
代码实例:
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
x0 = [0.5,0];
A = [1,2];
b = 1;
Aeq = [2,1];
beq = 1;
x = fmincon(fun,x0,A,b,Aeq,beq)代码功能:
函数: fun = 100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
从点 [0.5,0] 开始求最小值,约束为 x(1)+2x(2)≤1 和 2x(1)+x(2)=1。
-
以
A = [1,2]和b = 1为条件,以A*x <= b形式表达线性不等式约束。这个方程的系数矩阵为 [1,2],最大值为1,因此设置 A = [1,2] , b = 1 ,最终函数以 A*x < b 形式表达此约束。 -
以
Aeq = [2,1]和beq = 1为条件,以Aeq*x = beq形式表达线性等式约束。这个方程的系数矩阵为 [2,1],方程值 =1 ,因此设置 Aeq = [2,1] , beq = 1 ,最终函数以 Aeq*x = beq 形式表达此约束。
代码运行结果:
3 应用三:具有边界约束的极值求解
在存在边界约束的情况下,求目标函数的最小值。目标函数是具有两个变量的简单代数函数。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) :对 x 中的设计变量定义一组下界和上界,使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式,请设置 Aeq = [] 和 beq = []。如果 x(i) 无下界,请设置 lb(i) = -Inf,如果 x(i) 无上界,请设置 ub(i) = Inf。
代码实例:
fun = @(x)1+x(1)/(1+x(2)) - 3*x(1)*x(2) + x(2)*(1+x(1));
% x 为正值且满足 x(1) ≤ 1 和 x(2) ≤ 2 的区域。
lb = [0,0];
ub = [1,2];
% 无任何线性约束
A = [];
b = [];
Aeq = [];
beq = [];
%尝试使用一个位于区域中部的初始点
x0 = (lb + ub)/2;
%输出结果
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)代码功能:
函数: fun = 1+x(1)/(1+x(2)) - 3*x(1)*x(2) + x(2)*(1+x(1));
无任何约束,但是 x的值存在边界条件: x 为正值且满足 x(1) ≤ 1 和 x(2) ≤ 2 , 即 x(1)的下界为0,上界为1,x(2)的下界为0,上界为2;因此设置下界与上界的矩阵 lb = [0,0]; ub = [1,2]; 表达此边界条件,最终输出结果;
值得注意的是初始点的选取;目前是尝试使用一个位于区域中部的初始点,即x0 = (lb + ub)/2;这个值不同将会影响系统的输出结果,因为求解函数的单个方向收敛的,这个初值的设置需要参考不同函数进行独立的设计。
代码运行结果:
3 应用四:具有非线性约束的极值求解
在非线性约束下求函数的最小值,这个非线性约束是指那些 既不是边界、也不是线性等式、也不是不等式的情况,比如某个函数在某个区域内的极小值,这个区域是一个圆或者是一个正方型区域,这个限制条件就是非线性的约束条件;
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) : 求解非线性约束 nonlcon 函数下函数极值;满足 nonlcon 所定义的非线性不等式 c(x) 或等式 ceq(x)。fmincon 进行优化,以满足 c(x) ≤ 0 和 ceq(x) = 0。如果不存在边界,请设置 lb = [] 和/或 ub = []。
代码实例:在边界约束下求 Rosenbrock 函数在圆内最小的点,理想输出结果是x1 = 0.5,x2 = 0.25
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
% x1 = [0 0.5] , x2 = [0.2 0.8] 区域内寻找
lb = [0,0.2];
ub = [0.5,0.8];
%没有线性约束,因此将这些参数设置为 []。
A = [];
b = [];
Aeq = [];
beq = [];
%选择一个满足所有约束的初始点。
x0 = [1/4,1/4];
%求解输出(尾部定义非线性约束)
nonlcon = @circlecon;
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
%同时在以 [1/3,1/3] 为圆心、半径为 1/3 的圆内寻找。将以下代码复制到您的 MATLAB® 路径上名为 circlecon.m 的文件中。
function [c,ceq] = circlecon(x)
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
ceq = [];
end
代码功能:在边界约束下求 Rosenbrock 函数在圆内最小的点
无任何线性约束,仅存在一个约束条件:极值必须在以 [1/3,1/3] 为圆心、半径为 1/3 的圆内寻找。
非常值得注意的是这个 nonlcon函数的撰写;
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2; 这是所需圆的表达式;由于该函数规定必须是满足 c(x) ≤ 0 。因此要表示在圆内, 将原本圆的表达式是 : (x(1)-1/3)^2 + (x(2)-1/3)^2 =(1/3)^2,转换为c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
假如需要增加参数之间的关系: 增加类似 c = x(1) - x(2),表示 x(2)>= x(1)
ceq = [],此时不存在等式,这里选择为空即可;
这些都是单个约束条件 ,如果有多个约束条件就是 c(1) = ..... c(2) = ....即可
代码运行结果: