2023/12/24周报
文章目录
- 摘要
- Abstract
- 文献阅读
-
- 1.题目
- 2.创新点
- 3.方法
-
- 3.1 降水临近预报问题的表述
- 3.2 序列建模的长短期记忆
- 4.模型
-
- 4.1 卷积LSTM
- 4.2 将2D图像转换为3D张量
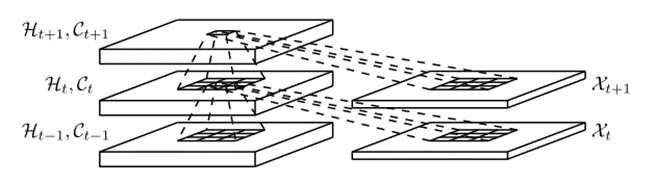
- 4.3 Encoding-forecasting
- 5.实验
-
- 5.1 实验过程
- 5.2 实验结果
- 深度学习
-
- ConvLSTM概念
- 基于pytorch实现ConvLSTM
- 总结
摘要
本周阅读了一篇关于降水序列预测的论文,文中制定了降水临近预报的时空序列预测问题,其中输入和预测目标都是时空序列,通过扩展完全连接的LSTM(FC-LSTM),使其在输入到状态和状态到状态的转换中都具有卷积结构,提出了卷积LSTM。最后对卷积LSTM理论进行学习,并使用代码实现卷积LSTM。
Abstract
This week, a paper on the prediction of precipitation series is readed. In this paper, the problem of time-space series prediction of precipitation approaching prediction is formulated, in which the input and prediction targets are both time-space series. By extending the fully connected LSTM(FC-LSTM), it has a convolution structure in the transformation from input to state and state to state, and a convolution LSTM is proposed. Finally, the theory of convolution LSTM is studied, and the convolution LSTM is realized by code.
文献阅读
1.题目
Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting
2.创新点
降水临近预报的目的是预测局部地区未来较短时间内的降水强度。以前很少有研究从机器学习的角度来研究这个关键而具有挑战性的天气预报问题。在本文中制定了降水临近预报的时空序列预测问题,其中输入和预测目标都是时空序列。通过扩展完全连接的LSTM(FC-LSTM),使其在输入到状态和状态到状态的转换中都具有卷积结构,提出了卷积LSTM(ConvLSTM),并使用它来构建降水临近预报问题的端到端可训练模型。实验表明,文章提出的ConvLSTM网络能够更好地捕捉时空相关性,并且在降水临近预报方面始终优于FC-LSTM和最先进的操作ROVER算法。
3.方法
3.1 降水临近预报问题的表述
假设在一个由M行N列组成的M×N网格表示的空间区域上观察一个动力系统。在网格中的每个单元格内,有随时间变化的P测量值。因此,任何时刻的观测都可以表示为张量X ∈ RP×M×N,其中R表示观测特征的域。如果周期性地记录观测,将得到一个张量序列X1,X2,…,Xt.时空序列预测问题是在给定包括当前观测值的先前J个观测值的情况下预测未来最可能的长度为K的序列:
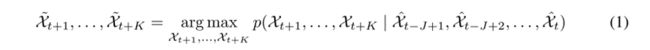
3.2 序列建模的长短期记忆
LSTM作为一种特殊的RNN结构,在以前的各种研究中已经证明了它的稳定性和强大性,可以对长距离依赖关系进行建模:
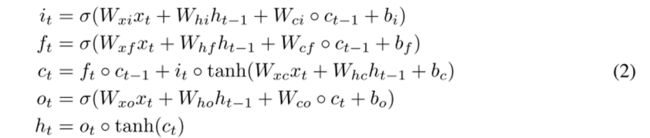
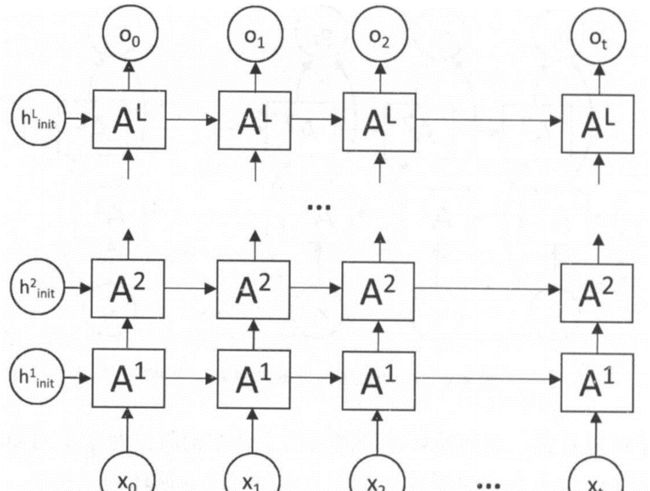
多个LSTM可以堆叠并在时间上连接以形成更复杂的结构。这种模型已被应用于解决许多现实生活中的序列建模问题。
4.模型
FC-LSTM在处理时空数据方面的主要缺点是它在没有进行空间信息编码的输入到状态和状态到状态的转换中使用了完全连接,缺乏空间信息的提取;所以,文章设计了ConvLSTM:
4.1 卷积LSTM
三个输入,记忆单元、隐藏状态和输入X都由一维变为三维张量。使用Zero-padding来进行填充C和H,达到和X的行数和列数是一样的。作者也解释了Zero-padding的好处。
ConvLSTM的关键方程如下面的(3)所示:

*表示卷积,⭕是hadamard积。公式其实就是把input-to-state, state-to-state 的正常乘积运算,用术语叫做hadamard乘积,改为卷积运算。本质上没有变化,做的事情基本上是将向量与权重的乘积,换成了卷积,这样能大大减少参数量。
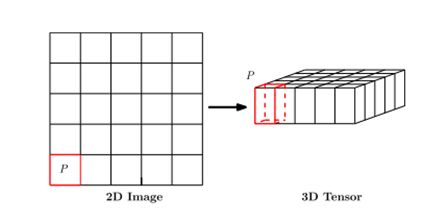
4.2 将2D图像转换为3D张量
降水临近预报的目标是利用先前观测到的雷达回波序列来预测当地地区(如香港、纽约或东京)的未来雷达地图的固定长度。在实际应用中,雷达地图通常每6-10分钟从天气雷达上获取一次,并在接下来的1-6小时内进行临近预报,即预测前方的6-60帧。降水预报实际上是时空预测问题。
每个正方形小格点代表11公里可以看做一个地区。p值为降雨量,也可以为雷达反射率,它和降雨量之间有关系可以转换。对于雷达回波图来说每一个图片的对应像素点通过一定的变换其实是可以直接得到这个点的一些物理量的,所以这个P实际作者想说的就是这个物理量的维度。
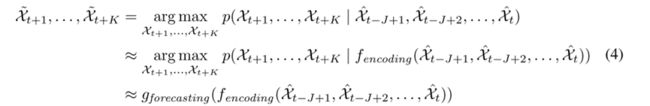
4.3 Encoding-forecasting
两个网络、一个编码网络和一个预测网络。类似于中,预测网络的初始状态和单元输出是从编码网络的最后一个状态复制出来的。这两个网络都是通过堆叠几个ConvLSTM层来形成的。由于我们的预测目标具有与输入相同的维数,所以我们将预测网络中的所有状态连接起来,并将它们送入 1 × 1 卷积层,以生成最终预测。
5.实验
5.1 实验过程
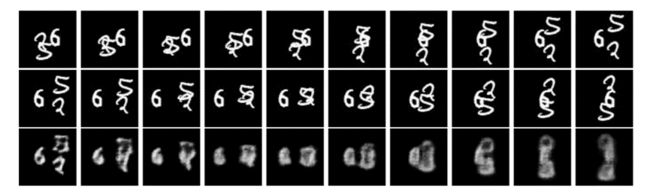
使用Moving-MNIST数据集:数据集为图中有两个数字的时空序列的移动。 大小为64乘以64, 整个序列为20,前十个为输入数据,后十个为预测数据。移动数字是从MNIST数据集中的500位数字的子集中随机选择的。起始位置和速度方向均匀随机选择,速度振幅随机选择。这个生成过程重复15000次,得到一个包含10000个训练序列、2000个验证序列和3000个测试序列的数据集。
所有的模型的均采用cross-entropy交叉熵作为损失函数,用的optimizer为RMSProp, 学习率为0.001并且有0.9的延迟率。对比FC-LSTM以及不同架构ConvLSTM参数多少以及交叉熵的结果。
5.2 实验结果
对于ConvLSTM网络,本文将补丁大小设置为4×4,以便每个64×64帧用一个16×16×16张量表示。
ConvLSTM的三种变体:
1层网络包含一个有256个隐藏状态的ConvLSTM层,
2层网络有两个ConvLSTM层,每层有128个隐藏状态,
3层网络在三个ConvLSTM层中分别有128、64和64个隐藏状态。

-5x5 ‘和’ -1x1 ‘表示相应的状态对状态内核大小,即5×5或1×1。“256”、“128”和“64”表示ConvLSTM层中隐藏状态的数量。’ (5x5) ‘和’ (9x9) '表示输入到状态的内核大小;
每个模型不管是多少层的,input-to-state的kernel size都为一致的,只有每层的state-to-state的kernel size在变,以及 hidden state的大小在变。
深度学习
ConvLSTM概念
用于降水预测,核心思想是卷积替代hadamard乘积。
普通的LSTM如下:
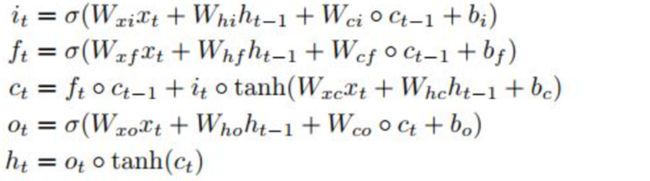
其中的 o 表示hadamard乘积,其实就是矩阵相乘,相当于全连接神经网络(一层全连接网络就是相当于一个矩阵相乘),全连接网络参数量巨大,不能有效提取空间信息,把它换为卷积之后则能有效提取空间信息(花书中使用卷积层替代全连接层的动机),于是把hadamard乘积改为卷积。
于是就有了ConvLSTM:
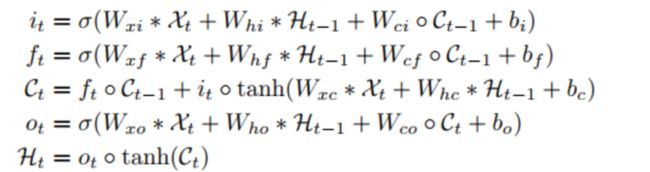
ConvLSTM的结构图如下:
区别也就是一个输入的是一维序列,另一个是二维图片;处理一维序列使用的是卷积全连接神经网络,处理二维图片使用的是卷积神经网络。

基于pytorch实现ConvLSTM
import numpy as np
from torch.utils.data import Dataset,DataLoader
import torch
import torch.nn as nn
"""
定义ConvLSTM每一层的、每个时间点的模型单元,及其计算。
"""
class ConvLSTMCell(nn.Module):
def __init__(self, input_dim, hidden_dim, kernel_size, bias):
"""
单元输入参数如下:
input_dim: 输入张量对应的通道数,对于彩图为3,灰图为1。
hidden_dim: 隐藏状态的神经单元个数,也就是隐藏层的节点数,应该可以按计算需要“随意”设置。
kernel_size: (int, int),卷积核,并且卷积核通常都需要为奇数。
bias: bool,单元计算时,是否加偏置,通常都要加,也就是True。
"""
super(ConvLSTMCell, self).__init__() #self:实例化对象,__init__()定义时该函数就自动运行,
#super()是实例self把ConvLSTMCell的父类nn.Modele的__init__()里的东西传到自己的__init__()里
#总之,这句是搭建神经网络结构必不可少的。
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.kernel_size = kernel_size
self.padding = kernel_size[0] // 2, kernel_size[1] // 2 #//表示除法后取整数,为使池化后图片依然对称,故这样操作。
self.bias = bias
"""
nn.Conv2D(in_channels,out_channels,kernel_size,stride,padding,dilation=1,groups=1,bias)
二维的卷积神经网络
"""
self.conv = nn.Conv2d(in_channels=self.input_dim + self.hidden_dim, #每个单元的输入为上个单元的h和这个单元的x,
#所以h和x要连接在一起,在x的通道数上与h的维度上相连。
out_channels=4 * self.hidden_dim, #输入门,遗忘门,输出门,激活门是LSTM的体现,
#每个门的维度和隐藏层维度一样,这样才便于进行+和*的操作
#输出了四个门,连接在一起,后面会想办法把门的输出单独分开,只要想要的。
kernel_size=self.kernel_size,
padding=self.padding,
bias=self.bias)
def forward(self, input_tensor, cur_state):
"""
input_tensor:此时还是四维张量,还未考虑len_seq,[batch_size,channels,h,w],[b,c,h,w]。
cur_state:每个时间点单元内,包含两个状态张量:h和c。
"""
h_cur, c_cur = cur_state #h_cur的size为[batch_size,hidden_dim,height,width],c_cur的size相同,也就是h和c的size与input_tensor相同
combined = torch.cat([input_tensor, h_cur], dim=1) #把input_tensor与状态张量h,沿input_tensor通道维度(h的节点个数),串联。
#combined:[batch_size,input_dim+hidden_dim,height,weight]
combined_conv = self.conv(combined) #Conv2d的输入,[batch_size,channels,height,width]
#Conv2d的输出,[batch_size,output_dim,height,width],这里output_dim=input_dim+hidden_dim
cc_i, cc_f, cc_o, cc_g = torch.split(combined_conv, self.hidden_dim, dim=1) #将conv的输出combined_conv([batch_size,output_dim,height,width])
#分成output_dim这个维度去分块,每个块包含hidden_dim个节点信息
#四个块分别对于i,f,o,g四道门,每道门的size为[b,hidden_dim,h,w]
i = torch.sigmoid(cc_i) # 输入门
f = torch.sigmoid(cc_f) # 遗忘门
o = torch.sigmoid(cc_o) # 输出门
g = torch.tanh(cc_g) #激活门
c_next = f * c_cur + i * g #主线,遗忘门选择遗忘的+被激活一次的输入,更新长期记忆。
h_next = o * torch.tanh(c_next) #短期记忆,通过主线的激活和输出门后,更新短期记忆(即每个单元的输出)。
return h_next, c_next #输出当前时间点输出给下一个单元的,两个状态张量。
def init_hidden(self, batch_size, image_size):
"""
初始状态张量的定义,也就是说定义还未开始时输入给单元的h和c。
"""
height, width = image_size
init_h = torch.zeros(batch_size, self.hidden_dim, height, width, device=self.conv.weight.device) #初始输入0张量
init_c = torch.zeros(batch_size, self.hidden_dim, height, width, device=self.conv.weight.device) #[b,hidden_dim,h,w]
#self.conv.weight.device表示创建tensor存放的设备
#和conv2d进行的设备相同
return (init_h,init_c)
"""
定义整个ConvLSTM按序列和按层数的结构和计算。
输入介绍:
五维数据,[batch_size,len_seq,channels,height,width] or [l,b,c,h,w]。
输出介绍:
输出两个列表:layer_output_list和last_state_list。
列表0:layer_output_list--单层列表,每个元素表示一层LSTM层的输出h状态,每个元素的size=[b,l,hidden_dim,h,w]。
列表1:last_state_list--双层列表,每个元素是一个二元列表[h,c],表示每一层的最后一个时间单元的输出状态[h,c],
h.size=c.size=[b,hidden_dim,h,w]
使用示例:
>> x = torch.rand((64, 20, 1, 64, 64))
>> convlstm = ConvLSTM(1, 30, (3,3), 1, True, True, False)
>> _,last_states = convlstm(x)
>> h = last_states[0][0] #第一个0表示要第1层的列表,第二个0表示要h的张量。
"""
class ConvLSTM(nn.Module):
"""
输入参数如下:
input_dim:输入张量对应的通道数,对于彩图为3,灰图为1。
hidden_dim:h,c两个状态张量的节点数,当多层的时候,可以是一个列表,表示每一层中状态张量的节点数。
kernel_size:卷积核的尺寸,默认所有层的卷积核尺寸都是一样的,也可以设定不同的lstm层的卷积核尺寸不同。
num_layers:lstm的层数,需要与len(hidden_dim)相等。
batch_first:dimension 0位置是否是batch,是则True。
bias:是否加偏置,通常都要加,也就是True。
return_all_layers:是否返回所有lstm层的h状态。
"""
def __init__(self, input_dim, hidden_dim, kernel_size, num_layers,
batch_first=True, bias=True, return_all_layers=False):
super(ConvLSTM, self).__init__()
self._check_kernel_size_consistency(kernel_size) #后面def了的,检查卷积核是不是列表或元组。
kernel_size = self._extend_for_multilayer(kernel_size, num_layers) # 如果为多层,将卷积核以列表的形式分入多层,每层卷积核相同。
hidden_dim = self._extend_for_multilayer(hidden_dim, num_layers) # 如果为多层,将隐藏节点数以列表的形式分入多层,每层卷积核相同。
if not len(kernel_size) == len(hidden_dim) == num_layers: # 判断卷积层数和LSTM层数的一致性,若不同,则报错。
raise ValueError('Inconsistent list length.')
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.kernel_size = kernel_size
self.num_layers = num_layers
self.batch_first = batch_first
self.bias = bias
self.return_all_layers = return_all_layers #一般都为False。
cell_list = [] #每个ConvLSTMCell会存入该列表中。
for i in range(0, self.num_layers): # 当LSTM为多层,每一层的单元输入。
if i==0:
cur_input_dim = self.input_dim #一层的时候,单元输入就为input_dim,多层的时候,单元第一层输入为input_dim。
else:
cur_input_dim = self.hidden_dim[i - 1] #多层的时候,单元输入为对应的,前一层的隐藏层节点情况。
cell_list.append(ConvLSTMCell(input_dim=cur_input_dim,
hidden_dim=self.hidden_dim[i],
kernel_size=self.kernel_size[i],
bias=self.bias))
self.cell_list = nn.ModuleList(cell_list) # 把定义的多个LSTM层串联成网络模型,ModuleList中模型可以自动更新参数。
def forward(self, input_tensor, hidden_state=None):
"""
input_tensor: 5D张量,[l, b, c, h, w] 或者 [b, l, c, h, w]
hidden_state: 第一次输入为None,
Returns:last_state_list, layer_output
"""
if not self.batch_first:
input_tensor = input_tensor.permute(1, 0, 2, 3, 4) # (t, b, c, h, w) -> (b, t, c, h, w)
if hidden_state is not None:
raise NotImplementedError()
else:
b, _, _, h, w = input_tensor.size() # 自动获取 b,h,w信息。
hidden_state = self._init_hidden(batch_size=b,image_size=(h, w))
layer_output_list = []
last_state_list = []
seq_len = input_tensor.size(1) #根据输入张量获取lstm的长度。
cur_layer_input = input_tensor #主线记忆的第一次输入为input_tensor。
for layer_idx in range(self.num_layers): #逐层计算。
h, c = hidden_state[layer_idx] #获取每一层的短期和主线记忆。
output_inner = []
for t in range(seq_len): #序列里逐个计算,然后更新。
h, c = self.cell_list[layer_idx](input_tensor=cur_layer_input[:, t, :, :, :],cur_state=[h, c])
output_inner.append(h) #第layer_idx层的第t个stamp的输出状态。
layer_output = torch.stack(output_inner, dim=1) #将第layer_idx层的所有stamp的输出状态串联起来。
cur_layer_input = layer_output #准备第layer_idx+1层的输入张量,其实就是上一层的所有stamp的输出状态。
layer_output_list.append(layer_output) #当前层(第layer_idx层)的所有timestamp的h状态的串联后,分层存入列表中。
last_state_list.append([h, c]) #当前层(第layer_idx层)的最后一个stamp的输出状态的[h,c],存入列表中。
if not self.return_all_layers: #当不返回所有层时
layer_output_list = layer_output_list[-1:] #只取最后一层的所有timestamp的h状态。
last_state_list = last_state_list[-1:] #只取最后一层的最后的stamp的输出状态[h,c]。
return layer_output_list, last_state_list
def _init_hidden(self, batch_size, image_size):
"""
所有lstm层的第一个时间点单元的输入状态。
"""
init_states = []
for i in range(self.num_layers):
init_states.append(self.cell_list[i].init_hidden(batch_size, image_size)) #每层初始单元,输入h和c,存为1个列表。
return init_states
@staticmethod #静态方法,不需要访问任何实例和属性,纯粹地通过传入参数并返回数据的功能性方法。
def _check_kernel_size_consistency(kernel_size):
"""
检测输入的kernel_size是否符合要求,要求kernel_size的格式是list或tuple
"""
if not (isinstance(kernel_size, tuple) or
(isinstance(kernel_size, list) and all([isinstance(elem, tuple) for elem in kernel_size]))):
raise ValueError('`kernel_size` must be tuple or list of tuples')
@staticmethod
def _extend_for_multilayer(param, num_layers):
"""
扩展到LSTM多层的情况
"""
if not isinstance(param, list):
param = [param] * num_layers
return param
x = torch.rand((64, 20, 1, 64, 64))
convlstm = ConvLSTM(1, 30, (3,3), 1, True, True, False)
_, last_states = convlstm(x)
h = last_states[0][0] # 第一个0表示要第一层的列表,第二个0表示要列表里第一个位置的h输出。
设定ConvLSTM为1层,每层隐藏单元节点数为30,卷积核(3,3),这个程序运行后可以发现,输入x的size为[64,20,1,64,64],输出的第一层h的size为[64,30,64,64],符合预期。
总结
本周对时序模型ConvLSTM进行学习,这是对普通LSTM进行改进,用来预测降水的模型。该模型能够更好地捕捉时空相关性,并且在降水临近预报方面始终优于FC-LSTM和最先进的操作ROVER算法。