Atcoder Beginner Contest 333 (A - F 题)
目录
- [A - Three Threes](https://atcoder.jp/contests/abc333/tasks/abc333_a)
-
- Problem Statement
-
- Constraints
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Solution
- Code
- [B - Pentagon](https://atcoder.jp/contests/abc333/tasks/abc333_b)
-
- Problem Statement
-
- Constraints
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Sample Input 3
- Sample Output 3
- Solution
- Code
- [C - Repunit Trio](https://atcoder.jp/contests/abc333/tasks/abc333_c)
-
- Problem Statement
-
- Constraints
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Sample Input 3
- Sample Output 3
- Solution
- Code
- [D - Erase Leaves](https://atcoder.jp/contests/abc333/tasks/abc333_d)
-
- Problem Statement
-
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Sample Input 3
- Sample Output 3
- Solution
- Code
- [E - Takahashi Quest](https://atcoder.jp/contests/abc333/tasks/abc333_e)
-
- Problem Statement
-
- Constraints
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Sample Input 3
- Sample Output 3
- Solution
- Code
- [F - Bomb Game 2](https://atcoder.jp/contests/abc332/tasks/abc332_f)
-
- Problem Statement
-
- Input
- Output
- Sample Input 1
- Sample Output 1
- Sample Input 2
- Sample Output 2
- Solution
- Code
- 视频题解
A - Three Threes
Problem Statement
You are given an integer N N N between 1 1 1 and 9 9 9, inclusive, as input.
Concatenate N N N copies of the digit N N N and print the resulting string.
Constraints
N N N is an integer between 1 1 1 and 9 9 9, inclusive.
Input
The input is given from Standard Input in the following format:
N N N
Output
Print the answer.
Sample Input 1
3
Sample Output 1
333
Concatenate three copies of the digit 3 3 3 to yield the string 333.
Sample Input 2
9
Sample Output 2
999999999
Solution
具体见文后视频。
Code
#include B - Pentagon
Problem Statement
A regular pentagon P P P is shown in the figure below.

Determine whether the length of the line segment connecting points S 1 S_1 S1 and S 2 S_2 S2 of P P P equals the length of the line segment connecting points T 1 T_1 T1 and T 2 T_2 T2.
Constraints
Each of S 1 S_1 S1, S 2 S_2 S2, T 1 T_1 T1, and T 2 T_2 T2 is one of the characters A, B, C, D, and E.
S 1 ≠ S 2 S_1 \neq S_2 S1=S2
T 1 ≠ T 2 T_1 \neq T_2 T1=T2
Input
The input is given from Standard Input in the following format:
S 1 S 2 S_1S_2 S1S2
T 1 T 2 T_1T_2 T1T2
Output
If the length of the line segment connecting points S 1 S_1 S1 and S 2 S_2 S2 of P P P equals the length of the line segment connecting points T 1 T_1 T1 and T 2 T_2 T2, print Yes; otherwise, print No.
Sample Input 1
AC
EC
Sample Output 1
Yes
The length of the line segment connecting point A and point C of P P P equals the length of the line segment connecting point E and point C.
Sample Input 2
DA
EA
Sample Output 2
No
The length of the line segment connecting point D and point A of P P P does not equal the length of the line segment connecting point E and point A.
Sample Input 3
BD
BD
Sample Output 3
Yes
Solution
具体见文后视频。
Code
#include C - Repunit Trio
Problem Statement
A repunit is an integer whose digits are all 1 1 1 in decimal representation. The repunits in ascending order are 1 , 11 , 111 , … 1, 11, 111, \ldots 1,11,111,….
Find the N N N-th smallest integer that can be expressed as the sum of exactly three repunits.
Constraints
N N N is an integer between 1 1 1 and 333 333 333, inclusive.
Input
The input is given from Standard Input in the following format:
N N N
Output
Print the answer.
Sample Input 1
5
Sample Output 1
113
The integers that can be expressed as the sum of exactly three repunits are 3 , 13 , 23 , 33 , 113 , … 3, 13, 23, 33, 113, \ldots 3,13,23,33,113,… in ascending order. For example, 113 113 113 can be expressed as 113 = 1 + 1 + 111 113 = 1 + 1 + 111 113=1+1+111.
Note that the three repunits do not have to be distinct.
Sample Input 2
19
Sample Output 2
2333
Sample Input 3
333
Sample Output 3
112222222233
Solution
具体见文后视频。
Code
#include D - Erase Leaves
Problem Statement
You are given a tree with N N N vertices: vertex 1 , 1, 1, vertex 2 2 2, … \ldots …, vertex N N N.
The i i i-th edge ( 1 ≤ i < N ) (1\leq i\lt N) (1≤i<N) connects vertex u i u _ i ui and vertex v i v _ i vi.
Consider repeating the following operation some number of times:
Choose one leaf vertex v v v and delete it along with all incident edges.
Find the minimum number of operations required to delete vertex 1 1 1.
2 ≤ N ≤ 3 × 1 0 5 2\leq N\leq3\times10^5 2≤N≤3×105
1 ≤ u i < v i ≤ N ( 1 ≤ i < N ) 1\leq u _ i\lt v _ i\leq N\ (1\leq i\lt N) 1≤ui<vi≤N (1≤i<N)
The given graph is a tree.
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N
u 1 u _ 1 u1 v 1 v _ 1 v1
u 2 u _ 2 u2 v 2 v _ 2 v2
⋮ \vdots ⋮
u N − 1 u _ {N-1} uN−1 v N − 1 v _ {N-1} vN−1
Output
Print the answer in a single line.
Sample Input 1
9
1 2
2 3
2 4
2 5
1 6
6 7
7 8
7 9
Sample Output 1
5
The given graph looks like this:

For example, you can choose vertices 9 , 8 , 7 , 6 , 1 9,8,7,6,1 9,8,7,6,1 in this order to delete vertex 1 1 1 in five operations.
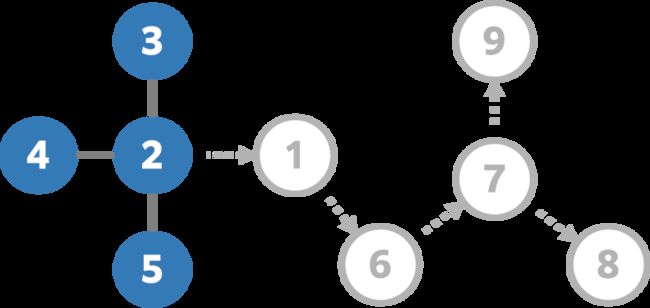
Vertex 1 1 1 cannot be deleted in four or fewer operations, so print 5 5 5.
Sample Input 2
6
1 2
2 3
2 4
3 5
3 6
Sample Output 2
1
In the given graph, vertex 1 1 1 is a leaf.
Hence, you can choose and delete vertex 1 1 1 in the first operation.
Sample Input 3
24
3 6
7 17
7 20
7 11
14 18
17 21
6 19
5 22
9 24
11 14
6 23
8 17
9 12
4 17
2 15
1 17
3 9
10 16
7 13
2 16
1 16
5 7
1 3
Sample Output 3
12
Solution
具体见文后视频。
Code
#include E - Takahashi Quest
Problem Statement
Takahashi will embark on an adventure.
During the adventure, N N N events will occur.
The i i i-th event ( 1 ≤ i ≤ N ) (1\leq i\leq N) (1≤i≤N) is represented by a pair of integers ( t i , x i ) (t _ i,x _ i) (ti,xi) ( 1 ≤ t i ≤ 2 , 1 ≤ x i ≤ N ) (1\leq t _ i\leq 2,1\leq x _ i\leq N) (1≤ti≤2,1≤xi≤N) and is as follows:
If t i = 1 t _ i=1 ti=1, he finds one potion of type x i x _ i xi. He can choose to pick it up or discard it.
If t i = 2 t _ i=2 ti=2, he encounters one monster of type x i x _ i xi. If he has a potion of type x i x _ i xi, he can use one to defeat the monster. If he does not defeat it, he will be defeated.
Determine whether he can defeat all the monsters without being defeated.
If he cannot defeat all the monsters, print -1.
Otherwise, let K K K be the maximum number of potions he has at some point during the adventure.
Let K min K _ {\min} Kmin be the minimum value of K K K across all strategies where he will not be defeated.
Print the value of K min K _ {\min} Kmin and the actions of Takahashi that achieve K min K _ {\min} Kmin.
Constraints
1 ≤ N ≤ 2 × 1 0 5 1\leq N\leq2\times10^5 1≤N≤2×105
1 ≤ t i ≤ 2 ( 1 ≤ i ≤ N ) 1\leq t _ i\leq2\ (1\leq i\leq N) 1≤ti≤2 (1≤i≤N)
1 ≤ x i ≤ N ( 1 ≤ i ≤ N ) 1\leq x _ i\leq N\ (1\leq i\leq N) 1≤xi≤N (1≤i≤N)
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N
t 1 t _ 1 t1 x 1 x _ 1 x1
t 2 t _ 2 t2 x 2 x _ 2 x2
⋮ \vdots ⋮
t N t _ N tN x N x _ N xN
Output
If Takahashi cannot defeat all the monsters, print -1.
If he can, print the value of K min K _ {\min} Kmin in the first line, and in the second line, for each i i i such that t i = 1 t _ i=1 ti=1 in ascending order, print 1 if he picks up the potion found at the i i i-th event, and 0 otherwise, separated by spaces.
If multiple sequences of actions achieve K min K _ {\min} Kmin and allow him to finish the adventure without being defeated, you may print any of them.
Sample Input 1
13
1 2
1 3
1 1
1 3
1 2
2 3
1 3
1 3
2 3
1 3
2 2
2 3
2 1
Sample Output 1
3
1 1 1 0 0 1 0 1
The sample output corresponds to the following actions:
Find potions of types 2 , 3 , 1 2,3,1 2,3,1 in this order. Pick up all of them.
Find potions of types 3 , 2 3,2 3,2 in this order. Do not pick up any of them.
Encounter a type- 3 3 3 monster. Use one type- 3 3 3 potion to defeat it.
Find a type- 3 3 3 potion. Pick it up.
Find a type- 3 3 3 potion. Do not pick it up.
Encounter a type- 3 3 3 monster. Use one type- 3 3 3 potion to defeat it.
Find a type- 3 3 3 potion. Pick it up.
Encounter a type- 2 2 2 monster. Use one type- 2 2 2 potion to defeat it.
Encounter a type- 3 3 3 monster. Use one type- 3 3 3 potion to defeat it.
Encounter a type- 1 1 1 monster. Use one type- 1 1 1 potion to defeat it.
In this sequence of actions, the value of K K K is 3 3 3.
There is no way to avoid defeat with K ≤ 2 K\leq 2 K≤2, so the sought value of K min K _ {\min} Kmin is 3 3 3.
There are multiple sequences of actions that satisfy K = 3 K=3 K=3 and allow him to avoid defeat; you may print any of them.
Sample Input 2
4
2 3
1 4
2 1
1 2
Sample Output 2
-1
He will inevitably be defeated by the first monster he encounters.
Sample Input 3
30
1 25
1 2
1 10
1 18
2 18
1 11
2 11
1 21
1 6
2 2
2 10
1 11
1 24
1 11
1 3
1 2
1 18
2 25
1 8
1 10
1 11
2 18
2 10
1 10
2 2
1 24
1 10
2 10
1 25
2 6
Sample Output 3
4
1 1 1 1 1 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0
Solution
具体见文后视频。
Code
#include F - Bomb Game 2
Problem Statement
There are N N N people standing in a line, with person i i i standing at the i i i-th position from the front.
Repeat the following operation until there is only one person left in the line:
Remove the person at the front of the line with a probability of 1 2 \frac{1}{2} 21, otherwise move them to the end of the line.
For each person i = 1 , 2 , … , N i=1,2,\ldots,N i=1,2,…,N, find the probability that person i i i is the last person remaining in the line, modulo 998244353 998244353 998244353. (All choices to remove or not are random and independent.)
2 ≤ N ≤ 3000 2\leq N\leq 3000 2≤N≤3000
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N
Output
Print the answer for people i = 1 , 2 , … , N i=1,2,\ldots,N i=1,2,…,N, separated by spaces.
Sample Input 1
2
Sample Output 1
332748118 665496236
Person 1 1 1 will be the last person remaining in the line with probability 1 3 \frac{1}{3} 31.
Person 2 2 2 will be the last person remaining in the line with probability 2 3 \frac{2}{3} 32.
Sample Input 2
5
Sample Output 2
235530465 792768557 258531487 238597268 471060930
Solution
具体见文后视频。
Code
#include 视频题解
Atcoder Beginner Contest 333 讲解
最后祝大家早日![]()