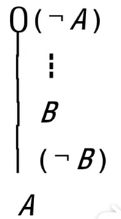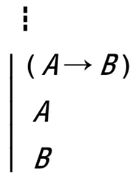【清华大学】《逻辑学概论》笔记
教学视频来源
| - | - | - |
|---|---|---|
| - | 第0讲 概要 | - |
| 0.1 讲师介绍 | 0.2 课程内容 | - |
| - | 第1讲 什么是逻辑学？ | - |
| 1.1 “逻辑和逻辑学 | 1.2 推理和推理形式 | 1.3 有效推理形式 |
| 1.4 逻辑学的特点 | 1.5 逻辑学的基本准则 | 1.6 逻辑学和其他学科的关系 |
| 1.7 关于本课程《逻辑学概论》 | - | - |
| - | 第2讲 逻辑学的产生与发展 | - |
| 2.1 中国古代逻辑思想（上） | 2.2 中国古代逻辑思想（中） | 2.3 中国古代逻辑思想（下） |
| 2.4 印度古代逻辑 | 2.5 古希腊和中世纪逻辑 | 2.6 近代西方逻辑 |
| 2.7 数理逻辑的提出和实现 | 2.8 数理逻辑的发展 | - |
| - | 第3讲 命题联结词及其基本推理形式 | - |
| 3.1 推理和命题 | 3.2 基本命题和复合命题 | 3.3 常用命题联结词及其基本推理形式（1） |
| 3.4 常用命题联结词及其基本推理形式（2） | 3.5 常用命题联结词及其基本推理形式（3） | 3.6 常用命题联结词及其基本推理形式（4） |
| 3.7 常用命题联结词及其基本推理形式（5） | 3.8 常用命题联结词及其基本推理形式（6） | 3.9 常用命题联结词及其基本推理形式（7） |
| - | 第4讲 复合命题的推理：有效推理形式的判定 | - |
| 4.1 重言式、矛盾式和可满足式 | 4.2 具体推理转换为推理形式 | 4.3 推理形式转换为复合命题形式 |
| 4.4 有效推理形式的判定：真值表法 | 4.5 有效推理形式的判定：归谬赋值法 | - |
| - | 第5讲 复合命题的推理：命题联结词的充足集 | - |
| 5.1 命题联结词：真值函数 | 5.2 析取范式 | 5.3 为复合命题形式作与之等值的析取范式 |
| 5.4 合取范式 | 5.5 范式存在定理 | 5.6 命题联结词的充足集 |
| 5.7 命题联结词的独元充足集 | - | - |
| - | 第6讲 命题演算：公理系统 | - |
| 6.1 公理系统的构成 | 6.2 命题演算的公理系统L | 6.3 命题演算公理系统L中的证明 |
| 6.4 命题演算公理系统L中的证明（续） | 6.5 命题演算公理系统L中的推演 | - |
| - | 第7讲 命题演算：公理系统，自然演绎系统 | - |
| 7.1 公理系统出发点的延伸 | 7.2 公理系统的评价 | 7.3 公理系统的性质和评价及其意义 |
| 7.4 命题演算的自然演绎系统 | 7.5 命题演算自然演绎系统中的证明和推演 | - |
| - | 第8讲 基本命题的构成 | - |
| 8.1 基本命题的结构 | 8.2 词项的内涵和外延 | 8.3 词项的种类 |
| 8.4 词项间的关系 | 8.5 词项的定义 | 8.6 词项的划分 |
| 8.7 谓词的分类 | 8.8 量词 | 8.9 联词 |
| - | 第9讲 传统逻辑中基本命题的推理 | - |
| 9.1 基本命题的推理 | 9.2 传统逻辑对基本命题的分析 | 9.3 性质命题中主、谓词的周延 |
| 9.4 命题变形的推理 | 9.5 根据对当关系的推理 | 9.6 三段论 |
| 9.7 三段论的式与格 | 9.8 有效三段论的判定 | - |
| - | 第10讲 基本命题的推理 | - |
| 10.1 性质命题 | 10.2 主词非空的预设 | 10.3 关系命题的结构 |
| 10.4 关系命题根据量词的推理 | 10.5 关系命题根据谓词性质的推理方法 | 10.6 谓词演算简介 |
| - | 第11讲 非经典逻辑的初步 | - |
| 11.1 非经典（非标准）逻辑 | 11.2 多值逻辑 | 11.3 模糊逻辑 |
| 11.4 模态逻辑 | 11.5 规范逻辑 | 11.6 时态逻辑 |
| 11.7 弗协调逻辑 | - | - |
| - | 第12讲 余论 | - |
| 12.1 演绎和归纳 | 12.2 探求因果关系的逻辑方法 | 12.3 证论和反驳 |
| 12.4 悖论 | 12.5 本课程《逻辑学概论》内容回顾 | - |
第0讲 概要
0.1 讲师介绍
陈为蓬 清华大学人文学院 副教授
0.2 课程内容
- 第1讲 什么是逻辑学？
- 第2讲 逻辑学的产生与发展
- 第3讲 命题联结词及其基本推理形式
- 第4讲 复合命题的推理：有效推理形式的判定
- 第5讲 复合命题的推理：命题联结词的充足集
- 第6讲 命题演算：公理系统
- 第7讲 命题演算：公理系统，自然演绎系统
- 第8讲 基本命题的构成
- 第9讲 传统逻辑中基本命题的推理
- 第10讲 基本命题的推理
- 第11讲 非经典逻辑的初步
- 第12讲 余论
第1讲 什么是逻辑学？
1.1 “逻辑和逻辑学
什么是逻辑？
“逻辑”一词的多种用法:
- “事物发展有其内在的逻辑。”
- “这个人为人处世，有他自己的逻辑。”
- “按照对方辩友的逻辑，岂不是说…？”
帝国主义者的逻辑和人民的逻辑是这样的不同。捣乱，失败，再捣乱，再失败，直至灭亡————这就是帝国主义和世界上一切反动派对待人民事业的逻辑，他们决不会违背这个逻辑的。…斗争，失败，再斗争，再失败，再斗争，直至胜利一这就是人民的逻辑，他们也是决不会违背这个逻辑的。 ————(毛泽东:《丢掉幻想准备斗争》)
上面的逻辑与逻辑学中的逻辑相差甚远，上面更多的是客观规律，行为方式。
“逻辑”一词的另多种用法:
- “说话、写文章都要讲逻辑。”
- “这篇论文结构严谨，逻辑严密。”
- “他的发言颠三倒四，逻辑混乱。”
上面的逻辑与逻辑学中的逻辑比较接近，但仍然不是逻辑学中研究对象。
逻辑(logic)一词的语源
- 来自希腊语logos (逻各斯) :
- 世界的可理解的规律;
- 一般的原理和规则;
- 语言、命题、说明、解释、论证;
- 理性、理念、推理、推理能力;
- 尺度、关系、比例、价值;
“逻辑”一词的不同含义:
- 客观事物的规律性;
- 某种理论、观点、行为方式;（比如上面毛主席的话）
- 思维的规律、规则;（比如文章复合逻辑）
- 一门学科，即逻辑学。
逻辑学：以推理形式为主要研究对象的学科（要与日常中逻辑区分开来）
1.2 推理和推理形式
推理：从已知条件(前提)得出结论的过程
例如，侦破案件步骤:
- 提取材料
- 搜集条件
- 得出结论
侦破案件是一个推理过程
又例如，法庭审案根据案卷（关于案件的材料、已知条件），作出判罚，这也是推理过程。
又例如，数学上证明定理：用公理、定理推出新定理，这也是推理过程。
我们日常生活中，不经意都会推理（例如，父母回到家，摸电视背后，感觉有没有发烫，判断小孩在自己进门前是否在观看电视）
推理形式:推理的结构
同类的不同具体推理具有共同的结构，即推理形式。
- 所有金属都是导体，铜是金属 -> 铜是导体
- 所有鸟都是卵生的，企鹅是鸟 -> 企鹅是卵生的
- 所有A都是B，C是A -> C是B（共同的结构）
1.3 有效推理形式
-
所有金属都是导体，铜是金属 -> 铜是导体（正确）
-
所有A都是B，C是A -> C是B（有效推理形式）
-
所有金属都是导体，铜是导体 -> 铜是金属（不正确）（反例：碳是导体）
-
所有A都是B，C是B -> C是A（无效推理形式）
有效推理形式
- 真前提通过有效推理形式只能得到真结论。
- 即:通过有效推理形式，从真前提不会得到假结论。
逻辑：研究推理、推理形式
1.4 逻辑学的特点
- 抽象性
- 应用性
- 工具性
所有的科学在某种意义上都是某一方面的抽象
数理逻辑的公理系统中：符号只是符号本身，具有非常高的抽象性（也就是具有广泛应用性）
逻辑是一门高度抽象的学科，应用范围广。
欧姆定理 U = IR，通过实验得出。之后可用数学求出，可不再用实验求其中某一值。
数学是物理学和很多学科的工具。逻辑学也一样。
- 因A=B，故B=A 对
- 因A>B，故B>A 错
- 因A!=B，故B!=A 对
显然它们是正确，但“显然”不靠谱。在逻辑学上，若两对象关系是对称的，则位置可互换，否则，不行。
- 由A=B和B=C，可得A=C。
显然这是正确。在逻辑学上，等于号=具有传递的关系
1.5 逻辑学的基本准则
逻辑学研究对象范围很小：推理以及与推理有关的问题。
逻辑学的基本准则：
- 同一律 A就是A（譬如，跑题）
- （不）矛盾论 不矛盾论就是矛盾律，A不是非A，A和A的否定不能同时成立
- 排中律：A或A的否定必有一真，也就是没有中间态
矛盾论：A和A的否定不能同时成立，但是日常生活中，常常描述某事物同时是好是坏，如这事物指下雪。
正确的解读：
-
A：下雪是好事
-
A的否定：下雪是坏事
-
A1：下雪对冬小麦是好事
-
A2的否定：下雪对交通是坏事
A与A1是不同的
同一律，（不）矛盾论普遍适用
而排中律的适用范围是没有中间状态的，而二者互补的
例子：
- 张三是男生，张三是女生，违反矛盾论
- 张三不是男生，张三不是女生，违反排中律
日常生活中，符不符合逻辑，往往就逻辑学的基本准则几方面而言的。
1.6 逻辑学和其他学科的关系
逻辑学与以下学科的关系密切
- 哲学
- 数学
- 语言学
- 计算机科学
逻辑学最早是作为哲学的一部分存在的。
哲学，狭义理解，主要解决世界本原问题，物质的，还是精神的，是主观的，还是客观的。
本体论和认识论是哲学的核心。
广义理解，包括逻辑学，伦理学，美学
数理逻辑：用数学的方法、数学的语言、数学的工具研究推理。数理逻辑的成果为数学基础的研究服务。
语言是逻辑的外壳
语文老师会认为“整个大楼片漆黑，只有那个窗户灯火通明。”是不对的，因为这两个子句互为矛盾
同样，“中国有着世界上任何国家都没有的万里长城”也是不对的。
计算机科学 离散数学
最早的逻辑系统：二值，是与不是
推理：演绎和归纳
- 演绎：从一般到个别
- 归纳：从个别到一般
计算机为未做到归纳，但能做到演绎
归纳逻辑它的一个任务是要把我们所做的具体的归纳，要给出归纳的有效推理形式。
1.7 关于本课程《逻辑学概论》
传统逻辑还是数理逻辑？
- 传统逻辑：古典逻辑 古希腊亚里士多德为代表。
- 数理逻辑：现代逻辑 西方以莱布尼茨为创始人。
课程内容：数理逻辑的基础部分和传统逻辑的常用部分。
数理逻辑：不涉及任何一门高等数学的具体内容。
通过具体的推理了解:逻辑的精神、逻辑的方法、逻辑的思路。
第2讲 逻辑学的产生与发展
2.1 中国古代逻辑思想（上）
逻辑学的产生和发展
了解逻辑学的思路、精神、方法
世界三大逻辑传统：
- 中国
- 印度
- 希腊
中国先秦时代的逻辑思想：春秋战国，百家争鸣
中国古代逻辑思想不像希腊那样单纯研究推理，而是渗透在，贯穿在对于其他许多问题的研究与论述当中。
孔子为主要代表
子日：觚不觚，觚哉!觚哉!————《论语.雍也篇》（觚：用来喝酒的青铜具）
子日：必也正名乎! …名不正则言不顺，言不顺则事不成，事不成则礼乐不兴，礼乐不兴则刑罚不中，刑罚不中则民无所措手足。故君子名之必可言也，言之必可行也。————《论语.子路篇》（推理）
白马非马
日：“马非马，可乎?”
日：“可。”
日：“何哉?”
日: “马者所以命形也。白者所以命色也。命色者非命形也，故日白马非马。”…
日：“求马，黄、黑马皆可致。求白马，黄、黑马不可致。”
————公孙龙子《白马论》
- 传统逻辑：日常语言
- 数理逻辑：人工语言
例如日常语言的“是”有多种含义（“白马非马”的例子），需要更精准语言进行描述
2.2 中国古代逻辑思想（中）
庄子与惠子游于濠梁之上。庄子日：“鲦鱼出游从容，是鱼之乐也。”
惠子日：“子非鱼，安知鱼之乐？”（安：哪里？怎么？惠子的“安”是指“怎么”）
庄子日：“子非我，安知我不知鱼之乐？”
惠子日：“我非子，固不知子矣;子固非鱼也，子之不知鱼之乐，全矣。”
庄子日：“请循其本。子日‘汝安知鱼乐’云者，既已知吾知之而问我，我知之濠上也。”（庄子以“安”作为“哪里”进行回答，违反逻辑学的基本准则的同一律）
————《庄子.外篇.秋水第十七》
楚人有鬻盾与矛者，誉之日:“吾盾之坚，物莫能陷也。”又誉其矛日：“吾矛之利，于物无不陷也。”或日，“以子之矛陷，子之盾何如？”其人弗能应也。
不可陷之盾与无不陷之矛，不可同世而立。（说明矛盾律的原理）
————《韩非子.难一》
2.3 中国古代逻辑思想（下）
类比（濠梁之辩），递推（孔子的正名）作为推理手段
墨家
前期墨家:墨家创始人墨翟(墨子，约公元前476-前390)本人在世时所组成的学派。
后期墨家:墨翟去世后由其弟子所组成的学派。
《墨子》：《墨经》(《墨辩》)
《墨经》：经上、经下、经说上、经说下、大取、小取。
知识的来源:亲知（我直接感受到的），闻知（别人告诉我的），说知（这的“说”是指推理）。
知识的内容:名知（如知道梧桐树的名字），实知（如知道梧桐树的具体事物），合知（如知道梧桐树的名字和它具体事物），为知（实践，如怎么保护它）。
提出比较完整的逻辑体系，但不是逻辑学的名著。
夫辩者，将以明是非之分，审治乱之纪，明同异之处，察名实之理，处利害，决嫌疑焉。（推理很重要）
以名举实，以辞抒意，以说出故。
————《墨经.小取》
- 以名举实：用不同的名去对应不同的实（概念）。（命题）
- 以辞抒意：用句子表达一个意思。（判断）
- 以说出故：用推理可以知道事物的原因。（推理）
为什么逻辑学主要在先秦时期发展？百家争鸣
后秦时期主要以儒家思想为主（怎么修身齐家治国平天下，也就是社会科学和人文科学方面比较看重），逻辑学没有太大的成就。
2.4 印度古代逻辑
古代论辩术(公元前5世纪一前3世纪)
正理论
因明
佛教逻辑:因明
- 创始人:龙树(约2-3世纪间)
- 陈那(约425-495) :开创新因明，《因明正理门论》、《集量论》
- 商羯罗主(5世纪):《因明入正理论》
- 宗，因，喻
佛教有五明：
- 声明
- 医方明
- 因明
- 内明
- 工巧明
因明的三支论式
- 宗:此山有火
- 因:因有烟故
- 喻:凡有烟均有火，如厨房(同喻)。凡无烟均无火，如湖(反喻)。
古五支论式：宗、因、喻、合、结
因明的东传
- 玄奘(约600-664)：
- 提出“唯识比量，（“直唯识量”）；
- 翻译《因明正理门论》、《因明入正理论》。
2.5 古希腊和中世纪逻辑
代表：苏格拉底、帕拉图、亚里士多德
亚里士多德 Aristoteles(公元前384-前322 ) 古希腊逻辑集大成者，逻辑学之父
《工具论》:范畴篇、解释篇、前分析篇、后分析篇、论辩篇、辨谬篇
三段论理论等
三段论
如：所有的金属是导体，铜是金属 -> 铜是导体
麦加拉——斯多阿学派逻辑：构造了命题逻辑系统、构造公理系统
命题逻辑：如果铜是金属，那么铜是导体
继承发展古希腊和阿拉伯的逻辑思想，建立经院逻辑体系
2.6 近代西方逻辑
归纳逻辑
培根 Francis Bacon ( 1561-1626 ) :
《新工具》：发现(归纳)，思想(演绎)，记忆，传递（授）
归纳方法:三表法一一出现表(具有表)，不出现表(缺乏表)，程度表(比较表)
三段论：所有人固有一死，苏格拉底是人，所以苏格拉底会死。
有效推理形式：只要前提对，结论就一定对
他认为三段论是演绎（从一般到个别），不能从中得到新东西，但归纳可以。
你怎么知道所有人固有一死，但你得知苏格拉底、柏拉图等人都死了，可推出人固有一死，这个过程称为归纳。
密尔(穆勒) John Stuart Mill ( 1806-1873 ) : 求因果五法
辩证逻辑
康德 I. Kant ( 1724- - 1804 ) 《纯粹理性批判》 先验逻辑
黑格尔G.W.F.Hegel ( 1770-1831 ) 《逻辑学》 思想范畴的辩证发展
2.7 数理逻辑的提出和实现
莱布尼茨Leibniz ( 1646-1716 ) : 《论组合术》
- 提出关于数理逻辑的思想，设想建立“普遍的符号语言”（减少传统逻辑的多义，歧义所带来争论）：
- 思想的字母
- 思维的演算
数理逻辑：数学逻辑 mathematical logic（不是数学与物理）
布尔G.Boole ( 1815-1864 ) : 《逻辑的数学分析》、《思维规律的研究》 创立逻辑代数，实现逻辑演算(命题演算)
布尔代数无法解决三段论（布尔代数不含量词（全部，有些））部分实现逻辑的演算。
德.摩根 De Morgan ( 1806-1871):
- 《形式逻辑》、《论三段论III和一般逻辑》、《论三段论IV和关系逻辑》
- 创建关系逻辑
关系逻辑：
- 5 > 3, 3 > 2，所以5 > 2
- 上海在北京的南边，广州在上海的南边，所以广州在北京的南边
两个东西的关系，用自然语言是说得清的，但两类东西之间的关系，加上量词的话，就可能会说不清楚。
比如锅比盆大，是所有锅比所有盆大，还是有些锅比所有盆大，还是…
再比如，盆大小在碗和盆的之间，是所有…好累（我笑了）
弗雷格 G.Frege ( 1848-1925 ) :《概念文字》 引入量词，实现谓词演算
罗素B.Russell ( 1872- -1970) :
- 《数学原理》(1910-1913) ,合作者:怀特海A.N.Whitehead ( 1861-1947 )
- 建立完备的命题演算和谓词演算，成为逻辑演算的经典系统
2.8 数理逻辑的发展
- 逻辑演算(命题演算、谓词演算)
- 证明论
- 集合论(公理集合论和素朴集合论)
- 递归论
- 模型论
希尔伯特Hilbert ( 1862-1943 )、哥德尔Godel ( 1906-1978 )、图灵Turing ( 1912-1954 )、塔尔斯基Tarski ( 1902-1983 )等人的贡献
逻辑演算：命题演算，谓词演算 两个演算
四论：证明论、集合论、递归论、模型论
数理逻辑内容：两个演算，四论
非经典逻辑(非标准逻辑)的出现：
经典逻辑(标准逻辑)：以罗素、怀特海《数学原理》为代表
非经典逻辑(非标准逻辑)：多值逻辑（不止有真假值），模糊逻辑，模态逻辑（一定，不一定），广义模态逻辑（有时，永远），弗协调逻辑（例外，动摇经典逻辑，可另建其他系统）
经典逻辑的系统是非经典逻辑系统的子系统。
第3讲 命题联结词及其基本推理形式
3.1 推理和命题
推理：从前提(已知条件)得出结论的过程。
推理的前提和结论都是命题。
命题：对事物及其情况(性质、关系)的陈述。
- 如北京是一个大城市。（性质）（什么东西怎么样）
- 如张三和李四是同班同学。（关系）
命题的真值：命题的真假情况。
每一个命题都有真值，这是命题的基本性质
命题是一种陈述，命题是一种句子。句子不一定是命题。命题一定是用句子的形式表达。
命题：今天这里下雨。命题一定是说，什么东西，怎么样。
一个句子，只要客观上有真假，那么这就是一个命题。（命题如：火星上有生物）
有效推理形式:真前提通过有效推理形式只能得到真结论。
即: 通过有效推理形式，真前提不会得到假结论。
3.2 基本命题和复合命题
基本命题：本身不再包含其他命题的命题。
复合命题：由一个或多个基本命题加上命题联结词所构成的命题。
基本命题：
- 今天下雨。
- 今天刮风。
复合命题：
- 今天下雨，并且今天刮风。
基本命题和复合命题其真值的确定:
- 基本命题的真值：逻辑学本身不能确定其所陈述的孤立的基本命题的真值。
- 复合命题的真值：由作为其组成部分的基本命题之真值和相关的命题联结词之性质所共同决定。
- 对某些有特定结构的复合命题，逻辑学本身即可确定其真或假。
互相否定的两个命题是不能同时成立的。（矛盾律）
复合命题的真值判定的例子：
今天下雨。 假
今天刮大风。 真
今天下雨，并且今天刮大风。 假
逻辑不能确定基本命题的真假。
逻辑参与确定复合命题的真假。
对于某些有特定结构的复合命题，逻辑可以独立地确定它的真和假。
逻辑学研究的不是具体的命题，而是同类的具体俞题所共同具有的命题形式，即命题结构。
命题形式用一定的符号表示。如：以特定符号表示不同的命题连接词，而以p表示基本命题。（命题：proposition )
3.3 常用命题联结词及其基本推理形式（1）
这里将给出各命题联结词的名称、符号、真值表、基本推理形式。
真值表：显示命题形式在各种可能情况下的真值。
在真值表中，通常以P1 ,P2, P3, … 或p,q,r,…表示基本命题，以T表示真(true) ，以F表示假(false)。
常用命题联结词：
（1）否定：¬
真值表：
| p | ¬p |
|---|---|
| T | F |
| F | T |
基本推理形式：双重否定式¬(¬p) -> p
自然语言的否定往往带有其他感情色彩，而逻辑学的否定是纯粹的，所以，它们不完全对等。
如：我们不得不学习英语。
3.4 常用命题联结词及其基本推理形式（2）
（2）合取：∧
| p | q | p∧q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
自然语言中的“而且”有递进的意思。我毕了业，而且考上研究生。若换成，我考上研究生，而且毕了业。
虽然…但是…也是类似道理，逻辑学的合取意思纯粹。
基本推理形式：
- 构成式 p,q -> p∧q。
p：他数学成绩不错，q：他英语成绩也不错。p∧q：他的数学和英语不错
- 分解式
p∧q -> p, p∧q -> q
- 异位式
p∧q <-> q∧p
合取的推广
| p | q | r | p∧q∧r |
|---|---|---|---|
| T | T | T | T |
| T | T | F | F |
| T | F | T | F |
| T | F | F | F |
| F | T | T | F |
| F | T | F | F |
| F | F | T | F |
| F | F | F | F |
3.5 常用命题联结词及其基本推理形式（3）
（3）析取 ∨
| p | q | p∨q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
基本推理形式：
- 构成式 p -> p∨q。p真，p∨q真
- 异位式 p∨q <-> q∨p
- 否定肯定式 p∨q, ¬p -> q
例如，李四和张三同为嫌疑犯，后确定不是李四干的，所以张三是法外狂徒。
析取的推广
| p | q | r | p∨q∨r |
|---|---|---|---|
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F | T |
| F | T | T | T |
| F | T | F | T |
| F | F | T | T |
| F | F | F | F |
3.6 常用命题联结词及其基本推理形式（4）
（4）不相容析取：∀
| p | q | p∀q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
基本推理形式：
- 肯定否定式 p∀q, p -> ¬q
- 否定肯定式 p∀q, ¬p -> q
(p∀q) 与 (p∨q)∧(¬(p∧q))真值相同。
- 不是张三就是李四作案。
- 张三或李四作案 且 张三和李四不会一同作案
3.7 常用命题联结词及其基本推理形式（5）
（5）蕴涵：➝
| 序号 | p | q | p➝q |
|---|---|---|---|
| 1 | T | T | T |
| 2 | T | F | F |
| 3 | F | T | T |
| 4 | F | F | T |
- 如果…那么…
- 若…则…
- 一…就…
蕴涵相当于充分条件，但不等于
例如，如果2+2=4，那么雪是白的。（在自然语言中它们没有内在联系，通常是不允许的。而在逻辑学上可以）
“蕴涵怪论”：
- 假命题蕴涵任何命题（看上表3、4）
- 任何命题蕴涵真命题（看上表1、3）
看起来很怪
举个例子：
| p：比赛输了 | q：我请客 | p➝q：我信用好 |
|---|---|---|
| T | T | T（兑现承诺） |
| T | F（我没请客） | F（我信用差） |
| F（比赛赢了） | T（我请客） | T（我是好人） |
| F | F | T |
基本推理形式：
- 肯定前件式 p➝q, p -> q（我信用很好，比赛输了->我请客）
- 否定后件式 p➝q, ¬q -> ¬p（我信用很好，我没有请客->比赛赢了）
- 异位式 p➝q -> (¬q)➝(¬p)（比赛输了➝我请客 -> 我没请客➝比赛赢了）
- 连锁式
- p➝q, q➝r -> p➝r
- p➝q, q➝r -> (¬r)➝(¬p)
- p➝q, q➝r, r➝s -> p➝r（小孩一考试就紧张，一紧张就考砸，一考砸就被双亲混合双打 -> 小孩一考试就挨打）
- p➝q, q➝r, r➝s -> (¬s)➝(¬p)（小孩一考试就紧张，一紧张就考砸，一考砸就被双亲混合双打 -> 小孩没挨打，最近没考试）
3.8 常用命题联结词及其基本推理形式（6）
（6）反蕴涵 ⟵
| p | q | p⟵q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | F |
| F | F | T |
反蕴涵在汉语里面常用的说法比较少，典型的只有一个：只有…才…，表示相当于必要条件。
在汉语中，命题连接词是没有出现，而且有的看起来是相同的情况，但它所对应的这个命题连接词有时候不一样的，比如：
- 不吃不喝（合取）
- 不去不行（蕴涵）
| p | q | p⟵q | 例子 |
|---|---|---|---|
| T | T | T | 只有天气好才去爬山 真 |
| T | F | T | 天气好我没有爬山 真 |
| F | T | F | 天气不好我去爬山 假 |
| F | F | T | 天气不好，我没去爬山 真 |
- 蕴涵：前真 后假 是假的
- 反蕴涵：前假 后真 是假的
基本推理形式：
- 肯定后件式 p⟵q, q -> p（只有天气好才去爬山，我爬山了 -> 天气好）
- 否定前件式 p⟵q, ¬p -> ¬q（只有天气好才去爬山，天气不好 -> 我没爬山）
（p⟵q）与（q➝p）真值相同。
3.9 常用命题联结词及其基本推理形式（7）
（7）等值：⟷
| p | q | p⟷q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
等值的在日常的说法为当且仅当，它相当于充分必要条件（注意，它们不完全一样，用可以是一样）
基本推理形式：
-
构成式
- p➝q, p⟵q -> p⟷q
- p➝q, p➝q -> p⟷q
-
分解式
- p⟷q -> p➝q
- p⟷q -> p⟵q
-
异位式
- p⟷q -> q⟷p
p⟷q
- 肯定前件式
- 肯定后件式
- 否定前件式
- 否定后件式
- 连锁式
都成立
(p⟷q)与((p➝q)∧(q➝p))真值相同
常用命题连接词的真值表
| p | q | ¬p | p∧q | p∨q | p∀q | p➝q | p⟵q | p⟷q |
|---|---|---|---|---|---|---|---|---|
| T | T | F | T | T | F | T | T | T |
| T | F | F | F | T | T | F | T | F |
| F | T | T | F | T | T | T | F | F |
| F | F | T | F | F | F | T | T | T |
∀, ⟵,⟷ 可被∧, ∨, ¬q取代
与上表可以精简成为：
| p | q | ¬p | p∧q | p∨q | p➝q |
|---|---|---|---|---|---|
| T | T | F | T | T | T |
| T | F | F | F | T | F |
| F | T | T | F | T | T |
| F | F | T | F | F | T |
第4讲 复合命题的推理：有效推理形式的判定
4.1 重言式、矛盾式和可满足式
根据可能的真值情况，命题形式可分为:
- 重言式(tautology)(永真式) 在任何情况下，其真值永远为真。
- 矛盾式(contradiction) (永假式)
- 可满足式(satisfaction)
重言式(tautology)(永真式)(同义反复)在任何情况下，其真值永远为真。如：p∨(¬q)，p➝p
今天下雨或今天不下雨。
可用真值表判定。
| p | ¬p | p∨(¬p) |
|---|---|---|
| T | F | T |
| F | T | T |
| p | p➝p |
|---|---|
| T | T |
| F | T |
矛盾式(contradiction)(永假式)在任何情况下，其真值永远为假。
| p | ¬p | p∧(¬p) |
|---|---|---|
| T | F | F |
| F | T | F |
可满足式(satisfaction)在某些情况下，其真值为真，而在某些情况下，其真值为假。
| p | ¬p |
|---|---|
| T | F |
| F | T |
任何孤立的命题都是可满足式。
4.2 具体推理转换为推理形式
并非今天不是节日 -> 今天是节日
¬(¬p) -> p
复合命题推理
- 若今天星期二则今天有课，今天是星期二 -> 今天有课 | p➝q, p -> q
- 若今天星期二则今天有课，今天是星期二 -> 今天有课
- 若今天星期二则今天有课，今天不是星期二 -> 今天没课
- 若今天星期二则今天有课，今天不是星期二 -> 今天没课 | p➝q, ¬p -> ¬q
具体推理转换为推理形式:
用逻辑符号(命题变元即基本命题符号、命题联结词符号及括号)把自然语言推理中的前提和结论写成命题形式，从而形成推理形式。
4.3 推理形式转换为复合命题形式
（前提）¬(¬p) -> （结论）p
| 推理形式 | 复合命题形式 |
|---|---|
| （前提）p➝q, （前提）¬q -> （结论）¬p | ((p➝q)∧(¬q))➝(¬q) |
推理形式转换为命题形式：用蕴涵、合取符号及括号把推理形式转换为复合命题形式。
4.4 有效推理形式的判定：真值表法
有效推理形式所对应的复合命题形式当且仅当是重言式。
因此，对一个复合命题推理形式是否有效的判定，转化为对一个复合命题形式是否为重言式的判定。
推理形式：¬(¬p) -> p，复合命题形式：¬(¬p) ➝ p，用真值表进行判定推理形式有效性。
| p | ¬p | ¬(¬p) | ¬(¬p)➝p |
|---|---|---|---|
| T | F | T | T |
| F | T | F | T |
再比如
推理形式：p➝q, ¬q -> ¬p，复合命题形式：((p➝q)∧(¬q))➝(¬p)
((p➝q)∧(¬q))➝(¬p)的真值表：
| p | q | p➝q | ¬q | ((p➝q)∧(¬q)) | ¬p | ((p➝q)∧(¬q))➝(¬p) |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | T |
| T | F | F | T | F | F | T |
| F | T | T | F | F | T | T |
| F | F | T | T | T | T | T |
最后一列全T，所以它是有效推理形式
再比如
推理形式：p➝q, ¬p -> ¬q，复合命题形式：((p➝q)∧(¬p))➝(¬q)
| p | q | p➝q | ¬p | ((p➝q)∧(¬p)) | ¬q | ((p➝q)∧(¬p))➝(¬q) |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | T |
| T | F | F | F | F | T | T |
| F | T | T | T | T | F | F |
| F | F | T | T | T | T | T |
最后一列有一F（反例），所以它不是有效推理形式
真值表法:
- 列出某一命题形式中命题变元的全部真值或真值组合;
- 根据命题变元的真值和相关命题联结词的性质，逐步写出在命题变元的各种真值或真值组合下该命题形式的真值;
- 若某一命题形式在命题变元的全部真值或真值组合下其真值均为真，则证明该命题形式为重言式。
有效推理形式所对应的复合命题形式当且仅当是重言式。
判定重言式的真值表法是能行的方法，即:用机械的方法，在有限的步骤内，一定可以得到结果。
4.5 有效推理形式的判定：归谬赋值法
如果初始命题变元个数过多，会造成真值表行数过多。譬如，有10个初始命题变元，则真值表有2^10=1024行。于是，尝试寻找更简便判定方法。
反证
例如，((p➝q)∧(¬p))➝(¬q) 为 F（假设((p➝q)∧(¬p))➝(¬q)不是重言式）
则(p➝q)∧(¬p)为T，¬q为F
则(p➝q)为T，(¬p)为T，q为T
则p为F，q为T, 符合(p➝q)为T
故((p➝q)∧(¬p))➝(¬q)不是有效的推理形式。
例如，((p➝q)∧(¬q))➝(¬p) 为 F（假设((p➝q)∧(¬q))➝(¬p)不是重言式）
则(p➝q)∧(¬q)为T，¬p为F
则a. (p➝q)为T，b. q为F, p为T
若b. q为F, p为T，则(p➝q)为F，与a. (p➝q)为T矛盾
所以((p➝q)∧(¬q))➝(¬p)不能不是重言式
归谬赋值法:
- 假设某一命题形式不是重言式，即:该命题形式的命题变元，至少存在一种真值或真值组合，使得该命题形式的真值为假;
- 基于上述假设，对该命题形式赋值以假;
- 根据命题联结词的性质，寻找使得上述赋值成立的命题变元真值或真值组合。若能找到(即不出现矛盾)，则上述假设成立，即该命题形式不是重言式;若不可能找到(即不能不出现矛盾)，则上述假设不成立，从而证明该命题形式是重言式。
例如，((p➝q)∧(q➝r)∧(r➝s))➝((¬s)➝(¬p))为F（假设((p➝q)∧(q➝r)∧(r➝s))➝((¬s)➝(¬p))不是重言式）
（日常例子（小孩一考试就紧张，一紧张就考砸，一考砸就被双亲混合双打 -> 小孩没挨打，最近没考试））
则(p➝q)∧(q➝r)∧(r➝s)为T，(¬s)➝(¬p)为F
则p➝q为T，q➝r为T，a. r➝s为T，b. s为F，p为T
则q为T，r为T，s为T，与b互相矛盾
故((p➝q)∧(q➝r)∧(r➝s))➝((¬s)➝(¬p))是重言式（有效推理形式）
归谬赋值法的局限
例如，(p∨q)➝(p∧q)为F（假设(p∨q)➝(p∧q)不是重言式）
则p∨q为T（有三种情况），p∧q为F（有三种情况）
假设p为T，q为F
假设p为F，q为T
解决：用回真值表法
小技巧：变元数量较少，用真值表法；变元数量较多，用归谬赋值法。
有效推理形式的判定:
- 用逻辑符号把具体推理中的前提和结论分别写成命题形式，从而形成推理形式;
- 用蕴涵、合取符号及括号把推理形式转换为复合命题形式;
- 用真值表法或归谬赋值法判定该复合命题形式是否为重言式。
从归谬赋值法看逻辑学的基本准则（同一律，矛盾律，排中律）（逻辑学中不言而喻，显然的基本准则）：
假设p➝p为F
则前p为T，后p为F，这违反同一律，矛盾律。
证明它不能不是重言式，也就是它是重言式，也就是排中律天线（非重言式和重言式没有中间状态度）
第5讲 复合命题的推理：命题联结词的充足集
5.1 命题联结词：真值函数
函数是一种映射
每个命题联结词相当于从真值集合{T,F}到自身{T,F}的一个函数，称为真值函数。
- 每个复合命题形式可以看作一个真值函数。其函数值由其所包含的基本命题(命题变元)的真值、其包含的命题联结词的性质决定。
- 每个复合命题形式对应一个真值函数。
- 不同的命题形式可以对应相同的真值函数。
运用真值表，可以确定任一复合命题形式所对应的真值函数(即，可知在命题变元的各种真值组合下该真值函数的值)。
与此相对，如何为确定的真值函数找出相对应的命题形式?（下一节有解答）
命题联结词¬、∨、∧分别与同数字电路中的非门，与门，或门对应。
5.2 析取范式
一场比赛上，三个裁判有两个及以上通过，才算真正的通过
| P1 | P2 | P3 | f |
|---|---|---|---|
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F | F |
| F | T | T | T |
| F | T | F | F |
| F | F | T | F |
| F | F | F | F |
真正通过的情况：(P1∧P2∧P3) ∨ (P1∧P2∧(¬P3)) ∨ (P1∧(¬P2)∧P3) ∨ ((¬P1)∧P2∧P3)
基本合取式: n个(n=1, 2, 3, …)命题变元或其否定用合取(∧)联结而成的命题形式；
析取范式: n个(n=1，2，3，…)有相同命题变元的基本合取式用析取(∨)联接而成的命题形式。
对应于某个真值函数的析取范式的作法:
- 列出该真值函数的真值表;
- 对于使得该真值函数为真的命题变元各种真值组合:
- 若命题变元的真值为真，则取命题变元本身，
- 若命题变元的真值为假，则取命题变元之否定，
- 再用合取将其联接，构成基本合取式;
- 用析取将各基本合取式联结，构成析取范式。
如何为确定的真值函数找出相对应的命题形式?（回答上一节问题）
运用真值表，列出相应的范式。
范式(normal form)：满足某种规范、能显示某种逻辑性质的命题形式。
5.3 为复合命题形式作与之等值的析取范式
除了个别特殊情况，对于复合命题形式，都可以作出与之等值的析取范式。
p⟷q 与 (p∧q)∨((¬p)∧(¬q)) 等值，用真值表验证。
| p | q | p⟷q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
| p | q | p∧q | ¬p | ¬q | (¬p)∧(¬q) | (p∧q)∨((¬p)∧(¬q)) |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | T |
| T | F | F | F | T | F | F |
| F | T | F | T | F | F | F |
| F | F | F | T | T | T | T |
例如，¬(p➝q)与p∧(¬q)（p∧(¬q)也是析取范式）
| p | q | p➝q | ¬(p➝q) |
|---|---|---|---|
| T | T | T | F |
| T | F | F | T |
| F | T | T | F |
| F | F | T | F |
| p | q | ¬q | p∧(¬q) |
|---|---|---|---|
| T | T | F | F |
| T | F | T | T |
| F | T | F | F |
| F | F | T | F |
例如，¬(((p➝q)∧p)➝q)
| p | q | p➝q | (p➝q)∧p | ((p➝q)∧p)➝q | ¬(((p➝q)∧p)➝q) |
|---|---|---|---|---|---|
| T | T | T | T | T | F |
| T | F | F | F | T | F |
| F | T | T | F | T | F |
| F | F | T | F | T | F |
除矛盾式以外，对于复合命题形式，都可以作出与之等值的析取范式。
为什么矛盾式不行？请回顾对应于某个真值函数的析取范式的作法:
- 列出该真值函数的真值表;
- 对于使得该真值函数为真的命题变元各种真值组合:
…
由于矛盾式总是假，于是在上述的第2步该真值函数为真的命题变元为0，所以矛盾式不能作出析取范式。
5.4 合取范式
基本析取式：n个( n=1，2，3，…)命题变元或其否定用析取(∨)联结而成的命题形式;
合取范式：n个(n=1, 2, 3，…)有相同命题变元的基本析取式用合取(∧)联接而成的命题形式。
对应于某个真值函数的合取范式的作法：
- 列出该真值函数的真值表再加以否定;
- 作出该否定的析取范式;
- 对该析取范式作否定，再反复运用德摩根律和双重否定律加以整理，从而得到对应于原真值函数的合取范式。
| p | q | p⟷q | ¬(p⟷q) |
|---|---|---|---|
| T | T | T | F |
| T | F | F | T |
| F | T | F | T |
| F | F | T | F |
得出p⟷q的合取范式
- p⟷q（1. 列出该真值函数的真值表再加以否定）
- ¬(p⟷q)（2. 作出该否定的析取范式;）
- (p∧(¬q))∨((¬p)∧q)（3. 对该析取范式作否定，再反复运用德摩根律和双重否定律加以整理，从而得到对应于原真值函数的合取范式。）
- ¬((p∧(¬q))∨((¬p)∧q))
反复运用德摩根律和双重否定律加以整理
德摩根律：
- ¬(p∧q) ⟷ (¬p)∨(¬q)
- ¬(p∨q) ⟷ (¬p)∧(¬q)
双重否定：
- ¬(¬p) ⟷ p
- p⟷q（1. 列出该真值函数的真值表再加以否定）
- ¬(p⟷q)（2. 作出该否定的析取范式;）
- (p∧(¬q))∨((¬p)∧q)（3. 对该析取范式作否定，）
- ¬((p∧(¬q))∨((¬p)∧q))（再反复运用德摩根律和双重否定律加以整理）
- ¬(p∧(¬q))∧¬((¬p)∧q))
- ((¬p)∨q)∧(p∨(¬q))
然后用真值表进行验证：
| p | q | p⟷q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
| p | q | ¬p | (¬p)∨q | ¬q | p∨(¬q) | ((¬p)∨q)∧(p∨(¬q)) |
|---|---|---|---|---|---|---|
| T | T | F | T | F | T | T |
| T | F | F | F | T | T | F |
| F | T | T | T | F | F | F |
| F | F | T | T | T | T | T |
除重言式以外，对于复合命题形式，都可以作出与之等值的合取范式。
为什么重言式不能作出合取范式？回顾对应于某个真值函数的合取范式的作法：
- 列出该真值函数的真值表再加以否定;
- 作出该否定的析取范式;
…
重言式加以否定成矛盾式，再回顾对应于某个真值函数的析取范式的作法:
- 列出该真值函数的真值表;
- 对于使得该真值函数为真的命题变元各种真值组合:
…
由于矛盾式总是假，于是在上述的第2步该真值函数为真的命题变元为0，所以矛盾式不能作出析取范式。
所以重言式不能作出合取范式。
5.5 范式存在定理
范式(normal form)：满足某种规范、能显示某种逻辑性质的命题形式。
- 基本合取式: n个(n=1, 2, 3, …)命题变元或其否定用合取(∧)联结而成的命题形式;
- 基本析取式: n个(n=1, 2, 3, …)命题变元或其否定用析取(∨)联结而成的命题形式;
- 析取范式: n个(n=1, 2, 3, …)有相同命题变元的基本合取式用析取(∨)联接而成的命题形式;
- 合取范式: n个(n=1, 2, 3,…)有相同命题变元的基本析取式用合取(∧)联接而成的命题形式。
与p⟷q等值的
- 析取范式：(p∧q)∨((¬p)∧(¬q))
- 合取范式：((¬p)∨q)∧(p∨(¬q))
由范式作法可知：
- 除永假式以外的复合命题形式，都可作与之等值的析取范式，
- 除重言式以外的复合命题形式，都可作与之等值的合取范式。
范式存在定理:
- 每一真值函数，都可用范式(析取范式或合取范式)表示;
- 每一复合命题形式，都至少存在一个与其等值的范式(析取范式或合取范式)。
5.6 命题联结词的充足集
存在多少个不同的n元真值函数(命题联结词)?
答：2(2n)个
例如有两个命题变元：
| p | q | 1 | 2 | … | 16 |
|---|---|---|---|---|---|
| T | T | T | F | … | F |
| T | F | T | T | … | F |
| F | T | T | T | … | F |
| F | F | T | T | … | F |
命题联结词的充足(adequate)集：若干个命题联结词的集合，用这些命题联结词(同命题变元一起)经过有限次的重复和组合，可表示任意的真值函数。
根据范式存在定理，{¬, ∧, ∨}是命题联结词的充足集。
更进一步精简
- (¬((¬A)∧(¬B)))与(A∨B)等值，
- (¬((¬A)∨(¬B)))与(A∧B)等值，
因此，{¬, ∧}和{¬, ∨}也是命题连接词充足集。
再如，
- ((¬A)➝B)))与(A∨B)等值，
- (¬(A➝(¬B)))与(A∧B)等值，
因此，{¬, ➝}也是命题连接词充足集。
小结
{¬, ∧, ∨}是命题联结词的充足集
{¬, ∧}, {¬, ∨}, {¬, ➝}也分别是命题连接词充足集
5.7 命题联结词的独元充足集
一进制理论上可行，但它不实用，不能表示0
或非(nor) ↓
真值表：
| p | q | p↓q |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
| A | A↓A | ¬A |
|---|---|---|
| T | F | F |
| F | T | F |
| A | B | A↓A | B↓B | (A↓A)↓(B↓B) | A∧B |
|---|---|---|---|---|---|
| T | T | F | F | T | T |
| T | F | F | T | F | F |
| F | T | T | F | F | F |
| F | F | T | T | F | F |
| A | B | A↓B | (A↓B)↓(A↓B) | A∨B |
|---|---|---|---|---|
| T | T | F | T | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | T | F | F |
已证{¬, ∧, ∨}是命题联结词的充足集
- (A↓A)与(¬A)等值
- ((A↓A)↓(B↓B))与(A∧B)等值
- ((A↓B)↓(A↓B))与(A∨B)等值
因此，{↓}是命题联结词的充足集。这是很奇妙的结果。
与非与或非也能独当一面
与非(nand) |
真值表：
| p | q | p|q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
- (A|A)与(¬A)等值
- ((A|B)|(A|B))与(A∧B)等值
- ((A|A)|(B|B))与(A∨B)等值
真值表检验过程略
已证{¬, ∧, ∨}是命题联结词的充足集
- (A|A)与(¬A)等值
- ((A|B)|(A|B))与(A∧B)等值
- ((A|A)|(B|B))与(A∨B)等值
因此，{|}是命题联结词的充足集。这是很奇妙的结果。
↓和|称为谢弗尔竖( Sheffer stroke或Shefferbar)。
{↓}和{|}是命题联结词的单元素(独元)充足集。（这是一个非常奇妙的结果）
↓，|对应于数字电路中的或非门，与非门。
第6讲 命题演算：公理系统
6.1 公理系统的构成
判定有效推理形式的方法：真值表法、归谬赋值法。
生成有效推理形式的方法：公理系统、自然推演系统。
公理系统的构成：（数学，物理，逻辑等都有自己公理系统。）
- 符号库(初始符号)
- 形成规则(符号的使用)
- 公理 (推演的起点)
- 变形规则(推演规则)
自然语言的歧义性、模糊性，不能使用在公理系统
例如：这里展示的是三个学生的作品。（有两种解释，应避免歧义的发生）
又例如：《围城》中的老科学家
更精准的人工语言：数学，计算机编程语言
语言的三要素：语音、词汇、语法（盲文，计算机编程语言没有语音）
例子说明公理系统的构成：
- 符号库(初始符号)：如Unicode字符集
- 形成规则(符号的使用)：语法
- 公理 (推演的起点)：2015年4月1日是星期二
- 变形规则(推演规则)：2015年4月7日是星期几？7 - 1 + 1 = 7，(2 + 7 - 1) % 7=1，2015年4月7日是星期一？
6.2 命题演算的公理系统L
更详细公理系统L的信息可查阅A.G.Hamilton的Logic for mathematicians。
命题演算的公理系统L：
- 初始符号：P1, P2, …; ¬, ➝; (,)
- 形成规则：
- P1, P2, …是合式公式;
- 若A，B是任意合式公式，则(¬A),(A➝B)是合式公式;（加括号，防止歧义的发生）
- 所有合式公式由1., 2.生成。
- 公理模式：(设A，B, C是任意合式公式)（都是重言式）
- L1((A➝(B➝A)))
- L2((A➝(B➝C))➝((A➝B)➝(A➝C)))
- L3(((¬A)➝(¬B))➝(B➝A))
- 推演规则：(分离规则，MP)从(A➝B)和A可得B。
合式公式(well-formed formula)(wf.)：合于形成规则的式子(相当于合乎语法的句子)。（这里公式是表达式，不是数学的公式）
6.3 命题演算公理系统L中的证明
L中的证明:
L的合式公式序列，其中每个合式公式满足下列条件之一:
- L的公理，
- 由在先的两个合式公式用MP得出。
这一序列中的最后一个合式公式称为L中的定理。
- L1((A➝(B➝A)))
- L2((A➝(B➝C))➝((A➝B)➝(A➝C)))
- (分离规则，MP)从(A➝B)和A可得B。
例子：
- (P1➝(P2➝P1))…L1
- (P1➝(P2➝P1))➝((P1➝P2)➝(P1➝P1))…L2
- ((P1➝P2)➝(P1➝P1))…MP(2),(1)
这章内容在语形的角度上，而第四章在语意的角度上
例，证(P1➝P1)
- (P1➝((P1➝P1)➝P1))…L1
- ((P1➝((P1➝P1)➝P1))➝((P1➝(P1➝P1))➝(P1➝P1)))…L2
- ((P1➝(P1➝P1))➝(P1➝P1))…MP(1, 2)
- (P1➝(P1➝P1))…L1
- (P1➝P1)…MP(3,4)
上述定理需要更专业知识证明，我们浅尝辄止则可。
6.4 命题演算公理系统L中的证明（续）
例 证((¬P1)➝(P1➝P2))
- ((¬P1)➝((¬P2)➝(¬P1)))…L1
- (((¬P2)➝(¬P1))➝(P1➝P2))…L1
- ((¬P1)➝(P1➝P2))
上述证明无效，因L系统没有蕴涵连锁，所以任何直观、显然的东西，在这里是不允许的。必须按照3条公理模式和一个推演规则来进行。
正确的证明：
证((¬P1)➝(P1➝P2))
- ((¬P1)➝((¬P2)➝(¬P1)))…L1
- (((¬P2)➝(¬P1))➝(P1➝P2))…L3
- ((((¬P2)➝(¬P1))➝(P1➝P2))➝((¬P1)➝(((¬P2)➝(¬P1))➝(P1➝P2)))…L1
- ((¬P1)➝(((¬P2)➝(¬P1))➝(P1➝P2)))…MP 3., 2.
- (((¬P1)➝(((¬P2)➝(¬P1))➝(P1➝P2)))➝(((¬P1)➝((¬P2)➝(¬P1)))➝((¬P1)➝(P1➝P2))))…L2
- (((¬P1)➝((¬P2)➝(¬P1)))➝((¬P1)➝(P1➝P2))))…MP 5., 4.
- ((¬P1)➝(P1➝P2))…MP 6., 1.
6.5 命题演算公理系统L中的推演
L中的推演：
设Γ（伽玛γ的大写）是L中的合式公式（不必是L中的公理）的集合。Γ中的合式公式作为临时公理参与L中的证明，称为L中从Γ的推演，得到的结果A称为L中Γ的推论。
记为Γ┝(下标L符)A
例子：
- (P1➝P2)…Γ1
- ((P1➝P2)➝(P1➝(P1➝P2)))…L1
- (P1➝(P1➝P2))…MP 2., 1.
(P1➝P2)┝(下标L符)(P1➝(P1➝P2))
例
假设:
- 物体若不受外力，则运动方向 不变;
- 某天体运动方向发生了变化。
- P1：某物受到外力;
- P2：某物运动方向发生变化。
- ((¬P1)➝(¬P2))…Γ1
- P2…Γ2
- (((¬P1)➝(¬P2))➝(P2➝P1))…L3
- (P2➝P1)…MP 3., 1.
- P1…MP 4., 2.
{((¬P1)➝(¬P2)), P2} ┝(下标L符) P1
L中的定理A可记为∅┝(下标L)A，或┝(下标L)A（逻辑内的东西）
第7讲 命题演算：公理系统，自然演绎系统
7.1 公理系统出发点的延伸
公理系统的构成：
- 符号库(初始符号)
- 形成规则(符号的使用)
- 公理 (推演的起点)
- 变形规则(推演规则)
命题演算的公理系统L：
- 初始符号：P1, P2, …; ¬, ➝; (,)
- 形成规则：
- P1, P2, …是合式公式;
- 若A，B是任意合式公式，则(¬A),(A➝B)是合式公式;（加括号，防止歧义的发生）
- 所有合式公式由1., 2.生成。
- 公理模式：(设A，B, C是任意合式公式)（都是重言式）
- L1((A➝(B➝A)))
- L2((A➝(B➝C))➝((A➝B)➝(A➝C)))
- L3(((¬A)➝(¬B))➝(B➝A))
- 推演规则：(分离规则，MP)从(A➝B)和A可得B。
延伸：
1.可用定义引入其他符号。可用初始符号定义其他符号及其形成规则
如：(设A, B, C是任意合式公式，下同)
- (A∨B)定义为((¬A)➝B)
- (A∧B)定义为(¬(A➝(¬B)))
已由定义引入的符号可用于定义更多符号。
由定义引入的新符号可与初始符号同等使用。
2.已证定理可与公理同等使用
如：
已证定理（模式）(A➝A)编为T1，则可有如下证明：（T，Theory缩写）
证 (P1➝P1)
- (P1➝P1)…T1（证毕）
3.已证新的推演规则可与原有推演规则同等使用
如：已证：(A➝B)和(B➝C)可得(A➝C)(假言三段论，HS),（这定理的证明过程可查阅A.G.Hamilton的Logic for mathematicians）
则可有以下证明：
证((¬P1)➝(P1➝P2))
- ((¬P1)➝((¬P2)➝(¬P1)))…L1
- (((¬P2)➝(¬P1))➝(P1➝P2))…L3
- ((¬P1)➝(P1➝P2))…HS 1., 2.
公理系统出发点的延伸:
- 可用定义引入其他符号及其形成规则;
- 已证定理可与公理同等使用;
- 已证新的推演规则可与原有推演规则同等使用。
7.2 公理系统的评价
-
真值表法、归谬赋值法：判定有效推理形式的方法;
-
公理化方法：生成有效推理形式的方法。
-
真值表方法，“重言式”：语义的概念;（有关真假）
-
公理化方法，“定理”：语形的概念。（无关真假）
L系统的性质
- 可靠性：L的定理都是重言式
- 完全性：对应于复合命题有效推理形式的重言式都是L的定理
- 独立性：L的各条公理不能互相推出
L系统的可靠性和完全性使得：L的定理当且仅当是第四讲中的重言式，
即:
L的定理集与第四讲中的重言式集完全相同。
公理系统例子：
- L : L1, L2, L3 （可靠，完全，独立）
- L’ : L1, L2 （可靠，不完全，独立）
- L" : L1, L2, L3, L4(A➝A)（L4多余的，但在运用时更加方便）（可靠，完全，不独立）
L系统为什么要用这个3条公理模式和那个分离规则来作为它的出发点？
答：因为这几条，它可以用最简洁的方法，最大限度地覆盖所有的这个定理。你靠这个三条公理模式，加上那个分离规则，它刚好把所有定理都覆盖了，而且并没有超出它的范围，没有把这个非重言式也拿进来，就是它的定理刚好，正好是重言式，不比重言式少，也不比重言式多，而且它本身的公理还互相独立，它还一条都不多余。三条公理模式，加上那个分离规则构造成一个巧妙的系统。
7.3 公理系统的性质和评价及其意义
公理系统能运用在数学、物理、逻辑等成熟的学科上。
公理系统在文科作整理尝试：
- 斯宾诺莎(1632-1677)：《用几何学方法作论证的伦理学》
凡是想在学识方面超群绝伦的人都一致认为:在研究和传授学问时，数学方法，即从定义、公设和公理推出结论的方法，乃是发现和传授真理最好的和最可靠的方法。这是千真万确的。————路德维希●梅耶尔:斯宾诺莎《笛卡儿哲学原理(依几何学方式证明)》序(1663年)
公理：各个数学分支都通用的一些最基本的东西，如等量代换
公设：用于某一门具体的数学分支一些最基本的东西
对于日常生活参照的意义：
- 法律千万条，大部分都不能全被知道，但我们没有轻易触犯它们，因为我们知道基本的出发点，如，不能损人利己，若损，轻则违道，重则违法。“不能损人利己”相当于公理。
- 勤洗手，不吃脏东西…讲卫生（公理）。
- 好学生如何定义，成绩好，品德好…德智体美劳（公理）。
- 清华大学校训：自强不息（对自己），厚德载物（对外界）。
- 北京精神：爱国，创新，包容，厚德。
7.4 命题演算的自然演绎系统
公理系统的弱点：不够直观。自然演绎系统应运而生。
通过自然演绎系统进行证明和推演的步骤:
- 引入假设;
- 使用给定的接近于日常思维的推演规则进行推演;
- 最后若按照规则消去假设，则得到不依赖于假设的一般定理；若保留假设，则得到依赖于假设之下的推论。
命题演算的自然演绎系统C
- 初始符号：P1, P2, …; ¬, ➝; (,)
- 形成规则：
- P1, P2, …是合式公式;
- 若A，B是任意合式公式，则(¬A),(A➝B)是合式公式;（加括号，防止歧义的发生）
- 所有合式公式由1., 2.生成。
- 推演规则：（设A, B是任意合式公式）
- 假设引入
- 重述
- 重复
- ➝引入
- ¬消去
（如，归谬赋值法） - ➝消去
（如公理系统的分离规则）
- 假设引入
上面1. 2. 与公理系统L的一致
7.5 命题演算自然演绎系统中的证明和推演
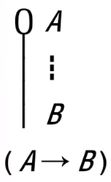
例 证(P1➝P1)
例 证((¬P1)➝(P1➝P2))
例 证(P1➝(P2➝P1))
例 证((P1➝(P2➝P3))➝((P1➝P2)➝(P1➝P3)))
例 证(((¬P1)➝(¬P2))➝(P2➝P1))
通过自然演绎系统进行证明和推演的步骤:
- 引入假设;
- 使用给定的接近于日常思维的推演规则进行推演;
- 最后若按照规则消去假设，则得到不依赖于假设的一般定理；若保留假设，则得到依赖于假设之下的推论。
命题演算的自然演绎系统C具有可靠性、完全性。
命题演算的自然演绎系统C与命题演算的公理系统L等价。即：二者的定理集完全相同。
第8讲 基本命题的构成
8.1 基本命题的结构
基本命题的组成部分：
- 谓词§
- 主词(S)
- 量词
| 量词 | 主词 | 谓词 |
|---|---|---|
| 所有 | 金属 | 是导体 |
| 有的 | 人 | 会游泳 |
主词和谓词都是词项。
- 词项：事物、事物的情况(性质或关系)。
- 命题：对事物及其情况(性质、关系)的陈述。
8.2 词项的内涵和外延
内涵：某一词项的含义，即该词项所指对象共同具有的特有属性。（什么是金属？具有导电，导热等性质的物质）
外延：某一词项所指的对象。（金属的外延是金银铜铁等）
内涵和外延之间有反变关系。
词项的限制：增加词项的内涵以缩小外延;
词项的扩大：减少词项的内涵以扩大外延。
例如，学校的外延：小学，中学，大学等。
学校的内涵：专门进行教育的机构
现在为学校加点内涵：专门进行高等教育的机构。
学校的外延缩小至：大学
8.3 词项的种类
根据词项外延的数量情况，词项分为
- 普遍词项：外延超过一个
- 单独词项：外延只有一个;
- 空词项：外延为空。（美国女总统，数学纯黄金）
8.4 词项间的关系
词项间的关系：指词项外延之间的关系。
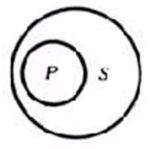
欧拉图解
1.全同（同一）关系
如，本学期选修逻辑学的50名学生，与今天逻辑学课上现场50名学生。（不管内涵是否一样）
如，中国的首都，与华北最大的城市。（内涵不一样，但外延指的是北京）
如，中国最大的城市，长江流域最大的城市。（内涵不一样，但外延指的是上海）
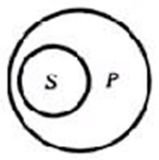
2.包含关系
如，S:中国的学校，P:中国的大学
3.包含于关系
如，S:中国的大学，P:中国的学校
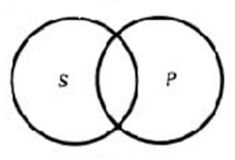
4.交叉关系
如，S：北京人，P：学生。
5.全异关系
如，S：幼儿园学生，P：大学生
- 矛盾关系（互补的，例如，学校男女生）
- 反对关系（不互补，大学生和小学生，因为还有中学生得等，这里的“反对”与日常的“反对”不同）
小结：
词项间的关系：
- 全同(同一)关系
- 包含关系
- 包含于关系
- 交叉关系
- 全异关系:
- 矛盾关系
- 反对关系
8.5 词项的定义
定义：描述词项的内涵
定义的结构：被定义项，定义项
偶数 是能被2整除的数。
（被定义项）（定义项）
同一个词项可有不同的定义
- 水是无色无味的、在一个大气压下冰点为0摄氏度沸点为100摄氏度的、比重为1的透明液体。
- 水是由两个氢原子和一个氧原子化合成一个水分子而构成的物质。
定义的主要规则：
- 定义项和被定义项须为全同关系。
- 如，鱼是生活在水中的动物。(定义过宽)
- 如，期刊是每周或每月定期出版的出版物。（定义过窄)
- 定义项不得直接或间接包含被定义项。
- 如，逻辑学是研究逻辑的学问。(同语反复)
- 如，偶数是奇数加1或减1得到的数;奇数是偶数加1或减1得到的数。(循环定义)
定义不是唯一获得知识的来源，（有靠实践得来的，如太阳，月亮等）
8.6 词项的划分
划分：分类列举词项的外延。
划分的结构：母项，子项。
生物分为动物、植物、微生物、
（母项）（子项）
句子分为陈述句，疑问句，祈使句，感叹句。
（母项）（子项）
句子分为主语、谓语、宾语、补语、定语。（这不是划分，而是组成部分）
同一个词项可按不同标准作不同的划分。
划分可连续进行，即：子项可作为母项再次进行划分。（学校分为大学，中学，小学。大学划分为中国大学、美国大学等）
划分的主要规则：
- 一次划分必须按同一标准进行。
- 每一外延应属于某一子项并只属于一个子项。即:
- 子项相加应恰等于母项，不得遗漏;
- 子项之间应互相排斥不得重合。
8.7 谓词的分类
谓词是什么东西什么样，说明事物情况，说明一种性质，说明一种关系。
- 张三和李四是高中学生。（复合命题，张三是高中学生并且李四是高中学生）
- 张三和李四是同班同学。（你不能说成张三是同班同学并且李四是同班同学）
一元谓词：每次需要一个主词与之配合，通常表示主词的某种性质;
多元（如二元，三元，…）谓词：每次需要多个（如两个，三个，…）主词与之配合，通常表示多个主词之间的某种关系。
- 性质命题：含有一元谓词的基本命题;
- 关系命题：含有多元谓词的基本命题。
三元的例子：福州在广州与上海之间。
8.8 量词
例子：
- 所有金属导电。
- 有些人会游泳。
“所有”，“有些”为量词，限定外延
量词：
- 全称（∀）(all)
- 特称（存在）（∃）(existed)
- 单称
特称(存在)量词的含义：至少存在一个(不排斥全部)。
单称量词通常处理为全称。（独一无二的为单称，如北京大学）
全称量词可省略。（如，金属是导体。特称量词不能省略，“有些人会游泳”省略成“人会游泳”）。
8.9 联词
传统逻辑中，往往把“否定”分析为在性质命题内部与“肯定”相对的成分。
“肯定”和“否定”称为联词，表明主词和谓词之间具有肯定的联系或否定的联系。
- 今天是星期四
- 今天不是星期四
小结：
基本命题的组成部分：
- 谓词
- 主词
- 量词
- （联词）
第9讲 传统逻辑中基本命题的推理
9.1 基本命题的推理
复合命题的推理：以复合命题为前提或结论，以命题联接词的性质为推理依据。
基本命题的推理：以基本命题为前提和结论，以基本命题的内部成分和结构为推理依据。
基本命题：本身不再包含其他命题的命题。
复合命题：由一个或多个基本命题加上命题联结词所构成的命题。
9.2 传统逻辑对基本命题的分析
传统逻辑对性质命题的分析
- 主词(S)
- 谓词§
- 量词：全称，特称，单称
- 联词：肯定，否定
根据量词(全称、特称)、联词(肯定、否定)的组合
性质命题分为:
- 全称肯定(SAP)：所有S是P (A)
- 全称否定(SEP)：所有S不是P (E)
- 特称肯定(SIP)：有S是P (I)
- 特称否定(SOP) :有S不是P (O)
AEIO源于拉丁字母，请记住其含义。
9.3 性质命题中主、谓词的周延
周延：词项作为主词、谓词出现在性质命题中时，是否涉及到其全部外延，称为是否周延。（下面加下划线为周延）
-
全称肯定(SAP) : (所有S是P)（例，所有金属都是导体）
-
全称否定(SEP) : (所有S不是P)（例，所有金属都不是绝缘体）
-
特称肯定(SIP) : (有S是P)（例，有的北京人是大学生）
-
特称否定(SOP) : (有S不是P)（例，有的人不是大学生）
-
全称命题(A、E)的主词周延
-
特称命题(I、O)的主词不周延
-
否定命题(E、O)的谓词周延
-
肯定命题(A、I)的谓问不周延
关于词项周延的一般规则:
推理中，在前提中出现时不周延的词项，在结论中出现时也不得周延。
9.4 命题变形的推理
1.换位法：
- SEP可推出PES（例，所有金属都不是绝缘体 推出 所有绝缘体都不是金属）
- SIP可推出PIS（例，有的大学生是北京人 推出 有的北京人为大学生）
- SAP可推出PIS（例，所有金属都是导体 推出 有的导体是金属）
关于词项周延的一般规则:
推理中，在前提中出现时不周延的词项，在结论中出现时也不得周延。
错例：
- SAP, PAS（例，所有金属都是导体，所有导体都是金属 X，有的导体是金属）
- SOP, POS（例，有的鸟不是动物，有的动物不是鸟）（貌似说得过去）
2.换质法：
- SAP可推出SEP（例，所有金属都是导体，推出 所有金属都不是非导体）
- SEP可推出SAP（例，所有金属都不是绝缘体，推出 所有金属都是非绝缘体）
- SIP可推出SOP（例，有的北京人是学生，推出 有的北京人不是非学生）
- SOP可推出SIP
9.5 根据对当关系的推理
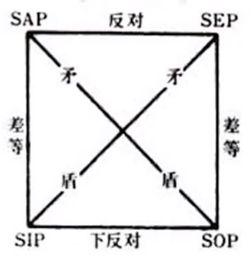
逻辑方阵
-
反对：可以同假，不能同真（例，SAP-所有金属都是导体，SEP所有金属都不是导体）
-
下反对：可以同真，不能同假（例，SIP-有的人会游泳，SOP-有的人不会游泳）
-
矛盾：必一真一假（例，SEP-所有金属都不是导体，SIP-有的金属是导体）
-
差等：上真下必真，下假上必假（例，SAP-所有金属都是导体（上真），SIP-有的金属是导体（下必真））（例，SAP-所有的人都会游泳（假），SIP-有的人会游泳（真））
-
SAP可推出¬(SEP), SIP,¬(SOP)
-
¬(SAP)可推出SOP
-
SEP可推出¬(SAP),¬(SIP),SOP
-
¬(SEP)可推出SIP
-
SIP可推出¬(SEP)
-
¬(SIP)可推出¬(SAP), SEP, SOP
-
SOP可推出¬(SAP)
-
¬(SOP)可推出SAP,¬(SEP), SIP
9.6 三段论
三段论:
由包含一个共同词项的两个性质命题作为前提，推出一个性质命题作为结论的推理形式。
- （所有金属是导体，所有钢铁是金属） -> 所有有钢铁是导体
- （所有金属是导体，有的塑料不是导体） -> 有的塑料不是金属
三段论的结构:
（先看结论）作为结论之主词的词项称为小词(S)，作为结论之谓词的词项称为大词§，（再到前提）只出现在前提中的词项称为中词(M)。
含有大词的前提称为大前提，含有小词的前提称为小前提。
9.7 三段论的式与格
式：由作为大前提、小前提、结论的性质命题的种类而确定。
- （所有金属是导体MAP，所有钢铁是金属SAM） -> 所有有钢铁是导体SAP AAA式
- （所有金属是导体，有的塑料不是导体） -> 有的塑料不是金属 AOO式
AAA…OOO，共4 * 4 * 4 = 64种
- (所有金属是导体MAP, 所有钢铁是金属SAM) -> 所有铜铁是导体SAP
- (所有金属是导体PAM, 所有钢铁是导体SAM) -> 所有钢铁是金属SAP
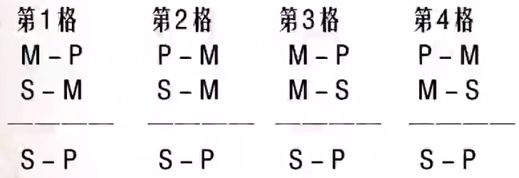
格：由中词、大词、小词在前提中的位置而确定。
共有4个格：
- (所有金属是导体MAP, 所有钢铁是金属SAM) -> 所有铜铁是导体SAP AAA-1
- (所有金属是导体PAM,有的塑料不是导体SOM) -> 有的塑料不是金属SOP AOO-2
- 式：由作为大前提、小前提、结论的性质命题的种类而确定，共有64个不同的式
- 格：由中词、大词、小词在前提中的位置而确定，共有4个格
- 三段论结合式与格，共有256种可能的格式
9.8 有效三段论的判定
1.写成三段论的标准形式。
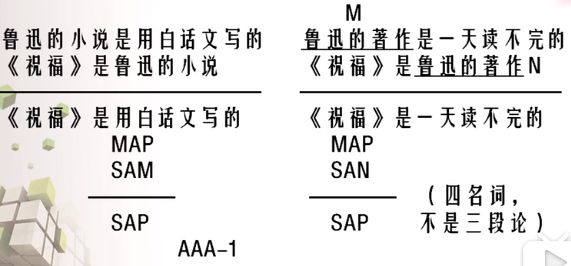（鲁迅著作前后不一，上一句表示鲁迅全部著作，下一句为鲁迅一本著作）
2.若结论为肯定命题，则两个前提必定均为肯定命题；若结论为否定命题，则两个前提必定一为肯定命题、一为否定命题。
3.中词在前提中至少周延一次（中词是用来作媒介）
周延：词项作为主词、谓词出现在性质命题中时，是否涉及到其全部外延，称为是否周延。
4.小词、大词在结论中若周延，则其在前提中必须周延。
有效三段论的判定四条方法
- 写成三段论的标准形式;
- 若结论为肯定命题，则两个前提必定均为肯定命题;若结论为否定命题，则两个前提必定一为肯定命题、一为否定命题。
- 中词在前提中至少周延一次。
- 小词、大词在结论中若周延，则其在前提中必须周延。
三段论有效格式的特征
三段论的有效格式
弱称（上图带括号的）：本来可以得到全称的，但是你现在给出是特称，它的有效性是由条件的。
不推荐背诵这三段论的有效格式，但推荐背诵有效三段论的判定四条方法
第10讲 基本命题的推理
10.1 性质命题
基本命题的组成部分:
- 谓词
- 主词
- 量词
一元谓词：每次需要一个主词与之配合，通常表示主词的某种性质；
多元(如二元，三元，…)谓词：每次需要多个(如两个，三个，…)主词与之配合，通常表示多个主词之间的某种关系。
性质命题：含有一元谓词的基本命题；
关系命题：含有多元谓词的基本命题。
-
P: 谓词变元
-
x: 个体变元
-
P(x): x是P (x有性质P)
-
量词:∀，∃
-
(∀x)(P(x)): 所有x是P
-
(∃x)(P(x)): 至少存在一个x是P
量词∀和∃之间可以互相替换表达：
- (∀x)(P(x))与¬(∃x)(¬P(x))等值
- (∃x)(P(x))与¬(∀x)(¬P(x))等值
性质命题在数理逻辑中的表述
- 全称肯定(SAP)(所有S是P) : (∀x)(S(X)→P(x))
- 全称否定(SEP)(所有S不是P) : (∀x)(S(x)→(¬P(x)))
- 特称肯定(SIP)(有S是P) : (∃x)(S(x)∧P(x))
- 特称否定(SOP)(有S不是P) : (∃x)(S(x)∧¬P(x))
SAP与SOP，SEP与SIP的矛盾关系
- (∀x)(S(X)→P(x))与¬(∃x)(S(x)∧¬P(x))与同值
- (∀x)(S(x)→(¬P(x)))与¬(∃x)(S(x)∧P(x))同值
- (∃x)(S(x)∧P(x))与¬(∀x)(S(X)→¬P(x))同值
- (∃x)(S(x)∧¬P(x))与¬(∀x)(S(x)→(P(x)))同值
10.2 主词非空的预设
预设：预先的假设（说话人和听话人不言自明的东西）
- 你什么时候回来？（预设：你将要离开。）
- 你戒烟了吗？（预设：你曾经抽烟。对非抽烟者，该问题不成立。）
全称命题推出存在命题时，须预设：前提中主词(S)不为空词项。
若前提中主词为空词项，则从全称命题到存在命题的推理不成立。
空词项：外延为空。（美国女总统，数学纯黄金）
例，美国外交官说“我不能竞选美国总统。”，在美国出生的人才有资格竞选总统，且他不是出生在美国。
不能直接从(∀x)(S(x)→P(x))（即A命题），推出(∃x)(S(x)∧P(x))（即I命题）
例，S(x)：这人是美国女总统，P(X)：这人是在美国出生的。
若从A命题推出I命题，须增加前提(∃x)(S(x))，即从(∀x)(S(X)→P(x))∧(∃x)(S(x))，推出(∃x)(S(x)∧P(x))
例。对于上例，(∃x)(S(x))：至少有一个美国女总统。
上图中5个带括号的格式，在传统逻辑是可以的，但在严格地说，它们有条件。
三段论中，若小词为空词项，那么弱式将不成立。
10.3 关系命题的结构
关系命题：含有多元谓词的基本命题，如二元关系命题：
R(x, y)：x对于y，有关系R
R：谓词变元
x, y：个体变元
量词：∀，∃
-
(∀x)(∀y)R(x, y)
-
(∀y)(∀x)R(x, y)
-
(∀x)(∃y)R(x, y)
-
(∃y)(∀x)R(x, y)
-
(∃x)(∀y)R(x, y)
-
(∀y)(∃x)R(x, y)
-
(∃x)(∃y)R(x, y)
-
(∃y)(∃x)R(x, y)
例如：
R：害怕
x：老鼠
y：猫
10.4 关系命题根据量词的推理
(∀x)(∀y)R(x, y) ⇔ (∀y)(∀x)R(x, y)
⇓
(∀x)(∃y)R(x, y) ⇐ (∃y)(∀x)R(x, y)
(∃x)(∀y)R(x, y) ⇒ (∀y)(∃x)R(x, y)
⇓
(∃x)(∃y)R(x, y) ⇔ (∃y)(∃x)R(x, y)
10.5 关系命题根据谓词性质的推理方法
1.自返性
- 自反关系：(∀x)R(x, x)（例，数学上的等于）
- 反自返关系：(∀x)(¬R(x, x))（例，数学上的大于）
- 非自返关系：((∃x)R(x, x))∧((∃x)(¬R(x, x)))（例，有的人能正确认识自己，有的人不能正确认识自己）
2.对称性
- 对称关系：(∀x)(∀y)((R(x,y))⇒(R(y,x)))（例，直线a与直线b平行，直线b与直线a平行）
- 反对称关系：(∀x)(∀y)((R(x,y))⇒(¬R(y,x)))（例，张三是李四的哥哥）
- 非对称关系：((∃x)(∃y)((R(x,y))⇒(R(y,x))))∧((∃x)(∃y)((R(x,y))⇒(¬R(y,x))))（例，爱慕关系，存在张三李四互相爱慕，并且张三一厢情愿爱慕李四）
3.传递性
- 传递关系：(∀x)(∀y)(∀z)(((R(x,y)∧R(y,z)))⇒R(x,z))（例，A大于B，B大于C，A大于C）
- 反传递关系：(∀x)(∀y)(∀z)(((R(x,y)∧R(y,z)))⇒(¬R(x,z)))(例，平面上，A垂直于B，B垂直于C，A不垂直于C)
- 非传递关系：((∃x)(∃y)(∃z)(((R(x,y)∧R(y,z)))⇒R(x,z)))∧((∃x)(∃y)(∃z)(((R(x,y)∧R(y,z)))⇒(¬R(x,z))))（例，朋友的朋友）
请注意:
“关系命题根据谓词性质的推理方法”只是给出了一种方法，不是纯形式的逻辑推理。
10.6 谓词演算简介
用于谓词演算的一阶语言
符号库：
合式公式：合于形成规则的式子(相当于合乎语法的句子)。（这里公式是表达式，不是数学的公式）
- 一阶谓词演算
- 高阶谓词演算
- 谓词演算的公理系统
- 谓词演算的自然演绎系统
第11讲 非经典逻辑的初步
11.1 非经典（非标准）逻辑
- 古典逻辑
- 经典逻辑
- 非经典逻辑（经典逻辑的补充）
11.2 多值逻辑
源于亚里士多德
如三值逻辑，命题的真值可取：
- T(真), I(可能), F(假)
- 1, 2, 3
- 0, 1/2, 1
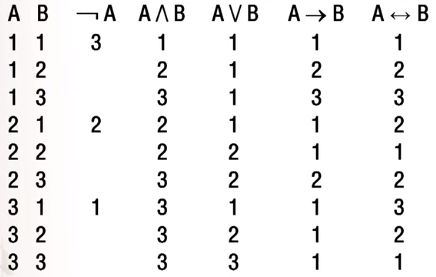
卢卡西维茨(1878-1956)：1920年《论三值逻辑》，首次提出多值逻辑的系统
卢卡西维茨的卢卡西维茨的真值表
11.3 模糊逻辑
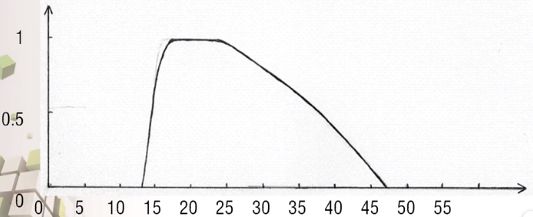
即无穷多连续值逻辑：扎德(1921年生)于1965年提出模糊集合概念
模糊逻辑将模糊的东西变得精确
命题真值取值为“隶属度”，在[0，1]之间连续取值
11.4 模态逻辑
含有必然、可能等模态(modal)词的命题及其推理
亚里士多德的模态三段论
刘易斯( 1883-1964) 于1914年构造模态命题演算系统
基本模态词：
- 必然□
- 或然◇
- □P：必然p
- ◇p：可能p
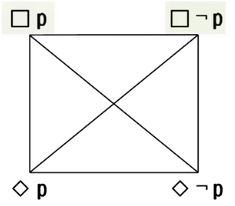
- 反对(不能同真可以同假)：□p与□¬p
- 下反对(不能同假可以同真)：◇p与◇¬p
- 矛盾(必一真一假)：□p与◇¬p，□¬p与◇p
- 差等(上真下必真，下假上必假)：□p对◇p，□¬p对◇¬p
根据模态命题之间的矛盾关系:
- “必然”等值于“不可能不”
- “可能”等值于“不必然不”
- “不可能”等值于“必然不”
- “不必然”等值于“可能不”
不包含模态词的命题可视为模态的特例：实然
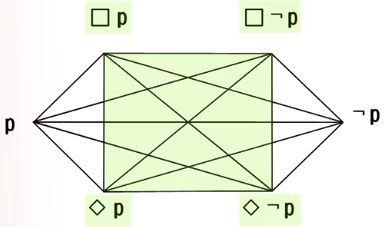
- 反对(不能同真可以同假)：□p与□¬p，□p与¬p，□¬p与p
- 下反对(不能同假可以同真)：◇p与◇¬p，◇p与¬p，◇¬p与p
- 矛盾(必一真一假)：□p与◇¬p，□¬p与◇p，p与¬p
- 差等(上真下必真，下假上必假)：□p对◇p，□¬p对◇¬p，□p对p，p对◇p，□¬p对¬p，¬p对◇¬p
11.5 规范逻辑
含有必须、允许等规范词的规范命题及其推理，亦称道义逻辑、义务逻辑等。
冯、赖特(1916-2003)于1951年发表《规范逻辑》，并创立规范逻辑系统。
基本规范词:
- 必须 O
- 允许 P
- 禁止(必须不) F
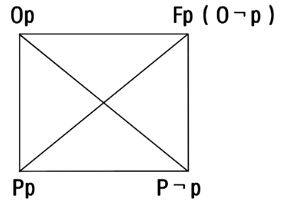
Op:必须p，Pp:允许p，Fp:禁止p
- 反对(不能同真可以同假)：Op与Fp
- 下反对(不能同假可以同真)：Pp与P¬p
- 矛盾(必一真一假)：Op与P p，Fp与Pp
- 差等(上真下必真，下假上必假)：Op对Pp，Fp对P¬p
根据规范命题之间的矛盾关系:
- “必须”等值于“不允许不”
- “允许”等值于“不禁止”
- “允许”等值于“不禁止”
- “不必须”等值于“允许不”
11.6 时态逻辑
含有过去、现在、将来、永远等时态词的时态命题及其推理
亦称时间逻辑、时序逻辑等
普莱尔(1914-)于1957年建立时态逻辑的两个系统
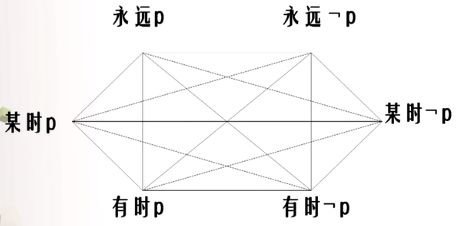
- 反对(不能同真可以同假)：
- 永远p与永远¬p，永远p与某时¬p，永远¬p与某时p
- 下反对(不能同假可以同真)：
- 有时p与有时¬p，有时p与某时¬p，有时¬p与某时p
- 矛盾(必一真一假)：
- 永远p与有时¬p，永远¬ρ与有时p，某时p与某时¬p
- 差等(上真下必真，下假上必假)：
- 永远p对有时p，永远p对某时p，某时p对有时p,
- 永远¬p对有时¬p,永远¬p对某时¬p,某时¬p对有时¬p
时态命题中可引入模态命题，构成时态模态命题，将来可能等
规范逻辑、时态逻辑等都属于广义模态逻辑
11.7 弗协调逻辑
亦称次协调逻辑、超协调逻辑、亚相容逻辑等
雅斯可夫斯基于1940年代末构造第一个次协调逻辑系统
达科斯塔(1929年生)建立更完善的次协调逻辑理论
协调(相容)：不存在合式公式A使得A和(¬A)都是定理。
不足道(平庸)：所有合式公式都是定理。
经典逻辑系统是协调而非不足道的。
若非协调则必定不足道(从相互矛盾的两个前提可以推出一切)。
弗协调：既非协调亦非不足道，即：存在合式公式A使得A和(¬A)都是定理，但并非所有合式公式都是定理。
在弗协调逻辑中：不矛盾律(¬(A∧¬A) )并非普遍有效；从相互矛盾的两个前提不能推出一切。
第12讲 余论
12.1 演绎和归纳
- 传统逻辑
- 演绎:从一般到个别
- 归纳:从个别到一般
- 类比:从个别到个别
- 现代逻辑
- 演绎:必然性推理
- 归纳:或然性推理
完全归纳推理
归纳疑难 又称休谟(1711-1776)问题：
- 归纳的根据是归纳本身?
- 归纳的根据何在?
12.2 探求因果关系的逻辑方法
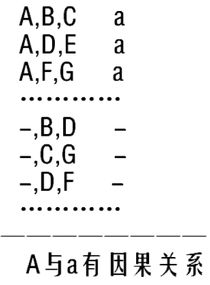
1.求同法（契合法）
2.求异法（差异法）
3.求同求异并用法（契合差异并用法）
4.共变法
5.剩余法
12.3 证论和反驳
论证:
根据已知为真的命题，通过推理确定某一命题的真实性。
- 论题
- 论据
- 论证方式
推理：
- 前提
- 推理形式
- 结论
论证：
- 论据
- 论证方式
- 论题
论据必须是真
间接论证:
- 排除法(剩余法)：A或B或C，非B，非C，从而A。
- 反证法：非A假，从而A真。
反驳：论证某一命题虚假，或确定某一论证不能成立。
归谬法：若A真，则引出矛盾：可见A假。
谬误
- 论题不清
- 虚假论据
- 循环论证
- 诉诸权威
- 以先后为因果
- 转移论题
- 预期理由
- 以人为据
- 诉诸感情
- 以相对为绝对
12.4 悖论
悖论：
由其真可推出其假、由其假可推出其真的命题。
A与其自身的否定非A等值。
说谎者悖论：
“我正在说谎。”“这句话是假的。”
解决：“不自指。”
理发师悖论：
“某村理发师规定给并且只给任何不给自己刮胡子的村民刮胡子。”
解决：“不自指。”
“不能用少于十八个汉字定义的最小整数。”
12.5 本课程《逻辑学概论》内容回顾
- 第1讲 什么是逻辑学？
- 1.1 “逻辑和逻辑学
- 1.2 推理和推理形式
- 1.3 有效推理形式
- 1.4 逻辑学的特点
- 1.5 逻辑学的基本准则
- 1.6 逻辑学和其他学科的关系
- 1.7 关于本课程《逻辑学概论》
- 第2讲 逻辑学的产生与发展
- 2.1 中国古代逻辑思想（上）
- 2.2 中国古代逻辑思想（中）
- 2.3 中国古代逻辑思想（下）
- 2.4 印度古代逻辑
- 2.5 古希腊和中世纪逻辑
- 2.6 近代西方逻辑
- 2.7 数理逻辑的提出和实现
- 2.8 数理逻辑的发展
- 第3讲 命题联结词及其基本推理形式
- 3.1 推理和命题
- 3.2 基本命题和复合命题
- 3.3 常用命题联结词及其基本推理形式（1）
- 3.4 常用命题联结词及其基本推理形式（2）
- 3.5 常用命题联结词及其基本推理形式（3）
- 3.6 常用命题联结词及其基本推理形式（4）
- 3.7 常用命题联结词及其基本推理形式（5）
- 3.8 常用命题联结词及其基本推理形式（6）
- 3.9 常用命题联结词及其基本推理形式（7）
- 第4讲 复合命题的推理：有效推理形式的判定
- 4.1 重言式、矛盾式和可满足式
- 4.2 具体推理转换为推理形式
- 4.3 推理形式转换为复合命题形式
- 4.4 有效推理形式的判定：真值表法
- 4.5 有效推理形式的判定：归谬赋值法
- 第5讲 复合命题的推理：命题联结词的充足集
- 5.1 命题联结词：真值函数
- 5.2 析取范式
- 5.3 为复合命题形式作与之等值的析取范式
- 5.4 合取范式
- 5.5 范式存在定理
- 5.6 命题联结词的充足集
- 5.7 命题联结词的独元充足集
- 第6讲 命题演算：公理系统
- 6.1 公理系统的构成
- 6.2 命题演算的公理系统L
- 6.3 命题演算公理系统L中的证明
- 6.4 命题演算公理系统L中的证明（续）
- 6.5 命题演算公理系统L中的推演
- 第7讲 命题演算：公理系统，自然演绎系统
- 7.1 公理系统出发点的延伸
- 7.2 公理系统的评价
- 7.3 公理系统的性质和评价及其意义
- 7.4 命题演算的自然演绎系统
- 7.5 命题演算自然演绎系统中的证明和推演
- 第8讲 基本命题的构成
- 8.1 基本命题的结构
- 8.2 词项的内涵和外延
- 8.3 词项的种类
- 8.4 词项间的关系
- 8.5 词项的定义
- 8.6 词项的划分
- 8.7 谓词的分类
- 8.8 量词
- 8.9 联词
- 第9讲 传统逻辑中基本命题的推理
- 9.1 基本命题的推理
- 9.2 传统逻辑对基本命题的分析
- 9.3 性质命题中主、谓词的周延
- 9.4 命题变形的推理
- 9.5 根据对当关系的推理
- 9.6 三段论
- 9.7 三段论的式与格
- 9.8 有效三段论的判定
- 第10讲 基本命题的推理
- 10.1 性质命题
- 10.2 主词非空的预设
- 10.3 关系命题的结构
- 10.4 关系命题根据量词的推理
- 10.5 关系命题根据谓词性质的推理方法
- 10.6 谓词演算简介
- 第11讲 非经典逻辑的初步
- 11.1 非经典（非标准）逻辑
- 11.2 多值逻辑
- 11.3 模糊逻辑
- 11.4 模态逻辑
- 11.5 规范逻辑
- 11.6 时态逻辑
- 11.7 弗协调逻辑
- 第12讲 余论
- 12.1 演绎和归纳
- 12.2 探求因果关系的逻辑方法
- 12.3 证论和反驳
- 12.4 悖论
- 12.5 本课程《逻辑学概论》内容回顾