老王自动驾驶规划算法
平台搭建
Prescan配置
C:\Users\Public\Documents\Experiments中有Demo_PreScanCarSim3D.cpar,该文件是与carsim联合仿真的接口
打开Prescan,拖动奥迪A8模型,修改x、y坐标为0
Carsim配置
打开Carsim新建一个库,打开C:\Users\Public\Documents\Experiments中的Demo_PreScanCarSim3D.cpar,并将该文件的动力学数据提取到Experiments下新建的文件DynamicModel中
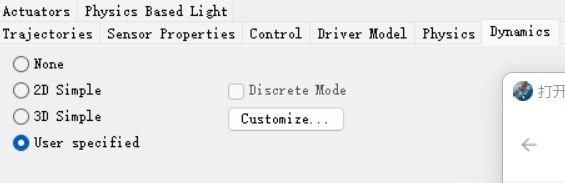
回到Prescan,右键车辆模型选第一个Object···、Dynamics、User specified
选择C:\Users\Public\Documents\Experiments\DynamicModel\Extensions\Simulink中的Carsim_VehicleDynamics.mdl
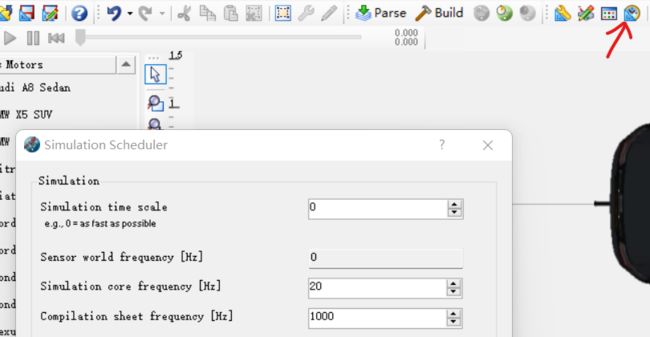
修改仿真频率,修改为20(Prescan感知频率可以低),1000(Carsim的动力学仿真频率需要高)
点击Build,用于生成Simulink模型(testemplanner_cs.slx)
MATLAB配置
通过Prescan任务栏图标打开,右键open,start matlab,自动跳转matlab并进入Experiments路径下
点击浏览文件夹
进入Prescan刚建立的testemplanner文件夹
打开
以后再prescan中做出修改,需要在simulink中点击regenerate,刷新perscan的改动
依次点击以下模块,显示not found,需要添加simfile.sim文件路径:通过carsim中send to simulink会创建一个simfile.sim文件,复制路径到not found的路径中
carsim中设置车辆输入输出
在simulink中打开
查看自带的车辆模型,copy输入和输出到自己的simulink中
在carsim中输出增加ax、ay,send to simulink
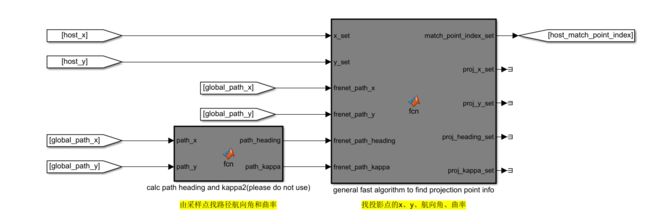
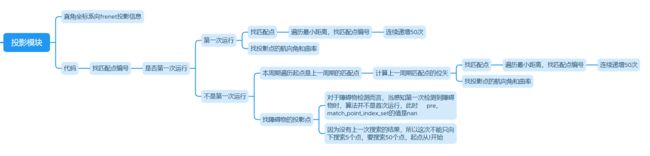
通用投影模块
该函数将批量计算x_set,y_set中的xy,在frenet_path下的投影的信息
%输入 x_set,y_set,待投影的点的集合
frenet_path_x,frenet_path_y,frenet_path_heading,frenet_path_kappa路径参考点的x、y、heading、kappa
%输出:match_point_index_set 匹配点在frenet_path下的编号的集合(即从全局路径第一个点开始数,第几个点是匹配点)
%proj_x y heading kappa 投影的x,y,heading,kappa的集合
参考线算法
routine module,利用prescan导入全局路径
用另一台车跑一遍路径,利用prescan的pathfollow功能和定位获取全局路径
simulink把车辆定位发送至工作空间
先注释控制车,用采集车跑路径
提取路径
把路径点保存为mat文件
在emplanner_init.m中加上导入全局路径命令
注释采集车
把路径点导入控制车中,封装成routine module
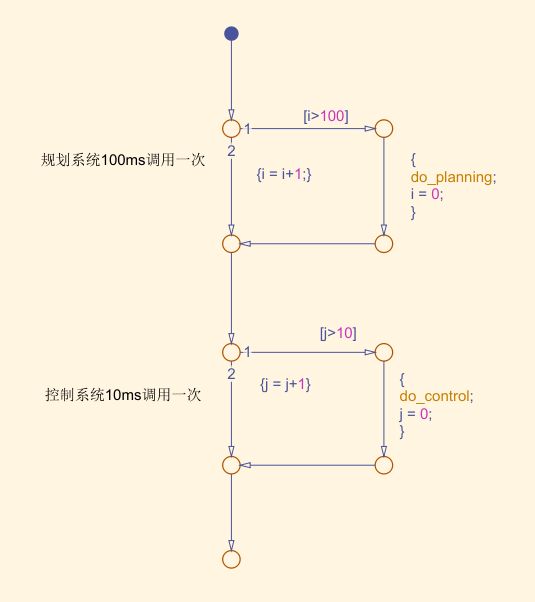
调度系统,加速仿真
Chart状态机写调度系统,确认迭代步长
调度系统配合Trigger(触发器,(function-call模式))一起使用,在planning和control中分别加一个Trigger(function-call模式)
Trigger用离散PID
轨迹拼接模块
function [plan_start_x,plan_start_y,plan_start_heading,plan_start_kappa,plan_start_vx,plan_start_vy,plan_start_ax,...
plan_start_ay,plan_start_time,stitch_x,stitch_y,stitch_heading,stitch_kappa,stitch_speed,stitch_accel,stitch_time] ...
= fcn(pre_trajectory_x,pre_trajectory_y,pre_trajectory_heading,pre_trajectory_kappa,pre_trajectory_velocity,...
pre_trajectory_accel,pre_trajectory_time,current_time,host_x,host_y,host_heading_xy,host_vx,host_vy,host_ax,host_ay)
%该函数将计算规划的起点以及拼接轨迹的信息
%输入 上一周期的规划结果信息pre_trajectory x ,y,heading,kappa,velocity,accel,time
% 本周期的绝对时间current_time
% 定位信息host x,y,heading,kappa,vx,vy,ax,ay
%输出 规划起点信息plan_start x,y,heading,kappa,vx,vy,ax,ay(vx,vy,ax,ay)是世界坐标系的
% 待拼接的轨迹信息,一般在上一周期的轨迹中的current_time+100ms,往前取20个点。
% 当规划完成后,本周期的规划结果和stitch_trajectory一起拼好发给控制
%输出初始化
stitch_x = zeros(20,1);
stitch_y = zeros(20,1);
stitch_heading = zeros(20,1);
stitch_kappa = zeros(20,1);
stitch_speed = zeros(20,1);
stitch_accel = zeros(20,1);
%时间为负代表没有对应的拼接轨迹
stitch_time = ones(20,1)*-1;
%申明全局变量
persistent is_first_run;
if isempty(is_first_run)
%代表代码首次运行
is_first_run = 0;
%按照轨迹拼接算法,应该用车辆动力学递推,但是首次运行车辆的速度都是0,所以没必要递推了,用定位结果
plan_start_x = host_x;
plan_start_y = host_y;
plan_start_heading = host_heading_xy;
plan_start_kappa = 0;
plan_start_vx = 0;
plan_start_vy = 0;
plan_start_ax = 0;
plan_start_ay = 0;
%规划的起点的时间应该是当前时间+100ms
plan_start_time = current_time + 0.1;
else
%该函数不是首次运行
x_cur = host_x;
y_cur = host_y;
heading_cur = host_heading_xy;
kappa_cur = 0;
%vx vy ax ay要转换成世界坐标系
vx_cur = host_vx*cos(heading_cur) - host_vy*sin(heading_cur);
vy_cur = host_vx*sin(heading_cur) + host_vy*cos(heading_cur);
ax_cur = host_ax*cos(heading_cur) - host_ay*sin(heading_cur);
ay_cur = host_ax*sin(heading_cur) + host_ay*cos(heading_cur);
%规划周期
dt = 0.1;
%由于不是首次运行了,有上一时刻的轨迹了,找到上一周期轨迹规划的本周期车辆应该在的位置,得到上一周期规划编号i
for i = 1:length(pre_trajectory_time) - 1
if (pre_trajectory_time(i) <= current_time && pre_trajectory_time(i + 1) > current_time)
break;
end
end
%上一周期规划的本周期的车应该在的位置
pre_x_desire = pre_trajectory_x(i);
pre_y_desire = pre_trajectory_y(i);
pre_heading_desire = pre_trajectory_heading(i);
%计算横纵向误差
%切向量
tor = [cos(pre_heading_desire);sin(pre_heading_desire)];
%法向量
nor = [-sin(pre_heading_desire);cos(pre_heading_desire)];
%误差向量
d_err = [host_x;host_y] - [pre_x_desire;pre_y_desire];
%纵向误差
lon_err = abs(d_err'*tor);
%横向误差
lat_err = abs(d_err'*nor);
%纵向误差大于2.5 横向误差大于0.5 认为控制没跟上
%如果误差仍然存在,则一直执行if,递推规划起点
if (lon_err > 2.5)||(lat_err > 0.5)
%此分支处理控制未跟上的情况,规划起点通过运动学递推,直到控制跟上规划
plan_start_x = x_cur + vx_cur * dt + 0.5 * ax_cur * dt * dt;
plan_start_y = y_cur + vy_cur * dt + 0.5 * ay_cur * dt * dt;
plan_start_vx = vx_cur + ax_cur * dt;
plan_start_vy = vy_cur + ay_cur * dt;
plan_start_heading = atan2(plan_start_vy,plan_start_vx);
plan_start_ax = ax_cur;
plan_start_ay = ay_cur;
plan_start_kappa = kappa_cur;
plan_start_time = current_time + 0.1;
return;
else
%此分支表示控制能跟的上规划,开始拼接;找到下一规划周期的编号j
for j = i:length(pre_trajectory_time) - 1
if (pre_trajectory_time(j) <= current_time + 0.1)&&(pre_trajectory_time(j + 1) > current_time + 0.1)
break;
end
end
%注:此算法要能运行需要trajectory的点有很高的密度
plan_start_x = pre_trajectory_x(j);
plan_start_y = pre_trajectory_y(j);
plan_start_heading = pre_trajectory_heading(j);
plan_start_kappa = pre_trajectory_kappa(j);
%这里的pre_trajectory的速度,加速度是指轨迹的切向速度,切向加速度
plan_start_vx = pre_trajectory_velocity(j) * cos(plan_start_heading);
plan_start_vy = pre_trajectory_velocity(j) * sin(plan_start_heading);
%pre_trajectory的加速度是切向加速度,要想计算ax,ay还要计算法向加速度
%计算轨迹在current_time + 100ms 这个点的切向量法向量
tor = [cos(plan_start_heading);sin(plan_start_heading)];
nor = [-sin(plan_start_heading);cos(plan_start_heading)];
%a_nor = v^2/R= v^2*kappa
a_tor = pre_trajectory_accel(j) * tor;
a_nor = pre_trajectory_velocity(j)^2 * plan_start_kappa * nor ;
%plan_start_ax是世界坐标系,切向加速度与法向加速度在x方向的分量
plan_start_ax = a_tor(1) + a_nor(1);
plan_start_ay = a_tor(2) + a_nor(2);
plan_start_time = pre_trajectory_time(j);
%计算拼接轨迹
%j 表示 current_time + 0.1 的时间点在 pre_trajectory_time的编号
%拼接是往从j开始,往前拼接20个,也就是pre_trajectory(j-1),j-2,j-3,....j-19
%分两种情况,如果j小于20,意味着前面的轨迹点不够20个
%如果j >= 20,意味着前面的点多于20个
%还有一个细节需要考虑,pre_trajectory x(j) y(j) ....是规划的起点,那么在轨迹拼接时
%需不需要在stitch_trajectory中把pre_trajectory x(j) y(j) ....包含进去
%答案是否定的,不应该包进去,因为规划的起点会在规划模块计算完成后的结果中包含,如果在拼接的时候
%还要包含,那就等于规划起点包含了两次
%除非本周期计算的轨迹不包含规划起点,那么stitch_trajectory可以包含规划起点。
%如果本周期计算的轨迹包含规划起点,那么stitch_trajectory就不可以包含规划起点。
%我们选择规划包含起点,拼接不包含起点的做法
%把起点去掉
j = j - 1;
%前面够20个,往前推20个
if j >= 20
stitch_x = pre_trajectory_x(j - 19:j);
stitch_y = pre_trajectory_y(j - 19:j);
stitch_heading = pre_trajectory_heading(j - 19:j);
stitch_kappa = pre_trajectory_kappa(j - 19:j);
stitch_speed = pre_trajectory_velocity(j - 19:j);
stitch_accel = pre_trajectory_accel(j - 19:j);
stitch_time = pre_trajectory_time(j - 19:j);
%不够20个点,有几个拼几个
else
stitch_x(20 - j + 1:20) = pre_trajectory_x(1:j);
stitch_y(20 - j + 1:20) = pre_trajectory_y(1:j);
stitch_heading(20 - j + 1:20) = pre_trajectory_heading(1:j);
stitch_kappa(20 - j + 1:20) = pre_trajectory_kappa(1:j);
stitch_speed(20 - j + 1:20) = pre_trajectory_velocity(1:j);
stitch_accel(20 - j + 1:20) = pre_trajectory_accel(1:j);
stitch_time(20 - j + 1:20) = pre_trajectory_time(1:j);
end
end
end投影s的起点
index2s算法:以车辆定位向referenceline的投影点为s的起点,得到各障碍物的位置信息
function index2s = fcn(path_x,path_y,origin_x,origin_y,origin_match_point_index)
%该函数将输出index与s的转换关系,index2s表示当path_x,path_y的离散点的编号为i时,对应的弧长为index2s(i)
%输入 path_x path_y 是reference平滑后的离散点集合
% origin_x,y frenet投影点在世界坐标系下的信息
% origin_match_point_index 原点的匹配点的编号
% path点的个数
n = 181;
% 输出初始化
index2s = zeros(n,1);
% 首先计算以path起点为坐标原点的index2s
for i = 2:n
index2s(i) = sqrt((path_x(i) - path_x(i-1))^2 + (path_y(i) - path_y(i-1))^2) + index2s(i-1);
end
% 再计算以轨迹起点到frenet_path的坐标原点的弧长,记为s0,再用index2s - s0 就是最终的结果
% 计算s0
% s_temp frenet原点的匹配点的弧长
s_temp = index2s(origin_match_point_index);
%判断原点在匹配点的前面还是后面
%两个向量match_point_to_origin
% match_point_to_match_point_next
vector_match_2_origin = [origin_x;origin_y] - [path_x(origin_match_point_index);path_y(origin_match_point_index)];
vector_match_2_match_next = [path_x(origin_match_point_index + 1);path_y(origin_match_point_index + 1)] - ...
[path_x(origin_match_point_index);path_y(origin_match_point_index)];
if vector_match_2_origin'*vector_match_2_match_next > 0
%坐标原点在匹配点的前面
s0 = s_temp + sqrt(vector_match_2_origin'*vector_match_2_origin);
else
%坐标原点在匹配点的后面
s0 = s_temp - sqrt(vector_match_2_origin'*vector_match_2_origin);
end
index2s = index2s - ones(n,1)*s0;坐标转换
计算S、L
function [s_set,l_set] = fcn(x_set,y_set,frenet_path_x,frenet_path_y,...
proj_x_set,proj_y_set,proj_heading_set,proj_match_point_index_set,index2s)
%该函数将计算世界坐标系下的x_set,y_set上的点在frenet_path下的坐标s l
%输入 x_set,y_set 待坐标转换的点
% frenet_path_x,frenet_path_y frenet坐标轴
% proj_x,y,heading,kappa,proj_match_point_index 待坐标转换的点的投影点的信息
% index2s frenet_path的index与s的转换表
% 由于不知道有多少个点需要做坐标转换,所以需要做缓冲
n = 128;%最多处理128个点
%输出初始化
s_set = ones(n,1)*nan;
l_set = ones(n,1)*nan;
for i = 1:length(x_set)
if isnan(x_set(i))
break;
end
%计算s,写个子函数
s_set(i) = CalcSFromIndex2S(index2s,frenet_path_x,frenet_path_y,proj_x_set(i),proj_y_set(i),...
proj_match_point_index_set(i));
n_r = [-sin(proj_heading_set(i));cos(proj_heading_set(i))];
r_h = [x_set(i);y_set(i)];
r_r = [proj_x_set(i);proj_y_set(i)];
l_set(i) = (r_h - r_r)'*n_r;
end
end
function s = CalcSFromIndex2S(index2s,path_x,path_y,proj_x,proj_y,proj_match_point_index)
%该函数将计算当指定index2s的映射关系后,计算点proj_x,proj_y的弧长
vector_1 = [proj_x;proj_y] - [path_x(proj_match_point_index);path_y(proj_match_point_index)];
%这里要考虑的更全面一些,因为要考虑到proj_match_point_index有可能在path的起点或终点
if (proj_match_point_index < length(path_x))
vector_2 = [path_x(proj_match_point_index + 1);path_y(proj_match_point_index + 1)] - ...
[path_x(proj_match_point_index);path_y(proj_match_point_index)];
else
vector_2 = [path_x(proj_match_point_index);path_y(proj_match_point_index)] - ...
[path_x(proj_match_point_index - 1);path_y(proj_match_point_index - 1)];
end
if vector_1'*vector_2 > 0
s = index2s(proj_match_point_index) + sqrt(vector_1'*vector_1);
else
s = index2s(proj_match_point_index) - sqrt(vector_1'*vector_1);
end
end计算S'、L'、L''
function [s_dot_set,l_dot_set,dl_set] = fcn(l_set,vx_set,vy_set,proj_heading_set,proj_kappa_set)
%该函数将计算frenet坐标系下的s_dot, l_dot, dl/ds
n = 128;
% 输出初始化
s_dot_set = ones(n,1)*nan;
l_dot_set = ones(n,1)*nan;
dl_set = ones(n,1)*nan;
for i = 1 : length(l_set)
if isnan(l_set(i))
break;
end
v_h = [vx_set(i);vy_set(i)];
n_r = [-sin(proj_heading_set(i));cos(proj_heading_set(i))];
t_r = [cos(proj_heading_set(i));sin(proj_heading_set(i))];
l_dot_set(i) = v_h'*n_r;
s_dot_set(i) = v_h'*t_r/(1 - proj_kappa_set(i)*l_set(i));
%%%向量法做cartesian与frenet的转换要更简单,但是也有缺点,向量法必须依赖速度加速度
%l' = l_dot/s_dot 但是如果s_dot = 0 此方法就失效了
if abs(s_dot_set(i)) < 1e-6
dl_set(i) = 0;
else
dl_set(i) = l_dot_set(i)/s_dot_set(i);
end
end计算S''、L''
function [s_dot2_set,l_dot2_set,ddl_set] = fcn(ax_set,ay_set,proj_heading_set,proj_kappa_set,l_set,s_dot_set,dl_set)
%由于不知道有多少个点需要做坐标转换,设一个最大值做缓冲
n = 128;
% 输出初始化
s_dot2_set = ones(n,1)*nan;
l_dot2_set = ones(n,1)*nan;
ddl_set = ones(n,1)*nan;
for i = 1:length(l_set)
if isnan(l_set(i))
break;
end
a_h = [ax_set(i);ay_set(i)];
n_r = [-sin(proj_heading_set(i));cos(proj_heading_set(i))];
t_r = [cos(proj_heading_set(i));sin(proj_heading_set(i))];
%近似认为dkr/ds 为0 简化计算
l_dot2_set(i) = a_h'*n_r - proj_kappa_set(i) * (1 - proj_kappa_set(i) * l_set(i)) * s_dot_set(i)^2;
s_dot2_set(i) = (1/(1 - proj_kappa_set(i) * l_set(i)))* (a_h' * t_r + 2 * proj_kappa_set(i) * dl_set(i) * s_dot_set(i)^2);
% 要考虑加速度为0的情况
if (s_dot2_set(i) < 1e-6)
ddl_set(i) = 0;
else
ddl_set(i) = (l_dot2_set(i) - dl_set(i)*s_dot2_set(i))/(s_dot_set(i)^2);
end
end障碍物投影
动态规划算法
本节是以参考线为S,横向偏移为L进行计算
end_l = ((row + 1)/2 - cur_node_row)*sample_l是指:
row相对于中间行(参考线所在行)的偏移量L
function [dp_path_s,dp_path_l] = fcn(obs_s_set,obs_l_set,plan_start_s,plan_start_l,plan_start_dl,...
plan_start_dll,w_cost_collision,w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,row,col,sample_s,sample_l)
%该函数为路径决策算法动态规划的主函数
% 输入:obs s l set 筛选后的障碍物sl信息
% plan_start s l dl ddl 规划起点信息
% w_cost_obs,w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref动态规划代价权重
% row col 动态规划采样点的行数和列数(row必须是奇数,col必须是6)
% sample_s,sample_l 采样的s l 长度
% 输出:dp_path_l,dp_path_s 动态规划的路径sl,此路径不包含规划起点
%动态规划最优的数据结构是结构体矩阵,但是simulink不支持结构体矩阵,所以动态规划算法写的相对难以理解
%声明二维矩阵变量node_cost,node_cost(i,j)表示从起点出发,到行i列j节点的最小代价为node_cost(i,j)
node_cost = ones(row,col)*inf;%初始化为无穷大
%声明二维矩阵变量pre_node_index pre_node_index(i,j)表示从起点到行i列j的节点的最优路径中前一个节点的行号为
%pre_node_index(i,j)
%例:比如一条最优路径为 起点 -> node(1,1) -> node(2,2) -> node(3,3)
%则pre_node_index(3,3) = 2 (最优路径的前一个节点是node(2,2) 取它的行号)
% pre_node_index(2,2) = 1 (最优路径的前一个节点是node(1,1) 取它的行号)
% pre_node_index(1,1) = 0 (起点的行号默认是0)
% 其实pre_node_index就是当找到最小代价的路径后从终点到起点反向选择出最优路径的
%如果用结构体矩阵完全没有必要弄得这么麻烦,但是simulink不支持
pre_node_index = zeros(row,col);%初始化,所有节点的上个最优节点的行号都是0,也就是起点
%先计算从起点到第一列的cost
for i = 1:row
node_cost(i,1) = CalcStartCost(plan_start_s,plan_start_l,plan_start_dl,...
plan_start_dll,i,sample_s,sample_l,w_cost_collision,w_cost_smooth_dl,...
w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set,row);
end
% 动态规划主函数,从第二列开始
for j = 2:col
for i = 1:row
%计算当前node(i,j)的s l
cur_node_s = plan_start_s + j * sample_s;
cur_node_l = ((row + 1)/2 - i) * sample_l;
%遍历前一列的节点
for k = 1:row
%计算前一列节点的s l
pre_node_s = plan_start_s + (j - 1) * sample_s;
pre_node_l = ((row + 1)/2 - k) * sample_l;
cost_neighbour = CalcNeighbourCost(pre_node_s,pre_node_l,cur_node_s,cur_node_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set);
%起点到上一个节点的最小代价为node_cost(k,j-1)
pre_min_cost = node_cost(k,j-1);
%起点到node_cost(i,j)的最小代价 为node_cost(k,j-1)
%再加上node(k,j-1)到node(i,j)的代价 (k = 1,2,3,4...row) 中最小的
cost_temp = pre_min_cost + cost_neighbour;
if cost_temp < node_cost(i,j)
node_cost(i,j) = cost_temp;
%把最优路径上一列节点的行号记录下来
pre_node_index(i,j) = k;
end
end
end
end
%找到node_cost最后一列中,cost最小的,记代价最小的行号为index
index = 0;
min_cost = inf;
for i = 1:row
if node_cost(i,end) < min_cost
min_cost = node_cost(i,end);
index = i;
end
end
%动态规划最优路径初始化
dp_node_list_row = zeros(col,1);
%从后往前逆推
cur_index = index;
for i = 1:col
%记录cur_index前面节点的行号
pre_index = pre_node_index(cur_index,end - i + 1);
%把cur_index放到dp_node_list_row对应的位置
dp_node_list_row(col - i + 1) = cur_index;
%再把pre_index 赋给 cur_index 进行下一步递推
cur_index = pre_index;
end
% 输出初始化,由于事先不知道横纵向的采样列数,因此需要做缓冲
dp_path_s = ones(15,1)*-1;
dp_path_l = ones(15,1)*-1;
for i = 1:col
dp_path_s(i) = plan_start_s + i * sample_s;
dp_path_l(i) = ((row + 1) / 2 - dp_node_list_row(i)) * sample_l;
end
end
function cost = CalcNeighbourCost(pre_node_s,pre_node_l,cur_node_s,cur_node_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set)
% 该函数将计算相邻两个节点之间的cost
start_l = pre_node_l;
start_dl = 0;
start_ddl = 0;
end_l = cur_node_l;
end_dl = 0;
end_ddl = 0;
start_s = pre_node_s;
end_s = cur_node_s;
coeff = CalcQuinticCoeffient(start_l,start_dl,start_ddl,end_l,end_dl,end_ddl,start_s,end_s);
a0 = coeff(1);
a1 = coeff(2);
a2 = coeff(3);
a3 = coeff(4);
a4 = coeff(5);
a5 = coeff(6);
% 取10个点计算cost
ds = zeros(10,1);
l = zeros(10,1);
dl = zeros(10,1);
ddl = zeros(10,1);
dddl = zeros(10,1);
for i = 1:10
ds(i) = start_s + (i-1)*(end_s - start_s)/10;
end
l = a0 * ones(10,1) + a1 * ds + a2 * ds.^2 + a3 * ds.^3 + a4 * ds.^4 + a5 * ds.^5;
dl = a1 * ones(10,1) + 2 * a2 * ds + 3 * a3 * ds.^2 + 4 * a4 * ds.^3 + 5 * a5 * ds.^4;
ddl = 2 * a2 * ones(10,1) + 6 * a3 * ds + 12 * a4 * ds.^2 + 20 * a5 * ds.^3;
dddl = 6 * ones(10,1) * a3 + 24 * a4 * ds + 60 * a5 * ds.^2;
cost_smooth = w_cost_smooth_dl * (dl' * dl) + w_cost_smooth_ddl * (ddl' * ddl) + w_cost_smooth_dddl * (dddl' * dddl);
cost_ref = w_cost_ref * (l' * l);
cost_collision = 0;
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
dlon = ones(10,1) * obs_s_set(i) - ds;
dlat = ones(10,1) * obs_l_set(i) - l;
%这里做了非常简化的质点模型,认为障碍物就是一个点
square_d = dlon.^2 + dlat.^2;
cost_collision_once = CalcObsCost(w_cost_collision,square_d);
cost_collision = cost_collision + cost_collision_once;
end
cost = cost_collision + cost_smooth + cost_ref;
end
function cost = CalcStartCost(begin_s,begin_l,begin_dl,begin_ddl,cur_node_row,sample_s,sample_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set,row)
%该函数将计算起点到第一层的cost
start_l = begin_l;
start_dl = begin_dl;
start_ddl = begin_ddl;
% . . .
% . . . row = 3 中间的行号 = (row + 1) /2 = 2
% . . .
end_l = ((row + 1)/2 - cur_node_row)*sample_l;
end_dl = 0;
end_ddl = 0;
start_s = begin_s;
end_s = begin_s + sample_s;
coeff = CalcQuinticCoeffient(start_l,start_dl,start_ddl,end_l,end_dl,end_ddl,start_s,end_s);
a0 = coeff(1);
a1 = coeff(2);
a2 = coeff(3);
a3 = coeff(4);
a4 = coeff(5);
a5 = coeff(6);
% 取10个点计算cost
ds = zeros(10,1);
l = zeros(10,1);
dl = zeros(10,1);
ddl = zeros(10,1);
dddl = zeros(10,1);
for i = 1:10
ds(i) = start_s + (i-1)*sample_s/10;
end
l = a0 * ones(10,1) + a1 * ds + a2 * ds.^2 + a3 * ds.^3 + a4 * ds.^4 + a5 * ds.^5;
dl = a1 * ones(10,1) + 2 * a2 * ds + 3 * a3 * ds.^2 + 4 * a4 * ds.^3 + 5 * a5 * ds.^4;
ddl = 2 * a2 * ones(10,1) + 6 * a3 * ds + 12 * a4 * ds.^2 + 20 * a5 * ds.^3;
dddl = 6 * ones(10,1) * a3 + 24 * a4 * ds + 60 * a5 * ds.^2;
cost_smooth = w_cost_smooth_dl * (dl' * dl) + w_cost_smooth_ddl * (ddl' * ddl) + w_cost_smooth_dddl * (dddl' * dddl);
cost_ref = w_cost_ref * (l' * l);
cost_collision = 0;
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
dlon = ones(10,1) * obs_s_set(i) - ds;
dlat = ones(10,1) * obs_l_set(i) - l;
%这里做了非常简化的质点模型,认为障碍物就是一个点
square_d = dlon.^2 + dlat.^2;
cost_collision_once = CalcObsCost(w_cost_collision,square_d);
cost_collision = cost_collision + cost_collision_once;
end
cost = cost_collision + cost_smooth + cost_ref;
end
function obs_cost = CalcObsCost(w_cost_collision,square_d)
%该函数将计算障碍物的距离代价
% 暂定超过4米的cost为0 在4到3米的cost为1000/squard_d,在小于3米的cost为w_cost_collision
cost = 0;
for i = 1:length(square_d)
if (square_d(i) < 16 && square_d(i) > 9)
cost = cost + 1000/square_d(i);
elseif (square_d(i) < 9)
cost = cost + w_cost_collision;
end
end
obs_cost = cost;
end
function coeff = CalcQuinticCoeffient(start_l,start_dl,start_ddl,end_l,end_dl,end_ddl,start_s,end_s)
% l = a0 + a1*s + a2*s^2 + a3*s^3 + a4*s^4 + a5*s^5
% l' = a1 + 2 * a2 * s + 3 * a3 * s^2 + 4 * a4 * s^3 + 5 * a5 * s^4
% l'' = 2 * a2 + 6 * a3 * s + 12 * a4 * s^2 + 20 * a5 * s^3
start_s2 = start_s * start_s;
start_s3 = start_s2 * start_s;
start_s4 = start_s3 * start_s;
start_s5 = start_s4 * start_s;
end_s2 = end_s * end_s;
end_s3 = end_s2 * end_s;
end_s4 = end_s3 * end_s;
end_s5 = end_s4 * end_s;
A = [1,start_s, start_s2, start_s3, start_s4, start_s5;
0 1, 2 * start_s, 3 * start_s2, 4 * start_s3, 5 * start_s4;
0 0, 2, 6 * start_s, 12 * start_s2, 20 * start_s3;
1,end_s, end_s2, end_s3, end_s4, end_s5;
0,1, 2 * end_s, 3 * end_s2, 4 * end_s3, 5 * end_s4;
0,0, 2, 6 * end_s, 12 * end_s2, 20 * end_s3;];
B = [start_l;
start_dl;
start_ddl;
end_l;
end_dl;
end_ddl;];
coeff = A \ B;
end错误汇总
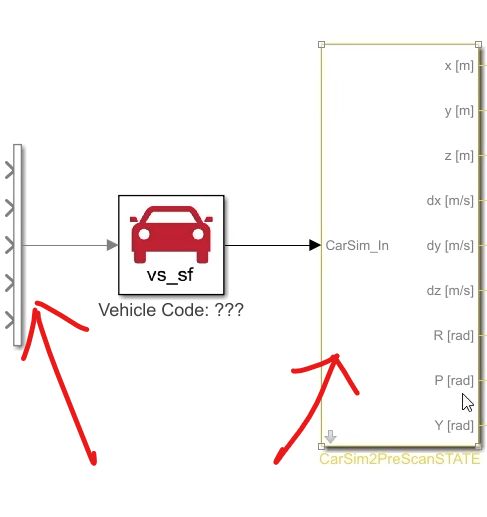
错误: S-Function模块出现CarSim S-Function2 ,CarSim S-Function Vehicle Code:???
解决方法:
修改matlab目录,修复simulink缺失模块
在matlab中设置路径,添加solves文件夹(一般在carsim安装目录的\Programs\solvers)
打开simulink的Library Browser,按F5刷新,提示Some libraries are missing repository information. (如果没有的话,在左侧框内右键,刷新一下菜单Refresh Library Browser)
点击Fix,选择'Generate repositories in memory',ok。此时,S-Function模块添加进来了。
修改S-Function模块错误
模块错误显示如下:
第一行的CarSim S-Function2 去掉2
双击模块后(此时只有Source block,没有Simfile name),将Source block中修改为:Solver_SF/CarSim S-Function,图标会修改为正常样式:
此时出现了Simfile name,修改路径为carsim提取prescan的动力学模型数据的文件下:C:\Users\Public\Documents\Experiments\DynamicModel\Simfile.sim
错误:函数或者变量KP_PID_distance"无法识别"
需要先运行emplanner_init.m,把油门刹车程序标定运行
运行步骤
运行emplanner_init.m,标定油门刹车
matlab命令行执行vs_state = -1,stopmode = -1