Unity 游戏优化:空间分区
游戏优化之空间分区
- 〇. 前言
-
- 1. Unity 中的碰撞检测机制
- 2. 平面四叉树
- 一. 四叉树的具体实现步骤
-
- 1. 四叉树本体
- 2. 四叉树节点
- 3. 数值范围
- 4. 节点字典
- 5. 代码优化
- 二. 空间分区的具体实现步骤
-
- 1. 空间单元
- 2. 界定范围
- 3. 空间分区脑
〇. 前言
受启于[空间分区·Optimization Patterns·游戏模式].
>> 前言部分文章的原文链接如下 << [深入理解Unity的碰撞检测机制] (http://www.manew.com/thread-102595-1-1.html).
1. Unity 中的碰撞检测机制
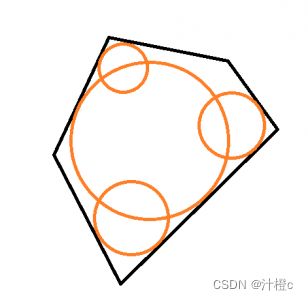
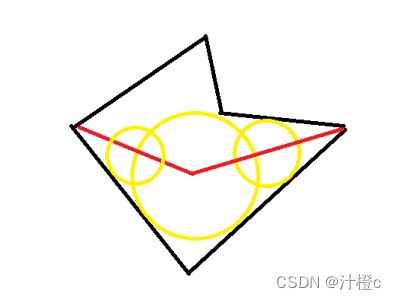
碰撞检测,就是检测两个物体是否相交,如果物体非常规则,比如球体,直接检测圆心距离是否小于半径和即可,计算量十分小。但是,如果物体不规则(比如一个角色,进行十分细致的碰撞检测就会变的十分困难),我们一般会用简单几何体去逼近复杂网格,如下图:
注意:下层圆圆心位于根圆到顶点连线上,且圆心位于上层圆边上的。类比到3d空间也是如此,可以用球体去趋近网格。这里需要注意,凹多边形的逼近是难计算的,所以内部会将其拆分成多个凸多边形。
对于我本人的理解,这段话中根圆和下层圆,可以类比于树结构中的根节点与根节点下一层的节点。
不同精度的碰撞决定着树的层数!
为了解决这个问题,unity里使用了空间划分技术,目前主流的划分技术有BSP,BHV,八叉树,四叉树
这几种算法都用到了树结构。
>> 更详细的内容见原文。[深入理解Unity的碰撞检测机制].
2. 平面四叉树
四元树又称四叉树是一种树状数据结构,在每一个节点上会有四个子区块。四元树常应用于二维空间数据的分析与分类。 它将数据区分成为四个象限。数据范围可以是方形或矩形或其他任意形状。
看完上面描述,我们可以把四叉树分为以下部分编写:
四叉树本体: 有一个四叉树根节点,一个节点分支层数上限数值,如果要在遍历的时候更方便的查改,可以再添加一个储存节点和值的节点字典。
四叉树节点: 储存值和数据范围,属性有子节点和父节点。
数值范围: 用于数据划分和检测。
节点字典(如果要经常查改): 用于储存值和节点键对的字典,方便通过指定值查找节点,或通过指定节点查找值。
一. 四叉树的具体实现步骤
1. 四叉树本体
按照正常的写树结构那样写下去,没有其他技巧。
增删查改按需修改(如果想提高这些功能的可拓展性,可以试着用委托代理替换增删查改)。
public class QuadTree<T, TNode, TRange>
where TNode : QuadTree<T, TNode, TRange>.QuadTreeNode<TNode>
where TRange : QuadTree<T, TNode, TRange>.DataRange
{
// 根节点
protected TNode m_Root = null;
// 数据范围检测的方法,如果 T 超出 TRange 范围,则返回 false
protected System.Func<T, TRange, bool> m_InRangeJudgement;
// 不能无限分区,限定一个最小范围
protected TRange m_MinRange;
// 范围内的物体超过该数,则分区
protected int m_UltimateStack = 3;
public bool IsNullOrEmpty => m_Root == null;
protected QuadNodeDictionary NodeDic { get; set; }
/// 添加成功布尔
public bool Add(T t)
{
AddingProgress progress = AddFrom_Injected(m_Root, t, out TNode splitBeforeNode);
switch (progress)
{
case AddingProgress.Fit:
NodeDic.Add(t, splitBeforeNode);
return true;
case AddingProgress.NeedDivide:
NodeDic.Remove(splitBeforeNode);
splitBeforeNode.ForEachLeaf(
(node) =>
{
if (!node.IsEmpty)
NodeDic.Add(node.Values, node);
return true;
});
return true;
case AddingProgress.Failures:
default:
return false;
}
}
/// 移除成功布尔
public bool Remove(T t)
{
RemovingProgress progress;
TNode finalParentNode = null;
if (NodeDic.TryGetNode(t, out TNode curNode)) // 如果可以获取到 t 所在的区域,则移除成功
progress = RemoveFrom_Injected(curNode, t, out finalParentNode);
else // 如果不能够获取到 t 所在的区域,则移除失败
progress = RemovingProgress.Failures;
switch (progress)
{
case RemovingProgress.Success:
NodeDic.Remove(t);
return true;
case RemovingProgress.NeedMerge:
// 移除所有先前的 value 键对(移除 和 "merge 之前的 value" 配对的 node)
NodeDic.Remove(finalParentNode.Values);
NodeDic.Remove(t);
// 添加现在的 value 键对(和 merge 后的 node 配对)
NodeDic.Add(finalParentNode.Values, finalParentNode);
return true;
case RemovingProgress.Failures:
default:
return false;
}
}
public bool Contains(T t)
{
return NodeDic.Contains(t);
}
/// 不要全部 T 更新完再 Move,要每个更新独自 Move
/// 移动成功布尔
public bool Move(T t)
{
// 1. 在区域内寻找 t,找不到则返回
if (!NodeDic.TryGetNode(t, out TNode curNode))
{
this.Add(t);
return true;
}
// 2. 检测 t 是否在原节点的范围外,如果在范围外,则移除并重新添加 t
if (!m_InRangeJudgement(t, curNode.Range))
{
// 先移除
this.Remove(t);
// 再添加
this.Add(t);
return true;
}
return true;
}
#endregion
#region 内部方法
/// 返回添加的最后状态
protected AddingProgress AddFrom_Injected(TNode curNode, T t, out TNode splitBeforeNode)
{
// 1. 如果元素不在范围内,则添加失败
if (!m_InRangeJudgement(t, curNode.Range))
{
splitBeforeNode = curNode;
return AddingProgress.Failures;
}
// 2. 获取 t 所在的当前不可再划分的区域
curNode = GetLeafNode_Injected(curNode, t);
// 3. 在此区域添加该元素
curNode.AddValue(t);
splitBeforeNode = curNode;
// 4. 如果数量超过最大堆叠数,则分区
if (CheckDivideQuad_Injected(curNode))
return AddingProgress.NeedDivide;
else
return AddingProgress.Fit;
}
/// 返回移除的最后状态
protected RemovingProgress RemoveFrom_Injected(TNode curNode, T t, out TNode mergeParentNode)
{
// 1. 在此区域移除该元素
curNode.RemoveValue(t);
mergeParentNode = curNode;
// 2. 如果数量低于最大堆叠数,则合并
if (CheckMergeQuad_Injected(ref mergeParentNode))
return RemovingProgress.NeedMerge;
else
return RemovingProgress.Success;
}
/// 符合 t 的区域范围内的 QuadTreeNode
protected TNode GetLeafNode_Injected(TNode curNode, T t)
{
// 如果元素在已经分区过的区域,则递归子区域(寻找 t 所在的范围的区域),直到元素所在区域没有被分区过
while (curNode.IsDivided)
{
curNode.ForEachChild(
(node) =>
{
bool inRange = m_InRangeJudgement(t, node.Range);
if (inRange)
curNode = node;
return !inRange;
});
}
return curNode;
}
/// 只要有进行过分区,就返回 true
protected bool CheckDivideQuad_Injected(TNode curNode)
{
// 如果 "物品数量超过或等于最大堆叠数" 且 "区域范围大于等于最小范围" ,则分区
if (curNode.Count >= m_UltimateStack && curNode.Range.CompareTo(m_MinRange) >= 0)
{
curNode.Divide(m_InRangeJudgement);
bool needDivide = false;
curNode.ForEachChild(
(child) =>
{
needDivide = CheckDivideQuad_Injected(child);
return !needDivide;
});
return true;
}
else
return false;
}
/// 只要有进行过合并,就返回 true
protected bool CheckMergeQuad_Injected(ref TNode curNode)
{
TNode parent = curNode.Parent;
if (parent == null)
return false;
// 如果父节点的物品数量低于最大堆叠数,则合并
if (parent.Count < m_UltimateStack)
{
parent.Merge();
curNode = parent;
CheckMergeQuad_Injected(ref curNode);
return true;
}
else
return false;
}
#endregion
#region 其他公开方法
public void ForEachValue(System.Action<T> valueAction)
{
NodeDic.ForEachT(valueAction);
}
/// 仅仅遍历最底部的 range
public void ForEachRange(System.Action<TRange> rangeAction)
{
if(m_Root != null)
{
m_Root.ForEachLeaf(
node =>
{
rangeAction(node.Range);
return true;
});
}
}
#endregion
public enum AddingProgress
{
Failures,
NeedDivide,
Fit,
}
public enum RemovingProgress
{
Failures,
NeedMerge,
Success,
}
}
2. 四叉树节点
有父节点和子节点(子节点变成子节点组),可以储存多个值。有数据分区和合并的方法(按照数据范围分区和合并)。
该类是 QuadTree 的内部类。
public class QuadTreeNode<TInheritNode> : NodeFactory<TInheritNode, TRange>, IParentNode<TInheritNode>
where TInheritNode : QuadTreeNode<TInheritNode>
{
protected TInheritNode[] childs;
protected List<T> m_Values;
protected TRange m_Range;
protected TInheritNode[] Childs => childs;
public TInheritNode Parent { get; set; }
/// 进行过分区 [Childs != null && Childs.Length != 0]
public bool IsDivided => Childs != null && Childs.Length != 0;
/// 物品的数量是否为空 [m_Values == null || m_Values.Count == 0]
public bool IsEmpty => m_Values == null || m_Values.Count == 0;
public TRange Range => m_Range;
/// 获取自己的所有的 value,如果已经有子节点,则返回空列表
public List<T> Values => m_Values;
/// 获取 value 的数量
public int Count
{
get
{
if (!IsDivided)
{
if (IsEmpty)
{
return 0;
}
return m_Values.Count;
}
else
{
int count = 0;
foreach (TInheritNode child in Childs)
count += child.Count;
return count;
}
}
}
private QuadTreeNode(System.Func<TRange, TInheritNode> nodeProductor) : base(nodeProductor)
{
}
public QuadTreeNode(TRange range, System.Func<TRange, TInheritNode> nodeProductor)
: this(nodeProductor)
{
this.m_Range = range;
}
public QuadTreeNode(T value, TRange range, System.Func<TRange, TInheritNode> nodeProductor)
: this(nodeProductor)
{
this.m_Range = range;
this.AddValue(value);
}
#region 对 Values 的增删查改
public void AddValue(T value)
{
m_Values ??= new List<T>();
m_Values.Add(value);
}
public void AddValues(IEnumerable<T> values)
{
this.m_Values ??= new List<T>();
this.m_Values.AddRange(values);
}
public bool RemoveValue(T value)
{
return m_Values.Remove(value);
}
public bool ContainsValue(T value)
{
return m_Values.Contains(value);
}
#endregion
/// 3. 数值范围
数据范围可分割。
该类是 QuadTree 的内部类。
// TImpleRange 是 IRange 的实现类,实现接口内部抽象方法等
public interface IRanged<TImpleRange> where TImpleRange : IRanged<TImpleRange>
{
public TImpleRange[] Divide();
}
// 数据范围类,TRange 必须是 DataRange 的继承类
// 以重写和实现内部具体方法
// 拓展性较高
public abstract class DataRange : IRanged<TRange>, System.IComparable<TRange>
{
// 用于储存已经分开的数据范围(由一个大的范围分成四个小范围)
private TRange[] m_DividedRanges;
public TRange GetRange(int index)
{
if (m_DividedRanges == null || m_DividedRanges.Length != 4)
{
m_DividedRanges = Divide();
}
// 索引越界的异常捕捉
if (index < 0 || index >= m_DividedRanges.Length)
{
throw new System.ArgumentOutOfRangeException();
}
return m_DividedRanges[index];
}
public abstract TRange[] Divide();
public abstract int CompareTo(TRange other);
}
4. 节点字典
封装值和节点的字典。
该类是 QuadTree 的内部类。
public class QuadNodeDictionary
{
private readonly Dictionary<T, TNode> m_NodeDic;
public QuadNodeDictionary()
{
m_NodeDic = new Dictionary<T, TNode>();
}
// 封装 Dictionary 的常用方法(增删查改)……
// ……
}
5. 代码优化
以下是工厂类的代码,以减少对 new 的直接使用,将创建的方法更友好的展现在眼前。
// 节点工厂(自产自销,减少直接对 new 的使用)
public class NodeFactory<Prod, Param1> : INodeFactory<Prod, Param1>
{
private readonly System.Func<Param1, Prod> m_NodeProductor;
protected NodeFactory(System.Func<Param1, Prod> nodeProductor)
{
m_NodeProductor = nodeProductor;
}
public Prod Create(Param1 p1)
{
return m_NodeProductor(p1);
}
}
// 自产自销工厂接口
public interface INodeFactory<Prod, Param1>
{
public Prod Create(Param1 p1);
}
二. 空间分区的具体实现步骤
1. 空间单元
由于具体的方法在 QuadTree 中都实现了,继承类直接继承就好了。
public class SpaceUnit_2D : QuadTree<Transform, SpaceUnitNode , SpaceRange_2D>
{
public SpaceUnit_2D(int ultimateStack, SpaceRange_2D unitRange, SpaceRange_2D minRange, Func<Transform, SpaceRange_2D, bool> inRangeJudgement)
: base(ultimateStack, unitRange, minRange, inRangeJudgement)
{
m_Root = new QuadTreeNode(unitRange);
}
public sealed class SpaceUnitNode : QuadTreeNode<SpaceUnitNode >
{
public QuadTreeNode(SpaceRange_2D range)
: base(range, r => new QuadTreeNode(r))
{
}
public QuadTreeNode(T value, SpaceRange_2D range)
: base(value, range, r => new SpaceUnitNode (r))
{
}
}
}
2. 界定范围
二维空间下的界定范围。
[System.Serializable]
public class SpaceRange_2D : SpaceUnit_2D.DataRange
{
// 矩形范围的中心
[SerializeField] private Vector2 m_Center;
// 矩形范围的大小
[SerializeField] private Vector2 m_Size;
// 矩形范围的边界值
private float[] Edges { get; set; }
public Vector2 Center => m_Center;
public Vector2 Size => m_Size;
public SpaceRange_2D(Vector2 center, Vector2 size)
{
this.m_Center = center;
this.m_Size = size;
RecalcuEdge();
}
public SpaceRange_2D(float x, float y, uint width, uint height)
{
this.m_Center = new Vector2(x, y);
this.m_Size = new Vector2(width, height);
RecalcuEdge();
}
// 重新计算边界
public void RecalcuEdge()
{
Edges = new float[]
{
Center.x - Size.x * 0.5f,
Center.y - Size.y * 0.5f,
Center.x + Size.x * 0.5f,
Center.y + Size.y * 0.5f,
};
}
// 数据范围进行分区处理
public override SpaceRange_2D[] Divide()
{
Vector2 quadSize = Size * 0.25f;
Vector2[] centers = new Vector2[]
{
new Vector2(Center.x + quadSize.x,Center.y + quadSize.y),
new Vector2(Center.x - quadSize.x,Center.y + quadSize.y),
new Vector2(Center.x - quadSize.x,Center.y - quadSize.y),
new Vector2(Center.x + quadSize.x,Center.y - quadSize.y),
};
Vector2 sizes = Size * 0.5f;
SpaceRange_2D[] ranges = new SpaceRange_2D[4];
for (int i = 0; i < 4; i++)
{
ranges[i] = new SpaceRange_2D(centers[i], sizes);
}
return ranges;
}
// 数据范围之间互相比较的方法
public override int CompareTo(SpaceRange_2D other)
{
if (this.Size == other.Size)
{
return 0;
}
if (this.Size.x < other.Size.x && this.Size.y < other.Size.y)
{
return -1;
}
if (this.Size.x > other.Size.x && this.Size.y > other.Size.y)
{
return 1;
}
return int.MinValue;
}
// 重新计算边界的静态方法
public static void RecalcuEdge(SpaceRange_2D range)
{
range.RecalcuEdge();
}
// 判断三维坐标是否在边界内的方法
public static bool IsInside(Vector3 position, SpaceRange_2D range)
{
return IsInside(new Vector2(position.x, position.z), range);
}
// 判断二维坐标是否在边界内的方法
public static bool IsInside(Vector2 position, SpaceRange_2D range)
{
if (range == null)
{
DebugHelper.Message.Log("range 不存在!");
return false;
}
if (range.Edges == null || range.Edges.Length == 0)
{
range.RecalcuEdge();
if (range.Edges == null || range.Edges.Length == 0)
{
DebugHelper.Message.Log("range 的 edge 不存在或长度为 0!");
return false;
}
}
return position.x >= range.Edges[0] && position.y >= range.Edges[1]
&& position.x <= range.Edges[2] && position.y <= range.Edges[3];
}
}
3. 空间分区脑
静态空间分区的控制总部。
public class SpatialPartition_2D : MonoBehaviour
{
[SerializeField, Min(3)] private int m_UltimateStack = 3;
[SerializeField] private SpaceRange_2D m_UnitRange;
[SerializeField] private SpaceRange_2D m_MinRange;
[SerializeField] private List<Transform> transformList;
// 如果需要很多分区的话可以改成 SpaceUnit_2D[]
private SpaceUnit_2D partitionSpace;
public void Start()
{
OnInitialized();
}
// 如果物体数量少的时候可以直接更新全部,然后再在 partitionSpace 中统一 Move,否则要单独 transform 位置更新后Move。
public void Update()
{
OnUpdate();
}
public void OnInitialized()
{
partitionSpace = new SpaceUnit_2D(m_UltimateStack, m_UnitRange, m_MinRange,
(transform, range) => SpaceRange_2D.IsInside(transform.position, range));
foreach (Transform trans in transformList)
{
Add(trans);
}
}
// 每帧都检查是否改变位置
public void OnUpdate()
{
foreach (Transform trans in transformList)
{
partitionSpace.Move(trans);
}
}
public void Add(Transform transform)
{
if (!transformList.Contains(transform))
transformList.Add(transform);
if (partitionSpace.Add(transform))
{
DebugHelper.Message.Log("添加物品成功!");
}
else
{
DebugHelper.Message.Log("添加物品失败!");
}
}
public void OnValidate()
{
OnInitialized();
}
public void OnDrawGizmos()
{
if (partitionSpace != null)
{
// 画 Gizmos 区
}
}
}
最后,有什么不足的请大佬们在评论区分享分享观点~