Underactuated Robotics - 欠驱动机器人学（一）- 全驱动与欠驱动系统

系列文章目录

---

前言

        如今的机器人行动过于保守，只能完成机械性能所能完成的一小部分任务，实现一小部分性能。在某些情况下，我们仍然从根本上受限于在结构化工厂环境中成熟的刚性机械臂控制技术，在这种环境中，可以使用大型致动器来 "塑造 "机器的动态，以实现精度和可重复性。欠驱动机器人技术的研究重点是构建控制系统，利用机器的自然动态，力图在速度、效率或鲁棒性方面实现非凡的性能。

        在过去几年中，利用机器学习设计的控制器展示了基于优化的控制的潜在威力，但这些方法还不具备我们对更成熟的控制技术所期望的采样效率和算法可靠性。对欠驱动机器人的研究要求我们仔细观察优化机械系统时出现的优化景观，了解并在优化和学习算法中利用这种结构。

---

一、动机

让我们从一些例子和视频开始。

1.1 本田的 ASIMO 与被动式动态行走机器人的对比

        1996 年末，本田汽车公司宣布，他们已经在行走机器人技术领域闭门工作了近 15 年，自此，机器人技术的世界发生了翻天覆地的变化。他们的设计不断推陈出新，最终形成了一种被称为 ASIMO（Advanced Step in Innovative MObility）的仿人机器人。近 20 年来，本田的机器人被广泛认为代表了行走机器人的技术水平，尽管现在有许多机器人的设计和性能与 ASIMO 非常相似。我们将在讨论行走算法时，花精力了解 ASIMO 的一些细节......现在，我只想让大家熟悉 ASIMO 动作的外观和感觉 [立即观看下面的 ASIMO 视频]。

walking_while_avoiding_people

        我希望您的第一反应是对 ASIMO 动作的质量和多样性感到难以置信。现在再看一看。虽然动作非常流畅，但 ASIMO 的步态有些不自然。感觉有点像宇航员被沉重的太空服所束缚。事实上，这是一个合理的比喻... ASIMO 的行走方式有点像不熟悉自己动态的人。它的控制系统使用高增益反馈，因此需要相当大的关节扭矩，以抵消机器的自然动力，严格遵循所需的轨迹。这种控制方法带来了严重的代价。ASIMO 所消耗的能量（按比例计算）大约是人类在平地上行走所消耗能量的 20 倍（按运输成本计算）[1]。此外，这种方法中的控制稳定功能只在状态空间相对较小的部分（当站立脚平放在地面上时）起作用，因此 ASIMO 无法像人类一样快速移动，也无法在未建模或不平坦的地形上行走。

        相比之下，我们现在来看看一种截然不同的行走机器人，它被称为被动动态行走器（PDW）。这种 "机器人 "没有电机，没有控制器，也没有电脑，但仍能仅靠重力在一个小斜坡上稳定行走 [立即观看上面的视频]。大多数人都会同意，这种机器的被动步态比 ASIMO 的步态更自然，当然也更有效率。被动行走机器的历史悠久，早在 19 世纪中期就有被动行走玩具的专利。我们将详细讨论人们对这些机器动力学的了解，以及已经取得的实验成果。史蒂夫-柯林斯在康奈尔大学安迪-鲁伊纳的实验室里制造了迄今为止最令人印象深刻的被动动态行走器[2]。

robot

robot

        被动式步行器证明，在 ASIMO 上采用的高增益、动态消除反馈方法并非必要。事实上，行走的动态效果非常好，应该加以利用，而不是抵消。

        世界才刚刚开始看到这一愿景的模样。波士顿动力公司的这段视频是我最喜欢的视频之一：

        这一结果堪称工程学的奇迹（仅机械设计就令人惊叹......）。在这门课上，我们将向你传授使机器人以这种方式运行所需的计算工具。我们还将尝试推理这些类型的动作有多稳健。别担心：如果你没有一个超级轻便、超级能干、超级耐用的人形机器人，那么我们会为你提供一个模拟器。

1.2 鸟类与现代飞机

        在一种截然不同的机器上，故事却惊人地相似。现代飞机在静止的空气中进行稳定的水平飞行非常有效。螺旋桨能非常有效地产生推力，而且当今的凸面机翼已针对速度和/或效率进行了高度优化。我们很容易就会相信，我们已经没有什么可以向鸟类学习的了。但是，就像 ASIMO 一样，这些机器大多局限于非常保守的、低攻击角的飞行状态，在这种状态下，机翼上的空气动力学原理非常清楚。鸟类经常在这一飞行范围之外（例如，当它们在栖木上着陆时）执行机动动作，在利用空中能量（例如风）方面，它们比我们最好的飞机要有效得多。

        因此，鸟类是效率极高的飞行器；有些鸟类能用极少的燃料进行数千公里的迁徙。游荡的信天翁可以在不拍打翅膀的情况下飞行数小时甚至数天--这些鸟类利用风在海面上形成的剪切层，进行一种叫做动态翱翔的飞行。值得注意的是，这些鸟类飞行的代谢成本与基线代谢成本没有区别[3]，这表明它们几乎可以完全依靠风的梯度来飞行不可思议的距离（逆风或顺风）。其他鸟类通过与空气进行类似的丰富互动来提高效率，包括编队飞行、热翱翔和山脊翱翔。小型鸟类和大型昆虫，如蝴蝶和蝗虫，利用 "阵风翱翔 "主要依靠风力迁徙数百甚至数千公里。

        鸟类的机动性也令人难以置信。高度杂技飞机（如 A-4 天鹰）的滚转速率约为 720 度/秒[4]；谷仓燕的滚转速率超过 5000 度/秒[4]。蝙蝠能以全速朝一个方向飞行，并在保持前进速度的同时完全逆转方向，而这一切只需两个多拍翼，距离不到翼展的一半[5]。虽然来自机动飞行的定量流动可视化数据很少，但一种主流理论认为，这些动物产生突发性巨大机动力的能力可归因于不稳定空气动力学，例如，动物产生巨大的吸力涡旋以快速改变方向[6]。这些令人惊叹的能力经常被用于翱翔栖息、捕捉猎物以及在森林和洞穴中高速飞行等动作。即使是在高速和高转弯率的情况下，这些动物也能表现出惊人的敏捷性--蝙蝠有时会用翅膀捕捉猎物，游隼可以在以 240 英里/小时的速度俯冲时以 25 G 的速度在飞行途中抓住一只麻雀[7]，甚至可以看到我们楼外的小鸟俯冲穿过链条栅栏捕食。

        尽管已经记录了许多有关鸟类飞行的令人印象深刻的数据，但我们的理解部分受限于实验的可及性--要在不打扰鸟类的情况下仔细测量鸟类（及周围气流）最令人印象深刻的动作是相当困难的。游鱼的动态与此密切相关，也更便于研究。据了解，海豚能以 20 海里的速度在波浪中优雅地游过[6]。众所周知，蓝鳃太阳鱼等体型较小的鱼类具有一种逃逸反应，它们能在不到一个体长的时间内将自己从静止状态推进到全速状态；流动视觉效果确实证实，这是通过沿着鱼体一侧形成一个巨大的吸力漩涡来实现的[8]--这与蝙蝠在不到一个体长的时间内改变方向的方式类似。甚至还观察到死鱼通过从圆柱体的尾流中吸取能量逆流而上的现象；这种被动推进的方式可能是虹鳟在交配季节逆流而上的技术之一[9]。

1.3 机械臂

        尽管机械臂在工业应用领域取得了长期的成功，在消费应用领域也有着巨大的潜力，但我们仍然没有能够在家中执行任何有意义任务的机械臂。诚然，家用机器人的感知问题（使用传感器检测/定位物体并理解场景）非常困难。但是，即使我们拥有了完美的感知系统，我们的机器人要像人类一样灵巧、多才多艺地执行基本的物体操作任务，仍然有很长的路要走。

        如今，大多数进行物体操作的机器人都使用一种刻板的管道。首先，我们列举手部的几个接触点（这些点，也只有这些点，才允许与世界接触）。然后，给定环境中的一个局部物体，为手臂规划一条无碰撞轨迹，将手移动到 "预抓 "位置。此时，机器人会闭上眼睛（比喻）并合上手，希望预抓取位置足够好，这样就能成功抓取物体，例如，只通过手指的电流反馈就能知道何时停止合手。"动力不足的手 "使这种方法更加成功，但整个方法实际上只适用于包围式抓取。

        实际上，包络抓取方法对于一些简单的拾取和放置任务来说可能是足够的，但它并不能很好地代表人类是如何进行操纵的。当人类操纵物体时，与物体和世界的接触互动是非常丰富的--我们经常使用环境的碎片作为固定物来减少不确定性，我们通常利用滑动行为（例如拿起东西或在手中调整方向），而且如果我们使用手臂的整个表面来操纵一个大物体，我们的大脑也不会产生 NaNs。

        最近几年，计算机视觉领域的巨大进步彻底打开了这一领域。我开始将自己的研究重点放在操纵领域的问题上。在操纵领域，动态和感知之间的交互非常丰富。因此，我开设了一套完全独立的操纵笔记（和第二门课程）。

        顺便说一句，在大多数情况下，如果机器人未能在预期的接触时间/地点进行接触，就会发生糟糕的事情。结果既搞笑又令人沮丧。(让我们来解决这个问题吧！）。

1.4 共同的主题

        经典的机器人控制技术基于这样一种理念，即反馈控制可以用来控制机器的动态。与此相反，我在上面所举的例子表明，要使我们的机器人获得出色的动态性能（效率、灵活性和鲁棒性），我们需要了解如何设计控制系统来利用动态性能，而不是抵消动态性能。这就是本课程的主题。

        令人惊讶的是，机器人学中提出的许多正式控制思想并不支持 "利用 "动态的想法。最优控制公式（我们将深入研究）原则上允许这样做，但非线性系统的最优控制仍然是一个具有挑战性的问题。在我开始写这些笔记的时候，我曾开玩笑说，要说服机器人控制研究人员考虑动力学问题，你必须采取一些激烈的行动，比如剥夺她的控制权--移除电机或强制执行扭矩限制。这种有趣的系统被称为 "欠驱动 "系统。正是在 "欠驱动机器人学 "领域，开始了对我所倡导的控制类型的研究。

二、定义

        根据牛顿的观点，机械系统的动力学是二阶的（）。其状态由位置向量 q（也称为配置向量）和速度向量  以及（可能还有）时间给出。二阶控制动力系统的一般形式是： 

其中 是控制向量。

定义 1.1 （欠驱动控制微分方程）

        二阶控制微分方程描述如下：

        在状态  和时间 t 中，如果所得到的映射  是可射的：对于每一个 ，都存在一个能产生预期响应的 ，那么系统就是全驱动的。否则，就是欠驱动（状态  在时间 t）。

        正如我们将要看到的，我们所关心的许多机器人的动力学原理都是指令转矩的仿射，因此让我们来考虑一种略微受限的形式：

方程2

        对于方程描述的控制动力系统，如果我们有

        则系统在 处处于欠驱动状态。不过，这只是单向的 —— 有时我们会写出看起来像 2 的方程，并具有全秩 ，但 等附加约束也会使系统欠动。

        还请注意，我们在此使用系统一词来描述数学模型（可能是物理机器人的数学模型）。当我们说系统驱动不足时，我们指的是数学模型。试想一个带有两个执行器的双链节机器人，一个带有刚性链节的典型模型可能是完全驱动的，但如果我们增加额外的自由度来模拟链节中的少量柔性，那么这个系统模型就可能是欠驱动的。这两个模型描述的是同一个机器人，但保真度不同。两个执行器可能足以完全控制关节角度，但却无法控制关节角度和链接的弯曲模式。

        请注意，控制系统是否欠驱动可能取决于系统的状态，甚至取决于时间，不过对于大多数系统（包括本书中的所有系统）来说，欠驱动是模型的全局属性。如果一个模型在所有状态和时间下都处于欠驱动状态，我们就将其称为欠驱动模型。在实践中，只要系统在大多数状态下是完全驱动的，我们通常非正式地将其称为完全驱动系统（例如，"完全驱动 "系统可能仍然存在关节限制或在运动学奇点处失去秩）。不可否认，这允许灰色区域的存在，在灰色区域中，将模型描述为完全驱动或未完全驱动（我们应该只描述其状态）可能会让人感觉别扭；即使是工厂车间里功能强大的机械臂也有驱动器限制，但我们通常可以为它们设计控制器，就好像它们是完全驱动的一样。本文的主要关注点在于欠驱动对于制定控制策略非常有用/必要的模型。

例1.1 机械臂

简单双摆

        请看上图中的简单机器人机械手。如附录所述，该系统的运动方程非常简单，采用标准的 "机械手方程 "形式：

        众所周知，惯性矩阵 （始终）是均匀对称和正定的，因此是可逆的。将该系统转化为方程形式即可得到 

        由于  总是满秩，我们发现，如果且仅如果  是行满秩，机械手方程描述的系统就是全驱动的。在这个特殊的例子中，和 （关节处的电机扭矩）和 ，系统完全驱动。

Python 示例

        我个人认为，当我能够进行实验并获得一些物理直觉时，我的学习效果最好。这些笔记中的大多数章节都有一个可在 Deepnote 上运行的相关 Jupyter 笔记本；本章的笔记本可让您轻松查看该系统的运行情况。

        试试看！您将看到如何模拟双摆，甚至如何用符号检查动态。

 注意：您也可以在自己的机器上运行代码（详情请参见附录）。

        虽然基本的双摆锤是完全驱动的，但想象一下有点奇怪的情形：我们在肘部有一个提供扭矩的电机，但在肩部没有电机。在这种情况下，我们有  和  。这个系统显然驱动不足。虽然这听起来像是一个臆造的例子，但事实证明，它几乎就是我们将在本课稍后研究的最简单的行走模型。

        方程 2 中的矩阵 总是有 dim  行和 dim  列。因此，正如示例中的情况一样，最常见的欠动情况之一是 dim  < dim ，这就意味着  不是全行秩。当机器人的关节没有电机时，就会出现这种情况。但这并不是唯一的情况。例如，人体拥有数量惊人的致动器（肌肉），在许多情况下，每个关节拥有多块肌肉；尽管驱动器的数量多于位置变量，但当我在空中跳跃时，没有任何肌肉输入组合能改变我质心的弹道轨迹（空气动力效应除外）。我的控制系统动力不足（欠驱动）。

        关于符号的简要说明。在本课描述刚体系统动力学时，我将使用  表示构型（位置）、  表示速度，并用  表示完整状态 (  ). 附录中描述了这一约定的一个重要限制（三维角速度不应表示为三维姿态的导数），但这将使注释更加简洁。除非另有说明，矢量总是作为列矢量处理。向量和矩阵用粗体表示（标量不用粗体表示）。

三、反馈等效

        全驱动系统要比欠驱动系统更容易控制。关键的一点是，对于已知动力学的全作用系统（如  和  是已知的），可以利用反馈将任意控制问题有效地转变为控制一个微小线性系统的问题。

        如果  不是行满秩，例如每个关节有多个执行器，那么这个逆可能不是唯一的。考虑潜在的非线性反馈控制：

        其中   是新的控制输入（控制器的输入）。将此反馈控制器应用于方程  得到线性、解耦、二阶系统：

        换句话说，如果  和  是已知的，并且  是可逆的，那么我们就说该系统 "反馈等效 "于 。有许多强大的结果将这一想法推广到了  和  是估计和而非已知的情况（例如 [10]）。

例1.2 双摆的反馈消除

        比方说，我们希望我们的简单双摆能像简单单摆（带阻尼）一样运动，其动力学原理如下：

        使用以下方法即可轻松实现

        由于我们嵌入的是非线性动力学（而非线性动力学），因此我们称之为 "反馈消除 "或 "动态反转"。这个想法揭示了为什么我说控制很容易 —— 对于已知动力学的全动确定性系统这种特殊情况。例如，我本来可以很容易地反转重力。请注意，如果机器人有 100 个关节，这里的控制推导也不会更难。

        您可以在笔记本中运行这些示例：

        一如既往，我强烈建议您花几分钟时间通读源代码。

        因此，与全驱动系统不同，控制设计者别无选择，只能在控制设计中对被控对象更复杂的动态进行推理。如果这些动态是非线性的，就会使反馈控制器的设计变得非常复杂。

        一个相关的概念是反馈线性化。上例中的反馈消除控制器就是反馈线性化的一个例子 —— 利用反馈将非线性系统转换为可控线性系统。询问一个系统是否 "可反馈线性化 "并不等于询问它是否欠动；即使是可控线性系统也可能欠动，这一点我们很快就会讨论。

        也许你的背景是优化或机器学习，而不是线性控制？对于你来说，我可以说，对于全动系统，可以直接改变变量，从而使优化图（对于许多控制性能目标而言）成为凸图。这些系统的优化/学习相对容易。对于欠驱动系统，我们仍然可以利用力学来改善优化状况，但这需要更多的洞察力。开发这些洞察力是本笔记的主题之一，也将继续是一个活跃的研究领域。

四、输入和状态约束

        虽然由于缺少执行器而造成的动态限制当然体现了本课程的核心，但我们关心的许多系统也可能受到其他动态限制。例如，我们机器上的执行器可能只能产生有限的机械力矩，或者在自由空间中存在物理障碍物，我们不能允许机器人与之接触。

定义 1.2 输入和状态约束

         描述的动力系统可能受到一个或多个 描述的约束。

        在实践中，将仅取决于输入（如 ）的约束条件（如驱动器限制）分离出来可能很有用，因为它们往往比状态约束条件更容易处理。环境中的障碍物可能会表现为一个或多个仅取决于位置（如 ）的约束条件。

        根据我们对 "欠驱动 "的广义定义，我们可以看出，输入约束肯定会导致系统欠驱动。状态（仅）约束则更为微妙 —— 一般来说，这些约束实际上降低了状态空间的维度，因此需要更少维度的驱动来实现 "完全 "控制，但我们只有在能够以 "最小坐标 "进行控制设计的情况下才能从中获益（而这通常是很困难的）。

例1.3 输入限制

        考虑受约束的二阶线性系统 

        根据我们的定义，这个系统是欠驱动的。例如，没有  能产生加速度 .

        输入和状态约束会使控制设计复杂化，其方式与执行器数量不足类似（即进一步限制了可行轨迹集），通常需要类似的工具来找到控制解决方案。

4.1 非整体约束

        您可能听说过 "非全局系统"（nonholonomic system）一词（参见文献[11]），并正在思考非全局系统与欠驱动的关系。简而言之，非整体性约束是一种形式为   的约束，它无法与形式为   的约束（整体性约束）整合在一起。非整体约束并不限制系统的可能配置，而是限制达到这些配置的方式。整体约束会将系统的自由度减少一个，而非整体约束则不会。汽车或传统的轮式机器人就是一个典型的例子：

例 1.4 轮式机器人

考虑一个轮式机器人的简单模型，其配置由笛卡尔位置 和方位 来描述，因此 。 该系统受到防止侧滑的差分约束、

或等同于

        这种约束不能被整合到配置约束中 —— 汽车可以到达任何配置 ，只是不能直接侧向移动--因此这是一种非整体性约束。

        将轮式机器人与火车轨道上的机器人进行对比。火车轨道对应的是整体约束：轨道约束可以直接写成系统配置 ，而无需使用速度 。轨迹约束了系统的可能配置。

        轮式车辆上的无侧滑约束等非整体力学约束肯定会导致系统驱动不足。反之亦然--缺少驱动器的双摆系统虽然致动不足，但通常不会被称为非整体力学系统。请注意，拉格朗日运动方程的约束形式为

        因此不符合非整体约束条件。

五、欠驱动机器人技术

        如今，欠驱动系统的控制设计在很大程度上依赖于优化和最优控制，在基于模型的优化和控制的机器学习方面进展迅速，但仍有许多问题有待解决。现在正是学习这方面知识的大好时机！现在，计算机视觉已经开始发挥作用，我们可以向大型语言模型询问机器人应该做什么的高级指令（例如，"聊天 GPT，给我如何制作披萨的详细指令"），但我们在机器人学中仍有许多有趣的问题，这些问题仍然很难解决，因为它们是欠驱动的：

        足式机器人是欠驱动的。 考虑一个具有 个内部关节和 个执行器的腿式机器人。如果机器人不是用螺栓固定在地面上，那么系统的自由度既包括内部关节，也包括定义机器人在空间中的位置和方向的六个自由度。由于 n 和 n，因此满足公式 n。
(大多数）游泳和飞行机器人的驱动力不足。这里的情况与腿式机器人相同。每个控制面都会增加一个致动器和一个 DOF。这已经是一种简化，因为系统的真实状态应该包括（无限维的）流动状态。
机器人操纵（通常）是欠驱动的。考虑一个全驱动机械臂。当机械臂操纵一个具有自由度的物体时（即使一块砖头也有六个自由度），它可能会出现欠动。如果力闭合得以实现并保持，那么我们就可以认为该系统是完全致动的，因为物体的自由度受限于手的自由度。当然，除非被操纵物体具有额外的自由度（例如，任何可变形的物体）。
        即使是全驱动和无约束系统的控制系统，也可以利用欠驱动系统的经验加以改进，尤其是在需要提高运动效率或降低设计复杂度的情况下。

六、课程目标

        本课程研究优化理论、控制理论、运动规划和机器学习中快速发展的计算工具，这些工具可用于设计欠驱动系统的反馈控制。本课程的目标是开发这些工具，以便设计出比当前最先进技术更动态、更敏捷的机器人。

这门课的目标受众包括计算机科学和机械/航空专业从事机器人研究的学生。虽然我假定学生对线性代数、ODE 和 Python 比较熟悉，但课程说明旨在提供课程所需的大部分材料和参考资料。

        我得坦白一件事： 实际上，我认为我们在这些笔记中涉及的材料的价值远远超出了机器人学。我认为，系统理论为组织极其复杂系统的计算提供了一种强大的语言，尤其是当人们试图编程和/或分析反馈回路中具有连续变量的系统时（顺便说一句，这种情况在整个计算机科学和工程中都会发生）。我希望你能发现这些工具具有广泛的实用性，即使你眼前没有一个能够后空翻的仿人机器人。

七、练习

7.1 Atlas Backflip

Atlas doing a backflip and Atlas standing.

        在本章开头，您已经看到阿特拉斯人形机器人在做后空翻动作。现在请看上图中机器人的两种状态。假设 Atlas 的致动器可以产生无约束力矩 
请确定以下陈述是否为真。请简要说明理由。

• 仿人机器人的状态可以用其所有关节的角度和角速度来表示。
• 在做后空翻动作时（左图中的状态），仿人机器人完全处于活动状态。
• 站立时（右图中的状态），人形完全处于活动状态。

7.2 状态空间中的轨迹跟踪

        取一个动力学受方程 2 控制的机器人，假设它在所有时间 t 的所有状态 下都是完全驱动的。
对于任何两次可变的期望轨迹 ，是否总能找到一个控制信号 ，使 在所有 条件下都符合 和 ？
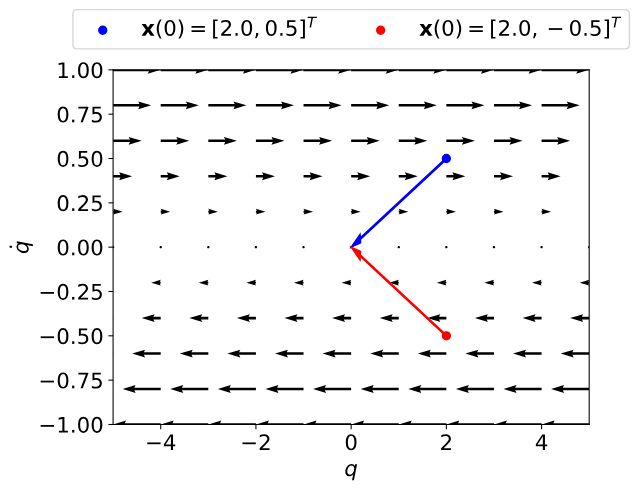
        现在来看看最简单的全驱动机器人：双积分器。这个系统的动力学方程为 ，你可以把它想象成一个质量为 的小车在直轨上移动，由力 u 控制。下图描述了当 u=0 时的相位图。是否可能找到一个控制信号 ，使双积分器从初始状态 沿直线（蓝色轨迹）到达原点？如果我们将 设为 （红色轨迹），答案会改变吗？

7.3 双摆的任务空间控制

        在上面的例子中，我们已经看到，每个关节都有一个电机的双摆是一个全驱动系统。在此，我们考虑它的一个变体：我们不使用肩部和肘部的执行器来控制机器人，而是直接对质量块 （第二连杆的顶端）施加一个力。让 成为这个力的水平分量（向右为正）和垂直分量（向上为正）。这一修改使得附录示例中推导出的运动方程几乎保持不变；唯一的区别是矩阵 现在是 的函数，即使用附录中的

        使用新控制输入的双摆是否在所有状态下都是完全驱动的？如果不是，请指出哪些状态下双摆处于欠动状态。

7.4 平面四旋翼飞行器的欠驱动

        在课程的后半部分，我们将对四旋翼飞行器的动力学进行深入研究，目前只需查看平面四旋翼飞行器部分的运动方程结构。四旋翼飞行器受限在垂直面内运动，重心向下。配置向量 包含质心位置和俯仰角。控制输入是两个旋翼产生的推力 。输入 u 可以有两种符号，并且没有限制。
        确定系统处于欠激励状态 的状态集。
        对于系统处于欠驱动的所有状态，找出一个无法瞬间达到的加速度。使用运动方程对您的主张进行严格证明：将候选加速度插入动力学中，并尝试找出矛盾之处，如 。

7.5 Drake 系统

课程软件 Drake 为动力系统提供了强大的建模语言。本笔记本中的练习将帮助您编写第一个 Drake 系统。

八、Python 示例

8.1 导入包

import matplotlib.pyplot as plt
import mpld3
import numpy as np
from IPython.display import Markdown, display
from pydrake.all import (
    AddMultibodyPlantSceneGraph,
    DiagramBuilder,
    Expression,
    LogVectorOutput,
    MakeVectorVariable,
    MeshcatVisualizer,
    MultibodyPlant,
    Parser,
    RigidTransform_,
    Simulator,
    SpatialInertia_,
    StartMeshcat,
    ToLatex,
    UnitInertia_,
    Variable,
    VectorSystem,
)

from underactuated import (
    ConfigureParser,
    ManipulatorDynamics,
    running_as_notebook,
)

if running_as_notebook:
    mpld3.enable_notebook()

# Start the visualizer (run this cell only once, each instance consumes a port)
meshcat = StartMeshcat()

 

8.2  双摆动力学

第一个单元举例说明如何运行模拟并将结果制成动画

def double_pendulum_demo():
    # Set up a block diagram with the robot (dynamics) and a visualization block.
    builder = DiagramBuilder()
    plant, scene_graph = AddMultibodyPlantSceneGraph(builder, time_step=0.0)

    # Load the double pendulum from Universal Robot Description Format
    parser = Parser(plant)
    ConfigureParser(parser)
    parser.AddModelsFromUrl(
        "package://underactuated/models/double_pendulum.urdf"
    )
    plant.Finalize()

    builder.ExportInput(plant.get_actuation_input_port())
    MeshcatVisualizer.AddToBuilder(builder, scene_graph, meshcat)
    meshcat.Set2dRenderMode(xmin=-2.8, xmax=2.8, ymin=-2.8, ymax=2.8)

    logger = LogVectorOutput(plant.get_state_output_port(), builder)

    diagram = builder.Build()

    # Set up a simulator to run this diagram
    simulator = Simulator(diagram)

    if running_as_notebook:
        simulator.set_target_realtime_rate(1.0)

    # Set the initial conditions
    context = simulator.get_mutable_context()
    context.SetContinuousState(
        [1.0, 1.0, 0.0, 0.0]
    )  # (theta1, theta2, theta1dot, theta2dot)
    diagram.get_input_port(0).FixValue(
        context, [0.0, 0.0]
    )  # Zero input torques

    # Simulate
    simulator.AdvanceTo(10.0)

    # Plot the results
    plt.figure()
    fields = ["shoulder", "elbow"]
    log = logger.FindLog(context)
    for i in range(2):
        plt.subplot(2, 1, i + 1)
        plt.plot(log.sample_times(), log.data()[(i, i + 2), :].transpose())
        plt.legend(["position", "velocity"])
        plt.xlabel("t")
        plt.ylabel(fields[i])
        plt.grid(True)
    display(mpld3.display())


double_pendulum_demo()

值得一看的是描述机器人的文件。URDF 和 SDF 是两种标准格式，它们甚至可以用来描述非常复杂的机器人（如波士顿动力公司的仿人机器人）。

  
    
  
  
    
  

  
    
      
      
      
    
  
  
    
    
  

  
     
      
      
       
    
    
      
      
         
      
      
     
    
      
      
        
      
      
    
  
  
    
    
    
  
  
    
    
    1
  

  
     
      
      
       
    
    
      
      
         
      
      
     
    
      
      
        
      
      
    
  
  
    
    
    
    
  
  
    
    
    1
  

8.3 检查动力学（机械手方程）

我们还可以使用 Drake 来评估操纵器方程。 首先，我们将评估特定机器人（为质量、链路长度等分配数值）和特定机器人状态下的操纵器方程。

plant = MultibodyPlant(time_step=0)
parser = Parser(plant)
ConfigureParser(parser)
parser.AddModelsFromUrl("package://underactuated/models/double_pendulum.urdf")
plant.Finalize()

# Evaluate the dynamics numerically
q = [0.1, 0.1]
v = [1, 1]
(M, Cv, tauG, B, tauExt) = ManipulatorDynamics(plant, q, v)
display(Markdown("$M = " + ToLatex(M, precision=2) + "$"))
display(Markdown("$Cv = " + ToLatex(Cv, precision=2) + "$"))
display(Markdown("$\\tau_G = " + ToLatex(tauG, precision=2) + "$"))
display(Markdown("$B = " + ToLatex(B, precision=2) + "$"))
display(Markdown("$\\tau_{ext} = " + ToLatex(tauExt, precision=2) + "$"))

Drake 在支持符号计算（使用浮点系数）方面也相当独特。 下面是一个打印双摆符号动力学的例子。 (如果你曾经写出过机器人的方程式，你就会知道它们很快就会变得复杂！）。 

# Evaluate the dynamics symbolically
def SymbolicManipulatorEquations():
    plant = MultibodyPlant(time_step=0)
    parser = Parser(plant)
    ConfigureParser(parser)
    parser.AddModelsFromUrl(
        "package://underactuated/models/double_pendulum.urdf"
    )
    plant.Finalize()

    sym_plant = plant.ToSymbolic()
    sym_context = sym_plant.CreateDefaultContext()

    # State variables
    q = MakeVectorVariable(2, "q")
    v = MakeVectorVariable(2, "v")
    vd = MakeVectorVariable(2, "\dot{v}")

    # Parameters
    m = MakeVectorVariable(2, "m")
    l = MakeVectorVariable(2, "l")

    # TODO: pending https://github.com/RobotLocomotion/drake/issues/17245
    # g = Variable("g")
    # sym_plant.mutable_gravity_field().SetGravityVector(sym_context, [0, 0, -g])

    upper_arm = sym_plant.GetBodyByName("upper_arm")
    inertia = SpatialInertia_[Expression](
        m[0],
        [0, 0, -l[0]],
        UnitInertia_[Expression](l[0] * l[0], l[0] * l[0], 0),
    )
    upper_arm.SetSpatialInertiaInBodyFrame(sym_context, inertia)
    lower_arm = sym_plant.GetBodyByName("lower_arm")
    inertia = SpatialInertia_[Expression](
        m[1],
        [0, 0, -l[1]],
        UnitInertia_[Expression](l[1] * l[1], l[1] * l[1], 0),
    )
    lower_arm.SetSpatialInertiaInBodyFrame(sym_context, inertia)
    elbow_frame = sym_plant.GetJointByName("elbow").frame_on_parent()
    elbow_frame.SetPoseInParentFrame(
        sym_context, RigidTransform_[Expression]([0, 0, -l[0]])
    )
    (M, Cv, tauG, B, tauExt) = ManipulatorDynamics(
        sym_plant, q, v, sym_context
    )
    display(Markdown("$M = " + ToLatex(M, precision=2) + "$"))
    display(Markdown("$Cv = " + ToLatex(Cv, precision=2) + "$"))
    display(Markdown("$\\tau_G = " + ToLatex(tauG, precision=2) + "$"))
    display(Markdown("$B = " + ToLatex(B, precision=2) + "$"))
    display(Markdown("$\\tau_{ext} = " + ToLatex(tauExt, precision=2) + "$"))


SymbolicManipulatorEquations()

我们使用类似的机制来支持自动区分；我们很快就会看到这方面的例子！ 

8.4 双摆的反馈消除 

像单摆一样行动
首先，我们将简单控制器作为一个系统来实现，该系统接收摆锤状态并输出电机扭矩。 

class Controller(VectorSystem):
    """Defines a feedback controller for the double pendulum.

    The controller applies torques at the joints in order to:

    1) cancel out the dynamics of the double pendulum,
    2) make the first joint swing with the dynamics of a single pendulum, and
    3) drive the second joint towards zero.

    The magnitude of gravity for the imposed single pendulum dynamics is taken
    as a constructor argument.  So you can do fun things like pretending that
    gravity is zero, or even inverting gravity!
    """

    def __init__(self, multibody_plant, gravity):
        # 4 inputs (double pend state), 2 torque outputs.
        VectorSystem.__init__(self, 4, 2)
        self.plant = multibody_plant
        self.g = gravity

    def DoCalcVectorOutput(self, context, double_pend_state, unused, torque):
        # Extract manipulator dynamics.
        q = double_pend_state[:2]
        v = double_pend_state[-2:]
        (M, Cv, tauG, B, tauExt) = ManipulatorDynamics(self.plant, q, v)

        # Desired pendulum parameters.
        length = 2.0
        b = 0.1

        # Control gains for stabilizing the second joint.
        kp = 1
        kd = 0.1

        # Cancel double pend dynamics and inject single pend dynamics.
        torque[:] = (
            Cv
            - tauG
            - tauExt
            + M.dot(
                [
                    self.g / length * np.sin(q[0]) - b * v[0],
                    -kp * q[1] - kd * v[1],
                ]
            )
        )


def simulate(gravity=-9.8):
    builder = DiagramBuilder()
    plant, scene_graph = AddMultibodyPlantSceneGraph(builder, time_step=0.0)

    # Load the double pendulum from Universal Robot Description Format
    parser = Parser(plant)
    ConfigureParser(parser)
    parser.AddModelsFromUrl(
        "package://underactuated/models/double_pendulum.urdf"
    )
    plant.Finalize()

    controller = builder.AddSystem(Controller(plant, gravity))
    builder.Connect(
        plant.get_state_output_port(), controller.get_input_port(0)
    )
    builder.Connect(
        controller.get_output_port(0), plant.get_actuation_input_port()
    )

    MeshcatVisualizer.AddToBuilder(builder, scene_graph, meshcat)
    meshcat.Set2dRenderMode(xmin=-2.8, xmax=2.8, ymin=-2.8, ymax=2.8)

    diagram = builder.Build()

    # Set up a simulator to run this diagram
    simulator = Simulator(diagram)
    if running_as_notebook:
        simulator.set_target_realtime_rate(1.0)

    # Set the initial conditions
    context = simulator.get_mutable_context()
    context.SetContinuousState((1.0, 0.0, 0.2, 0.0))  # (θ₁, θ₂, θ̇₁, θ̇₂)

    # Simulate
    simulator.AdvanceTo(3.0)

如果我们用默认参数（重力 = -9.8m/s）来模拟这个系统，那么我们的双摆就会像单摆一样。

simulate()

 但是，如果我们已经走到了这一步，我们几乎可以用任何东西来取代动力学。 例如，只需一个简单的改动，我们就能利用反馈消除来反转重力！

simulate(gravity=9.8)

References

1. Steven H. Collins and Andy Ruina and Russ Tedrake and Martijn Wisse, "Efficient bipedal robots based on passive-dynamic walkers", Science, vol. 307, pp. 1082-1085, February 18, 2005. [ link ]
2. Steven H. Collins and Martijn Wisse and Andy Ruina, "A Three-Dimensional Passive-Dynamic Walking Robot with Two Legs and Knees", International Journal of Robotics Research, vol. 20, no. 7, pp. 607-615, July, 2001.
3. J.P.Y. Arnould and D.R. Briggs and J.P. Croxall and P.A. Prince and A.G. Wood, "The foraging behaviour and energetics of wandering albatrosses brooding chicks", Antarctic Science, vol. 8, no. 3, pp. 229-236, 1996.
4. Wei Shyy and Yongsheng Lian and Jian Teng and Dragos Viieru and Hao Liu, "Aerodynamics of Low Reynolds Number Flyers", Cambridge University Press , 2008.
5. Xiaodong Tian and Jose Iriarte-Diaz and Kevin Middleton and Ricardo Galvao and Emily Israeli and Abigail Roemer and Allyce Sullivan and Arnold Song and Sharon Swartz and Kenneth Breuer, "Direct measurements of the kinematics and dynamics of bat flight", Bioinspiration \& Biomimetics, vol. 1, pp. S10-S18, 2006.
6. Michael S. Triantafyllou and George S. Triantafyllou, "An efficient swimming machine", Scientific American, vol. 272, no. 3, pp. 64, March, 1995.
7. Vance A. Tucker, "Gliding Flight: Speed and Acceleration of Ideal Falcons During Diving and Pull Out", Journal of Experimental Biology, vol. 201, pp. 403-414, Nov, 1998.
8. Eric D. Tytell and George V. Lauder, "Hydrodynamics of the escape response in bluegill sunfish, Lepomis macrochirus", The Journal of Experimental Biology, vol. 211, pp. 3359-3369, 2008.
9. D.N. Beal and F.S. Hover and M.S. Triantafyllou and J.C. Liao and G. V. Lauder, "Passive propulsion in vortex wakes", Journal of Fluid Mechanics, vol. 549, pp. 385芒鈧€�402, 2006.
10. Jean-Jacques E. Slotine and Weiping Li, "Applied Nonlinear Control", Prentice Hall , October, 1990.
11. Anthony Bloch and P. Crouch and J. Baillieul and J. Marsden, "Nonholonomic Mechanics and Control", Springer , April 8, 2003.

注：这是麻省理工学院一门课程的工作笔记。它们将在 2023 年春季学期中不断更新。

@book{underactuated,
  title        = "Underactuated Robotics",
  subtitle     = "Algorithms for Walking, Running, Swimming, Flying, and Manipulation",
  howpublished = "Course Notes for MIT 6.832",
  author       = "Tedrake, Russ",
  year         = 2023
}