王道考研计算机组成原理——数据的表示和运算
数制转换
任意进制》十进制:位权*位数即可
整数部分补0是补在头部,小数部分补0是补在尾部
一般都是先把十进制》二进制;然后二进制再转换成8/16进制这样子
一种更快的方法->拼凑法:小数部分整数部分都可以这样求
一般都是先把十进制》二进制;然后二进制再转换成8/16进制这样子
正负号需要被数字化:需要被转换成0/1
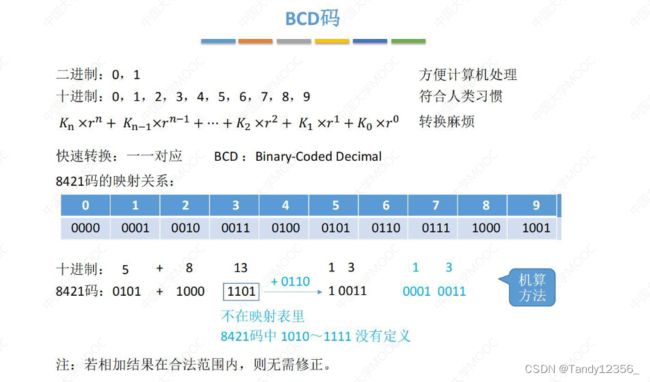
BCD码
BCD8421码:如果两个数相加落到了一个非法区间内(1010-10010),就加上6进行修正
8421指的是每一位的权重
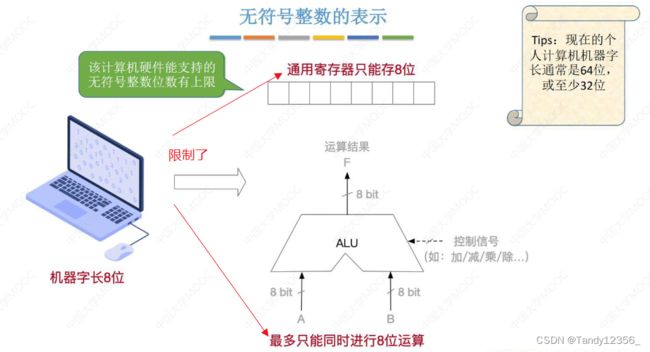
无符号整数
机器字长:计算机进行一次整数运算所能处理的二进制数据的位数,也就是计算机的位数
 一个二进制数取反后和原来的数相加结果就是全1,再加1就是每位全0对应的是相反数的代数和是0
一个二进制数取反后和原来的数相加结果就是全1,再加1就是每位全0对应的是相反数的代数和是0
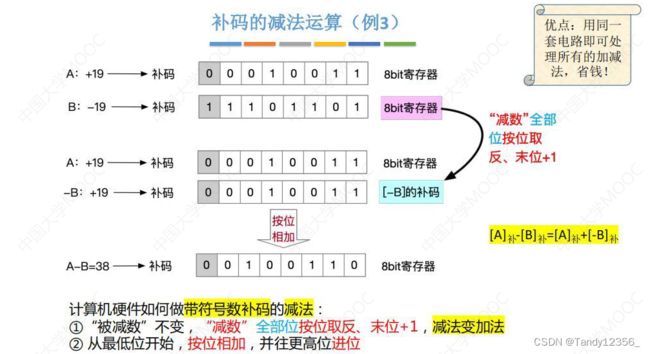
减去一个数等于加上这个数的负数,即反码加一
减法》加上负数(注意位数一定要对齐!!!)
有符号整数
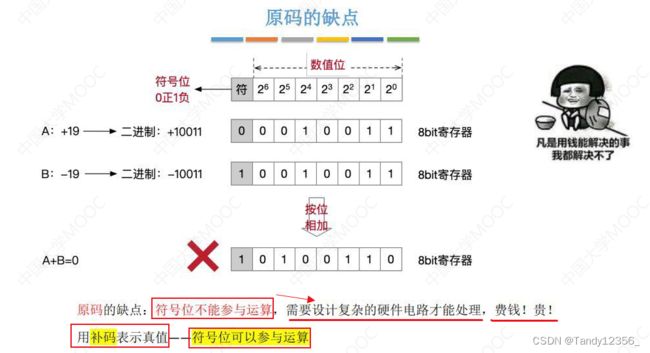
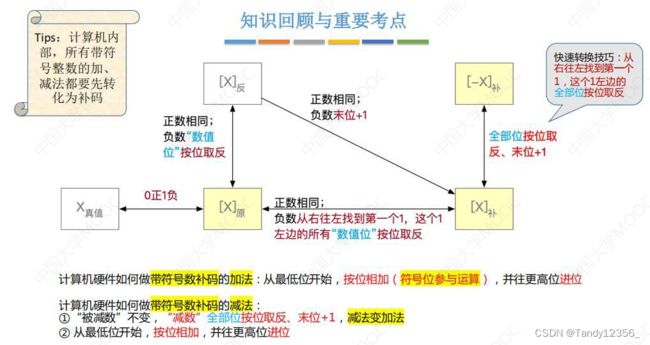
原码、反码、补码
计算机内部的数都是使用补码存储,但是原码》补码需要先转换成反码
原码》反码:正数、负数
符号位不变,其余位按位取反
补码》反码:反码》原码》反码
原码《》补码快速转换的方法:
使用补码之后,所有的比特位都用同样的规则去处理,这是计算机非常喜欢做的事
补码的数值位就不能解读为权值了
有符号数补码的加法直接相加就行,得到的当然也是补码了
引入补码最根本的原因:符号位也可以参与运算
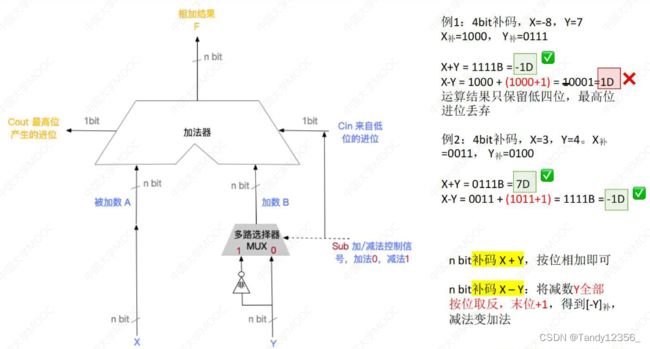
补码的加减运算
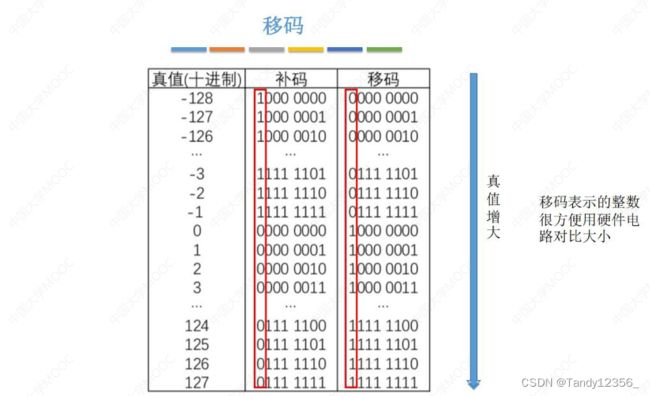
移码
答案:
定点小数的计算
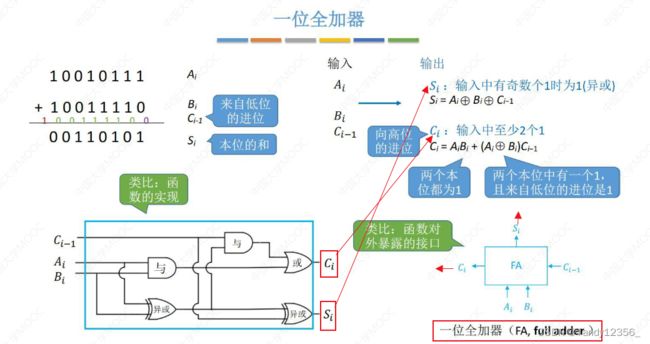
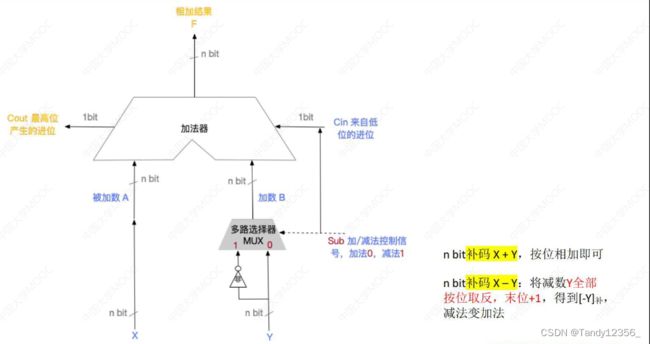
加法器
M=1表示这是一个逻辑运算,M=0表示这是一个算术运算
机器字长的本质就是ALU同时支持输入多少bit的信息,然后据此设置各个寄存器的长度
加法器的设计
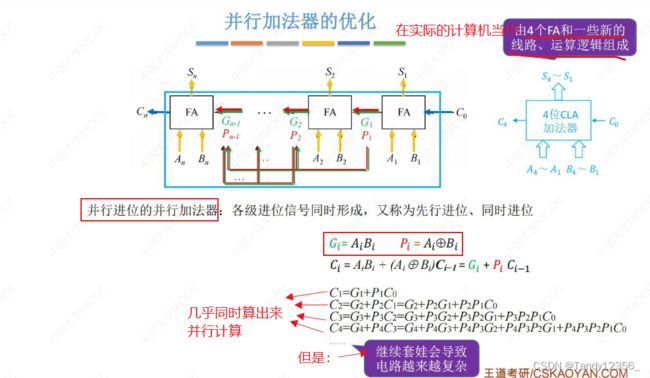
并行加法器的优化
只有两个符号相同的数相加的时候才会发生溢出
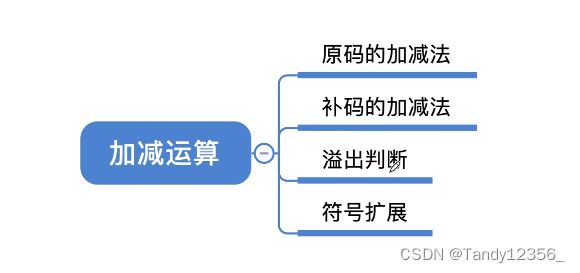
有符号数的加减法运算
溢出判断
方法三:双符号位补码
上溢:整数超过上限,下溢:负数超过下限
![]()
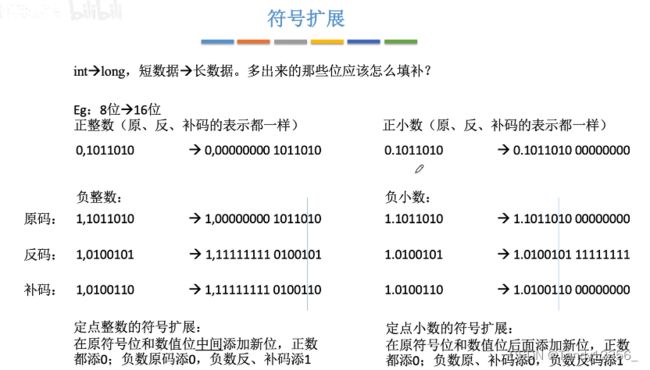
定点小数的符号扩展问题:
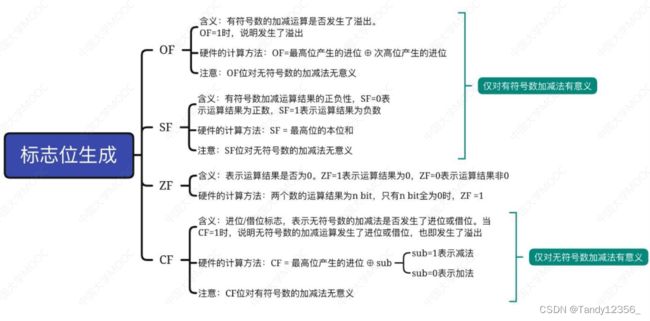
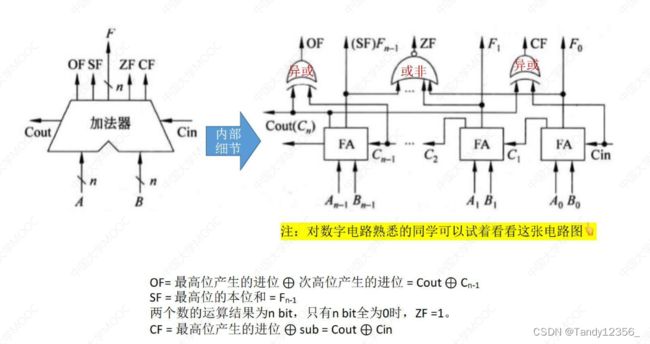
标志位的生成
无论是有符号数的加减运算还是无符号数的加减运算,在底层都是用同一套电路来实现的
无符号数加减运算使得OF=1也是没有意义的
OF=最高位产生的进位 异或 次高位产生的进位
重点是OF SF ZF
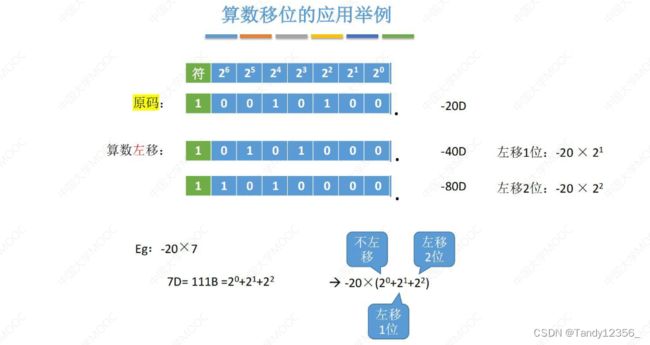
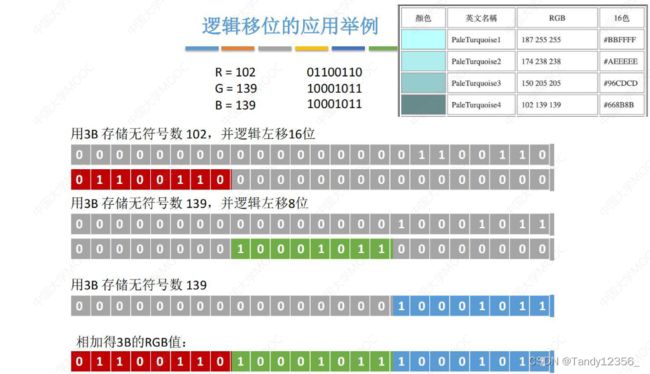
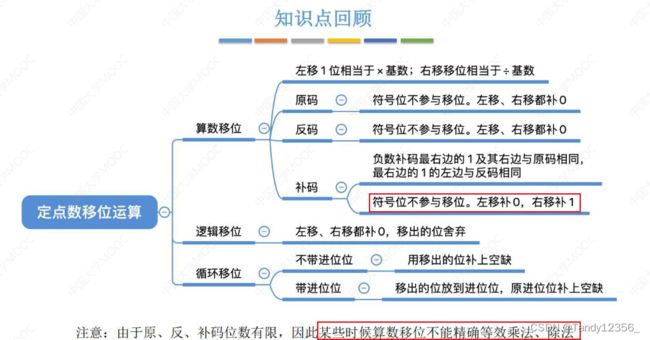
各种移位操作
![]()
符号位不变,数值位进行移位
原码的移位:左移(低位补0,高位舍去)右移:(低位舍弃,高位补0)
补码的移位:
正数的补码:和原码一样,左右移都补0
负数的补码:左移补0,右移补1
逻辑移位不管左移右移都是补0,而算术移位需要具体看符号位
所以为啥不直接mov?
循环移位:n次移位
带进位位也是一样,CF也要参与循环移位
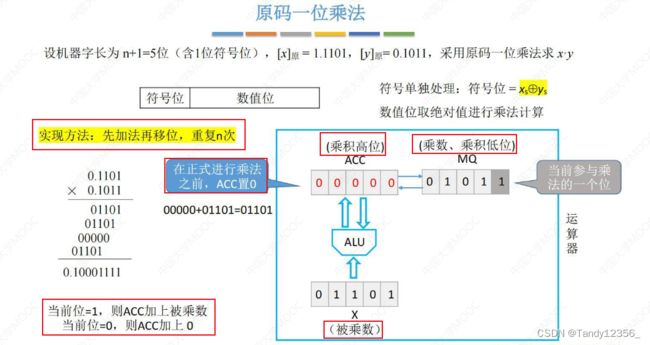
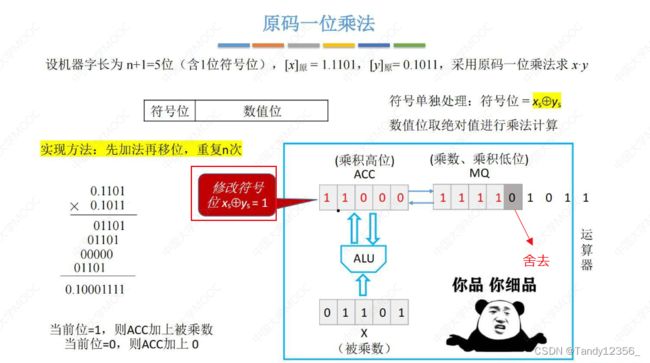
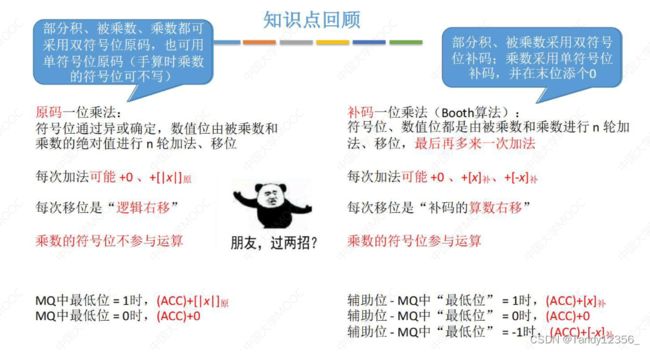
定点数原码乘法运算
被乘数X固定,每次都是同一个
MQ的最后一位就是本次参与乘法的一位
先加法再移位,重复n次,ACC是逻辑右移,移动之后,最低位移动到MQ当中
每次加法之后一定要先移位
整数的乘法也和小数的乘法是类似的
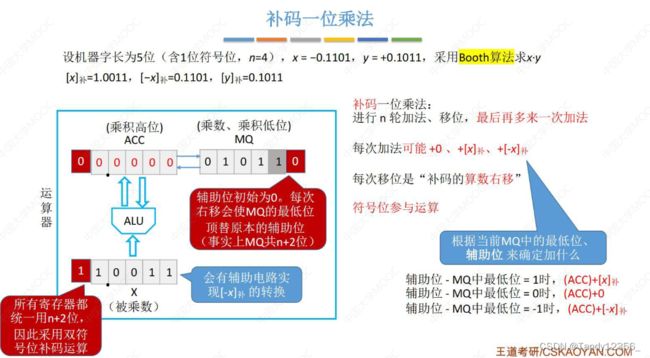
定点数补码乘法运算
补码的乘法是算术右移,而原码是逻辑右移
MQ真正的最低位是辅助位,辅助位是多出来的一位,我们为了和前面统一,最低位
由于MQ当中多了一位辅助位,为了使CPU寄存器的位数保持一致,其他寄存器采用双符号位补码运算
原码的乘法运算MQ和X寄存器当中存放的是乘数和被乘数的绝对值,而在补码乘法当中直接把完整的补码给存进来了(包含符号位)
被乘数是双符号位的补码,乘数是单符号位的补码
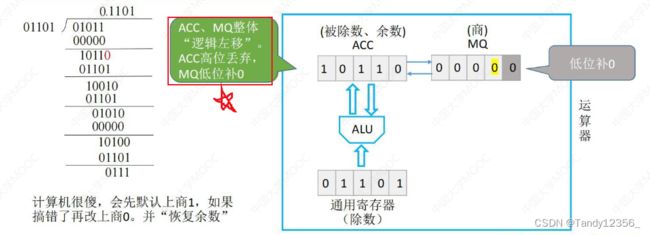
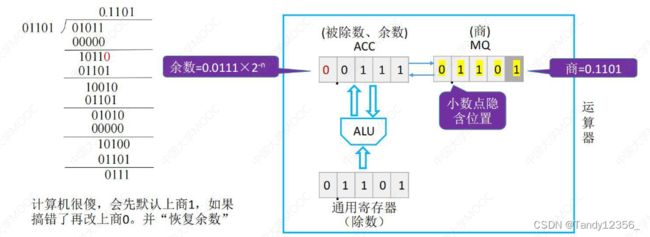
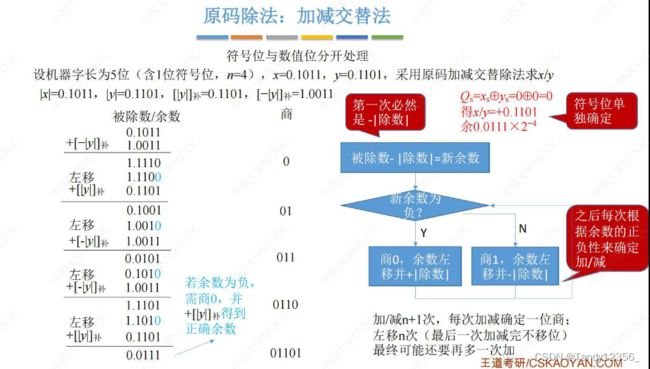
定点数原码除法运算
定点小数无法表示大于1的小数
建议手算模拟一遍左边红框内容:
果然搞错了。。。:
最终结果:
实现思路:
定点数补码除法运算
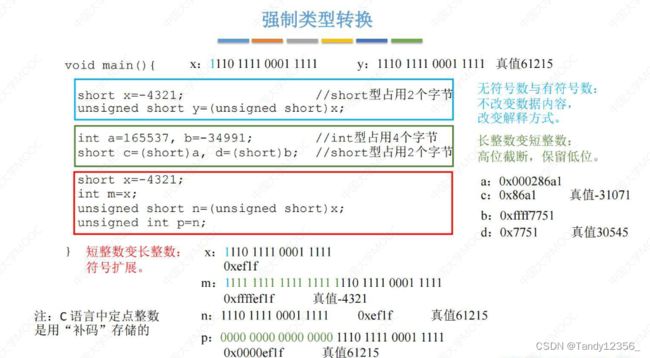
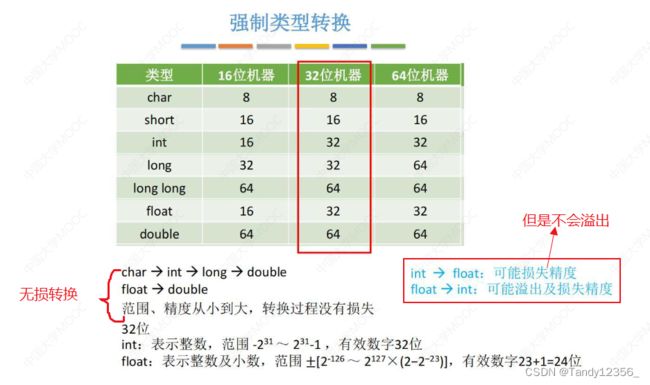
C语言中的强制数据类型转换
注:计算机底层所有的定点整数都是使用补码存储
无符号数《》有符号数:不改变数据内容,只改变解释方式
长整数int变成短整数short:直接高位截肢,只保留低位
短整数变长整数:符号扩展
①有符号数0xef1f:符号位全补1(是0是1根据具体情况而定)
②无符号数0xef1f:符号位全补0
大端小端模式
小端模式便于机器阅读(机器也是从低地址往高地址读取的),比如只需要读入1个字节,直接读低地址的67H它不香吗?
使用小端存储的方式,计算机首先从内存里读入的,就是最初、最应该先被处理的字节,所以小端存储的方式会更便于计算机处理
符合人类直觉的12345678就是大端模式
最后都要转换成按字节寻址(逻辑左移)
比如:int*p=MyStuct;p++;
最终p++的实现需要p+(1<4)
这里有歧义,word是2个字节,dword才是四字节吧?
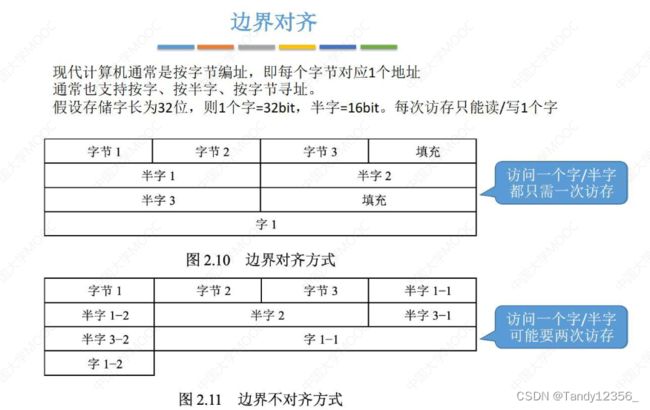
按照4字节对齐,每次操作都只需要一次访存!!!如果不按照4字节对齐的话,word和dword可能面临两次访存的额外开销!所以计算机设计时一般考虑空间换时间
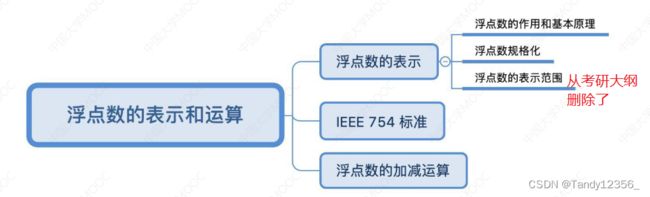
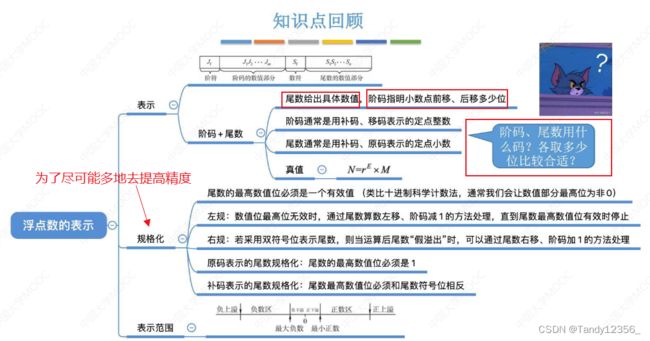
浮点数的表示
long:八字节的定点整数
定点数的局限性:
a:
b的尾数多了一位,只能舍弃,导致丢失精度
那么如何在存储空间一定的情况下(比如都是1B)尽可能地去保留它的精度呢?
对于b来说第一个位是符号位必须保留,而小数点后面的0是无效值可以丢弃
算术左移,阶码-1(010->001);数字右移相当于小数点左移,所以阶码得减去移动的位数
浮点数的规格化
当浮点数运算的结果尾数出现溢出的时候(双符号位位01/10),使用双符号位可以纠正这次溢出
规格化:科学计数
![]()
规格化之后的浮点数的特点:
最大正数:2^1+2^2+...+2^n=1-2e-n 》0.111111...
最小正数:1/2 》0.100000...
负数:直接对不等号取反即可
补码的形式:便于计算机硬件判断这个浮点数是否已经被规格化
规格化后:0.011;1.0100000
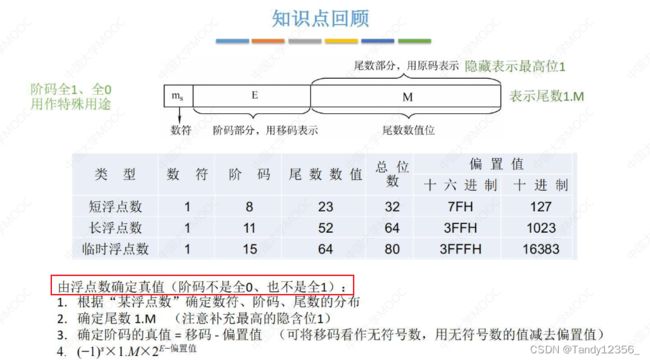
IEEE754标准
由于寄存器只有8位,所以mod 2^8不影响
0放在正数那里,所以是-128-127,其中-128和-127用作别的功能
偏置值:2^(E-1)-1=127/1023
阶码真值计算的时候,可以使用移码和偏移量的真值相减
阶码=真值+偏置值
IEEE:移码=阶码真值+偏移量
一律先规格化!!!
移码可以直接看作无符号数
浮点数的运算
小阶向大阶对齐是为了方便计算机对尾数进行处理
阶码的溢出才是真正的溢出,尾数的溢出是假溢出,因为还可以通过双符号位的规格化来纠正
-Y的补码:包括符号位在内,按位取反再+1
根据双符号位的最高位
因为尾数保留的是定点小数,所以要把尾数转换成0.XXX
各种数据类型转换
g无损转换
float》int:只保留整数部分,小数部分全部砍掉,所以会损失精度