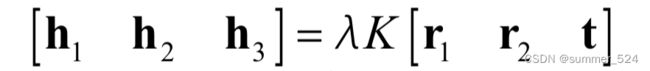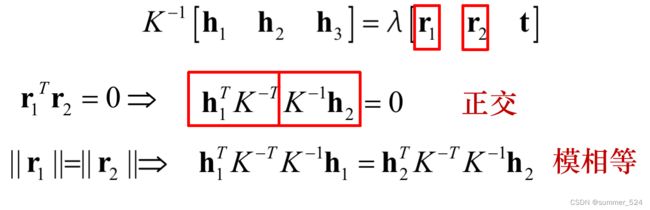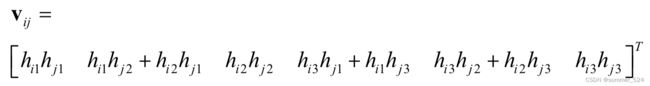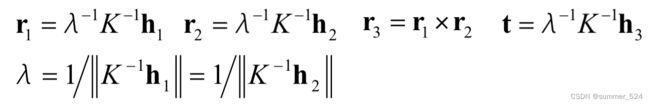Python计算机视觉（四）—照相机标定

1. 照相机标定原理

    照相机标定的目的是获得照相机自身的参数，合适的标定参数是照相机准确获得目标信息的先决条件。本文向大家介绍张正友相机标定法。相机标定的过程是将世界坐标系通过刚体变换转换为相机坐标系，接着通过投影变换将相机坐标系转换为图像坐标系，最后再将图像坐标系通过平移变换转换到像素坐标系。相机拍摄过程中的坐标系转换关系如下图所示。

坐标系转换关系图

 2. 张正友相机标定法

    张正友标定是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。此方法介于传统标定法和自标定法之间，既克服了传统标定法需要的高精度标定物的缺点，同时相较于自标定法提高了精度，便于操作。因此张正友标定法被广泛应用于计算机视觉方面。

张正友标定法一般步骤：

1.打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上

2.针对棋盘格拍摄若干张图片（一般10-20张）

3.在图片中检测特征点（Harris角点）

4.根据角点位置信息及图像中的坐标，求解Homographic矩阵

5.利用解析解估算方法计算出5个内部参数，以及6个外部参数

6.根据极大似然估计策略，设计优化目标并实现参数的refinement

3. 张正友标定法数学原理

3.1 参数介绍

2D 图像点：

3D 空间点:

齐次坐标:,

描述空间坐标到图像坐标的映射:

s: 世界坐标系到图像坐标系的尺度因子

K: 相机内参矩阵

:外参矩阵

: 像主点坐标

α, β: 焦距与像素横纵比的融合

γ: 径向畸变参数 

3.2 内参求解

不妨设棋盘格位于Z = 0 ，

定义旋转矩阵R的第i列为 ， 则有：

于是空间到图像的映射可改为：

     

其中H 是描述Homographic矩阵,可通过最小二乘从角点世界坐标到图像坐标的关系求解

令 H 为 H = [h1 h2 h3]

Homography 有 8 个自由度， 通过上述等式的矩阵运算，根据r1和r2正交，以及归一化的约束可以得到如下等式：

定义 = =

 B 是对称阵，其未知量可表示为6D 向量 

设H中的第i列为 ， 根据b的定义，推导出:

可推导出：

如果有n组观察图像，则V 是 2n x 6 的矩阵 Vb=0，

根据最小二乘定义，V b = 0 的解是 最小特征值对应的特征向量，

因此, 可以直接估算出 b，后续可以通过b求解内参。

当观测图像 n ≥ 3 时，可以得到b的唯一解 ；当 n = 2时, 一般可令畸变参数γ = 0； 当 n = 1时, 仅能估算出α 与 β, 此时一般可假定像主点坐标 与为0。

，B 是通过b构造的对称矩阵，

内部参数可通过如下公式计算(cholesky分解)：

 3.3 外参求解

外部参数可通过Homography求解，，可推导出：

 一般而言，求解出的不会满足正交与归一的标准， 在实际操作中，R 可以通过SVD分解实现规范化。

4. 实验过程

1.准备一张5X5的黑白棋盘格如下图所示

2.调整摄像机角度拍摄不同方向的棋盘格照片，图像集如下图所示

 3.提取图像中棋盘格角点，角点图像集如下图所示

示例如下图所示：

​​​​​​​

 

4.代码

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差阈值0.001
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 35, 0.001)

# 获取标定板4*4角点的位置
objp = np.zeros((4*4,3), np.float32)
objp[:,:2] = np.mgrid[0:4,0:4].T.reshape(-1,2) # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = [] # 存储3D点
img_points = [] # 存储2D点

# 获取指定目录下.jpg图像的路径
images = glob.glob(r"/Users/xionglulu/Downloads/project1/BW/*.jpg")
# print(images)

i=0
for fname in images:
    # print(fname)
    img = cv2.imread(fname)
    # 图像灰度化
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    # 获取图像角点
    ret, corners = cv2.findChessboardCorners(gray, (4, 4), None)
    # print(corners)

    if ret:
        # 存储三维角点坐标
        obj_points.append(objp)
        # 在原角点的基础上寻找亚像素角点，并存储二维角点坐标
        corners2 = cv2.cornerSubPix(gray, corners, (1, 1), (-1, -1), criteria)
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)
        # 在黑白棋盘格图像上绘制检测到的角点
        cv2.drawChessboardCorners(img, (4, 4),corners, ret)
        i+=1
        cv2.imwrite('conimg'+str(i)+'.jpg', img)
        cv2.waitKey(10)
print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print('------照相机内参与外参------')
print("ret:", ret) # 标定误差
print("mtx:\n", mtx) # 内参矩阵
print("dist:\n", dist) # 畸变参数 distortion coefficients = (k_1,k_2,p_1,p_2,k_3)
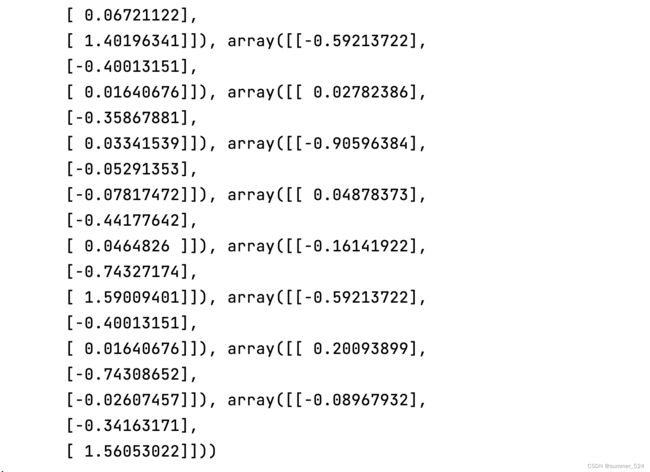
print("rvecs:\n", rvecs) # 旋转向量 # 外参数
print("tvecs:\n", tvecs ) # 平移向量 # 外参数


img = cv2.imread(images[10])
print(images[10])
h, w = img.shape[:2]
# 计算一个新的相机内参矩阵和感兴趣区域（ROI）
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
print('------新内参------')
print (newcameramtx)
print('------畸变矫正后的图像newimg.jpg------')
newimg = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
newimg = newimg[y:y+h,x:x+w]
cv2.imwrite('newimg.jpg', newimg)
print ("newimg的大小为:", newimg.shape)

 5.实验结果

原图像

畸变矫正后的图像

 6. 实验结果分析

（1）ret：标定的误差，表示重投影误差的平均值或总和。重投影误差是指将标定结果应用于棋盘格图像时，通过将三维坐标投影到二维平面上，计算预测的像素坐标与实际像素坐标之间的误差。重投影误差越小，表示标定结果越准确。本次实验标定误差为3.3357，这个误差还是挺大的，可能是图像数量少或者拍摄角度倾斜较大导致的。

（2）从实验结果中可以看出，内参矩阵mtx中参数像素间距的值为0，表明相机的像素间距是均匀的，这种情况下，相邻像素在图像平面上的间距是相等的。

（3）观察原图像和畸变矫正处理后的图像几乎没有区别，可能是标定数据不足或标定板精度较低：如果标定数据不足或标定板精度较低，则会影响标定的精度和准确性，从而导致畸变矫正效果不佳；或者相机成像畸变较小：如果相机成像时的畸变较小，则畸变矫正处理后的图像与原始图像差别不大。