PyTorch | 快速入门教程

01 | 写在前面

PyTorch作为日益受到学术界喜爱的一种深度学习实现框架，对应的各种技术书籍也如雨后春笋般涌入视线。然而由于PyTorch自身具有强大的功能实现和灵活的自定义控制，若想短时间内吃透也并非易事。

PyTorch最好的学习方式之一莫过于边学边实践，一层含义是利用实时交互反馈的代码效果，立竿见影般将模块、方法功能与使用规范映入脑中；另一层含义则是遵循认知过程中循环上升模式，先建立对PyTorch基本功能的认知，然后在后续技术实践中逐步扩充、完善、加深对PyTorch技术框架的理解掌握。

基于上述认识，本篇笔记整理了学习PyTorch时应知应会的模块、方法，帮助大家快速上手入门。

02 | PyTorch的数据结构：张量

张量的本质可以看作数据在不同方向上延展得到的多维数组，与Python中列表对象不同，PyTorch将张量对象的数据顺序存储在连续内存块中。张量是PyTorch操作的主要数据结构，尤其是ANN中输入、各层模型参数以及输出均以张量的形式展现处理，因此学习PyTorch必须首先理解掌握张量的基础操作。

021 | 初始化（创建）张量

操作张量的前提是：我们得先有一个张量。

PyTorch中提供了下述实用的张量初始化方法：

• 采用torch.rand()或torch.randn()随机初始化指定形状的张量，括号内输入张量大小（即形状，如3×3）
• 采用torch.zeros()或torch.ones()快速初始化指定形状的张量，其元素数值全为0或1
• 采用torch.tensor()方法从既有的列表对象中镜像一个张量，张量的元素数值与形状均与列表相同

尝试在Jupyter中输入下述代码，其中使用.size()方法查看张量的形状（大小）：

# 张量初始化方法

```php
x = torch.rand(5, 3)    # 随机初始化一个5×3大小的张量
y = torch.ones(5, 3, dtype=torch.double)
z = torch.tensor([5, 3.0])
d = torch.tensor(1.0)
print("张量初始化方法：")
print(x, x.size())
print(y, y.size())
print(z, z.size())
print(d, d.size())

022 | 张量的运算

PyTorch支持对张量进行运算，如张量间的加法或乘法。当张量与张量运算时，效果等同于张量对应位置元素运算；当张量与标量运算时，效果等同于张量所有元素均与该标量运算。

尝试在Jupyter中输入下述代码。张量相加可以直接使用“+”也可以采用张量自带方法y.add_(x)。

注意：通常张量运算的结果是创建一个新张量接受运算输出，若想直接对原张量产生变化，则需采用“in-place”操作，即选择添加了“”的方法版本，如.add()而非.add()。

# 张量的加法
x_1 = torch.tensor([[1, 2], [3, 4]])
y_1 = torch.ones(2, 2)
print('\n\n张量的加法运算：')
print(x_1, y_1)
print(x_1 + y_1)
result = torch.zeros(2, 2)
print(torch.add(x_1, y_1, out=result))  
# 可以使用参数out=指定张量 

# 张量的乘法
x_2 = torch.tensor(range(4)).view(2,2)
y_2 = torch.tensor([[1,2], [1,2]])
print("张量的乘法：")
print("x_2 is", x_2)
print("y_2 is", y_2)
z_2 = x_2 * y_2
print("z_2 is", z_2)

023 | 张量的查看

PyTorch中的张量完美兼容Numpy中的数据分片机制，因此可以采用类似的形式[a:b, c:d]查看特定位置的张量元素。

如在Jupyter中输入下述代码，查看张量中第二列元素：

# 张量兼容Numpy中的索引分片
print("张量的索引分片：")
print(x)
print(x[:, 1])  # 输出张量x的第一行到最后一行的编号为1的列

另一方面，PyTorch中的张量元素顺序存储在连续内存块中，因而只要数据本身不变，可以选择不同的“视图”筛选元素。PyTorch中提供了.view()方法来投影指定形状的张量视图，其中“-1”表示该方向的维度数量由其他确定的方向维度计算得到。

如对于一个2×8大小的张量，当选择.view(-1,16)时，显然实际得到的是（1,16）形状的张量。

# 张量的视图变换
# 内存中存储不变，仅仅改变投影方式
# torch.randn:用来生成随机数字的tensor，这些随机数字满足标准正态分布（0~1）
# 参数可以是单个整数，也可以是一个元祖表示大小（形状）
x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8)   
# "-1"表示该维度大小由其他维度大小推得print("\n\n张量的view操作：")print(x, x.size())print(y, y.size())print(z, z.size())

03 | PyTorch的自动微分机制

PyTorch的强大之处表现在具有自动微分机制。通过在模型定义组建阶段建构计算图，从而可以在执行.backward()方法时自动计算自变量（默认为仅保存图中的叶子节点）的梯度数值。

当然，计算梯度意味着额外的计算资源与消耗，因而PyTorch并非对所有张量保存梯度，当我们需要查看某个张量的梯度时，需要指定“requires_grad=True”。

如果我们需要查看某个非叶子节点的梯度（grad）该如何呢？可以人工激活该节点的梯度（微分）保存功能，即.retain_grad()。

尝试在Jupter中输入下述代码。需要注意的是：当一个张量开启了“requires_grad=True”时，其后续衍生的张量自动继承上述梯度计算功能，即可以从最终结果反向传播计算梯度；对于衍生的张量的“grad_fn”中会保存产生该张量的函数引用地址，该地址用于建立计算图后，反向传播时确定函数链。

# PyTorch提供自动微分机制，核心在于Tensor类的requires_grad=True和
# Function类的grad_fn函数，该函数表明了创建当前tensor的函数引用
import torchx = torch.ones(2, 2, requires_grad = True)
print("\n\nPyTorch的自动微分机制：")
print(x)y = x + 2   
# tensor + 2 = new tensorprint(y, y.requires_grad)    
# new tensor y具有了grad_fn属性
print(y.grad_fn)
y.retain_grad()
z = y * y * 3
out = z.mean()
print(z, out)
# out.backward(retain_graph = True)表示保存计算图
# out.backward（）默认等同于out.backward(torch.tensor(1.))
out.backward()
print("x.grad is:", x.grad)
print("y.grad is:", y.grad)

由于当因变量与自变量都是张量时计算十分繁琐，因而PyTorch不支持张量对张量求偏导，即仅支持张量对标量求梯度、标量对张量求梯度以及标量对标量求梯度。通常可以使用.sum()或.mean()等方法将张量转换为标量。

通常情况下，Loss函数以标量形式出现，不会触发PyTorch的求导限制。

模型训练阶段为了实现梯度下降多步骤迭代，PyTorch通常是针对需要拟合的变量进行梯度叠加，即第一步计算x_1=x-grad_1，第二步继续计算x_2=x_1-grad_2，如此循环往复直至Loss小于要求。

模式测试阶段通常不希望梯度自动叠加计算，此时需要暂停相关功能，可以使用with torch.no_grad():实现。

print(x.requires_grad)
print((x ** 2).requires_grad)
with torch.no_grad():
    print((x ** 2).requires_grad)

04 | 定义一个简单的NN

有了上述关于PyTorch的基础知识，接下来我们尝试定义一个简单的NN（神经网络）。

• 第一步需要在torch.nn.Module基类基础上，构造我们自己的NN类；
• 第二步需要实例化上述NN类对象；
• 第三步需要准备好输入数据；
• 第四步需要计算Loss函数；
• 第五步需要结合Loss函数进行梯度下降与参数更新。

整体代码如下，需要注意的是：

loss.backward()遵循建立的计算图为每个requires_grad=True的节点计算梯度值（grad）；

optim.step()使用优化器包含的梯度下降算法更新参数值；

可以使用model.parameters()获取模型中所有可训练参数张量。

# 定义一个简单的神经网络
print("\n\n尝试一个简单的神经网络：")

import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

class Net(nn.Module):   # torch.nn.Moudle类提供了NN通用结构    
  	# 定义类构造函数    
    # 从父类继承构造函数    
    def __init__(self):        
      	print('\ninit model...')        
        super(Net, self).__init__()        
        # 卷积层        
        self.conv1 = nn.Conv2d(1, 6, 5)        
        self.conv2 = nn.Conv2d(6, 16, 5)        
        # 全连接层        
        self.fc1 = nn.Linear(16 * 5 * 5, 120)        
        self.fc2 = nn.Linear(120, 84)        
        self.fc3 = nn.Linear(84, 10)    
    # 定义前向传播（将构造的模块组织成模型网络    
    def forward(self, x):   # X表示输入        
      	# 在（2,2）窗口上进行最大池化        
        x = F.max_pool2d(F.relu(self.conv1(x)), (2,2))        
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)        
        x = x.view(-1, self.num_flat_features(x))        
        x = F.relu(self.fc1(x))        
        x = F.relu(self.fc2(x))        
        x = self.fc3(x)        
        return x       
    def num_flat_features(self, x):        
      	size = x.size()[1:]        
        num_features = 1        
        for s in size:            
          	num_features *= s        
            return num_features

# 实例化NN类
net = Net()
print(net)

# 模型可训练的参数可以通过net.parameters()返回
print("\ncheck model parameters...")
params = list(net.parameters())
print("net's parameters is:", len(params))
print(params[0].size())

# 测试用生成随机输入
print("\ngenerate input...")
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

# 计算MSE损失
target = torch.randn(10)
target = target.view(1, -1)
criterion = nn.MSELoss()

# 建立优化器进行梯度迭代
optimizer = optim.SGD(net.parameters(), lr=0.01)
# 重置参数梯度缓冲区
optimizer.zero_grad()
print("parameter before backward:")
print(params[0].data)print(params[0].grad)
loss = criterion(out, target)
loss.backward()    # 反向传播计算梯度
optimizer.step()   # 优化器更新参数
print("parameter after backward:")
print(params[0].data[:1, 0])
print(params[0].grad[:1, 0])

05 | 写在最后

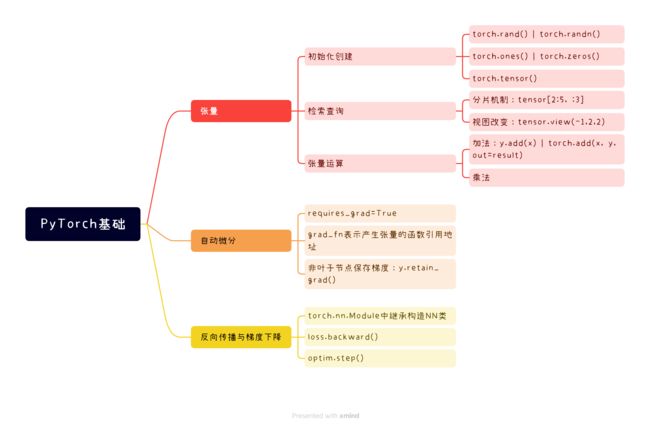
文末，我们尝试用导图的形式梳理下PyTorch快速入门所需要掌握的模块方法。