leetcode算法题之递归--综合练习(二)
本章目录
- 1.N皇后
- 2.有效的数独
- 3.解数独
- 4.单词搜索
- 5.黄金矿工
- 6.不同路径III
1.N皇后
N皇后
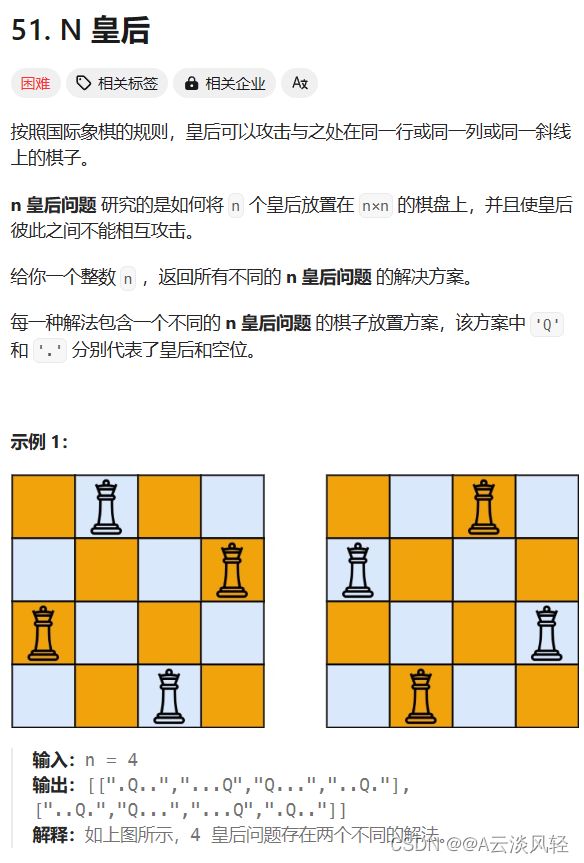
class Solution {
vector<vector<string>> ret;
vector<string> path;
int n;
bool checkCol[10],checkDig1[20],checkDig2[20];
public:
vector<vector<string>> solveNQueens(int _n) {
n = _n;
//初始化path
path.resize(n);
for(int i=0;i<n;i++)
{
path[i].append(n,'.');
}
dfs(0);
return ret;
}
void dfs(int row)
{
if(row == n)
{
ret.push_back(path);
return;
}
for(int col = 0;col<n;col++)
{
if(!checkCol[col]&& !checkDig1[col-row+n] && !checkDig2[col+row])
{
path[row][col] = 'Q';
checkCol[col] = checkDig1[col-row+n] = checkDig2[col+row] = true;
dfs(row+1);
path[row][col] = '.';
checkCol[col] = checkDig1[col-row+n] = checkDig2[col+row] = false;
}
}
}
};
2.有效的数独
有效的数独
class Solution {
bool row[9][10];
bool col[9][10];
bool grid[3][3][10];
public:
bool isValidSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
{
if(board[i][j]!='.')
{
int num = board[i][j]-'0';
if(row[i][num] || col[j][num] || grid[i/3][j/3][num])
{
return false;
}
row[i][num] = col[j][num] = grid[i/3][j/3][num] = true;
}
}
}
return true;
}
};
3.解数独
解数独
class Solution {
bool row[9][10];
bool col[9][10];
bool grid[3][3][10];
public:
void solveSudoku(vector<vector<char>>& board) {
//初始化一下row,col,grid数组
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
{
if(board[i][j]!='.')
{
int num = board[i][j]-'0';
row[i][num] = col[j][num] = grid[i/3][j/3][num] = true;
}
}
}
dfs(board);
}
bool dfs(vector<vector<char>>& board)
{
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
{
if(board[i][j]=='.')
{
for(int k=1;k<=9;k++)
{
if(!row[i][k] && !col[j][k] && !grid[i/3][j/3][k])
{
board[i][j] = '0'+k;
row[i][k] = col[j][k] = grid[i/3][j/3][k] = true;
if(dfs(board) == true) return true;
board[i][j] = '.';
row[i][k] = col[j][k] = grid[i/3][j/3][k] = false;
}
}
return false;
}
}
}
return true;
}
};
4.单词搜索
单词搜索
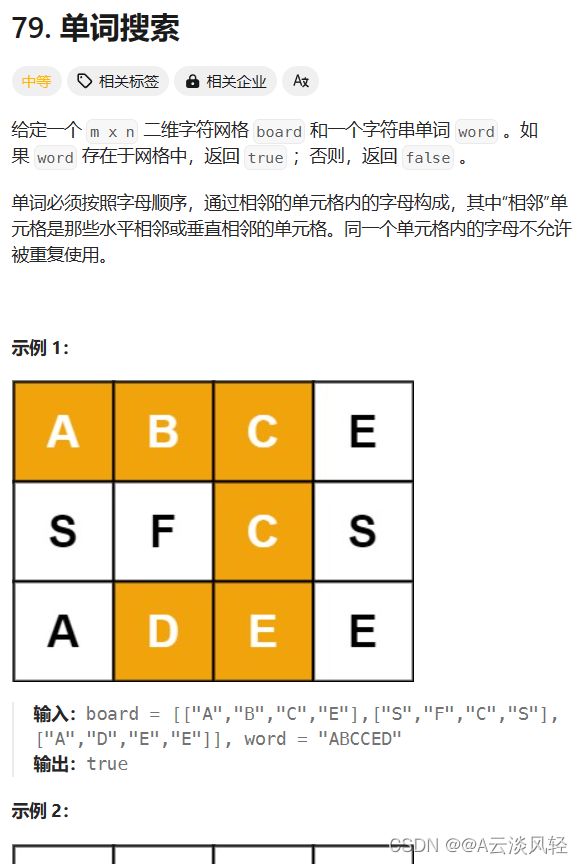
class Solution {
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
bool vis[7][7];
int m,n;
public:
bool exist(vector<vector<char>>& board, string word) {
m = board.size(), n = board[0].size();
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(board[i][j] == word[0])
{
vis[i][j] = true;
if(dfs(board,i,j,word,1)==true) return true;
vis[i][j] = false;
}
}
}
return false;
}
bool dfs(vector<vector<char>>& board,int i,int j,string& word,int pos)
{
if(pos == word.size())
{
return true;
}
for(int k=0;k<4;k++)
{
int x = i+dx[k],y = j+dy[k];
if(x>=0 && x<m && y>=0 && y<n && !vis[x][y]&& board[x][y] == word[pos])
{
vis[x][y] = true;
if(dfs(board,x,y,word,pos+1)) return true;
vis[x][y] = false;
}
}
return false;
}
};
5.黄金矿工
黄金矿工
class Solution {
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
bool vis[16][16];
int m,n;
int ret = 0;
public:
int getMaximumGold(vector<vector<int>>& grid) {
//暴搜，每个点都进行一次深搜
m = grid.size(),n = grid[0].size();
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j])
{
vis[i][j] = true;
dfs(grid,i,j,grid[i][j]);
vis[i][j] = false;
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j,int path)
{
ret = max(ret,path);
for(int k=0;k<4;k++)
{
int x = i+dx[k],y = j+dy[k];
if(x>=0 && x<m && y>=0 && y<n && !vis[x][y] && grid[x][y]!=0)
{
vis[x][y] = true;
dfs(grid,x,y,path+grid[x][y]);
vis[x][y] = false;
}
}
}
};
6.不同路径III
不同路径III
class Solution {
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
vector<vector<bool>> vis;
int m,n,step;
int ret;
public:
int uniquePathsIII(vector<vector<int>>& grid) {
m = grid.size(),n = grid[0].size();
vis = vector<vector<bool>>(m,vector<bool>(n));
int bx,by;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j] == 0) step++;
else if(grid[i][j] == 1)
{
bx = i;
by = j;
}
}
}
step += 2;
vis[bx][by] = true;
dfs(grid,bx,by,1);
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j,int count)
{
if(grid[i][j] == 2)
{
if(count == step) ret++;
return;
}
for(int k=0;k<4;k++)
{
int x = i+dx[k],y = j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y] && grid[x][y]!=-1)
{
vis[x][y] = true;
dfs(grid,x,y,count+1);
vis[x][y] = false;
}
}
}
};