分段低次插值(C++)
文章目录
- 分段线性插值
- 分段三次Hermite插值
- 三次样条插值
-
- 三弯矩算法
- 三转角算法
- 代码实现
-
- 分段线性插值
- 分段三次Hermite插值
- 三次样条插值
- 测试案例
由于实际应用时, 高次插值的逼近效果并不好, 因此需要将插值区间进行分段, 这就是分段低次插值. 通过对每两个数据点之间的小区间进行低次多项式插值来避免Runge现象, 并且可以有效地控制截断误差.
分段低次插值的具体做法因插值多项式的次数不同而有所差异. 例如, 分段线性插值就是将所有数据点用折线连起来, 得到的分段函数就是分段线性插值; 分段三次Hermite插值则是在任意一个小区间上进行两点三次Hermite插值等.
分段低次插值的优点在于可以有效地避免龙格现象和有效地控制截断误差, 缺点在于插值条件仅限定函数值在节点处相等, 导致插值函数的连续性较好, 但光滑性不高. 为了得到光滑性更好的插值函数, 需要对函数的导数进行约束.
分段线性插值
分段线性插值就是通过将相邻的两个插值点用线段连接, 如此形成的一条折线来逼近函数 f ( x ) f(x) f(x).
其余项估计为
∣ f ( x ) − I n ( x ) ∣ ⩽ h 2 8 M 2 |f(x)-I_n(x)|\leqslant\frac{h^2}8M_2 ∣f(x)−In(x)∣⩽8h2M2
其中, M 2 : = max a ⩽ x ⩽ b ∣ f ′ ′ ( x ) ∣ M_2:=\underset{a\leqslant x\leqslant b}{\text{max}}\big|f^{\prime\prime}(x)\big| M2:=a⩽x⩽bmax∣∣f′′(x)∣∣.
分段三次Hermite插值
分段三次Hermite插值就是在分段线性插值的基础上, 再给定每个节点处的一阶导数值, 则可以在每个小区间上构造一个3次Hermite多项式, 这就是分段三次Hermite插值.
特别地, 根据Lagrange型Hermite插值多项式, 可以给出每个区间上的Lagrange插值基函数如下:
α i ( x ) = { ( 1 + 2 x − x i x i − 1 − x i ) ( x − x i − 1 x i − x i − 1 ) 2 , x ∈ [ x i − 1 , x i ] ( 1 + 2 x − x i x i + 1 − x i ) ( x − x i + 1 x i − x i + 1 ) 2 , x ∈ [ x i , x i + 1 ] 0 , 其它 β i ( x ) = { ( x − x i ) ( x − x i − 1 x i − x i − 1 ) 2 , x ∈ [ x i − 1 , x i ] ( x − x i ) ( x − x i − 1 x i − x i + 1 ) 2 , x ∈ [ x i , x i + 1 ] 0 , 其它 \begin{aligned} \alpha_i(x)=\begin{cases} \begin{pmatrix}1+2\dfrac{x-x_i}{x_{i-1}-x_i}\end{pmatrix}\begin{pmatrix}\dfrac{x-x_{i-1}}{x_i-x_{i-1}}\end{pmatrix}^2&,x\in[x_{i-1},x_i]\\ \begin{pmatrix}1+2\dfrac{x-x_i}{x_{i+1}-x_i}\end{pmatrix}\begin{pmatrix}\dfrac{x-x_{i+1}}{x_i-x_{i+1}}\end{pmatrix}^2&,x\in[x_i,x_{i+1}]\\ 0&,\text{其它}\end{cases}\\ \beta_i(x)=\begin{cases}\left(x-x_i\right)\left(\dfrac{x-x_{i-1}}{x_i-x_{i-1}}\right)^2&,x\in\left[x_{i-1},x_i\right]\\ \left(x-x_i\right)\left(\dfrac{x-x_{i-1}}{x_i-x_{i+1}}\right)^2&,x\in\left[x_i,x_{i+1}\right]\\ 0&,\text{其它}\end{cases} \end{aligned} αi(x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧(1+2xi−1−xix−xi)(xi−xi−1x−xi−1)2(1+2xi+1−xix−xi)(xi−xi+1x−xi+1)20,x∈[xi−1,xi],x∈[xi,xi+1],其它βi(x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧(x−xi)(xi−xi−1x−xi−1)2(x−xi)(xi−xi+1x−xi−1)20,x∈[xi−1,xi],x∈[xi,xi+1],其它
分段三次Hermite插值的余项估计为
∣ f ( x ) − I n ( x ) ∣ ⩽ h 4 384 M 4 \big|f(x)-I_n(x)\big|\leqslant\dfrac{h^4}{384}M_4 ∣∣f(x)−In(x)∣∣⩽384h4M4
三次样条插值
由于高次插值难以计算并且存在Runge现象, 而分段线性插值不具有良好的光滑性. 尽管分段3次Hermite插值具有较好的光滑性, 但在实际应用中, 难以测得某观测点的导数值, 因此并不适用. 而三次样条插值就可以解决以上问题, 它的核心思想是在给定的一系列数据点上估计或插值出一个光滑的曲线.
三次样条插值通过分段三次多项式来逼近这条曲线. 具体来说, 我们首先根据观测点将区间分成 n n n段, 每段都使用一个三次多项式来逼近数据点. 为了使曲线光滑, 我们要求每个三次多项式的二阶导数在分段点处连续, 这样我们便拥有了 4 n − 2 4n-2 4n−2个条件. 这样, 再额外给定两个条件即可得到了一个由分段三次多项式构成的光滑插值曲线, 这两个条件被称为边界条件.
常见的边界条件有如下三种:
- m边界条件 即 S ′ ( x 0 ) = m 0 , S ′ ( x n ) = m n S^\prime(x_0)=m_0,S^\prime(x_n)=m_n S′(x0)=m0,S′(xn)=mn. 若 m 0 , m n m_0,m_n m0,mn由 x 0 , x 1 , x 2 , x 3 x_0,x_1,x_2,x_3 x0,x1,x2,x3和 x n − 3 , x n − 2 , x n − 1 , x n x_{n-3},x_{n-2},x_{n-1},x_n xn−3,xn−2,xn−1,xn进行3次Lagrange插值得到的多项式的1阶导数, 则称为Lagrange三次样条插值.
- M边界条件 即 S ′ ′ ( x 0 ) = M 0 , S ′ ′ ( x n ) = M n S^{\prime\prime}(x_0)=M_0,S^{\prime\prime}(x_n)=M_n S′′(x0)=M0,S′′(xn)=Mn. 若 M 0 = M n = 0 M_0=M_n=0 M0=Mn=0, 此时又称为自然边界条件, 所得的 S ( x ) S(x) S(x)称为自然样条函数.
- 周期边界条件 即 S ′ ( x 0 ) = S ′ ( x n ) , S ′ ′ ( x 0 ) = S ′ ′ ( x n ) S^\prime(x_0)=S^\prime(x_n),S^{\prime\prime}(x_0)=S^{\prime\prime}(x_n) S′(x0)=S′(xn),S′′(x0)=S′′(xn).
其余项估计为
∣ f ( k ) ( x ) − S ( k ) ( x ) ∣ ⩽ C k h 4 − k M 4 \left|f^{(k)}\left(x\right)-S^{(k)}\left(x\right)\right|\leqslant C_k h^{4-k}M_4 ∣∣∣f(k)(x)−S(k)(x)∣∣∣⩽Ckh4−kM4
其中, M 4 : = max a ⩽ x ⩽ b ∣ f ( 4 ) ( x ) ∣ M_4:=\max\limits_{a\leqslant x\leqslant b}|f^{(4)}(x)| M4:=a⩽x⩽bmax∣f(4)(x)∣, h : = max 0 ⩽ i ⩽ n − 1 ( x i + 1 − x i ) h:=\max\limits_{0\leqslant i\leqslant n-1}(x_{i+1}-x_i) h:=0⩽i⩽n−1max(xi+1−xi), 而 C k C_k Ck的前3项为 C 0 = 5 384 C_0=\dfrac5{384} C0=3845, C 1 = 1 24 C_1=\dfrac1{24} C1=241, C 2 = 1 8 C_2=\dfrac18 C2=81.
求解三次样条插值问题的常用算法有三弯矩算法和三转角算法, 具体如下.
三弯矩算法
三弯矩算法是一种用于求解三次样条插值的算法. 它通过给定的数据点, 计算出每个节点处的二阶导数值, 从而确定了每个区间的三次多项式插值函数.
三次样条插值函数 S ( x ) S(x) S(x)可以有多种表达方式, 有时用2阶导数值 M i : = S ′ ′ ( x i ) M_i:=S^{\prime\prime}(x_i) Mi:=S′′(xi)表示时使用更方便. 在力学上 M i M_i Mi解释为细梁在 x i x_i xi处的弯矩, 并且得到的弯矩与相邻两个弯矩有关, 故称用 M i M_i Mi表示 S ( x ) S(x) S(x)的算法为三弯矩算法.
由于 S ( x ) S(x) S(x)在区间 [ x i , x i + 1 ] [x_i,x_{i+1}] [xi,xi+1]上为3次多项式, 故 S ′ ′ ( x ) S^{\prime\prime}(x) S′′(x)在 [ x i , x i + 1 ] [x_i,x_{i+1}] [xi,xi+1]上为线性函数, 可表示为
S ′ ′ ( x ) = M i x i + 1 − x h i + M i + 1 x − x i h i S^{\prime\prime}(x)=M_i\frac{x_{i+1}-x}{h_i}+M_{i+1}\frac{x-x_i}{h_i} S′′(x)=Mihixi+1−x+Mi+1hix−xi
其中, h i : = x i + 1 − x i h_i:=x_{i+1}-x_i hi:=xi+1−xi. 积分两次, 并利用插值条件 S ( x i ) = f i , S ( x i + 1 ) = f i + 1 S(x_i)=f_i,S(x_{i+1})=f_{i+1} S(xi)=fi,S(xi+1)=fi+1可得
S ( x ) = M i ( x i + 1 − x ) 3 6 h i + M i + 1 ( x − x i ) 3 6 h i + ( f i − M i h i 2 6 ) x i + 1 − x h i + ( f i + 1 − M i + 1 h i 2 6 ) x − x i h i , x ∈ [ x i , x i + 1 ] S(x)=M_i\dfrac{\left(x_{i+1}-x\right)^3}{6h_i}+M_{i+1}\dfrac{\left(x-x_i\right)^3}{6h_i}+\left(f_i-\dfrac{M_i h_i^2}{6}\right)\dfrac{x_{i+1}-x}{h_i}+\left(f_{i+1}-\frac{M_{i+1}h_i^2}{6}\right)\frac{x-x_i}{h_i},x\in\left[x_i,x_{i+1}\right] S(x)=Mi6hi(xi+1−x)3+Mi+16hi(x−xi)3+(fi−6Mihi2)hixi+1−x+(fi+1−6Mi+1hi2)hix−xi,x∈[xi,xi+1]
因此只需求解 M i M_i Mi即可得到三次样条插值函数 S ( x ) S(x) S(x), 下面利用插值条件推导 M i M_i Mi的解法.
首先根据 M i M_i Mi的定义方式可得上式已经满足2阶导连续的条件, 由1阶导连续得:
μ i M i − 1 + 2 M i + λ i M i + 1 = d i , i = 1 , 2 , ⋯ , n − 1 \mu_{i}M_{i-1}+2M_{i}+\lambda_{i}M_{i+1}=d_{i},i=1,2,\cdots,n-1 μiMi−1+2Mi+λiMi+1=di,i=1,2,⋯,n−1
其中,
μ i : = h i − 1 h i − 1 + h i \mu_i:=\frac{h_{i-1}}{h_{i-1}+h_i} μi:=hi−1+hihi−1
λ i : = h i h i − 1 + h i = 1 − μ i \lambda_i:=\frac{h_i}{h_{i-1}+h_i}=1-\mu_i λi:=hi−1+hihi=1−μi
d i : = 6 f [ x i − 1 , x i , x i + 1 ] d_i:=6f[x_{i-1},x_i,x_{i+1}] di:=6f[xi−1,xi,xi+1]
这里有 n − 1 n-1 n−1个方程, 而剩下两个方程需要使用边界条件给出.
当边界条件为m型或M型时, 此时所得的方程组为三对角方程组, 在实现时可采用追赶法求解.
当边界条件为周期边界条件时, 此时所得的方程组为循环三对角方程组, 采用Sherman-Morrison方法求解.
三转角算法
与三弯矩算法不同的是, 三转角算法以一阶导 m i m_i mi来构造三次样条函数, 假设所有节点的一阶导数值已知, 可推导出如下公式:
S ( x ) = [ h i + 2 ( x − x i ) ] ( x − x i + 1 ) 2 h i 3 f i + [ h i + 2 ( x i + 1 − x ) ] ( x − x i ) 2 h i 3 f i + 1 + ( x − x i ) ( x − x i + 1 ) 2 h i 2 m i + + ( x − x i + 1 ) ( x − x i ) 2 h i 2 m i + 1 S(x)=\dfrac{\left[h_{i}+2(x-x_{i})\right](x-x_{i+1})^{2}}{h_{i}^{3}}f_{i}+\frac{\left[h_{i}+2(x_{i+1}-x)\right](x-x_{i})^{2}}{h_{i}^{3}}f_{i+1}+\dfrac{\left(x-x_i\right)\left(x-x_{i+1}\right)^2}{h_i^2}m_i++\dfrac{\left(x-x_{i+1}\right)\left(x-x_i\right)^2}{h_i^2}m_{i+1} S(x)=hi3[hi+2(x−xi)](x−xi+1)2fi+hi3[hi+2(xi+1−x)](x−xi)2fi+1+hi2(x−xi)(x−xi+1)2mi++hi2(x−xi+1)(x−xi)2mi+1
与三弯矩算法类似地可得如下公式:
λ i m i − 1 + 2 m i + μ i m i + 1 = e i , i = 1 , 2 , ⋯ , n − 1 \lambda_{i}m_{i-1}+2m_{i}+\mu_{i}m_{i+1}=e_{i},i=1,2,\cdots,n-1 λimi−1+2mi+μimi+1=ei,i=1,2,⋯,n−1
其中, λ i , μ i \lambda_i,\mu_i λi,μi同三弯矩算法, 而 e i : = 3 ( λ i f [ x i − 1 , x i ] + μ i f [ x i , x i + 1 ] ) e_i:=3(\lambda_if[x_{i-1},x_i]+\mu_if[x_i,x_{i+1}]) ei:=3(λif[xi−1,xi]+μif[xi,xi+1]).
代码实现
首先包含头文件如下:
#include 另外需要引入检查向量是否包含重复元素的函数, 见多项式插值法(基于c++,armadillo库):
namespace _MYFUNCTION {
extern bool check_unique(const vec&);
}
分段线性插值
/*
* 分段线性插值
* x0:观测点
* y0:观测数据
* x1:插值点
* y1:预测值
*/
void piecewise_linear_interpolation(const vec &x0, const mat &y0, const vec &x1, vec &y1)
{
if (x1.empty())
{
y1.clear();
return;
}
if (x0.empty() || y0.empty())
throw "观测集为空!";
if (y0.n_cols != 1)
throw "分段线性插值不需要导数信息!";
if (x0.n_elem != y0.n_elem)
throw "观测点与观测数据向量大小不一致!";
if (x0.n_elem == 1)
throw "观测点数量小于2!";
if (_MYFUNCTION::check_unique(x0))
throw "观测集包含重复元素!";
const unsigned &n0(x0.n_elem), &n1(x1.n_elem);
vec vx0(x0);
uvec index(sort_index(x0));
vx0.elem(index);
mat vy0(y0.rows(index));
y1.set_size(n1);
unsigned u(n1);
double *begin(&vx0.at(0)), *end(&vx0.at(n0 - 1)), *ybegin(&vy0.at(0)), *yend(&vy0.at(n0 - 1));
do
{
const double &x(x1.at(--u));
double *i(begin), *j(end);
if (x < *i)
y1.at(u) = *ybegin + (*(ybegin + 1) - *ybegin) * (x - *begin) / (*(begin + 1) - *begin);
else if (x > *j)
y1.at(u) = *yend + (*(yend - 1) - *yend) * (x - *end) / (*(end - 1) - *end);
else
{
do // 二分查找
{
double *m(i + (j - i) / 2);
if (*m > x)
--(j = m);
else
++(i = m);
} while (i <= j);
unsigned k(i - begin);
double *yi(ybegin + k), *yj(yi - 1);
y1.at(u) = *yj + (*yi - *yj) * (x - *j) / (*i - *j);
}
} while (u);
}
分段三次Hermite插值
/*
* 分段Hermite插值
* x0:观测点
* y0:观测数据(第i列为i阶导数)
* x1:插值点
* y1:预测值
*/
void piecewise_Hermite_interpolation(const vec &x0, const mat &y0, const vec &x1, vec &y1)
{
if (x1.empty())
{
y1.clear();
return;
}
if (x0.empty() || y0.empty())
throw "观测集为空!";
if (y0.n_cols != 2)
throw "导数信息有误!";
if (x0.n_elem != y0.n_rows)
throw "观测点与观测数据向量大小不一致!";
if (x0.n_elem == 1)
throw "观测点数量小于2!";
if (_MYFUNCTION::check_unique(x0))
throw "观测集包含重复元素!";
const unsigned &n0(x0.n_elem), &n1(x1.n_elem);
vec vx0(x0);
uvec index(sort_index(x0));
vx0.elem(index);
mat vy0(y0.rows(index));
y1.set_size(n1);
unsigned u(n1);
double *begin(&vx0.at(0)), *end(&vx0.at(n0 - 1)), *ybegin(&vy0.at(0)), *yend(&vy0.at(n0 - 1)), *dybegin(&vy0.at(0, 1)), *dyend(&vy0.at(n0 - 1, 1)), &begin1(*(begin + 1)), &ybegin1(*(ybegin + 1)), &dybegin1(*(dybegin + 1)), &end1(*(end - 1)), ¥d1(*(yend - 1)), &dyend1(*(dyend - 1));
do
{
const double &x(x1.at(--u));
double *i(begin), *j(end);
if (x < *i)
{
double d0(x - *begin), d1(x - begin1), t1(d0 / (begin1 - *begin)), t0(d1 / (*begin - begin1)), t12(t1), t02(t0);
t12 *= t1;
t02 *= t0;
y1.at(u) = ybegin1 * (1 + 2 * t0) * t12 + *ybegin * (1 + 2 * t1) * t02 + *dybegin * d0 * t02 + dybegin1 * d1 * t12;
}
else if (x > *j)
{
double d0(x - *end), d1(x - end1), t0(d1 / (*end - end1)), t1(d0 / (end1 - *end)), t02(t0), t12(t1);
t02 *= t0;
t12 *= t1;
y1.at(u) = *yend * (1 + 2 * t1) * t02 + yend1 * (1 + 2 * t0) * t12 + *dyend * d0 * t02 + dyend1 * d1 * t12;
}
else
{
do // 二分查找
{
double *m(i + (j - i) / 2);
if (*m > x)
--(j = m);
else
++(i = m);
} while (i <= j);
unsigned k(i - begin), l(j - begin);
double d0(x - *j), d1(x - *i), t0(d1 / (*j - *i)), t1(d0 / (*i - *j)), t02(t0), t12(t1);
t02 *= t0, t12 *= t1;
y1.at(u) = ybegin[l] * (1 + 2 * t1) * t02 + ybegin[k] * (1 + 2 * t0) * t12 + dybegin[l] * d0 * t02 + dybegin[k] * d1 * t12;
}
} while (u);
}
三次样条插值
这里使用三弯矩算法, 感兴趣的读者可以类似实现三转角算法.
首先定义一个边界条件类, 虽然不能表示所有边界条件, 但覆盖了常见的3种边界条件.
// 边界条件
struct boundary_conditions
{
unsigned char t; // 边界条件类型
// 第1位: 0:m/M型 1:周期边界条件
// 第2位: 0:第0个节点取1阶导 1:第0个节点取2阶导
// 第3位: 0:第n个节点取1阶导 1:第n个节点取2阶导
double y1, y2;
// 默认构造:周期边界
boundary_conditions() : t('\1') {}
boundary_conditions(unsigned char k, const double &w1 = 0.0, const double &w2 = 0.0) : t(k), y1(w1), y2(w2) {}
};
// Lagrange型边界条件
// 不检查x,y的维数匹配, x元素是否唯一及元素个数问题
boundary_conditions &Lagrange_boundary(const vec &x, const mat &y, boundary_conditions &B) noexcept
{
B.t = '\0';
const double *xb(&x.at(0)), *xe(xb + x.n_elem), &x0(*xb), &x1(*++xb), &x2(*++xb), &x3(*++xb), *yb(&y.at(0)), *ye(yb + x.n_elem), &y0(*yb), &y1(*++yb), &y2(*++yb), &y3(*++yb), &u3(*--xe), &u2(*--xe), &u1(*--xe), &u0(*--xe), &v3(*--ye), &v2(*--ye), &v1(*--ye), &v0(*--ye);
double x02(x0 - x2), x03(x0 - x3), x01(x0 - x1), x12(x1 - x2), x13(x1 - x3), x23(x2 - x3);
B.y1 = y0 / x02 + y0 / x03 + y0 / x01 - y1 * x02 * x03 / x12 / x13 / x01 + y2 * x01 * x03 / x23 / x02 / x12 - y3 * x01 * x02 / x03 / x13 / x23;
double u01(u0 - u1), u02(u0 - u2), u03(u0 - u3), u12(u1 - u2), u13(u1 - u3), u23(u2 - u3);
B.y2 = v0 * u13 * u23 / u01 / u02 / u03 - v3 / u13 - v3 / u23 - v1 * u03 * u23 / u12 / u13 / u01 + v2 * u03 * u13 / u23 / u02 / u12 - v3 / u03;
return B;
}
接着实现三弯矩算法:
/*
* 三弯矩算法
* x0:观测点
* y0:观测数据
* x1:插值点
* y1:预测值
* B :边界条件
*/
void Three_moment_algorithm(const vec &x0, const mat &y0, const vec &x1, vec &y1, const boundary_conditions &B)
{
if (x1.empty())
{
y1.clear();
return;
}
if (x0.empty() || y0.empty())
throw "观测集为空!";
if (y0.n_cols != 1)
throw "三次样条插值不需要导数信息!";
if (x0.n_elem != y0.n_elem)
throw "观测点与观测数据向量大小不一致!";
if (x0.n_elem < 4u)
throw "观测点数量小于4!";
if (_MYFUNCTION::check_unique(x0))
throw "观测集包含重复元素!";
vec vx0(x0);
uvec index(sort_index(x0));
vx0.elem(index);
mat vy0(y0.rows(index));
const unsigned n0(x0.n_elem), n1(x1.n_elem), n(n0 - 1);
double *lambda(new double[n]), *mu(new double[n]), *M(new double[n0]), *d(new double[n0]), *l_p(lambda + n), *m_p(mu + n), *M_p(M), *d_p(d + n), *diff(new double[n] + n), *diffp(diff), *h(new double[n] + n), *h_p(h);
double *xb(&vx0.at(0)), *yb(&vy0.at(0)), *xe(xb + n0), *ye(yb + n0), *xp(xe), *yp(ye);
while (--yp, --xp != xb)
*--diff = (*yp - *(yp - 1)) / (*--h = *xp - *(xp - 1));
if (B.t & '\1')
{
double h_0n(*h + *--h_p);
*--m_p = 1 - (*--l_p = *h / h_0n);
*--d_p = 6 * (*diff - *--diffp) / h_0n;
do
{
const double &th(*h_p), &tdiff(*diffp);
double t(*--h_p + th);
*--m_p = 1 - (*--l_p = th / t);
*--d_p = 6 * (tdiff - *--diffp) / t;
} while (m_p != mu);
if (!*l_p)
{
delete[] lambda;
delete[] mu;
delete[] M;
delete[] d;
delete[] diff;
delete[] h;
throw "分母为零!";
}
if (n == 3u)
{ // 直接使用Cramer法则求解
double &mu0(*mu), &mu1(*++m_p), &mu2(*++m_p), &lambda0(*lambda), &lambda1(*++l_p), &lambda2(*++l_p), &d0(*d), &d1(*++d_p), &d2(*++d_p), D(8 + mu0 * mu1 * mu2 + lambda0 * lambda1 * lambda2 - 2 * lambda2 * mu0 - mu1 * lambda0 * 2 - 2 * mu2 * lambda1);
if (!D)
{
delete[] lambda;
delete[] mu;
delete[] M;
delete[] d;
delete[] diff;
delete[] h;
throw "分母为零!";
}
*M = *(M_p += 3) = (4 * d2 + mu1 * mu2 * d0 + lambda2 * lambda0 * d1 - 2 * lambda2 * d0 - mu1 * lambda0 * d2 - 2 * mu2 * d1) / D;
*--M_p = (4 * d1 + mu1 * d2 * mu0 + mu2 * d0 * lambda1 - mu2 * d1 * mu0 - mu1 * d0 * 2 - 2 * d2 * lambda1) / D;
*--M_p = (4 * d0 + d1 * mu2 * mu0 + d2 * lambda0 * lambda1 - d2 * 2 * mu0 - d1 * lambda0 * 2 - d0 * mu2 * lambda1) / D;
}
else
{
// Sherman-Morrison方法求解循环三对角方程组
// 接下来diff没用了, 分别将diff和t看作向量y和q
double *t(new double[n]), *t_p(t), &t_2(*++t_p = 2 / *l_p);
*t = -2 * t_2;
*++d_p -= 2 * (*++diffp = *d / *l_p++);
*diff = *++m_p;
*++d_p -= *++m_p * *diffp;
*++t_p = -*m_p * t_2;
*++diffp = 2;
unsigned i(n), k(i -= 3);
while (--i)
{
if (!*diffp)
{
delete[] lambda;
delete[] mu;
delete[] M;
delete[] d;
delete[] diff;
delete[] h;
delete[] t;
throw "分母为零!";
}
double m(*++m_p / *diffp), &d_k(*d_p);
*++diffp = 2 - m * *++l_p;
*++d_p -= m * d_k;
*++t_p = -2 * m;
}
// 注意到x_k的表达式只与d_k,b_k有关, 与d_{k+1},b_{k+1}无关
if (!*diffp)
{
delete[] lambda;
delete[] mu;
delete[] M;
delete[] d;
delete[] diff;
delete[] h;
delete[] t;
throw "分母为零!";
}
double m(*++m_p / *diffp);
double &d_k(*d_p), &l_k(*++l_p), vn(*mu / 2), Ann(2 - vn * *++l_p);
if (!(Ann -= m * l_k))
{
delete[] lambda;
delete[] mu;
delete[] M;
delete[] d;
delete[] diff;
delete[] h;
delete[] t;
throw "分母为零!";
}
double &xk(*++diffp = (*++d_p -= m * d_k) / Ann), &bk(*--diffp), &qdk(*t_p), &qxk(*(++t_p)-- = (*l_p - m * qdk) / Ann);
(qdk -= *l_p * qxk) /= bk;
bk = (*--d_p - *l_p * xk) / bk;
while (--k)
{
double &xk(*diffp), &bk(*--diffp), &qxk(*t_p), &qdk(*--t_p);
(qdk -= *--l_p * qxk) /= bk;
bk = (*--d_p - *l_p * xk) / bk;
}
(*t -= *--l_p * *t_p) /= *diff;
*diff = (*--d_p - *l_p * *diffp) / *diff;
--(i = n);
double dot_c((*diff + vn * *(diffp = diff + i)) / (1 + *t + vn * *(t_p = t + i)));
*M = *(M_p += n) = *(diffp = diff + i) - dot_c * *(t_p = t + i);
do
*--M_p = *--diffp - dot_c * *--t_p;
while (--i);
delete[] t;
}
}
else
{
--h_p, --diffp;
if (B.t & '\4')
{
*d_p = 2 * B.y2;
*--m_p = 0;
}
else
{
*d_p = 6 * (B.y2 - *diffp) / *h_p;
*--m_p = 1;
}
if (B.t & '\2')
{
*d = 2 * B.y1;
*lambda = 0;
}
else
{
*d = 6 * (B.y1 - *diff) / *h;
*lambda = 1;
}
do
{
double &hi(*h_p), &diffi(*diffp), t(*--h_p + hi);
*--m_p = 1 - (*--l_p = hi / t);
*--d_p = 6 * (diffi - *--diffp) / t;
} while (mu != m_p);
// 追赶法求解
unsigned i(n);
double m(*m_p / (*M = 2));
*++M_p = 2 - m * *--l_p;
*d_p -= m * *d;
while (--i)
{
double m(*++m_p / *M_p), &td(*d_p);
*++M_p = 2 - m * *++l_p;
*++d_p -= m * td;
}
*M_p = *d_p / *M_p;
++l_p;
do
{
double &preM(*M_p--);
*M_p = (*--d_p - *--l_p * preM) / *M_p;
} while (M_p != M);
}
delete[] lambda;
delete[] mu;
delete[] d;
delete[] diff;
y1.set_size(n1);
unsigned u(n1);
double &M0(*M), &M1(M[1]), &X0(*xb), &X1(xb[1]), &Y0(*yb), &Y1(yb[1]), &XE(*(xe - 1)), &XE1(*(xe - 2)), &YE(*(ye - 1)), &YE1(*(ye - 2)), &ME(M[n]), &ME1(M[n - 1]);
do
{
const double &x(x1.at(--u));
if (*xb >= x)
{
double Dx1(X1 - x), Dx13(Dx1), Dx0(x - X0), Dx03(Dx0), &hi(*h), hi2(hi * hi / 6);
(y1.at(u) = (M0 * ((Dx13 *= Dx1) *= Dx1) + M1 * ((Dx03 *= Dx0) *= Dx0)) / 6 + (Y0 - M0 * hi2) * Dx1 + (Y1 - M1 * hi2) * Dx0) /= hi;
continue;
}
if (XE < x)
{
double Dx1(XE - x), Dx13(Dx1), Dx0(x - XE1), Dx03(Dx0), &hi(h[n]), hi2(hi * hi / 6);
(y1.at(u) = (ME1 * ((Dx13 *= Dx1) *= Dx1) + ME * ((Dx03 *= Dx0) *= Dx0)) / 6 + (YE1 - ME1 * hi2) * Dx1 + (YE - ME * hi2) * Dx0) /= hi;
continue;
}
double *j(lower_bound(xb, xe, x)), *i(j), Dx1(*j - x), Dx13(Dx1), Dx0(x - *--i), Dx03(Dx0);
unsigned k(i - xb), l(k);
double &hi(h[k]), hi2(hi * hi / 6), &M0(M[k]), &M1(M[++k]);
(y1.at(u) = (M0 * ((Dx13 *= Dx1) *= Dx1) + M1 * ((Dx03 *= Dx0) *= Dx0)) / 6 + (yb[l] - M0 * hi2) * Dx1 + (yb[k] - M1 * hi2) * Dx0) /= hi;
} while (u);
delete[] M;
delete[] h;
}
测试案例
用分段低次插值法对函数 f ( x ) = 1 1 + 25 x 2 f(x)=\dfrac1{1+25x^2} f(x)=1+25x21插值, 观测点为步长为0.2的等分点.
编写测试代码如下:
#include 运行后利用Origin绘图, 首先可得分段线性插值如下:

其误差如下:

分段Hermite插值结果如下:
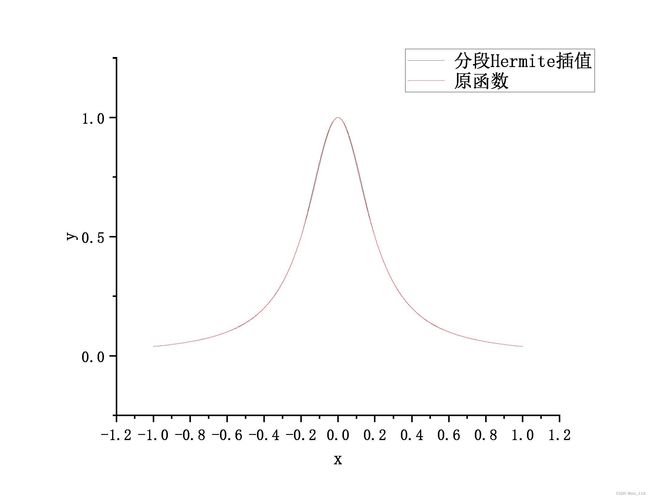
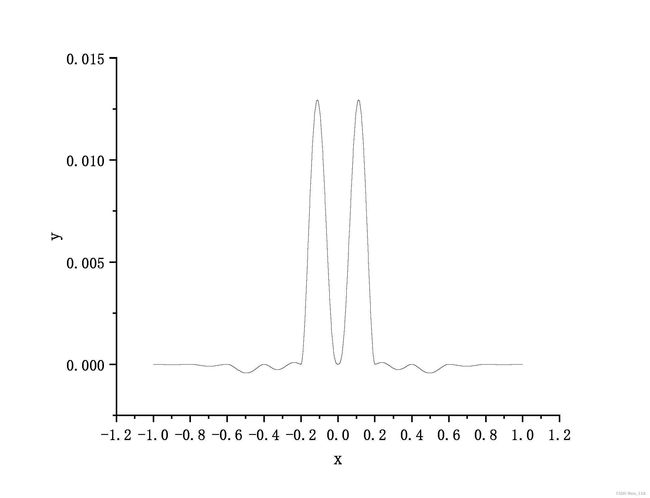
其误差为:
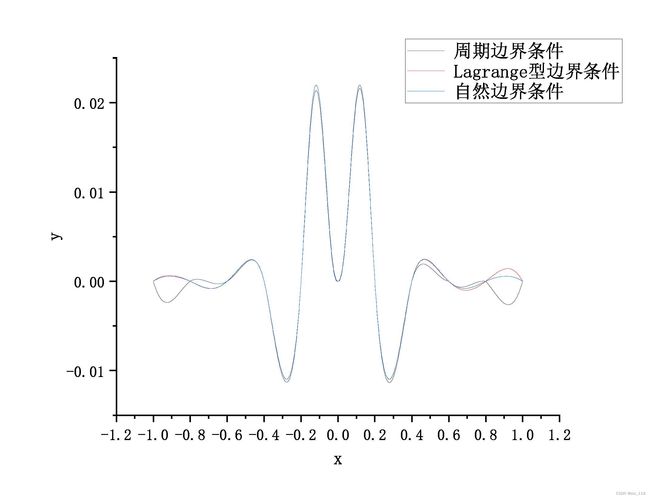
三次样条插值结果如下:

其误差为: