线性规划求解

线性规划概念介绍

线性规划是优化问题的特殊情形，其模型中的目标函数和约束条件均为决策变量的线性函数。

模型建立步骤

1. 确定决策变量
2. 确定目标函数
3. 确定约束条件

基本的线性模型例子

列1【合理下料问题】用长度为500厘米的条材，截成长度为98厘米和78厘米两种毛胚，要求长98厘米的毛胚1000根，78厘米长的毛胚2000更，应增氧才能使所用的原材料最少，试建立问题的数学模型。
解一根500厘米的条材截成98厘米和78厘米长度的毛胚有很多种方案，列出方案表如下：

方案序号	98厘米毛胚数	78厘米毛胚数	剩余厘米数
1	0	6	32
2	1	5	12
3	2	4	70
4	3	3	50
5	4	2	30
6	5	1	10

设决策变量x_i($1\le i\le 6$)表示第i个方案所用的条材数。目标函数可以表示为：
$minz=x_1+x_2+x_3+x_4+x_5+x_6$
约束条件就是
$$\{\begin{array}{c}{x}_2+2x_3+3x_4+4x_5+5x_6\ge 1000\\ 6x_1+5x_2+3x_3+2x_4+x_5\ge 2000\\ x_1,x_2,\dots ,x_6\ge 0且取整数\end{array}$$
由于是实际问题，决策变量应该取非负整数。

列2【0-1背包问题】一个旅行者要在背包里装一些最有用的旅行物品。背包容积为a，携带物品总质量最多为b。现有物品m件，第j件物品体积为a_j，质量为b_j（j=1,2,…,m）。为了比较物品的有用程度，假设第j件物品的价值是c_j（j=1,2,…,m）。若每件物品只能携带整件，每件物品都能放入背包，并且不考虑放入背包里面的间隙。问旅行者应当携带那几件物品才能使得物品的总价值最大？试建立问题的数学模型。
解每件物品有被选择和不被选择两种可能，为此，设$x_j$为第j件物品装入的数量，则对应于m件物品引入m个0-1变量：

$$x_j=\{\begin{array}{ll}1,& \text{(携带第j件物品)}\\ 0,& \text{(不携带第j件物品)}（j=1,2,...,m）\end{array}$$
目标函数=物品携带的总价值 $z={\sum }_{j=1}^m{c}_j{x}_j$
约束条件，所携带的物品总体积不超过a，总质量不超过b
数学模型如下：
z=${\sum }_{j=1}^m{c}_j{x}_j$
$$s.t.=\{\begin{array}{c}{\sum }_{j=1}^m{a}_j{x}_j\le a\\ \\ {\sum }_{j=1}^m{b}_j{x}_j\le b\\ \\ x_j=0或1（j=1,2,...,m）\end{array}$$
该模型决策变量x只能取0或1，成为0-1整数规划，简称0-1规划。

列3【运输问题】某公司有3个同类产品的工厂（简称产地A_i，i=1,2,3），生产的产品由4个销售点（简称销售地B_i，i=1,2,3,4）销售，各工厂的生产量（用a_i表示），各销售点的销量（用b_j表示）以及各工厂到销售点的单位产品运价（用c_ij表示）如表2.3表示。问该公司应如何调运产品，在满足各销售点的需求量的前提下，使总的运费最少？
表2.3 产量、销量与单位产品运价关系表

产地\单位运价\销地	B1	B2	B3	B4	产量ai
A1	3	11	3	10	7
A2	1	9	2	8	4
A3	7	4	10	5	9
销量bj	3	6	5	6	-

解本问题中“如何制定调运方案”，就是指的安排一个产地和一个销地各应安排多大的运量，因此令从产地 A_i到销地B_j的运量为x_ij（i=1,2,3;j=1,2,3,4）作为本问题的决策变量。
目标函数=总运费=$z={\sum }_{i=1}^3{\sum }_{j=1}^4{c}_{ij}{x}_{ij}$
约束条件：由表2.3可知，运输问题的总产量（7+4+9）=总销量（3+6+5+6），所以运输问题是平衡运输问题。第一个约束条件是：各产地运往某一销地的物品数量之和等于该销地的销量，即${\sum }_{i=1}^3{x}_{ij}=b_j(j=1,2,3,4)$,第二个约束条件：某一产地运往各销售地的物品数量之和等于该地的产量，即${\sum }_{j=1}^4{x}_{ij}=a_i(i=1,2,3)$，第三个约束条件：决策变量为非负，即$x_{ij}\ge 0(i=1,2,3;j=1,2,3,4)$。
因此数学模型可表述如下：
$minz={\sum }_{i=1}^3{\sum }_{j=1}^4{c}_{ij}{x}_{ij}$
$$s.t.=\{\begin{array}{c}{\sum }_{i=1}^3{x}_{ij}=b_j(j=1,2,3,4)\\ \\ {\sum }_{j=1}^4{x}_{ij}=a_i(i=1,2,3)\\ \\ x_{ij}\ge 0(i=1,2,3;j=1,2,3,4)\end{array}$$

模型一般形式和标准形式

一般形式：
$max(min)z=c_1{x}_1+c_2{x}_2+\dots +c_n{x}_n$
$$s.t.=\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+\dots +a_{1n}{x}_n\le (=,\ge )b_1\\ \\ a_{21}{x}_1+a_{22}{x}_2+\dots +a_{2n}{x}_n\le (=,\ge )b_2\\ \\ ......\\ \\ a_{m1}{x}_1+a_{m2}{x}_2+\dots +a_{mn}{x}_n\le (=,\ge )b_2\\ \\ x_1,x_2,...,x_n\ge 0\end{array}$$
标准形式(也就是把一般形式的不等式转换成等式，目标函数一般转化为min方便后面求解)：
$minz={\sum }_{j=1}^n{c}_j{x}_j$
$$s.t.=\{\begin{array}{c}{\sum }_{j=1}^n{a}_{ij}{x}_j=b_i(i=1...,m)\\ \\ x_j\ge 0(j=1,...,n)\end{array}$$
转化方法：
首先先将x全部转化为$\ge$,之后转变约束条件：对于小于的不等式，加一个松弛变量，对于大于的不等式，减一个松弛变量，之后是：目标函数$max变min$，整体乘-1就可以了。
例如：将下列线性规划转化为标准模型
$maxz=5x_1-2x_2+3x_3$
$$s.t.=\{\begin{array}{c}2x_1-x_2+5x_3\ge -1\\ \\ x_1+x-3\le 2\\ \\ x_1\le 0,x_2\ge 0,x_3无约束\end{array}$$
分析：$$\begin{gathered} x_1\le 0于是设x_1^{\prime }\ge 0,x_1=-x_1^{\prime }; \\ {x}_3无约束,设x_3^{\prime },x_3^{\prime \prime }\ge 0,x_3=x_3^{\prime }-x_3^{\prime \prime } \\ {x}_4,x_5\ge 0作为两个不等式的松弛变量 \end{gathered}$$
转化标准型为：
$min{z}^{\prime }=-z=-5x_1+2x_2-3x_3$
$$s.t.=\{\begin{array}{c}2x_1^{\prime }+x_2-5x_3^{\prime }+5x_3^{\prime \prime }+x_4=1\\ \\ -x_1^{\prime }+x_3^{\prime }-x_3^{\prime \prime }+x_5=2\\ \\ x_1^{\prime },x_2,x_3^{\prime },x_3^{\prime \prime },x_4,x_5\ge 0\end{array}$$

单纯形法、大M法、两阶段法

1）单纯形法
理论很复杂直接上题
列1单纯形法求解下列线性规划
$minz=x_1-2x_2+x_3$
$$s.t.=\{\begin{array}{c}{x}_1+x_2-2x_3+x_4=10\\ \\ 2x_1-x_2+4x_3\le 8\\ \\ -x_1+2x_2-4x_3\le 4\\ \\ x_j\ge 0,j=1,2,3,4\end{array}$$
解：A转化为标准形式：
$minz=x_1-2x_2+x_3+0x_4+0x_5+0x_6$
$$s.t.=\{\begin{array}{c}{x}_1+x_2-2x_3+x_4=10\\ \\ 2x_1-x_2+4x_3+x_5=8\\ \\ -x_1+2x_2-4x_3+x_6=4\\ \\ x_j\ge 0,j=1,2,3,4,5,6\end{array}$$
B列出单纯形表如下：

	Cj		|	1	-2	1	0	0	0
$C_B$	$x_b$	b	|	x1	x2	x3	x4	x5	x6
0	x4	10	|	1	1	-2	1	0	0
0	x5	8	|	2	-1	4	0	1	0
0	x6	2	|	-1	2	-4	0	0	1
	${\partial }_j$		|	1	2	-1	0	0	0

C_j表示的是目标函数对应x_j的系数，在系数行列式里面选取一个单位矩阵，得到的三个变量就是x₄，x₅，x₆。
b表示的不等式右边的数字
最后一行 ${\partial }_j$是检验数，极小问题的结束条件就是检验数全部都是正数，极大问题的结束条件就是检验数全部都是负数。
$${\partial }_1=C_j-C_B\ast x_1=1-\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\left(\begin{array}{c}2\\ -1\\ -1\end{array}\right)=1$$
C求解
由于检验数 ${\partial }_j$不全大于0于是选取负数中最小的，在这一列里面找非负的数对应的x就是入基，让b/对应的数，取最小的就是出基。

	Cj		|	1	-2	1	0	0	0
$C_B$	$x_b$	b	|	x1	x2	x3	x4	x5	x6	$\nabla$
0	x4	10	|	1	1	-2	1	0	0	10/1
0	x5	8	|	2	-1	4	0	1	0
0	x6	2	|	-1	[2]	-4	0	0	1	4/2
	${\partial }_j$		|	1	-2	1	0	0	0

用x₂代替x₆,化这个数字2为1，这列其他的数为0继续单纯形法,替代只需要修改变量和系数，即0 x₆变成-2 x₂，其他的不需要变。
$$\begin{array}{rrrrrccccc}& C_B& x_b& b& x_1& x_2& x_3& x_4& x_5& x_6\\ & & & & & & & & & \\ & 0& x_4& 8& \frac{3}{2}& 0& 0& 1& 0& -\frac{1}{2}\\ & & & & & & & & & \\ & 0& x_5& 10& \frac{3}{2}& 0& [2]& 0& 1& \frac{1}{2}\\ & & & & & & & & & \\ & -2& x_2& 2& -\frac{1}{2}& 1& -2& 0& 0& \frac{1}{2}\\ & & & & & & & & & \\ & & & & & & & & & \\ & & {\partial }_j& & 0& 0& -3& 0& 0& 1\end{array}$$
$确定入基为x_3，出基为x_5，继续单纯形法为：$
$$\begin{array}{rrrrrccccc}& C_B& x_b& b& x_1& x_2& x_3& x_4& x_5& x_6\\ & & & & & & & & & \\ & 0& x_4& 8& \frac{3}{2}& 0& 0& 1& 0& -\frac{1}{2}\\ & & & & & & & & & \\ & 1& x_3& 5& \frac{3}{4}& 0& 1& 0& \frac{1}{2}& \frac{1}{4}\\ & & & & & & & & & \\ & -2& x_2& 12& 1& 1& 0& 0& 1& 1\\ & & & & & & & & & \\ & & & & & & & & & \\ & & {\partial }_j& & \frac{9}{4}& 0& 0& 0& \frac{3}{2}& \frac{7}{4}\end{array}$$
此时所有的${\partial }_j\ge 0$,达到结束条件，此时的b这一行就是x的取值，其他的都是0
$x_2=12,x_3=5,x_4=8,x_1=x_5=x_6=0$
由于目标函数只包含$x_1,x_2,x_3$,于是最优解X^*=(0,12,5,8)^T
2）大M法
这个M是值很大的正数
列：使用大M法求解下列线性规划
max z=-3x₁+x₃
$$s.t.=\{\begin{array}{c}{x}_1+x_2+x_3\le 4\\ \\ -2x_1+x_2-x_3\ge 1\\ \\ 3x_2+x_3=9\\ \\ x_1{x}_2,x_3\ge 0\end{array}$$
转化为标准形式
$min{z}^{\prime }=3x_1-x_3$
$$s.t.=\{\begin{array}{c}{x}_1+x_2+x_3+x_5=4\\ \\ -2x_1+x_2-x_3-x_5=1\\ \\ 3x_2+x_3=9\\ \\ x_1{x}_2,x_3,x_4,x_5\ge 0\end{array}$$
列出系数矩阵如下
$$A=\left[\begin{array}{ccccc}1& 1& 1& [1]& 0\\ -2& 1& -1& [0]& -1\\ 0& 3& 1& [0]& 0\end{array}\right]$$
发现没有单位矩阵不能使用单纯形法于是采用大M法，原来矩阵有一行于是补两个人工变量凑成一个单位矩阵
$$A=\left[\begin{array}{ccccccc}1& 1& 1& [1]& 0& 0& 0\\ -2& 1& -1& [0]& -1& 1& 0\\ 0& 3& 1& [0]& 0& 0& 1\end{array}\right]$$
则原来的线性规划转化为：
$min{z}^{\prime }=3x_1-x_3+M{x}_6+M{x}_7$
$$s.t.=\{\begin{array}{c}{x}_1+x_2+x_3+x_5=4\\ \\ -2x_1+x_2-x_3-x_5+x_6=1\\ \\ 3x_2+x_3+x_7=9\\ \\ x_j\ge 0(j=1,...,7)\end{array}$$
解答过程如下：

3)两阶段法
第一步：继承了大M法,先将目标函数，变成人工变量相加，其中M取1
其他条件不变，用单纯刑法使得所有的${\partial }_j\ge 0$，并且C_B不含人工变量，求解如下：

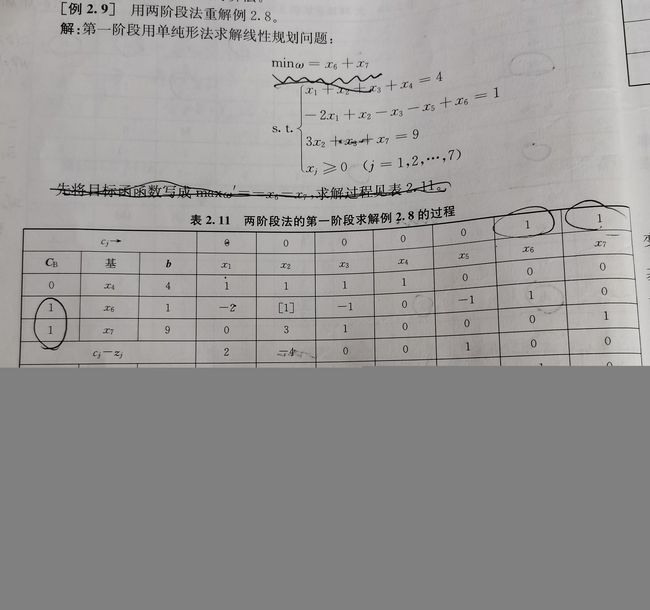
如果包含人工变量替换为其他变量
第二步：以第一阶段的最终单纯形表为基础，出去人工变量$x_6,x_7$及其系数列，只恢复基础变量的系数，其他不变，继续进行迭代，结果如下：

总结

练题是最重要的，多做多想。