C语言排序算法
排序的过程就是增加有序度,减少逆序度,最终达到满有序度
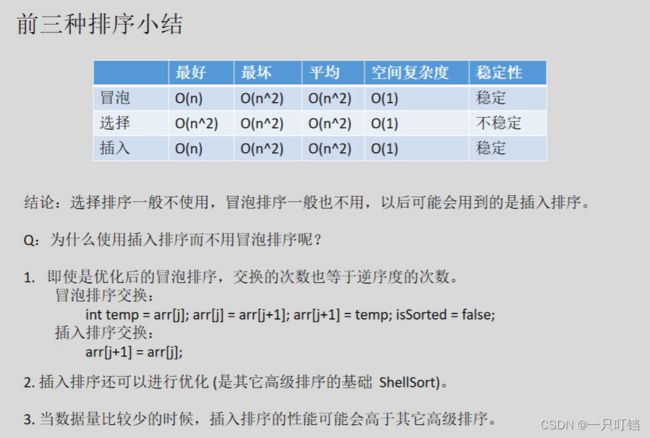
冒泡排序
#include 时间复杂度
最好情况:数组有序,O(n)
比较次数:n-1
交换次数:0
最坏情况:数组逆序,O(n^2)
比较次数:(n(n-1))/2
交换次数:(n(n-1))/2
稳定性:稳定
空间复杂度:O(1),原地排序
选择排序
表现稳定的排序算法之一,因为无论什么数据进去都是O(n^2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间
#include 时间复杂度
最好情况和最坏情况都是一样的,时间复杂度都是O(n)
比较次数:(n(n-1))/2
减缓次数:n-1
空间复杂度:O(1)
稳定性:不稳定(发生长距离交换)
插入排序
工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位ui,未最新元素提供插入空间,故名插入排序。
#include 时间复杂度
最好情况:原数组有序,O(n)
比较次数:n-1
交换次数“:0
最坏情况:原数组逆序,O(n^2)
比较次数:(n(n-1))/2
交换次数:(n(n-1))/2
当元素基本 有序时,性能非常好
空间复杂度:O(1),原地排序
稳定性:稳定
希尔排序
希尔排序又叫做缩小增量排序,是插入排序的改进版本,他是唯一打破时间复杂度O(n)的排序算法
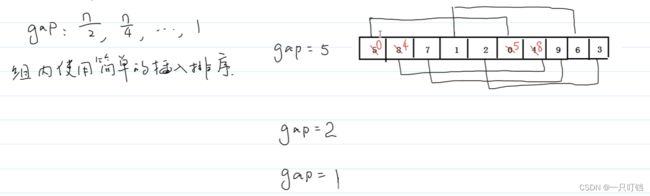
分组之后使用插入排序对每个分组进行排序
#include 时间复杂度:比O(n^2)小,和具体的gap序列相关
空间复杂度:O(1),原地排序
稳定性:不稳定(会发生长距离交换)
归并排序
归并排序基于分治思想,将数组拆分未元素更小的数组排序,排完序再合并小数组的结果
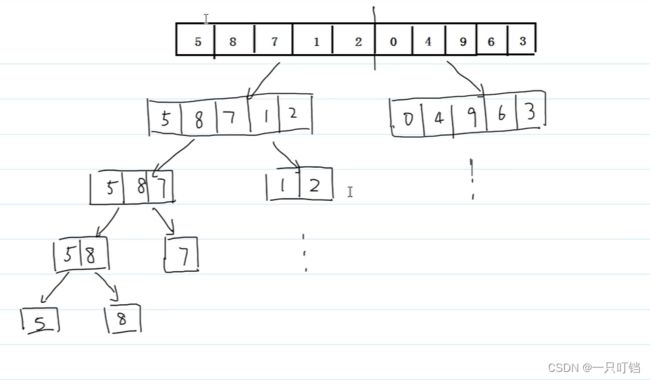
#include 时间复杂度:O(n^logbn)
空间复杂度:O(n)
稳定性:稳定
快速排序
快速排序可能是引用最广泛的派苏算法,快速排序流行多的原因是因为它实现简单,适用于各种不同的输入数据且在一般应用中比其他排序算法都要快很多,快速排序也是基于分治的思想。
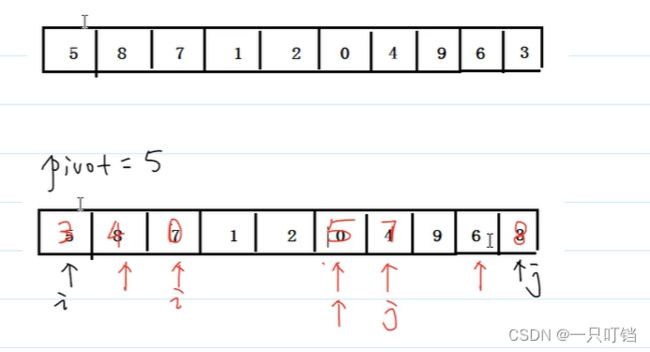
快速排序的步骤:
(1)选取基本值(pivot),一般选取第一个数据未基准值
(2)分区(partition),将所有比基准值小的数移动到基本值的左边,把所有比基准值大的数移动到基准值的右边
(3)对左边区间进行快速排序,对右边区间进行快速排序
#include 时间复杂度
最好情况:每次分区都分成大希奥相等的两份,O(nlogn)
最坏情况:每次基准值都位于最左边或者最右边,O(n^2)
空间复杂度:O(logn),递归的深度
稳定性:不稳定
改进策略:
(1)基准值的选取:随机选择,选择多个元素的中位数作为基准值
(2)分区操作优化,
(3)选择多个基准值
堆排序
二叉堆:
(1)大顶堆,根结点的键大于左右子树所有结点的键,并且左右子树都是大顶堆;
(2)小顶堆,根结点的键小于左右子树所有结点的键,并且左右子树都是小顶堆
堆排算法步骤:
(1)构大顶堆,找到第一个非叶子结点,从后往前构建大顶堆
(2)把堆顶元素和无序区的最后一个元素交换,无序区的长度减一
(3)把无序区重新调整成大顶堆
(4)重复(2)、(3)的操作,知道无序区的长度为0
#include