数据结构与算法教程,数据结构C语言版教程!(第二部分、线性表详解:数据结构线性表10分钟入门)九
第二部分、线性表详解:数据结构线性表10分钟入门
![]()
线性表,数据结构中最简单的一种存储结构,专门用于存储逻辑关系为"一对一"的数据。
线性表,基于数据在实际物理空间中的存储状态,又可细分为顺序表(顺序存储结构)和链表(链式存储结构)。
本章还会讲解顺序表和链表的结合体——静态链表,不仅如此,还会涉及循环链表、双向链表、双向循环链表等链式存储结构。
十七、如何判断单链表为有环链表?
循环链表一节,给大家详细地介绍了循环链表。在此基础上,本节带领大家讨论一个问题:如何判断一个单链表中有环?
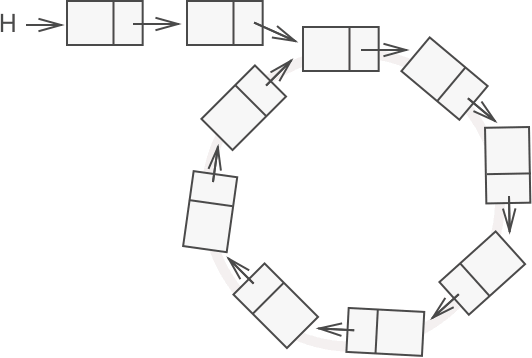
注意,有环链表并不一定就是循环链表。循环链表指的是“首尾相连”的单链表,而有环链表则指的是单链表中存在一个循环子链表,如图 1 所示。
图 1 有环链表示意图
图 1 所示就是一个有环链表,但并不是循环链表。
那么,如果给定一个单链表,如何判断其是否为有环链表呢?常用的判断方法有如下 2 种。
1) 最直接的实现思想就是:从给定链表的第一个节点开始遍历,每遍历至一个节点,都将其和所有的前驱节点进行比对,如果为同一个节点,则表明当前链表中有环;反之,如果遍历至链表最后一个节点,仍未找到相同的节点,则证明该链表中无环。
注意,如果一个单链表为有环链表,基于单链表中各节点有且仅有 1 个指针域的特性,则势必该链表是没有尾结点的(如图 1 所示)。换句话说,有环链表的遍历过程是无法自行结束的,需要使用 break 语句手动结束遍历。
基于上面的实现思想,下面设计了一个相应的实现函数:
//自定义 bool 类型
typedef enum bool
{
False=0,
True=1
}bool;
// H 为链表的表头
bool HaveRing(link * H) {
link * Htemp = H; /
/存储所遍历节点所有前驱节点的存储地址,64位环境下地址占 8 个字节,所以这里用 long long 类型
long long addr[20] = { 0 };
int length = 0, i = 0;
//逐个遍历链表中各个节点
while (Htemp) {
//依次将 Htemp 和 addr 数组中记录的已遍历的地址进行比对
for (i = 0; i < length; i++) {
//如果比对成功,则证明有环
if (Htemp == addr[i]) {
return True;
}
}
//比对不成功,则记录 Htemp 节点的存储地址
addr[length] = Htemp;
length++;
Htemp = Htemp->next;
}
return False;
}
如上所示,当函数的返回值为 True,表示该链表有环;反之若函数返回值为 False,表明链表中无环。显然,此实现方案的时间复杂度为O(。![]() )
)
2) 相比上一种实现方案,这里介绍一种时间复杂度为 O(n) 的算法。
该算法的实现思想需要借助一个论点,即在一个链表中,如果 2 个指针(假设为 H1 和 H2)都从表头开始遍历链表,其中 H1 每次移动 2 个节点的长度(H1 = H1->next->next),而 H2 每次移动 1 个节点的长度(H2 = H2->next),如果该链表为有环链表,则 H1、H2 最终必定会相等;反之,如果该链表中无环,则 H1、H2 永远不会相遇。
有关在有环链表中 H1 和 H2 必定会相遇的结论,假设有环链表中的环包含 n 个节点,则第一次遍历,H1 和 H2 相差 1 个节点;第二次遍历,H1 和 H2 相差 2 个节点;第三次遍历,H1 和 H2 相差 3 个节点...,最终经过多次遍历,H1 和 H2 会相差 n-1 个节点,此时就会在环中重合,此时 H1 和 H2 相等。
基于以上这个结论,我们可以轻松编写出对应的实现代码:
//H为链表的表头,该函数会返回一个枚举的 bool 类型数据
bool HaveRing(link * H) {
link * H1 = H->next;
link * H2 = H;
while (H1) {
if (H1 == H2) {
//链表中有环
return True;
} else {
H1 = H1->next;
if (!H1) {
//链表中无环
return False;
}
else
{
H1 = H1->next;
H2 = H2->next;
}
}
}
//链表中无环
return False;
}
和上一种实现代码一样,当函数返回 False 时,表明当前链表中无环;反之若返回 True,则表明该链表为有环链表。和第一种算法相比,本算法的时间复杂度为 O(n)。
十八、双向循环链表(C语言)详解
我们知道,单链表通过首尾连接可以构成单向循环链表,如图 1 所示:
图 1 单向循环链表示意图
同样,双向链表也可以进行首尾连接,构成双向循环链表。如图 2 所示:
图 2 双向循环链表示意图
当问题中涉及到需要 "循环往复" 地遍历表中数据时,就需要使用双向循环链表。例如,前面章节我们对约瑟夫环问题进行了研究,其实约瑟夫环问题有多种玩法,每次顺时针报数后,下一轮可以逆时针报数,然后再顺时针......一直到剩下最后一个人。解决这个问题就需要使用双向循环链表结构。
双向循环链表的创建
创建双向循环链表,只需在创建完成双向链表的基础上,将其首尾节点进行双向连接即可。
C 语言实现代码如下:
//创建双向循环链表
line* initLine(line * head){
head=(line*)malloc(sizeof(line));
head->prior=NULL;
head->next=NULL;
head->data=1;
line * list=head;
for (int i=2; i<=3; i++) {
line * body=(line*)malloc(sizeof(line));
body->prior=NULL;
body->next=NULL;
body->data=i;
list->next=body;
body->prior=list;
list=list->next;
}
//通过以上代码,已经创建好双线链表,接下来将链表的首尾节点进行双向连接
list->next=head;
head->prior=list;
return head;
}
通过向 main 函数中调用 initLine 函数,就可以成功创建一个存储有 {1,2,3} 数据的双向循环链表,其完整的 C 语言实现代码为:
#include
#include
typedef struct line{
struct line * prior;
int data;
struct line * next;
}line;
line* initLine(line * head);
void display(line * head);
int main() {
line * head=NULL;
head=initLine(head);
display(head);
return 0;
}
//创建双向循环链表
line* initLine(line * head){
head=(line*)malloc(sizeof(line));
head->prior=NULL;
head->next=NULL;
head->data=1;
line * list=head;
for (int i=2; i<=3; i++) {
line * body=(line*)malloc(sizeof(line));
body->prior=NULL;
body->next=NULL;
body->data=i;
list->next=body;
body->prior=list;
list=list->next;
}
//通过以上代码,已经创建好双线链表,接下来将链表的首尾节点进行双向连接
list->next=head;
head->prior=list;
return head;
}
//输出链表的功能函数
void display(line * head){ l
ine * temp=head;
//由于是循环链表,所以当遍历指针temp指向的下一个节点是head时,证明此时已经循环至链表的最后一个节点
while (temp->next!=head) {
if (temp->next==NULL) {
printf("%d\n",temp->data);
}else{
printf("%d->",temp->data);
}
temp=temp->next;
}
//输出循环链表中最后一个节点的值
printf("%d",temp->data);
}
程序输出结果如下:
1->2->3