Python 利用PYQT5设计基于RSA算法盲签名的匿名化电子支付系统设计与实现

基于RSA算法的盲签名算法

        David Chaum 于1982年提出盲签名的概念，并利用RSA算法设计了第一个盲签名方案. 该方案的安全性基于大整数分解问题

盲签名的步骤

1.密钥生成

签名者执行以下步骤生成密钥对:

①签名者选择两个大素数p,q， 计算n=pq， φ(n)=(p-1)(q-1);

②签名者选择两个大整数e,d, 满足ed =1 mod φ(n)， gcd(e, φ(n))= 1;

③签名者保存私钥(d,n)， 并公开公钥(e, n)和安全哈希函数H:{0,1}*→Zn*.

2.盲化

①用户选择随机数r∈R Zn*， 计算m' = re H(m) mod n，其中m是待签名的消息;

②用户将盲化的消息m'发送给签名者.

 3.签名

签名者计算σ' ≡ m' d  mod n ，并将 σ' 发送给用户。

4.去盲化

用户计算σ ≡ σ' r-1  mod n

r-1是盲化因子的逆元

 5.签名正确性验证

用户通过验证σe ≡ H(m) mod n

详细设计

我们为这个基于盲签名的匿名化电子支付系统设计了服务端（交易方）和用户端（被交易方）。和一个管理系统

1.密钥生成

        使用RSA模块的generate生成密钥对

# 生成 RSA 密钥对
def generate_rsa_key_pair():
    private_key = rsa.generate_private_key(
        public_exponent=65537,
        key_size=2048
    )
    public_key = private_key.public_key()
    return private_key, public_key

2.生成盲化因子

        使用secrets.randbits(1024)生成一个1024位的随机数，再用Miller-Rabin算法检查n是否是素数当n为素数的时候输出为盲化因子

def generate_blinding_factor():
    # 生成盲化因子（一个1024位的随机素数）
    while True:
        prime_candidate = secrets.randbits(1024)
        if is_prime(prime_candidate):
            return prime_candidate

def is_prime(n, k=5):
    # 用Miller-Rabin算法检查n是否是素数
    if n < 2: return False
    for p in [2,3,5,7,11,13,17,19,23,29]:
        if n % p == 0: return n == p
    s, d = 0, n - 1
    while d % 2 == 0:
        s, d = s + 1, d // 2
    for i in range(k):
        x = pow(secrets.randbelow(n-3) + 2, d, n)
        if x == 1 or x == n - 1: continue
        for r in range(s - 1):
            x = pow(x, 2, n)
            if x == n - 1: break
        else:
            return False
    return True

3.消息盲化

        发送者使用盲化因子 k 对原始消息 m 进行盲化操作，生成盲化后的消息 m'。公钥 e 和 n 是接收者的公钥，在进行盲化和解盲化操作时需要使用。m‘=mk^emod(n)

def blind_hide_msg(msg, factor, e, n):
    hide_msg = (msg * pow(factor, e, n)) % n
    return hide_msg

4.接收方签名

接收方计算s’=(m’)^d(mod n)并把计算后的签名值s’发送给发送方

def blind_signature(blind_msg, d, n):
    blind_sig = pow(blind_msg, d, n)
    return blind_sig

5.解盲

        签名者将签名值 s' 发送回给发送者。发送者使用盲化因子的逆元素和签名值 s1 结合起来计算原始消息 m 的数字签名 s。

def blind_retrieve_sig(blind_sig, factor, n):
    inverse = pow(factor, -1, n)
    signature = (blind_sig * inverse) % n
    return signature

6.验证盲签名 

         发送方计算接收方发送的s‘，并计算出原始的消息m的数字签名 s=s’k^−1(mod n) 与接收方计算的数字签名进行一个比较，如果相同接收方验证盲签名成功！ 用户通过验证s‘e ≡ H(m) mod n来验证盲签名

verification_result = pow(unblinded_signature2,e1,n1)

算法运行截图

完整算法代码

from cryptography.hazmat.primitives import serialization
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
import binascii
import secrets
import gmpy2
import hashlib
import random
from Crypto.Signature import pkcs1_15
from Crypto.Hash import SHA256
from Crypto.PublicKey import RSA
from Cryptodome.Util.number import inverse

def blind_hide_msg(msg, factor, e, n):
    hide_msg = (msg * pow(factor, e, n)) % n
    return hide_msg

def blind_signature(blind_msg, d, n):
    blind_sig = pow(blind_msg, d, n)
    return blind_sig


# 判断是否为素数
def is_prime(num):
    if num <= 1:
        return False
    for i in range(2, int(num**0.5) + 1):
        if num % i == 0:
            return False
    return True


def generate_blinding_factor():
    # 生成盲化因子（一个1024位的随机素数）
    while True:
        prime_candidate = secrets.randbits(1024)
        if is_prime(prime_candidate):
            return prime_candidate

def is_prime(n, k=5):
    # 用Miller-Rabin算法检查n是否是素数
    if n < 2: return False
    for p in [2,3,5,7,11,13,17,19,23,29]:
        if n % p == 0: return n == p
    s, d = 0, n - 1
    while d % 2 == 0:
        s, d = s + 1, d // 2
    for i in range(k):
        x = pow(secrets.randbelow(n-3) + 2, d, n)
        if x == 1 or x == n - 1: continue
        for r in range(s - 1):
            x = pow(x, 2, n)
            if x == n - 1: break
        else:
            return False
    return True

# 生成 RSA 密钥对
def generate_rsa_key_pair():
    private_key = rsa.generate_private_key(
        public_exponent=65537,
        key_size=2048
    )
    public_key = private_key.public_key()
    return private_key, public_key

# 保存密钥到文件
def save_key_to_file(key, filename):
    pem = key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.NoEncryption()
    )
    with open(filename, 'wb') as f:
        f.write(pem)

# 从文件中加载密钥
def load_key_from_file(filename):
    with open(filename, 'rb') as f:
        pem = f.read()
        key = serialization.load_pem_private_key(pem, password=None)
    return key

def blind_retrieve_sig(blind_sig, factor, n):
    inverse = pow(factor, -1, n)
    signature = (blind_sig * inverse) % n
    return signature


#--------------`--------------------------------------------------------------------------------
# 生成 RSA 密钥对
private_key, public_key = generate_rsa_key_pair()
bank_private_key, bank_public_key = generate_rsa_key_pair()

# 保存私钥到文件
private_key_file = "private_key.pem"
private_key_file2 = "bank_private_key.pem"
save_key_to_file(private_key, private_key_file)
save_key_to_file(bank_private_key,private_key_file2)
# 保存公钥到文件
public_key_file = "public_key.pem"
public_key_file2 = "bank_public_key.pem"
with open(public_key_file, 'wb') as f:
    f.write(public_key.public_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PublicFormat.SubjectPublicKeyInfo
    ))
with open(public_key_file2, 'wb') as f:
    f.write(public_key.public_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PublicFormat.SubjectPublicKeyInfo
    ))

# 从文件中加载密钥
loaded_private_key = load_key_from_file(private_key_file)
loaded_bank_private_key = load_key_from_file(private_key_file2)
loaded_public_key = serialization.load_pem_public_key(open(public_key_file, 'rb').read())
loaded_bank_public_key = serialization.load_pem_public_key(open(public_key_file2, 'rb').read())

# 从加载的密钥中提取模数 n、私钥指数 d 和公钥指数 e
n = loaded_private_key.private_numbers().public_numbers.n
d = loaded_private_key.private_numbers().d
e = loaded_public_key.public_numbers().e

# 从加载的密钥中提取模数 n、私钥指数 d 和公钥指数 e
n1 = loaded_bank_private_key.private_numbers().public_numbers.n
d1 = loaded_bank_private_key.private_numbers().d
e1 = loaded_bank_public_key.public_numbers().e

# 清除返回值对象，防止泄露信息
loaded_private_key = None
loaded_public_key = None

print("n:", n)
print("d:", d)
print("e:", e)
print("n1:", n1)
print("d1:", d1)
print("e1:", e1)



m =1234
# 生成盲化因子Alice选择一个随机数  k 作为盲化因子
k = generate_blinding_factor()
print("blinding factor",k)

#generate_blinding_factor()函数使用secrets.randbits(1024)生成一个随机的1024位素数作为盲化因子。
#is_prime()函数使用Miller-Rabin算法检查整数是否是素数。然后，blind_message()函数将盲化因子应用于消息，以生成盲化的消息和盲化因子的值。
#1.发送者使用盲化因子 k 对原始消息 m 进行盲化操作，生成盲化后的消息 m'。公钥 e 和 n 是接收者的公钥，在进行盲化和解盲化操作时需要使用。
m1 = blind_hide_msg(m,k, e1, n1)#盲化
print("盲化后的消息 m':",m1)
#发送者将盲化后的消息 m1 发送给签名者。

#2.签名者使用私钥对盲化后的消息 m1 进行解密操作，生成签名值 s1。 d1和n1是签名者银行的私钥
s1 = blind_signature(m1, d1, n1)
print("签名值 s'", s1)
real_sig = pow(m, d1, n1)
print("原签名 =", real_sig)



#3.签名者将签名值 s' 发送回给发送者。发送者使用盲化因子的逆元素和签名值 s1 结合起来计算原始消息 m 的数字签名 s。
unblinded_signature2=blind_retrieve_sig(s1,k, n1)
print("解盲后", unblinded_signature2)

if unblinded_signature2==real_sig:
    print("验证成功！！！！")
else:
    print("验证失败")

hash_value = hashlib.sha256(str(m).encode()).digest()
# 4验证数字签名
verification_result = pow(unblinded_signature2,e1,n1)
# 计算验证结果的哈希值
verification_bytes = verification_result.to_bytes((verification_result.bit_length() + 7) // 8, byteorder="big")
verification_hash = hashlib.sha256(verification_bytes).digest()
print("verification_hash",verification_hash)
print("unblinded_signature2",unblinded_signature2)
# 将哈希值转换为整数类型
hash_int = int.from_bytes(hash_value, byteorder="big")

# 检查验证结果是否与哈希值一致
if verification_result == m:
    print("数字签名验证通过")
else:
    print("数字签名验证失败")

系统测试

系统执行流程图

        本系统的执行过程如图所示。首先客户端用户查询要发送的对象，然后用户输入要盲化的金额、输入发送对象名、输入备注，然后使用密钥对金额进行盲化，并将这些信息作为盲化请求发送给服务端，服务端用户首先可以查看到用户发送过来的盲化请求，然后输入序号可以下载密钥，然后解密，再用密钥生成自己的签名值，发送给客户端用户，客户端用户接收到该签名值之后用密钥解盲。

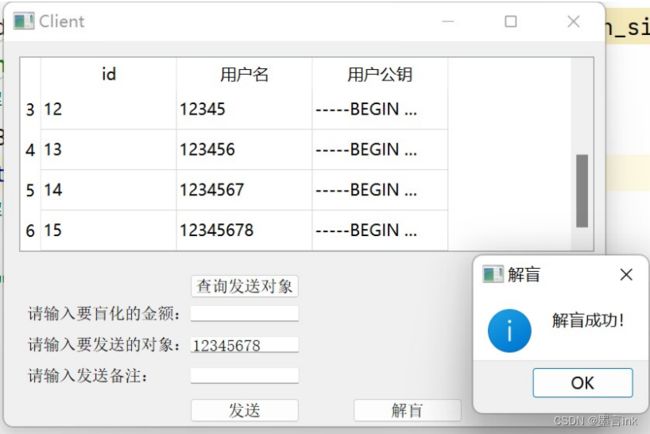
用户查询发送对象

客户端用户先点击按钮按钮查询可发送的对象。

用户发送信息

        用户输入要交易（盲化）的金额，输入要发送的对象名，输入备注，点击发送按钮将这些值以及盲化金额发送给交易方。

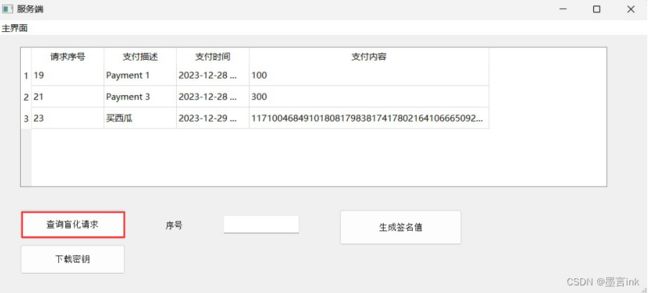
服务端（交易方）可以查询被交易方发过来的盲化请求。

下载用户公钥，交易方下载密钥。

 签名者验证发送方身份

服务端生成签名值

然后点击按钮将该值发送给客户端用户。

发送方接收到服务端返回的签名进行解盲

发送方解盲后发送给第三方，第三方验证签名

第三方验证签名

数据库设计 

数据表建立语句

验证签名表
CREATE TABLE `verify_sign` (
  `id` int NOT NULL AUTO_INCREMENT,
  `userfrom` varchar(255) DEFAULT NULL,
  `d` text,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=8 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci

用户信息表
CREATE TABLE `user_info` (
  `id` int NOT NULL AUTO_INCREMENT,
  `userfrom` varchar(255) DEFAULT NULL,
	`m` text,
  `k` text,
  `n` text,
	`e` text,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=2 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci
服务端盲签名回应表
CREATE TABLE `blind_response2` (
  `id` int NOT NULL AUTO_INCREMENT,
  `userfrom` varchar(255) DEFAULT NULL,
	`userto` varchar(255) DEFAULT NULL,
  `sign_sig` text,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=41 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci
客户端用户请求发送表
CREATE TABLE `blind_payrequest2` (
  `id` int NOT NULL AUTO_INCREMENT,
  `userfrom` varchar(255) DEFAULT NULL,
	`userto` varchar(255) DEFAULT NULL,
  `payment_description` varchar(255) DEFAULT NULL,
  `payment_time` datetime DEFAULT NULL,
  `payment_amount` text,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=19 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci
用户密钥表
CREATE TABLE `user_keys` (
  `id` int NOT NULL AUTO_INCREMENT,
  `user` varchar(255) DEFAULT NULL,
  `public_key` TEXT,
  `private_key` TEXT,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=10 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci