小白学习深度学习之(二)——softmax回归
softmax回归
- 什么是softmax回归
- 分类问题
- 网络架构
- 全连接层的参数开销
- softmax运算
- 图像分类数据集
- softmax回归的简洁实现
-
- 初始化模型参数
- 损失函数
- 优化算法
- 训练
什么是softmax回归
回归可以用于预测多少的问题,比如预测房屋被出售的价格,或者棒球队可能获胜的胜场数,又或者患者住院的天数。但是事实上,我们也对分类问题感兴趣:不是问“多少”,而是哪一个
分类问题
我们从一个图像分类问题开始。 假设每次输入是一个 2×2 的灰度图像。 我们可以用一个标量表示每个像素值,每个图像对应四个特征 1,2,3,4 。 此外,假设每个图像属于类别“猫”“鸡”和“狗”中的一个。
接下来,我们要选择如何表示标签。 我们有两个明显的选择:最直接的想法是选择 ∈{1,2,3} , 其中整数分别代表 {狗,猫,鸡} 。 这是在计算机上存储此类信息的有效方法。 如果类别间有一些自然顺序, 比如说我们试图预测 {婴儿,儿童,青少年,青年人,中年人,老年人} , 那么将这个问题转变为回归问题,并且保留这种格式是有意义的。
但是一般的分类问题并不与类别之间的自然顺序有关。 幸运的是,统计学家很早以前就发明了一种表示分类数据的简单方法:独热编码(one-hot encoding)。 独热编码是一个向量,它的分量和类别一样多。 类别对应的分量设置为1,其他所有分量设置为0。 在我们的例子中,标签 将是一个三维向量, 其中 (1,0,0) 对应于“猫”、 (0,1,0) 对应于“鸡”、 (0,0,1) 对应于“狗”:
y ∈ { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } . y \in \{(1, 0, 0), (0, 1, 0), (0, 0, 1)\}. y∈{(1,0,0),(0,1,0),(0,0,1)}.
网络架构
为了估计所有可能类别的条件概率,我们需要一个有多个输出的模型,每个类别对应一个输出。 为了解决线性模型的分类问题,我们需要和输出一样多的仿射函数(affine function)。 每个输出对应于它自己的仿射函数。 在我们的例子中,由于我们有4个特征和3个可能的输出类别, 我们将需要12个标量来表示权重(带下标的 ), 3个标量来表示偏置(带下标的 )。 下面我们为每个输入计算三个未规范化的预测(logit): 1 、 2 和 3 。
o 1 = x 1 w 11 + x 2 w 12 + x 3 w 13 + x 4 w 14 + b 1 , o 2 = x 1 w 21 + x 2 w 22 + x 3 w 23 + x 4 w 24 + b 2 , o 3 = x 1 w 31 + x 2 w 32 + x 3 w 33 + x 4 w 34 + b 3 . \begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\ o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\ o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3. \end{aligned} o1o2o3=x1w11+x2w12+x3w13+x4w14+b1,=x1w21+x2w22+x3w23+x4w24+b2,=x1w31+x2w32+x3w33+x4w34+b3.
与线性回归一样,softmax回归也是一个单层的神经网络。输出层也是全连接层
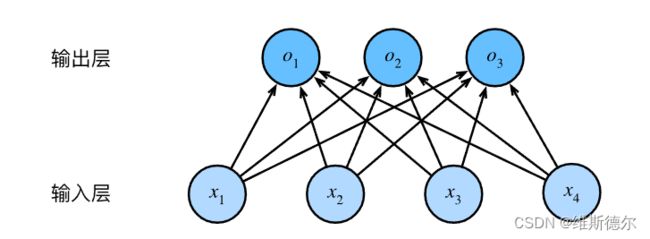
为了更简洁地表达模型,我们仍然使用线性代数符号。 通过向量形式表达为 =+ , 这是一种更适合数学和编写代码的形式。 由此,我们已经将所有权重放到一个 3×4 矩阵中。 对于给定数据样本的特征 , 我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置 得到的。
全连接层的参数开销
正如我们将在后续章节中看到的,在深度学习中,全连接层无处不在。 然而,顾名思义,全连接层是“完全”连接的,可能有很多可学习的参数。 具体来说,对于任何具有 个输入和 个输出的全连接层, 参数开销为 O ( d q ) \mathcal{O}(dq) O(dq) ,这个数字在实践中可能高得令人望而却步。 幸运的是,将 个输入转换为 个输出的成本可以减少到 O ( d q n ) \mathcal{O}(\frac{dq}{n}) O(ndq), 其中超参数 可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性 :cite:Zhang.Tay.Zhang.ea.2021。
softmax运算
现在我们将优化参数以最大化观测数据的概率。为了得到预测结果,我们将设置一个阈值,如选择具有最大概率的标签。
图像分类数据集
(MNIST数据集) (是图像分类中广泛使用的数据集之一,但作为基准数据集过于简单。 我们将使用类似但更复杂的Fashion-MNIST数据集)
softmax回归的简洁实现
我们发现(通过深度学习框架的高级API能够使实现) (softmax) 线性(回归变得更加容易)。 同样,通过深度学习框架的高级API也能更方便地实现softmax回归模型。 本节如在中一样, 继续使用Fashion-MNIST数据集,并保持批量大小为256
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
初始化模型参数
[softmax回归的输出层是一个全连接层]。 因此,为了实现我们的模型, 我们只需在Sequential中添加一个带有10个输出的全连接层。 同样,在这里Sequential并不是必要的, 但它是实现深度模型的基础。 我们仍然以均值0和标准差0.01随机初始化权重。
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状
#将张量全都变成一个二维的,只保留第一维,将剩下的都变成一个
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
损失函数
loss = nn.CrossEntropyLoss(reduction='none')#reduction不进行降维
优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
训练
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)