数模学习day08-拟合算法
这里拟合算法可以和差值算法对比
引入
插值和拟合的区别
与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟
合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所
有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。
插值算法中,得到的多项式f(x)要经过所有样本点。但是如果样本点太多,那
么这个多项式次数过高,会造成龙格现象。
尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更倾向于得到
一个确定的曲线,尽管这条曲线不能经过每一个样本点,但只要保证误差足够小即
可,这就是拟合的思想。(拟合的结果是得到一个确定的曲线)
小例子
拟合曲线
最小二乘法的集合解释
往往使用第二种定义,这也正是最小二乘的思想。
为什么不用四次方?
(1)避免极端数据对拟合曲线的影响。
(2)最小二乘法得到的结果和MLE极大似然估计一致。
不用奇数次方的原因:误差会正负相抵。
求解最小二乘法
Matlab求解最小二乘法
clear;clc
load data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法:模拟生成x和y的序列,比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b % k和b都是已知值
% plot(xx,yy,'-')
% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')
如何评价拟合的好坏
![]() 最接近一最好
最接近一最好
证明SST = SSE + SSR
"线性函数"的介绍
![]() 只能用于拟合函数是“线性函数”时,拟合结果的评价
只能用于拟合函数是“线性函数”时,拟合结果的评价
如何判断线性于参数的函数
在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不
能出现参数的复合函数形式。
计算拟合优度代码
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST注:mean()是求均值的函数。
曲线拟合工具箱
低版本的Matlab可以在命令窗口中直接输入”cftool”
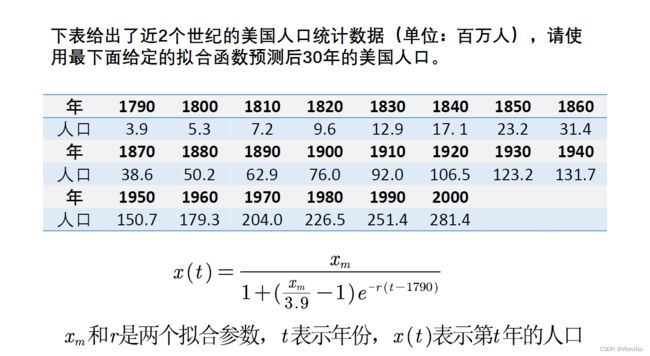
利用拟合工具箱预测美国人口
自己模拟数据进行演示
% (1)randi : 产生均匀分布的随机整数(i = int)
%产生一个1至10之间的随机整数矩阵,大小为2x5;
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵,大小为1x10;
s2 = randi([-5,5],1,10)
% (2) rand: 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵,大小为1x5;
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵,大小为1x5; % a + (b-a) * rand(1,5); 如:a,b = 2,5
s4= 2 + (5-2) * rand(1,5)
% (3)normrnd:产生正态分布的随机数
%产生一个均值为0,标准差(方差开根号)为2的正态分布的随机矩阵,大小为3x4;
s5 = normrnd(0,2,3,4)
% (4)roundn—任意位置四舍五入
% 0个位 1十位 2百位 -1小数点后一位
a = 3.1415
roundn(a,-2) % ans = 3.1400
roundn(a,2) % ans = 0
a =31415
roundn(a,2) % ans = 31400
roundn(5.5,0) %6
roundn(5.5,1) %10
clear;clc
x = rand(30,1) * 10; % x是0-10之间均匀分布的随机向量(30个样本)
y = 3 * exp(0.5*x) -5 + normrnd(0,1,30,1);
% cftool
优秀论文中 cftool 的运用
cftool的“sao”操作