CINTA第四次作业
文章目录
- 第七章习题
-
- 第二题
- 第三题
- 第六题
- 第八题
- 第八章习题
-
- 第一题
- 第三题
- 第五题
- 第九题
第七章习题
第二题
题目描述:群 Z 17 ∗ Z_{17}^{*} Z17∗有多少个生成元?已知3是其中一个生成元,请问9和10是否是生成元?
根据原根定理,群 Z 17 ∗ 有 ϕ ( 16 ) = 2 4 − 2 3 = 8 个生成元 根据原根定理,群Z_{17}^{*}有\phi(16)=2^{4}-2^{3}=8个生成元 根据原根定理,群Z17∗有ϕ(16)=24−23=8个生成元
群 Z 17 ∗ 的阶为 16 , 9 = 3 2 m o d 17 ∈ Z 17 ∗ , 但 g c d ( 2 , 16 ) = 2 ,所以 9 的阶为 8 ,不是生成元 群Z_{17}^{*}的阶为16,9=3^{2}mod\ 17\in Z_{17}^{*},但gcd(2,16)=2,所以9的阶为8,不是生成元 群Z17∗的阶为16,9=32mod 17∈Z17∗,但gcd(2,16)=2,所以9的阶为8,不是生成元
群 Z 17 ∗ 的阶为 16 , 10 = 3 3 m o d 17 ∈ Z 17 ∗ , 且 g c d ( 3 , 16 ) = 1 , 所以 10 的阶为 16 ,是生成元 群Z_{17}^{*}的阶为16,10=3^{3}mod\ 17\in Z_{17}^{*},且gcd(3,16)=1,所以10的阶为16,是生成元 群Z17∗的阶为16,10=33mod 17∈Z17∗,且gcd(3,16)=1,所以10的阶为16,是生成元
第三题
题目描述:p和q是两个不同的素数,请问 Z p q Z_{pq} Zpq有多少个生成元?r是任意正整数,请问 Z p r Z_{p^{r}} Zpr有多少个生成元?
Z p q 的生成元个数为 ϕ ( p q ) = ϕ ( p ) ϕ ( q ) = ( p − 1 ) ( q − 1 ) Z_{pq}的生成元个数为\phi(pq)=\phi(p)\phi(q)=(p-1)(q-1) Zpq的生成元个数为ϕ(pq)=ϕ(p)ϕ(q)=(p−1)(q−1)
Z p r 的生成元个数为 ϕ ( p r ) = p r − p r − 1 Z_{p^{r}}的生成元个数为\phi(p^{r})=p^{r}-p^{r-1} Zpr的生成元个数为ϕ(pr)=pr−pr−1
第六题
题目描述:证明:如果群G没有非平凡子群,则群G是循环群
上述命题等价于证明,如果群 G 只有平凡子群,则群 G 是循环群 上述命题等价于证明,如果群G只有平凡子群,则群G是循环群 上述命题等价于证明,如果群G只有平凡子群,则群G是循环群
当 G = { e } 时,显然群 G 是循环群 当G=\{e\}时,显然群G是循环群 当G={e}时,显然群G是循环群
当 G ≠ { e } 时,任取 g ∈ G 且 g ≠ e , < g > 是 G 的子群 当G\not = \{e\}时,任取g\in G且g\not = e,
因为 G 只有平凡子群 { e } 和 G 本身,显然 < g > ≠ { e } , 因此 < g > = G , G 是循环群 因为G只有平凡子群\{e\}和G本身,显然
所以,如果群 G 没有平凡子群,则群 G 是循环群 所以,如果群G没有平凡子群,则群G是循环群 所以,如果群G没有平凡子群,则群G是循环群
第八题
题目描述:证明:设G为任意群,且 g ∈ G g\in G g∈G。如果存在m,n ∈ Z \in Z ∈Z使得 g m = 1 g^{m}=1 gm=1且 g n = 1 g^{n}=1 gn=1,则 g d = 1 g^{d}=1 gd=1,其中d=gcd(m,n)
根据贝祖定理,存在 r , s ∈ Z , 使得 d = m r + n s 根据贝祖定理,存在r,s\in Z,使得d=mr+ns 根据贝祖定理,存在r,s∈Z,使得d=mr+ns
g d = g m r + n s = ( g m ) r ⋅ ( g n ) s = 1 g^{d}=g^{mr+ns}=(g^{m})^{r}·(g^{n})^{s}=1 gd=gmr+ns=(gm)r⋅(gn)s=1
即证得 即证得 即证得
( 之前也想写贝祖定理,但总感觉奇奇怪怪的 ) (之前也想写贝祖定理,但总感觉奇奇怪怪的) (之前也想写贝祖定理,但总感觉奇奇怪怪的)
第八章习题
第一题
题目描述:设G是群,H是G的子群。任取 g 1 , g 2 ∈ G g_{1},g_{2}\in G g1,g2∈G,则 g 1 H = g 2 H 当且仅当 g 1 − 1 g 2 ∈ H g_{1}H=g_{2}H当且仅当g_{1}^{-1}g_{2}\in H g1H=g2H当且仅当g1−1g2∈H
先证充分性:任取 h 1 , h 2 ∈ H , 有 g 1 h 1 = g 2 h 2 , 则 h 1 = g 1 − 1 g 2 h 2 , h 1 h 2 − 1 = g 1 − 1 g 2 , h 1 h 2 − 1 ∈ H , 因此 g 1 − 1 g 2 ∈ H 先证充分性:任取h_{1},h_{2}\in H,有g_{1}h_{1}=g_{2}h_{2},则h_{1}=g_{1}^{-1}g_{2}h_{2},h_{1}h_{2}^{-1}=g_{1}^{-1}g_{2},h_{1}h_{2}^{-1}\in H,因此g_{1}^{-1}g_{2}\in H 先证充分性:任取h1,h2∈H,有g1h1=g2h2,则h1=g1−1g2h2,h1h2−1=g1−1g2,h1h2−1∈H,因此g1−1g2∈H
再证必要性: e 为单位元,已知 g 1 − 1 g 2 ∈ H , 则 g 1 g 1 − 1 g 2 = g 2 = g 2 e ,即 g 1 H = g 2 H 再证必要性:e为单位元,已知g_{1}^{-1}g_{2}\in H,则g_{1}g_{1}^{-1}g_{2}=g_{2}=g_{2}e,即g_{1}H=g_{2}H 再证必要性:e为单位元,已知g1−1g2∈H,则g1g1−1g2=g2=g2e,即g1H=g2H
证得, g 1 H = g 2 H 当且仅当 g 1 − 1 g 2 ∈ H 证得,g_{1}H=g_{2}H当且仅当g_{1}^{-1}g_{2}\in H 证得,g1H=g2H当且仅当g1−1g2∈H
第三题
题目描述:如果G是群,H是群G的子群,且[G:H]=2,请证明对任意的 g ∈ G g\in G g∈G,gH=Hg
因为 [ G : H ] = 2 , 因此群 G 被划分成两个不相同的陪集 H 、 H ′ 因为[G:H]=2,因此群G被划分成两个不相同的陪集H、H' 因为[G:H]=2,因此群G被划分成两个不相同的陪集H、H′
若 g ∈ H , 根据封闭性, g 被 H 吸收, g H = H g = H 若g\in H,根据封闭性,g被H吸收,gH=Hg=H 若g∈H,根据封闭性,g被H吸收,gH=Hg=H
若 g ∈ H ′ , 有 g H ≠ H , H g ≠ H , 则 g H = H ′ , H g = H ′ , g H = H g = H ′ 若g\in H',有gH\not = H,Hg\not = H,则gH=H',Hg=H',gH=Hg=H' 若g∈H′,有gH=H,Hg=H,则gH=H′,Hg=H′,gH=Hg=H′
第五题
题目描述:设G是阶为pq的群,其中p和q是素数。请证明G的任意非平凡子群是循环群
根据拉格朗日定理, G 是有限群,对任意 g ∈ G , o r d ( g ) ∣ ∣ G ∣ , ∣ G ∣ = p q , 则 G 的任意非平凡子群 g , o r d ( g ) = p 或 o r d ( g ) = q 根据拉格朗日定理,G是有限群,对任意g\in G,ord(g)\ |\ |G|,|G|=pq,则G的任意非平凡子群g,ord(g)=p或ord(g)=q 根据拉格朗日定理,G是有限群,对任意g∈G,ord(g) ∣ ∣G∣,∣G∣=pq,则G的任意非平凡子群g,ord(g)=p或ord(g)=q
根据推论 8.2 知,素数有限群是循环群 根据推论8.2知,素数有限群是循环群 根据推论8.2知,素数有限群是循环群
即证得, G 的任意非平凡子群是循环群 即证得,G的任意非平凡子群是循环群 即证得,G的任意非平凡子群是循环群
第九题
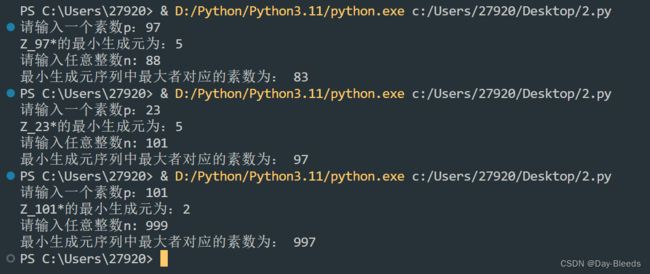
编程完成一下工作:对任意给定的一个素数p,求出 Z p ∗ Z_{p}^{*} Zp∗的最小生成元。任取一个整数n,对大于1小于n的所有素数p,求 Z p ∗ Z_{p}^{*} Zp∗的最小生成元,并求以上最小生成元集合中最大者所对应的素数p
参考了书上的一段代码
def prime_factor_list(p):
list = []
for i in range(2, p-1):
if (p-1) % i == 0:
list.append(i)
return list
def is_primitive_root(a, p):
flist = prime_factor_list(p)
for f in flist:
if pow(a, (p-1)//f, p) == 1:
return False
return True
def get_prime_list(n):
list = []
for i in range(2, n):
count = 0
for j in range(2, i):
if i % j != 0:
count += 0
else:
count += 1
if count == 0:
list.append(i)
return list
p = int(input("请输入一个素数p:"))
if p == 2:
print(f"Z_{p}*的最小生成元为:1")
else:
for i in range(1, p-1):
if is_primitive_root(i, p):
print(f"Z_{p}*的最小生成元为:{i}")
break
primitive_root = []
n = int(input("请输入任意整数n: "))
for i in get_prime_list(n):
if i == 2:
primitive_root.append(1)
else:
for j in range(1, i-1):
if is_primitive_root(j, i):
primitive_root.append(j)
break
max_primitive_root = min(primitive_root)
max_prime = []
if max_primitive_root == 1:
print("最小生成元序列中最大者对应的素数为:", max(get_prime_list(n)))
elif max_primitive_root > 1:
for i in get_prime_list(n):
for j in range(1, i-1):
if is_primitive_root(j, i):
max_prime.append(j)
break
print("最小生成元序列中最大者对应的素数为:", max_prime)