Atcoder Beginner Contest 335 （A - F 题）

A - 2023

Problem Statement

You are given a string $S$ consisting of lowercase English letters and digits.
$S$ is guaranteed to end with 2023.
Change the last character of $S$ to 4 and print the modified string.

Constraints

• $S$ is a string of length between $4$ and $100$, inclusive, consisting of lowercase English letters and digits.
• $S$ ends with 2023.

Input

The input is given from Standard Input in the following format:

$S$

Output

Print the answer.

Sample Input 1

hello2023

Sample Output 1

hello2024

Changing the last character of hello2023 to 4 yields hello2024.

Sample Input 2

worldtourfinals2023

Sample Output 2

worldtourfinals2024

Sample Input 3

2023

Sample Output 3

2024

$S$ is guaranteed to end with 2023, possibly being 2023 itself.

Sample Input 4

20232023

Sample Output 4

20232024

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	string S;

	cin >> S;

	int N = S.size();
	S = ' ' + S;

	S[N] = '4';

	S.erase(0, 1);
	cout << S << endl;

	return 0;
}

B - Tetrahedral Number

Problem Statement

You are given an integer $N$.

Print all triples of non-negative integers $(x,y,z)$ such that $x+y+z\le N$ in ascending lexicographical order.

What is lexicographical order for non-negative integer triples?

A triple of non-negative integers $(x,y,z)$ is said to be lexicographically smaller than $(x^{\prime },y^{\prime },z^{\prime })$ if and only if one of the following holds:

• $x<x^{\prime }$;
• $x=x^{\prime }$ and $y<y^{\prime }$;
• $x=x^{\prime }$ and $y=y^{\prime }$ and $z<z^{\prime }$.

Constraints

• $0\le N\le 21$
• $N$ is an integer.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print all triples of non-negative integers $(x,y,z)$ such that $x+y+z\le N$ in ascending lexicographical order, with $x,y,z$ separated by spaces, one triple per line.

Sample Input 1

3

Sample Output 1

0 0 0
0 0 1
0 0 2
0 0 3
0 1 0
0 1 1
0 1 2
0 2 0
0 2 1
0 3 0
1 0 0
1 0 1
1 0 2
1 1 0
1 1 1
1 2 0
2 0 0
2 0 1
2 1 0
3 0 0

Sample Input 2

4

Sample Output 2

0 0 0
0 0 1
0 0 2
0 0 3
0 0 4
0 1 0
0 1 1
0 1 2
0 1 3
0 2 0
0 2 1
0 2 2
0 3 0
0 3 1
0 4 0
1 0 0
1 0 1
1 0 2
1 0 3
1 1 0
1 1 1
1 1 2
1 2 0
1 2 1
1 3 0
2 0 0
2 0 1
2 0 2
2 1 0
2 1 1
2 2 0
3 0 0
3 0 1
3 1 0
4 0 0

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int N;

	cin >> N;

	for (int X = 0; X <= N; X ++)
		for (int Y = 0; Y <= N; Y ++)
			for (int Z = 0; Z <= N; Z ++)
				if (X + Y + Z <= N)
					cout << X << " " << Y << " " << Z << endl;

	return 0;
}

C - Loong Tracking

Problem Statement

Takahashi has created a game where the player controls a dragon on a coordinate plane.

The dragon consists of $N$ parts numbered $1$ to $N$, with part $1$ being called the head.

Initially, part $i$ is located at the coordinates $(i,0)$. Process $Q$ queries as follows.

• 1 C: Move the head by $1$ in direction $C$. Here, $C$ is one of R, L, U, and D, which represent the positive $x$-direction, negative $x$-direction, positive $y$-direction, and negative $y$-direction, respectively. Each part other than the head moves to follow the part in front of it. That is, part $i$ $(2\le i\le N)$ moves to the coordinates where part $i-1$ was before the move.
• 2 p: Find the coordinates of part $p$.

Constraints

• $2\le N\le 10^6$
• $1\le Q\le 2\times 10^5$
• For the first type of query, $C$ is one of R, L, U, and D.
• For the second type of query, $1\le p\le N$.
• All numerical input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $Q$
${\mathrm{query}}_1$
$⋮$
${\mathrm{query}}_Q$

Each query is in one of the following two formats:

$1$ $C$

$2$ $p$

Output

Print $q$ lines, where $q$ is the number of queries of the second type.
The $i$-th line should contain $x$ and $y$ separated by a space, where $(x,y)$ are the answer to the $i$-th such query.

Sample Input 1

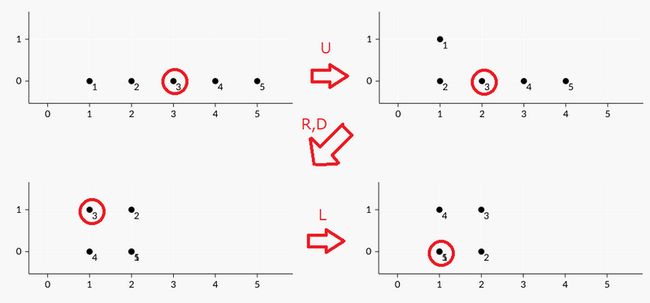
5 9
2 3
1 U
2 3
1 R
1 D
2 3
1 L
2 1
2 5

Sample Output 1

113

The integers that can be expressed as the sum of exactly three repunits are $3,13,23,33,113,\dots$ in ascending order. For example, $113$ can be expressed as $113=1+1+111$.
Note that the three repunits do not have to be distinct.

Sample Input 2

3 0
2 0
1 1
1 0
1 0

At each time when processing the second type of query, the parts are at the following positions:

Note that multiple parts may exist at the same coordinates.

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 2e5 + 10;

int N, Q;
int X[SIZE], Y[SIZE];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> Q;

	int i = 0;
	X[0] = 1, Y[0] = 0;
	while (Q --)
	{
		int op, P;
		char T;

		cin >> op;

		if (op == 1)
		{
			cin >> T;
			i ++;
			if (T == 'R') X[i] = X[i - 1] + 1, Y[i] = Y[i - 1];
			else if (T == 'U') Y[i] = Y[i - 1] + 1, X[i] = X[i - 1];
			else if (T == 'L') X[i] = X[i - 1] - 1, Y[i] = Y[i - 1];
			else Y[i] = Y[i - 1] - 1, X[i] = X[i - 1];
		}
		else
		{
			cin >> P;
			if (i < P) cout << P - i << " " << 0 << endl;
			else cout << X[i - P + 1] << " " << Y[i - P + 1] << endl;
		}
	}

	return 0;
}

D - Loong and Takahashi

Problem Statement

There is a grid with $N$ rows and $N$ columns, where $N$ is an odd number at most $45$.

Let $(i,j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left.

In this grid, you will place Takahashi and a dragon consisting of $N^2-1$ parts numbered $1$ to $N^2-1$ in such a way that satisfies the following conditions:

• Takahashi must be placed at the center of the grid, that is, in cell $(\frac{N+1}{2},\frac{N+1}{2})$.
• Except for the cell where Takahashi is, exactly one dragon part must be placed in each cell.
• For every integer $x$ satisfying $2\le x\le N^2-1$, the dragon part $x$ must be placed in a cell adjacent by an edge to the cell containing part $x-1$.
  • Cells $(i,j)$ and $(k,l)$ are said to be adjacent by an edge if and only if $|i-k|+|j-l|=1$.

Print one way to arrange the parts to satisfy the conditions. It is guaranteed that there is at least one arrangement that satisfies the conditions.

Constraints

• $3\le N\le 45$
• $N$ is odd.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print $N$ lines.
The $i$-th line should contain $X_{i,1},\dots ,X_{i,N}$ separated by spaces, where $X_{i,j}$ is T when placing Takahashi in cell $(i,j)$ and $x$ when placing part $x$ there.

Sample Input 1

5

Sample Output 1

1 2 3 4 5
16 17 18 19 6
15 24 T 20 7
14 23 22 21 8
13 12 11 10 9

The following output also satisfies all the conditions and is correct.

9 10 11 14 15
8 7 12 13 16
5 6 T 18 17
4 3 24 19 20 
1 2 23 22 21

On the other hand, the following outputs are incorrect for the reasons given.

Takahashi is not at the center.

1 2 3 4 5
10 9 8 7 6
11 12 13 14 15
20 19 18 17 16
21 22 23 24 T

The cells containing parts $23$ and $24$ are not adjacent by an edge.

1 2 3 4 5
10 9 8 7 6
11 12 24 22 23
14 13 T 21 20
15 16 17 18 19

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 50;

int N;
int Result[SIZE][SIZE];
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N;

	int X = 1, Y = 1, Sd = 0;
	for (int i = 1; i <= N; i ++)
		Result[0][i] = 1e18, Result[N + 1][i] = 1e18, Result[i][0] = 1e18, Result[i][N + 1] = 1e18;
	for (int i = 1; i <= N * N - 1; i ++)
	{
		Result[X][Y] = i;
		if (Result[X + dx[Sd]][Y + dy[Sd]]) Sd = (Sd + 1) % 4;
		X += dx[Sd], Y += dy[Sd];
	}

	for (int i = 1; i <= N; i ++)
	{
		for (int j = 1; j <= N; j ++)
			if ((1 + N >> 1) == i && i == j)
				cout << "T ";
			else
				cout << Result[i][j] << " ";
		cout << endl;
	}

	return 0;
}

E - Non-Decreasing Colorful Path

Problem Statement

There is a connected undirected graph with $N$ vertices and $M$ edges, where the $i$-th edge connects vertex $U_i$ and vertex $V_i$ bidirectionally.
Each vertex has an integer written on it, with integer $A_v$ written on vertex $v$.

For a simple path from vertex $1$ to vertex $N$ (a path that does not pass through the same vertex multiple times), the score is determined as follows:

• Let $S$ be the sequence of integers written on the vertices along the path, listed in the order they are visited.
• If $S$ is not non-decreasing, the score of that path is $0$.
• Otherwise, the score is the number of distinct integers in $S$.

Find the path from vertex $1$ to vertex $N$ with the highest score among all simple paths and print that score.

What does it mean for $S$ to be non-decreasing? A sequence $S=(S_1,S_2,\dots ,S_l)$ of length $l$ is said to be non-decreasing if and only if $S_i\le S_{i+1}$ for all integers $1\le i<l$.

Constraints

• All input values are integers.
• $2\le N\le 2\times 10^5$
• $N-1\le M\le 2\times 10^5$
• $1\le A_i\le 2\times 10^5$
• The graph is connected.
• $1\le U_i<V_i\le N$
• $(U_i,V_i)\ne (U_j,V_j)$ if $i\ne j$.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$A_1$ $A_2$ $\dots$ $A_N$
$U_1$ $V_1$
$U_2$ $V_2$
$⋮$
$U_M$ $V_M$

Output

Print the answer as an integer.

Sample Input 1

5 6
10 20 30 40 50
1 2
1 3
2 5
3 4
3 5
4 5

Sample Output 1

4

The path $1\to 3\to 4\to 5$ has $S=(10,30,40,50)$ for a score of $4$, which is the maximum.

Sample Input 2

4 5
1 10 11 4
1 2
1 3
2 3
2 4
3 4

Sample Output 2

0

There is no simple path from vertex $1$ to vertex $N$ such that $S$ is non-decreasing. In this case, the maximum score is $0$.

Sample Input 3

10 12
1 2 3 3 4 4 4 6 5 7
1 3
2 9
3 4
5 6
1 2
8 9
4 5
8 10
7 10
4 6
2 8
6 7

Sample Output 3

5

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef pair<int, PII> PIII;

const int SIZE = 2e5 + 10;

int N, M, A[SIZE], P[SIZE], F[SIZE];
std::vector<PIII> Edge;
std::vector<int> G[SIZE];
int Vis[SIZE];
vector<int> Point;

int Find(int x)
{
	if (P[x] != x) P[x] = Find(P[x]);
	return P[x];
}

void BFS()
{
	queue<int> Q;
	Q.push(Find(1));

	while (Q.size())
	{
		int u = Q.front();
		Q.pop();

		if (Vis[u]) continue;
		Vis[u] = 1;
		Point.push_back(u);

		for (auto c : G[u])
			Q.push(c);
	}
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> M;

	for (int i = 1; i <= N; i ++)
		cin >> A[i], P[i] = i;

	int u, v;
	for (int i = 1; i <= M; i ++)
	{
		cin >> u >> v;
		if (A[u] > A[v]) swap(u, v);
		if (A[u] == A[v]) P[Find(v)] = Find(u);
		else Edge.push_back({A[u], {u, v}});
	}

	// for (auto c : Edge)
	// 	G[Find(c.first)].push_back(Find(c.second));

	// BFS();

	sort(Edge.begin(), Edge.end());

	memset(F, -0x3f, sizeof F);
	F[Find(1)] = 1;
	for (auto c : Edge)
	{
		int u = Find(c.second.first), v = Find(c.second.second);
		F[v] = max(F[v], F[u] + 1);
	}

	cout << max(0ll, F[Find(N)]) << endl;

	return 0;
}

F - Hop Sugoroku

Problem Statement

There is a row of $N$ squares labeled $1,2,\dots ,N$ and a sequence $A=(A_1,A_2,\dots ,A_N)$ of length $N$.
Initially, square $1$ is painted black, the other $N-1$ squares are painted white, and a piece is placed on square $1$.

You may repeat the following operation any number of times, possibly zero:

• When the piece is on square $i$, choose a positive integer $x$ and move the piece to square $i+A_i\times x$.
  • Here, you cannot make a move with $i+A_i\times x>N$.
• Then, paint the square $i+A_i\times x$ black.

Find the number of possible sets of squares that can be painted black at the end of the operations, modulo $998244353$.

Constraints

• All input values are integers.
• $1\le N\le 2\times 10^5$
• $1\le A_i\le 2\times 10^5$

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $A_2$ $\dots$ $A_N$

Output

Print the answer as an integer.

Sample Input 1

5
1 2 3 1 1

Sample Output 1

8

There are eight possible sets of squares painted black:

• Square $1$
• Squares $1,2$
• Squares $1,2,4$
• Squares $1,2,4,5$
• Squares $1,3$
• Squares $1,4$
• Squares $1,4,5$
• Squares $1,5$

Sample Input 2

1
200000

Sample Output 2

1

Sample Input 3

40
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

Sample Output 3

721419738

Be sure to find the number modulo $998244353$.

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 2e5 + 10, SIZE2 = 450, MOD = 998244353;

int N;
int A[SIZE];
int F[SIZE], G[SIZE2][SIZE2];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N;

	for (int i = 1; i <= N; i ++)
		cin >> A[i];

	F[1] = 1;
	int B = sqrt(N) + 1;
	for (int i = 1; i <= N; i ++)
	{
		for (int j = 1; j <= B; j ++)
			F[i] = (F[i] + G[j][i % j]) % MOD;
		if (A[i] > B)
			for (int j = i + A[i]; j <= N; j += A[i])
				F[j] = (F[j] + F[i]) % MOD;
		else
			G[A[i]][i % A[i]] = (G[A[i]][i % A[i]] + F[i]) % MOD;
	}

	int Result = 0;
	for (int i = 1; i <= N; i ++)
		Result = (Result + F[i]) % MOD;

	cout << Result << endl;

	return 0;
}

视频题解

Atcoder Beginner Contest 335 讲解（A - F题）

---

最后祝大家早日