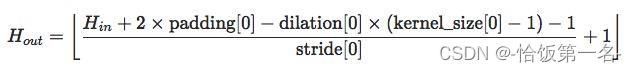nn网络层-卷积层

一、1d/2d/3d Convolution

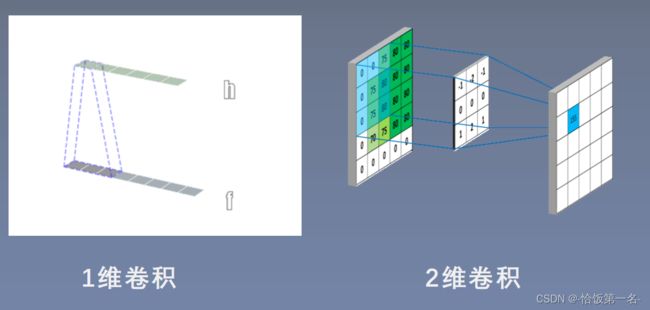
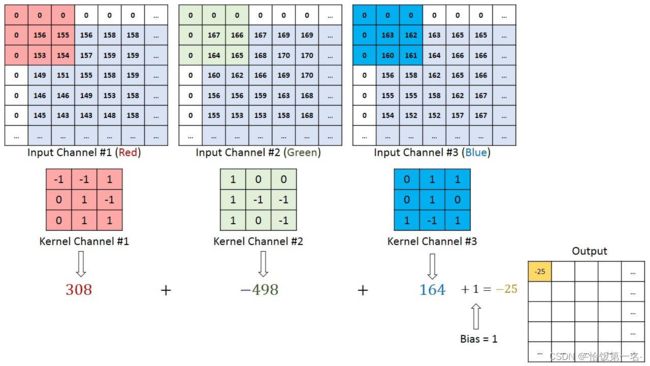
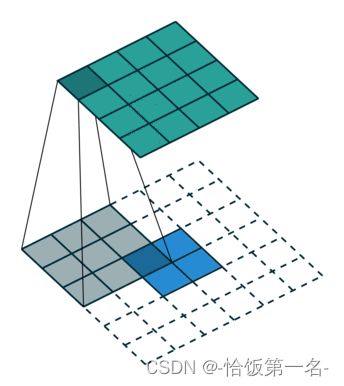
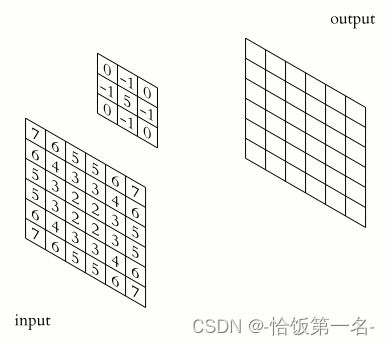
• 卷积运算：卷积核在输入信号（图像）上滑动，相应位置上进行乘加
• 卷积核：又称为滤波器，过滤器，可认为是某种模式，某种特征。
• 卷积过程类似于用一个模版去图像上寻找与它相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取

AlexNet卷积核可视化，发现卷积核学习到的是边缘，条纹，色彩这一些细节模式

卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积

二、nn.Conv2d

nn.Conv2d是PyTorch中用于进行二维卷积操作的类。它可以对多个二维信号（如图像）进行二维卷积操作。

nn.Conv2d的主要参数如下：

• in_channels：输入通道数，即输入信号的深度（或通道数）。
• out_channels：输出通道数，即卷积核的个数，也可以理解为卷积操作后得到的特征图的深度。
• kernel_size：卷积核的尺寸，可以是一个整数或一个元组，表示卷积核的高度和宽度。
• stride：步长，表示卷积核在输入信号上滑动的步长，默认为1。
• padding：填充个数，可以是一个整数或一个元组，表示在输入信号的周围填充的行数和列数，默认为0。
• dilation：空洞卷积的大小，表示卷积核中的元素之间的间隔，默认为1。
• groups：分组卷积设置，用于将输入和输出通道分组，默认为1，表示不分组。
• bias：是否使用偏置项，默认为True。
• padding_mode：填充模式，用于指定填充的方式，默认为’zeros’，表示用0进行填充。
  下面是nn.Conv2d的典型使用示例：

import torch
import torch.nn as nn
# 创建一个输入张量
input_tensor = torch.randn(1, 3, 32, 32)  # 输入通道数为3，大小为32x32的图像
# 创建一个卷积层
conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=1)
# 对输入张量进行卷积操作
output = conv_layer(input_tensor)

在上述示例中，我们首先创建了一个大小为1x3x32x32的输入张量，表示一个通道数为3、大小为32x32的图像。然后，我们创建了一个卷积层conv_layer，其中输入通道数为3，输出通道数为64，卷积核尺寸为3x3，步长为1，填充个数为1。最后，我们将输入张量传入卷积层进行卷积操作，得到输出张量output。

尺寸计算

完整版的二维卷积尺寸计算公式如下：

输出尺寸 = floor((输入尺寸 + 2 * 填充个数 - 卷积核尺寸) / 步长) + 1

其中，

• 输出尺寸是指卷积操作后得到的特征图的尺寸。
• 输入尺寸是指输入信号（如图像）的尺寸。
• 填充个数是指在输入信号的周围填充的行数和列数。
• 卷积核尺寸是指卷积核的高度和宽度。
• 步长是指卷积核在输入信号上滑动的步长。

这个公式可以用来计算卷积操作后得到的特征图的尺寸。

简化版：

简化版的二维卷积尺寸计算公式是在完整版的基础上进行了简化，假设填充个数为0，步长为1，即没有填充且卷积核每次滑动一个像素。这样，简化版的尺寸计算公式可以简化为：
输出尺寸 = 输入尺寸 - 卷积核尺寸 + 1

这个简化版的公式适用于常见的卷积操作情况，但在实际应用中，可能会根据具体需求进行填充和步长的设置，因此完整版的尺寸计算公式更加通用。

卷积维度：

一般情况下，卷积核在几个维度上滑动，就是几维卷积

三、转置卷积

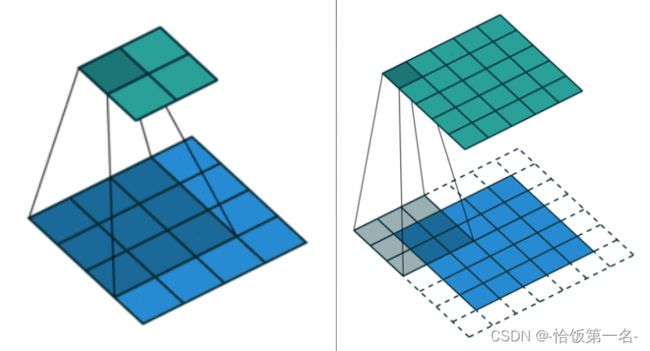
转置卷积又称为反卷积(Deconvolution)和部分跨越卷积(Fractionally-strided Convolution) ，用于对图像进行上采样(UpSample)

为什么称为转置卷积？
假设图像尺寸为4 * 4，卷积核为3 * 3，padding=0，stride=1

---

nn.ConvTranspose2d

nn.ConvTranspose2d是PyTorch中用于实现转置卷积的函数。它可以用来进行上采样操作，将输入特征图的尺寸增大。

该函数的主要参数如下：

• in_channels：输入通道数，指定输入特征图的通道数。
• out_channels：输出通道数，指定输出特征图的通道数。
• kernel_size：卷积核尺寸，指定卷积核的大小。
• stride：步长，指定卷积核在输入特征图上滑动的步长。
• padding：填充个数，指定在输入特征图周围添加的填充像素数。
• output_padding：输出填充个数，指定在输出特征图周围添加的填充像素数。
• groups：分组卷积设置，指定将输入通道和输出通道分成几组进行卷积操作。
• bias：是否使用偏置项。
• dilation：空洞卷积大小，指定卷积核中的元素之间的间距。
• padding_mode：填充模式，指定填充的方式，常用的有’zeros’和’reflection’。

例如，使用nn.ConvTranspose2d可以创建一个转置卷积层的实例：

import torch.nn as nn

# 创建一个转置卷积层的实例
conv_transpose = nn.ConvTranspose2d(in_channels=3, out_channels=64, kernel_size=3, stride=2, padding=1)

这样就创建了一个输入通道数为3，输出通道数为64的转置卷积层，卷积核大小为3x3，步长为2，填充个数为1。

转置卷积

转置卷积是一种用于实现上采样的操作，可以将输入特征图的尺寸增大。在转置卷积中，输出特征图的大小可以通过以下公式计算：

简化版：

out_size = (in_size - 1) * stride + kernel_size

完整版：

out_size = (in_size - 1) * stride - 2 * padding + dilation * (kernel_size - 1) + output_padding + 1

其中，

• in_size：输入特征图的尺寸。
• stride：步长，指定卷积核在输入特征图上滑动的步长。
• kernel_size：卷积核尺寸，指定卷积核的大小。
• padding：填充个数，指定在输入特征图周围添加的填充像素数。
• dilation：空洞卷积大小，指定卷积核中的元素之间的间距。
• output_padding：输出填充个数，指定在输出特征图周围添加的填充像素数。

这些公式可以用来计算转置卷积操作后输出特征图的尺寸。需要注意的是，由于转置卷积的操作涉及到填充和步长等参数，因此输出特征图的尺寸可能与输入特征图的尺寸不完全一致。

此外，您提到了棋盘效应（Checkerboard Artifacts）。这是在转置卷积中常见的一种伪影现象，可能导致生成的图像出现棋盘状的格子状伪影。为了减少棋盘效应，可以采用一些技巧，例如使用更大的步长、更小的卷积核尺寸、更大的填充等。