【信号处理】参数化重采样时频变换（PRTF变换）附matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

内容介绍

信号处理是数字信号处理领域中的一个重要分支，它涉及到对信号进行分析、处理和提取信息的技术和方法。参数化重采样时频变换（PRTF变换）是信号处理中的一种重要技术，它可以用于对信号进行时频分析，从而更好地理解信号的特性和行为。

许多信号包含多个具有时变瞬时频率 (IF) 的分量，这些分量具有共同的轨迹趋势，例如机械振动信号、语音信号和生物医学信号。为了分析此类信号并实现高时频分辨率，本文提出了一种称为参数化重采样时频变换（PRTF变换）的方法。采用一般参数化时频变换（GPTF变换）的思想，我们使用参数化核来表示重采样函数，并进一步构造时变和时不变重采样算子来消除中频变化并重新定位中频位置。这些算子可以同时提高时频表示（TFR）中多个分量的能量集中度。

PRTF变换是一种基于参数化重采样的时频变换方法，它可以将信号从时间域转换到时频域，从而揭示出信号在不同频率和时间上的特性。与传统的傅立叶变换方法相比，PRTF变换能够更好地处理非平稳信号，并且具有更好的时间和频率分辨率。

在进行PRTF变换时，首先需要对信号进行参数化重采样，这意味着将信号按照一定的规则进行重采样，以便在时频域上进行分析。参数化重采样可以根据信号的特性和需求进行不同的处理，比如对信号进行插值、滤波或者变换。通过参数化重采样，可以更好地准确表示信号在时频域上的特性，从而为后续的时频分析奠定基础。

在进行PRTF变换时，还需要选择合适的时频分析方法，比如短时傅立叶变换、小波变换等。这些方法可以根据信号的特性和需求进行选择，以便更好地揭示出信号在不同频率和时间上的特性。通过PRTF变换，可以更好地理解信号的频谱特性、时域特性和时频特性，从而为信号的分析和处理提供更多的信息和方法。

总之，参数化重采样时频变换（PRTF变换）是信号处理中的一种重要技术，它可以用于对信号进行时频分析，从而更好地理解信号的特性和行为。通过PRTF变换，可以更好地揭示出信号在不同频率和时间上的特性，为信号的分析和处理提供更多的信息和方法。希望本文能够对PRTF变换的理解和应用有所帮助，也希望能够为信号处理领域的发展和应用提供一些思路和方法。

部分代码

function [Spec,f] = STFT(Sig,SampFreq,N,WinLen);​% Calculating the Short Time Fourier Transform%%     Sig       : the signal to be analyzed%    SampFreq    : sampling frequency %        N       : the number of frequency bins %  WinLen       : the length of window used to locate the signal in time.​if (isreal(Sig))Sig = hilbert(Sig);end​SigLen = length(Sig);​​WinLen = ceil(WinLen / 2) * 2;t = linspace(-1,1,WinLen)';% sigma = 0.28;% WinFun = (pi*sigma^2)^(-1/4)*exp((-t.^2)/2/(sigma^2));WinFun = exp(log(0.005) * t.^2 );WinFun = WinFun / norm(WinFun);Lh = (WinLen - 1)/2; ​Spec = zeros(N,SigLen) ;  ​for iLoop = 1:SigLen,        tau = -min([round(N/2)-1,Lh,iLoop-1]):min([round(N/2)-1,Lh,SigLen-iLoop]);    temp = floor(iLoop + tau);    temp1 = floor(Lh+1+tau);    rSig = Sig(temp);​    rSig = rSig .* conj(WinFun(temp1));    Spec(1:length(rSig),iLoop) = rSig;end​​Spec = fft(Spec); Spec = abs(Spec);Spec = Spec(1:round(end/2)+1,:);[nLevel, ~] = size(Spec);f = [0:nLevel-1]/nLevel * SampFreq/2;  % frequency  in TF plane?​

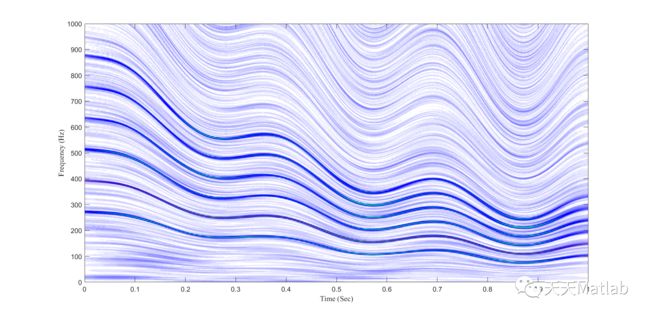
⛳️ 运行结果

参考文献

T. Li, Z. Peng, H. Xu and Q. He, "Parameterized domain mapping for order tracking of rotating machinery," in IEEE Transactions on Industrial Electronics, 2022, doi: 10.1109/TIE.2022.3201311

部分理论引用网络文献，若有侵权联系博主删除

 关注我领取海量matlab电子书和数学建模资料

 私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合