【字符加解密】基于RSA算法实现明文字符串加解密附Matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

内容介绍

字符加解密是计算机安全领域中的重要问题之一。在网络通信和数据传输过程中，为了保护数据的安全性，常常需要对明文进行加密，然后在接收端进行解密。RSA算法作为一种非对称加密算法，被广泛应用于信息安全领域。本文将介绍基于RSA算法实现明文字符串加解密的方法。

首先，我们需要了解RSA算法的原理。RSA算法是由三位数学家Rivest、Shamir和Adleman于1977年提出的，它基于大数分解的困难性来实现加密。RSA算法的关键在于生成一对公钥和私钥，其中公钥用于加密数据，私钥用于解密数据。公钥是由两个大素数的乘积组成，私钥则是这两个大素数的乘法逆元。RSA算法的加密过程是将明文字符串转换为数字，然后利用公钥进行加密；解密过程则是利用私钥对密文进行解密，得到原始的明文字符串。

接下来，我们将介绍如何基于RSA算法实现明文字符串的加解密。首先，我们需要生成一对公钥和私钥。这可以通过选择两个大素数p和q，然后计算它们的乘积n=pq。接着选择一个与(p-1)(q-1)互质的整数e作为公钥，再计算出与e关于(p-1)*(q-1)的乘法逆元d作为私钥。这样就得到了一对公钥(e, n)和私钥(d, n)。

接下来，我们可以利用生成的公钥对明文字符串进行加密。首先，将明文字符串转换为数字，然后利用公钥中的e和n进行加密运算，得到密文。解密过程则是利用私钥中的d和n进行解密运算，得到原始的明文字符串。

在实际应用中，RSA算法可以用于保护网络通信的安全性，例如在HTTPS协议中使用RSA算法对数据进行加密，以保护用户的隐私信息。此外，RSA算法还可以用于数字签名和身份认证等场景，以确保数据的完整性和真实性。

总之，基于RSA算法实现明文字符串加解密是一种非常有效的加密方法，它可以保护数据的安全性，防止数据被恶意篡改和窃取。在信息安全领域中，RSA算法将继续发挥重要作用，为网络通信和数据传输提供更加可靠的保护。

部分代码

%%  清空环境变量warning off             % 关闭报警信息close all               % 关闭开启的图窗clear                   % 清空变量clc                     % 清空命令行​%%  导入数据res = xlsread('数据集.xlsx');​%%  划分训练集和测试集temp = randperm(357);​P_train = res(temp(1: 240), 1: 12)';T_train = res(temp(1: 240), 13)';M = size(P_train, 2);​P_test = res(temp(241: end), 1: 12)';T_test = res(temp(241: end), 13)';N = size(P_test, 2);​%%  数据归一化[p_train, ps_input] = mapminmax(P_train, 0, 1);p_test  = mapminmax('apply', P_test, ps_input);t_train = ind2vec(T_train);t_test  = ind2vec(T_test );

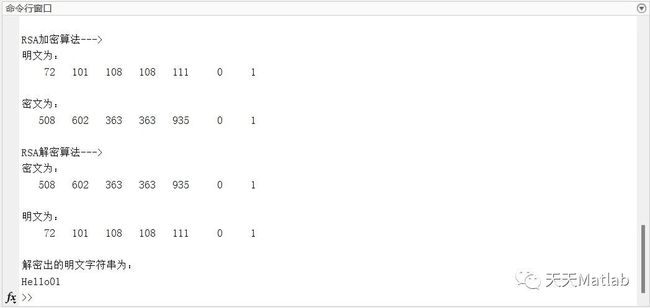
⛳️ 运行结果

参考文献

[1] 郭慧波.基于异步微流水线的RSA加解密算法研究与实现[D].广西民族大学[2023-12-11].DOI:CNKI:CDMD:2.1018.136770.

[2] 王涛,王旭辉,康晓凤.RSA数据加解密算法的研究及其Delphi实现[J].软件导刊, 2012, 11(2):2.DOI:CNKI:SUN:RJDK.0.2012-02-013.

部分理论引用网络文献，若有侵权联系博主删除

 关注我领取海量matlab电子书和数学建模资料

 私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合