【复习】人工智能 第六章 搜索求解策略（又多又难）

在求解一个问题时，涉及到两个方面：

（1）该问题的表示

（2）相对合适的求解方法：由于绝大多数需要人工智能方法求解的问题缺乏直接求解的方法，因此，搜索为一种求解问题的一般方法。

另外如果真的想拿下这一章，还是走一下ppt或书上的八数码的对应的每一种情况，不至于纸上谈兵。

一、搜索中需要解决的基本问题：

（1）是否能找到解。

（2）解是否是 最佳解。

（3）时间与空间复杂性如何。

（4）是否 终止运行 或 陷入一个死循环

二、状态空间图（重点）

问题的状态空间是一个表示该问题的全部可能状态及其变迁的有向图。

问题求解过程就是寻求图的某一路径的问题，实际上是一个搜索过程。

状态空间四元组：（S ，O ，S0 ，G）  

S ：状态集合。      

O ：操作算子的集合。  

S0 ：包含问题的初始状态是S的非空子集。

G ：若干具体状态或满足某些性质的路径信息描述        

例：

W：猴子的水平位置

Y：箱子的水平位置

x：当猴子在箱子顶上时取x=1;否则取x=0

z：当猴子摘到香蕉时取z=1；否则取z=0

初始和目标状态为：

初始状态：(a,b,0,0)

目标状态：(c,c,1,1)

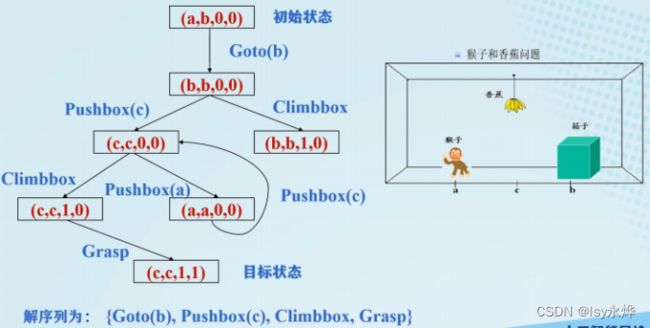
三、一般图搜索算法（了解即可）

符号说明，由于搜索是为了寻找初始节点到目标节点的路径，所以在搜索过程中就得随时记录搜索轨迹。

S-初始状态节点

G-搜索图

OPEN表 —— 存放 还没有扩展过 的全部节点

CLOSE —— 存放 已被扩展 的全部节点

MOVE-FIRST(OPEN) —— 取OPEN表首的节点作为当前要被扩展的节点n，同时将节点n移至CLOSE表

建立指向父节点的指针，并加入OPEN表；必须记住从目标返回的路径 — 每个表示状态的节点结构中必须有指向父节点的指针。

（其实就是不断生成新节点，在这个过程中，让新节点的指针指向自己的父亲）

带回溯策略的搜索：

一条路走到头，若它遇到不可解结点就回溯到路径中最近的父结点上，类似后面的深度优先，直到找到最终解。

(1) PS（path states）表：保存当前搜索路径上的状态。

(2) NPS（new path states）表：新的路径状态表。它包含了等待搜索的状态，其后裔状态还未被搜索到，即未被生成扩展 。

(3) NSS（no solvable states）表：不可解状态集，列出了找不到解题路径的状态。如果在搜索中扩展出的状态是它的元素，则可立即将之排除，不再继续。

四、盲目搜索（重点）

盲目即没有提示，分宽度优先和深度优先。

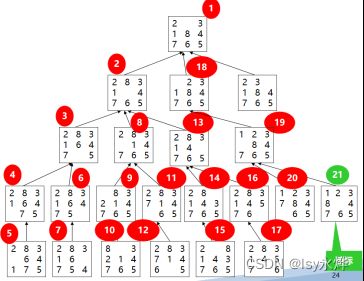
八数码问题（按中间那个空格有上下左右四个操作来走，不然按数字走太麻烦）：

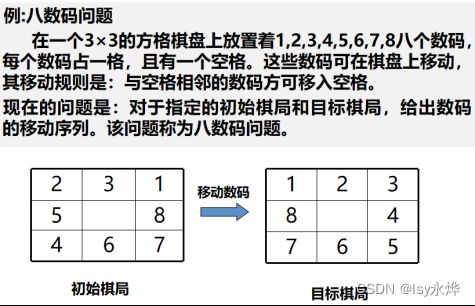
宽度优先就是把一个层级的父节点可以产生的下一级节点全部罗列出来，当然这样也就代表计算量有时候非常庞大，算也算不完。

搜索效率低，但是用宽度优先搜索总可以找到目标节点，而且总能找到最短路径。

用的是队列

深度优先就是一条路走到底，然后返回上一个父节点，找另外一条路再走到底，然后就是返回上上一个父节点再走到底。

但是若不加深度限制，可能沿着一条路线无限制地扩展下去，

所以得加深度界限，然后如果这个界限不够，再加一点再继续这个过程。

采用的是栈，栈就是乌鸦喝水的瓶子，先进后出。

五、启发式策略

给计算机一个提示，即启发式信息。

如下井字棋，给它一个提示信息——先下中间，这样它就先下中间了，少走了十年弯路！

必须要强调的是怎么算结束，遇到重复了的那条路就相当于结束了。

1.启发信息

分类：

a.陈述性启发信息

b.过程性启发信息

c.控制性启发信息

2.估价函数

f(n) = g(n) + h(n)

h（x） ：启发函数，有利于搜索纵向发展，提高搜索效率，但影响完备性。

g（x） ：代价函数，有利于搜索横向发展，提高搜索的完备性，但影响搜索效率。

估价函数f(n)：从初始结点经过 n结点 到达 目的结点 的路径的最小代价估计值，估计待搜索结点的“有希望”程度，并依次排序（在open表中）。

在f(n)中，g(n) 的比重越大，越倾向于宽度优先搜索方式，而 h(n) 的比重越大，表示启发性能越强。

 f（x）是初始节点S0到达节点x处已付出的代价与 节点x 到达目标节点Sg 的接近程度估计值总和，是 g（x）与 h（x）的折中。

3.极大极小分析法

还是跟上面一样，要用到树状图。

其中对称的按一种情况来算。

就是算每个节点的分数，类似与学习成绩，学大学好。

怎么算就拿井字棋为例，假设我们用的是“X”，那就是该状态下X的获胜情况减去O的获胜情况，得出来的值就是估价函数f(n)，但是根据后面来看这应该是h（n），最后找到一条路径，其中每一个节点的值都是最大的，那就是解。

至于为什么是最大的，是因为我肯定想大优势获胜，所以取大的值，想象一下机器人为了赢，已经算到你下的每一种情况后，它要做的针对手段。

倒推值：

但在实际情况中，都是先算子节点的哪几种情况的值，然后取最小值算作父节点的分数。

（与取最小值，或取最大值），然后一步步倒退父节点。

但是很明显，效率太低。所以又出现了α-β剪枝技术。

字面意思，减掉不用的，即一边推节点是什么样，一边算分数，直接把分数小的舍掉，这样就少算了很多差的结果，从而节约了机器开销, 提高了搜索效率。

六、A和A*寻路算法（重中之重，超级大题）

A和A*寻路算法都是寻找最优解的算法。

【估价函数f(n)=g(n)+h(n) 】

n —— 搜索图G中的节点；

f(n) —— G中从s经n到ng，估计的最小路径代价；

g(n) —— G中从s到n，目前实际的路径代价；

h(n) —— 从n到ng，估计的最小路径代价；

h(n)值 —— 依赖于启发式知识加以计算；

h(n)称为启发式函数，这个不是固定的，得根据具体情况设置，类似上面最大最小方法里面的分数，选择的参数h(n)越准确，到时候这个f(n)计算的也越nb。

1.A算法

类似极大极小算法在计算机的应用。

A算法的设计与一般图搜索相同，划分为二个阶段：

（1）初始化

建立只包含初始状态节点s的搜索图G:={s}

OPEN:={s}

CLOSE:={}

（2）搜索循环

MOVE-FIRST(OPEN) —— 取出OPEN表首的节点n 。

需要注意的是：对每个子节点ni，计算f(n,ni) = g(n,ni) + h(ni)，也就是n到ni的当前实际花费，和n到ni的最短路径花费。

途中不断将指针进行修改，就是比大小，哪个父节点短，就把指针指向这个父节点。

（3）八数码

对于我们熟悉的八数码问题，就可以将g(n)设置成深度（就是深度优先的第几层），然后关键的h（n）就可以设置成 当前 不在目标位置 的数量。

到时候算出来的新节点中还没来及算的放到open表中（可以详细深度优先一条路先走到黑），然后算过的放到close表中，close里面放的就是当前的推算过程的过程顺序，如果最后算出来最终结果，那这个就是一个解。

（4）搜索算法的可采纳性

就是能算出来解的，就是称该算法具有可采纳性，如，宽度优先的搜索算法是可采纳的，只是搜索效率不高。

那么A算法的可采纳性——定义f*(n) = g*(n) + h*(n)

n-搜索图G中最短解答路径的节点；

f*(n) —— s经节点n到ng的最短解答路径的路径代价；

g*(n) —— 该路径前段（从s到n）的路径代价；

h*(n) —— 该路径后段（从n到ng）的路径代价；

这里面看似跟原来的一样，但带了*之后就只表示最短路径那一条路，即最开始那个图。

也就是说若g(n)=g*(n)、h(n)=h*(n)，则搜索过程中，每次都是正确选择，也不扩展任何无关的节点。

h(n)尽可能靠近h*(n) ——A算法的关键。

下面简单说一下八数码（A算法）怎么提升可采纳性：

很简单，g(n)肯定变不了，那就变h(n)，原来h(n)是不在位的数字个数，那如果改成错位数字的最小移动距离和，是不是就变快了。

答案是肯定的，毕竟都这么问了。

2.A*搜索算法

为了更好的理解A*算法，先看一下深度、广度优先搜索算法。

（1）深度优先搜索，用俗话说就是不见棺材不回头。算法会朝一个方向进发，直到遇到边界或者障碍物，才回溯。

优点：

a.实现简单

缺点：

a.路径可能不是最优解；

b.寻路时间比较长。

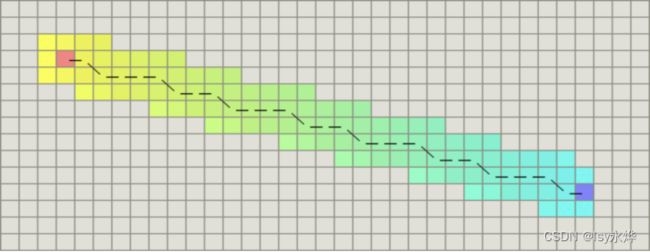
（2）广度优先搜索，这个用形象的比喻，就像是地震波，从起点向外辐射，直到找到目标点。

优点：

a.简单。代码也就几十行；

b.路径能找到最优解；

缺点：

a.算法遍历的结点很多

（3）最佳优先搜索

在一些情况下，如果我们可以预先计算出每个节点到终点的距离，则我们可以利用这个信息更快的到达终点。

但这种算法也存在缺点：

如果起点和终点之间存在障碍物，则最佳优先算法找到的很可能不是最短路径。

而 A*算法就是吸取这些算法（不止这两种）的优点，然后运用在电脑中：

广度优先搜索一层层的扩展，虽然让它找到了最优的路线，但是它却走完了绝大多数格子才找到我们的目标点。也就是，它只关注了当前扩展点和出发点的关系，而忽略了当前点和目标点的距离。而最佳优先搜索只关注了从当前节点到目标节点的路径，虽然有可能找到问题的解，但很可能不是最优解。所以A*算法实际上是综合上面这些算法的特点于一身的，即关注已经走过的节点的代价，又关注将来要走节点的代价。

A*算法通过下面这个函数来计算每个节点的优先级。

f(n) = g(n) + h(n)

f(n) —— 节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。

g(n) —— 节点n距离起点的代价。

h(n) —— 节点n距离终点的预计代价，这也就是A*算法的启发函数。

A*算法就是选择估计值最小（一般是最小的）继续走。

接下来有两个问题需要解决：

1、估算函数h(M)怎么样去计算？

对于网格形式的图，常见的距离计算公式有这么几种（注意每个点的四周）：

① 如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离。

② 如果图形中允许朝八个方向移动，则可以使用对角距离。

③ 如果图形中允许朝任何方向移动，则可以使用欧几里得距离。

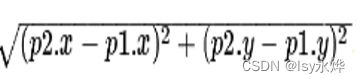
2、对于不同的估算函数h(M)来讲，对于我们的搜索结果会有什么样的影响？

（1） 当估算的距离h = 实际距离h'时，也就是每次扩展的那个点我们都准确的知道如果选它以后所得的路径距离是多少，这样我们就不用乱选了，每次都选最小的那个，一路下去，肯定就是最优的解，而且基本不用扩展其他的点

（2）如果估算距离h < 实际距离h'时，我们到最后一定能找到一条最短路径，但是有可能会经过很多无效的点。极端情况，当h==0的时候，最终的距离函数就变成：

f(M)=g(M)+h(M)   => f(M)=g(M)+0   => f(M)=g(M)

此时A*演变成Dijkstra（广度优先搜索）算法，这保证能找到最短路径，它只考虑和起始点的距离关系，毫无启发而言。h(n)越小，A*扩展的结点越多，运行就得越慢。

（3）如果估算距离h》实际距离h'时，有可能就很快找到一条通往目的地的路径，但是却不一定是最优的解。在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

怎么样的启发式算法是A*算法 ？

一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是：

      1、搜索树上存在着从起始点到终了点的最优路径。

      2、问题域是有限的。

      3、所有结点的子结点的搜索代价值>0。

      4、h(n)=