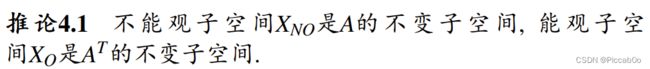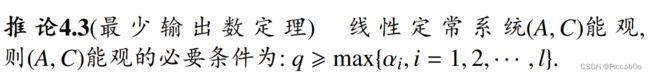【现代控制理论笔记】——第四章：能观性分析

现代控制理论

第四章

说明：

本章主要对系统的能观性进行分析，先给出了能观性的定义，进而引出了能观/不能观子空间，推出了能观性判据和能观性指数；针对不完全能观的系统，也对能观性分解进行了分析。这些都与系统能控性的分析具有一致性，这是因为系统复合对偶性原理。最后，给出了离散时间系统的能观性分析判定方法。

1. 能观性的定义

由系统的状态空间描述，可以得到系统的运动特性：

$x(t)=e^{At}x(0)+{\int }_0^t{e}^{A(t-\tau )}Bu(\tau )d\tau .$

可以看出，当输入给定时，系统的运动特性完全取决于初始状态。那么如何在已知输入输出的前提下，得到初始状态$x_0$便是待解决的问题。

对于一般情况，

$x(t)=e^{A(t-t_0)}x(t_0)+{\int }_{t_0}^t{e}^{A(t-\tau )}Bu(\tau )d\tau$

其输出响应为：

$y(t)=Cx(t)+Du(t)$

由于输入输出都假定已知，因此定义：

$\bar{y}=y-C{\int }_{t_0}^t{e}^{A(t-\tau )}Bu(\tau )d\tau -Du(t)$

$=C{e}^{A(t-t_0)}{x}_0$

能观性问题转变为$x_0$能不能由一一对应，进一步可以视作零输入系统：

$$\begin{gathered} \dot{x}=Ax \\ y=Cx \end{gathered}$$

输出唯一确定$x_0$的问题。

表示为：

若$x_0$为不能观测状态，当$t\in [t_0,T]$，有：

$y=C{e}^{A(t-t_0)}{x}_0\equiv 0$

2. 不能观子空间与能观子空间

不能观子空间$X_{NO}$的正交余空间称为能观子空间$X_O$。

不能观子空间：

上式取转置可得任一不可观状态$\alpha$与矩阵正交，因此有：

还可以推出：

3. 能观性判据

→Gram矩阵判据：

→秩判据：

→PBH判据：

→Jordan标准型判据：

可以推出：y为q维输出

→极点任意配置：

$(A,C)$能观等价于$(A^T,C^T)$能控

4. 能观性指数

对于能观性矩阵$Q_O$，定义：

Q k = [ C C A ⋮ C A k − 1 ] Q_k=\begin{bmatrix}C\\CA\\\vdots\\CA^{k-1}\end{bmatrix} Qk​= ​CCA⋮CAk−1​ ​

当k从1增加至v时，若$rank{Q}_v=Q_O=n$，则称v为能观性指数。

估计公式为：输出q维，rankC=m

$\frac{n}{q}⩽\nu ⩽n-m+1$

5. 能观性分解

对于能观性，也有类似的分解过程。

由：

取$Q_O$中m个线性无关的行，记作$H_1$，再取n-m个与之线性无关的行向量，记作$H_2$

令$T=[H_1;H_2]$，其为非奇异的。又记$T^{-1}=[T_1,T_2]$，由$T{T}^{-1}=I$得：

$H_1{T}_2=0$

这说明$T_2$各列属于$X_{NO}$，因此可以做等价变换：

$\begin{array}{rl}& \text{A}=TA{T}^{-1}\\ & =\left[\begin{array}{c}{H}_1\\ H_2\end{array}\right]A\left[\begin{array}{cc}{T}_1& T_2\end{array}\right]\\ & =\left[\begin{array}{cc}{H}_{1}A{T}_1& 0\\ H_{2}A{T}_1& H_{2}A{T}_2\end{array}\right]\triangleq \left[\begin{array}{cc}{A}_{11}& 0\\ A_{21}& A_{22}\end{array}\right],\\ & \hat{B}\text{= TB}\\ & =\left[\begin{array}{c}{H}_{1}B\\ H_{2}B\end{array}\right]\triangleq \left[\begin{array}{c}{B}_1\\ B_2\end{array}\right],\\ & \hat{C}=C{T}^{-1}\\ & =\left[\begin{array}{cc}C{T}_1& C{T}_2\end{array}\right]\\ & =\left[\begin{array}{cc}C{T}_1& 0\end{array}\right]\triangleq \left[\begin{array}{cc}{C}_1& 0\end{array}\right].\end{array}$

6. 单输入单输出系统的能观规范型：

其中，

Q = [ e 1 e 2 ⋮ e n ] = [ 1 α n − 1 ⋯ α 1 ⋱ ⋱ ⋮ ⋱ α n − 1 1 ] [ c A n − 1 c A n − 2 ⋮ c ] Q=\begin{bmatrix}e_1\\e_2\\\vdots\\e_n\end{bmatrix}=\begin{bmatrix}1&\alpha_{n-1}&\cdots&\alpha_1\\&\ddots&\ddots&\vdots\\&&\ddots&\alpha_{n-1}\\&&&1\end{bmatrix}\begin{bmatrix}cA^{n-1}\\cA^{n-2}\\\vdots\\c\end{bmatrix} Q= ​e1​e2​⋮en​​ ​= ​1​αn−1​⋱​⋯⋱⋱​α1​⋮αn−1​1​ ​ ​cAn−1cAn−2⋮c​ ​

注意：

这里能控标准型是$b_c=[0;0;...;1]$，对应的是$b_c=P^{-1}B$

而能观标准型是$c_o=[0;0;...;1]$，对应的是$c_o=C{Q}^{-1}$

注意能观标准型系统矩阵和能控标准型系统矩阵的异同

7. 对偶原理

结合前述能控性分析部分，我们发现能控性和能观性的分析在形式上很接近，这是由于系统的对偶原理导致的。

对偶原理指明了系统的控制问题和估计问题的内在联系。

定义：

若$(A_1,B_1,C_1)$和$(A_2,B_2,C_2)$两系统满足：

$A_1^T=-A_2,B_1^T=C_2,C_1^T=B_2$

则称两系统互为对偶系统。

有：

这说明$(A,C)$的能观性即是$(A^T,C^T)$的能控性。

8. 线性定常离散系统的能观性：

对于系统：

$\begin{array}{rl}x(k+1)& =Gx(k)\\ y(k)& =Cx(k)\end{array}$

线性定常连续时间系统离散化后的能观性：

离散后的系统能观，则离散前的系统一定能观。