冒泡排序，插入排序，选择排序和二分（折半）查找

冒泡排序的原理：

为了更深入地理解冒泡排序的操作步骤，我们现在看一下冒泡排序的原理。

首先我们肯定有一个数组，里面存放着待排序的元素列表，我们如果需要把比较大的元素排在前面，把小的元素排在后面，那么需要从尾到头开始下面的比较操作：

1. 从尾部开始比较相邻的两个元素，如果尾部的元素比前面的大，就交换两个元素的位置。
2. 往前对每个相邻的元素都做这样的比较、交换操作，这样到数组头部时，第 1 个元素会成为最大的元素。
3. 重新从尾部开始第 1、2 步的操作，除了在这之前头部已经排好的元素。
4. 继续对越来越少的数据进行比较、交换操作，直到没有可比较的数据为止，排序完成。

注意，看完了这里的操作步骤，我们可以想一下，如果从头到尾进行操作是否可以？当然不可以，不过这样可以完成从小到大的排序。

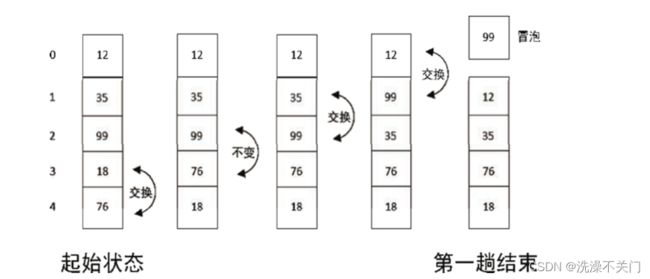
假如我们要把 12、35、99、18、76 这 5 个数从大到小进行排序，那么数越大，越需要把它放在前面。冒泡排序的思想就是在每次遍历一遍未排序的数列之后，将一个数据元素浮上去（也就是排好了一个数据）。

我们从后开始遍历，首先比较 18 和 76，发现 76 比 18 大，就把两个数交换顺序，得到 12、35、99、76、18；接着比较 76 和 99，发现 76 比 99 小，所以不用交换顺序；接着比较 99 和 35，发现 99 比 35 大，交换顺序；接着比较 99 和 12，发现 99 比 12 大，交换顺序。最终第 1 趟排序的结果变成了 99、12、35、76、18，排序的过程如图所示。 

​​

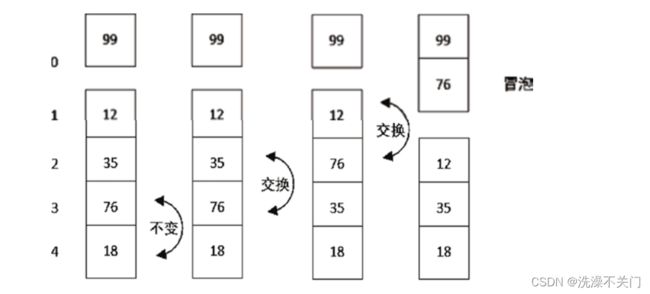
经过第 1 趟排序，我们已经找到了最大的元素，接下来的第 2 趟排序就只对剩下的 4 个元素排序。第 2 趟排序的过程示例如图 2 所示。

经过第 2 趟排序，结果为 99、76、12、35、18。接下来应该进行第 3 趟排序了，剩下的元素不多，比较次数也在减少。

第3趟排序的结果应该是 99、76、35、12、18，接下来第 4 趟排序的结果是 99、76、35、18、12，经过 4 趟排序之后，只剩一个 12 需要排序了，这时已经没有可比较的元素了，所以排序完成。
 

冒泡排序实现（从大到小）：

public void sort() {
        int length = array.length;
        if (length > 0) {
            for (int i = length - 1; i > 0; i--) {
                for (int j = length - 1; j > length - 1 - i ; j--) {
                    if (array[j] > array[j - 1]) {
                        int temp = array[j];
                        array[j] = array[j - 1];
                        array[j - 1] = temp;
                    }
                }
            }
        }
    }

插入排序的原理：

主要的实现思想是将数据按照一定的顺序一个一个的插入到有序的表中，最终得到的序列就是已经排序好的数据。

例如采用插入排序算法将无序表{3,1,7,5,2,4,9,6}进行升序排序的过程为：

• 首先考虑记录 3 ，由于插入排序刚开始，有序表中没有任何记录，所以 3 可以直接添加到有序表中，则有序表和无序表可以如图 1 所示：

                                                               图 1 直接插入排序（1）

• 向有序表中插入记录 1 时，同有序表中记录 3 进行比较，1<3，所以插入到记录 3 的左侧，如图 2 所示：

                                                                图 2 直接插入排序（2）

• 向有序表插入记录 7 时，同有序表中记录 3 进行比较，3<7，所以插入到记录 3 的右侧，如图 3 所示：

                                                                图 3 直接插入排序（3）

• 向有序表中插入记录 5 时，同有序表中记录 7 进行比较，5<7，同时 5>3，所以插入到 3 和 7 中间，如图 4 所示：

                                                                图 4 直接插入排序（4）

• 向有序表插入记录 2 时，同有序表中记录 7进行比较，2<7，再同 5，3，1分别进行比较，最终确定 2 位于 1 和 3 中间，如图 5 所示：

                                                                图 5 直接插入排序（5）

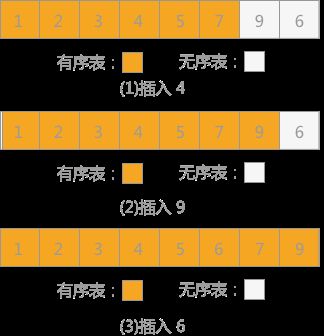
• 照此规律，依次将无序表中的记录 4，9 和 6插入到有序表中，如图 6 所示：

                                                       图 6 依次插入记录4，9和6

注意：

以第一个为有序数组，之后的所有元素依次插入到这个有序数组中，插入时，必须保证
数组一直有序！！！

插入排序的实现：

	public static void insertSort(int[] arr) {
		for (int i = 0; i < arr.length - 1; i++) {
			// 取下一个元素，倒着插入，保证插入时数组一直有序
			for (int j = i + 1; j > 0; j--) {
				if (arr[j] < arr[j - 1]) {
					arr[j] = arr[j] ^ arr[j - 1];   
		            arr[j -1] = arr[j] ^ arr[j - 1]; 
		            arr[j] = arr[j] ^ arr[j - 1]; 
				}
			}
		}
	}

选择排序的原理：

对于具有 n 个记录的无序表遍历 n-1 次，第 i 次从无序表中第 i 个记录开始，找出后序关键字中最小的记录，然后放置在第 i 的位置上。

例如对无序表{56，12，80，91，20}采用简单选择排序算法进行排序，具体过程为：

• 第一次遍历时，从下标为 1 的位置即 56 开始，找出关键字值最小的记录 12，同下标为 0 的关键字 56 交换位置：

• 第二次遍历时，从下标为 2 的位置即 56 开始，找出最小值 20，同下标为 2 的关键字 56 互换位置：

• 第三次遍历时，从下标为 3 的位置即 80 开始，找出最小值 56，同下标为 3 的关键字 80 互换位置：

• 第四次遍历时，从下标为 4 的位置即 91 开始，找出最小是 80，同下标为 4 的关键字 91 互换位置：

• 到此简单选择排序算法完成，无序表变为有序表。

选择排序的实现： 

public static void selectSort(int[] arr) {
		for (int i = 0; i < arr.length - 1; i++) {
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[j] < arr[i]) {
					arr[j] = arr[j] ^ arr[i];   
		            arr[i] = arr[j] ^ arr[i]; 
		            arr[j] = arr[j] ^ arr[i]; 
				}
			}
		}
	}

二分（折半）查找的原理：

折半查找，也称二分查找，在某些情况下相比于顺序查找，使用折半查找算法的效率更高。但是该算法的使用的前提是列表中的数据必须是有序的。

例如，在{5,21,13,19,37,75,56,64,88 ,80,92}这个列表使用折半查找算法查找数据之前，需要首先对该表中的数据按照所查的关键字进行排序：{5,13,19,21,37,56,64,75,80,88,92}。

 对列表{5,13,19,21,37,56,64,75,80,88,92}采用折半查找算法查找关键字为 21 的过程为：
 

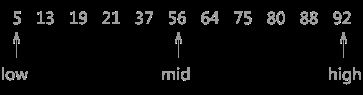
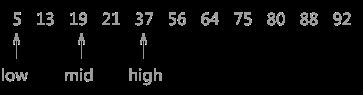
                                                                 图1 折半查找的过程（a）

如上图 1 所示，指针 low 和 high 分别指向列表的第一个关键字和最后一个关键字，指针 mid 指向处于 low 和 high 指针中间位置的关键字。在查找的过程中每次都同 mid 指向的关键字进行比较，由于整个表中的数据是有序的，因此在比较之后就可以知道要查找的关键字的大致位置。

例如在查找关键字 21 时，首先同 56 作比较，由于21 < 56，而且这个列表是按照升序进行排序的，所以可以判定如果列表中有 21 这个关键字，就一定存在于 low 和 mid 指向的区域中间。

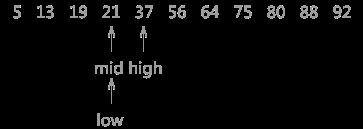
因此，再次遍历时需要更新 high 指针和 mid 指针的位置，令 high 指针移动到 mid 指针的左侧一个位置上，同时令 mid 重新指向 low 指针和 high 指针的中间位置。如图 2 所示：
 

                                                                图 2 折半查找的过程（b）

同样，用 21 同 mid 指针指向的 19 作比较，19 < 21，所以可以判定 21 如果存在，肯定处于 mid 和 high 指向的区域中。所以令 low 指向 mid 右侧一个位置上，同时更新 mid 的位置。
 

                                                                图 3 折半查找的过程（3）

当第三次做判断时，发现 mid 就是关键字 21 ，查找结束。

// 二分查找
	public static int binarySearch01(int[] arr, int key) {
		int low = 0, high = arr.length - 1;
		while (low <= high) {
			int middle = (low + high) >> 1;
			
			if (arr[middle] > key) {
				high = middle - 1;
			} else if (arr[middle] < key) {
				low = middle + 1;
			} else {
				return middle;
			}
		}
		return -1;
	}



// 二分查找，递归完成
public static int binarySearch02(int[] arr, int key, int low, int higt) {
		if (low > high) {
			return -1;
		}

		int middle = (low + high) >> 1;
		if (key == arr[middle]) {
			return middle;
		} else if (key > arr[middle]) {
			return binarySearch02(arr, key, middle + 1,high);
		} else {
			return binarySearch02(arr, key, low, middle - 1);
		} 
	}