什么是红黑树，以及如何实现红黑树的插入操作

目录

一.前言

二.红黑树的概述

三.红黑树的插入操作

四.红黑树的应用

五.代码实现

---

一.前言

我们知道按照二叉树排序的特点进行数据的插入，可能会产生以下这种情况：

这种情况下，会使二叉排序树的查找性能大打折扣，几乎变成了线性查找，所以为了解决二叉排序树多次插入新节点导致的不平衡问题，诞生了红黑树。

二.红黑树的概述

红黑树（ Red black tree）是一种自平衡二叉査找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。红黑树和AVL树类似，都是在进行插λ和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O（logn）时间内做查找，插入和删除，这里的n是树中元素的数目。

1.红黑树的操作

在红黑树上只读操作不需要对用于二叉査找树的操作做岀修改，因为它也是二叉査找树。但是，在插入和删除之后，红黑属性可能变得违规。恢复红黑属性需要少量的颜色变更（这在实践中是非常快速的）并且在删除节点是不超过三次树旋转（对于插入是不超过两次树旋转）。

红黑树（RBT）的定义：它或者是一颗空树，或者是具有一下性质的二叉查找树：

1. 节点非红即黑。
2. 根节点是黑色。
3. 所有NULL结点称为叶子节点，且认为颜色为黑。
4. 所有红节点的子节点都为黑色。
5. 从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

所有性质1~5合起来约束了该树的平衡性能--即该树上的最长路径不可能会大于2倍最短路径。因为，最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

三.红黑树的插入操作

由于性质的约束：插入点不能为黑节点，应插入红节点。因为你插入黑节点将破坏性质5，所以每次插入的点都是红结点，但是若他的父节点也为红，那岂不是破坏了性质4？对啊，所以要做一些“旋转”和一些节点的变色！另为叙述方便我们给要插入的节点标为N（红色），父节点为P，祖父节点为G，叔节点为U。下边将一一列出所有插入时遇到的情况：

情形1：该树为空树，直接插入根结点的位置，违反性质1，把节点颜色有红改为黑即可。

情形2：插入节点N的父节点P为黑色，不违反任何性质，无需做任何修改。

情形3：N为红，P为红，（祖节点一定存在，且为黑，下边同理）U也为红，这里不论P是G的左孩子，还是右孩子；不论N是P的左孩子，还是右孩子。

操作：如图把P、U改为黑色，G改为红色，未结束。

因为N、P都为红，违反性质4；若把P改为黑，符合性质4，显然左子树多了一个黑节点，违反性质5；所以我们把P，G，U都改为相反色，这样一来通过G的路径的黑节点数目没变，即符合4、5，但是G变红了，若G的父节点又是红的，不就有违反了4？所以经过上边操作后并未结束，需把G作为起始点，即把G看做一个新插入的红节点继续向上检索----属于哪种情况，按那种情况操作~要么中间就结束，要么直到根结点（上图这种情况下，G就是根结点，根结点变红，根结点向上检索，没有其他节点了，就把根结点G变为黑色）。

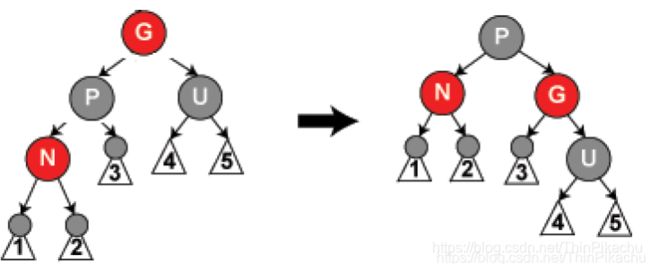
情形4：N为红，P为红，U为黑（或不存在），P为G的左孩子，N为P的左孩子（或者P为G的右孩子，N为P的右孩子；反正就是同向的）。

 

操作：如图P、G变色，接着以G为轴做右单旋转（或左单旋转），结束。

解析：要知道经过P、G变换（旋转），变换后P的位置就是原来G的位置，所以红P变为黑，而黑G变为红都是为了不违反性质5，而维持到达叶节点所包含的黑节点的数目不变。

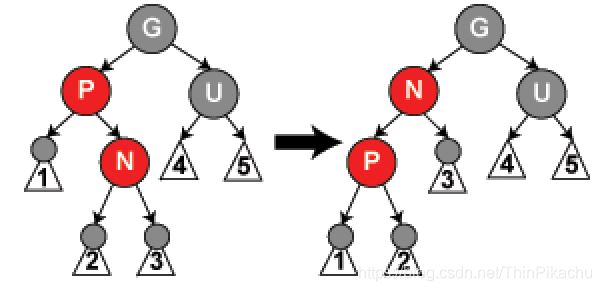
情形5：N为红，P为红，U为黑（或不存在），P为G的左孩子，N为P的右孩子（或者P为G的右孩子，N为P的左孩子；反正两方向相反）。

 

操作：需要进行两次变换（旋转），图中只显示了一次变换-----首先P、N变换，颜色不变，以P为轴做一次左单旋转（或右单旋转）；然后就变成了情形4的情况，按照情况4操作，即结束。

解析：由于P、N都为红，经变换，不违反性质5；然后就变成4的情形，此时G与G现在的左孩子变色，并变换，结束。

四.红黑树的应用

• linux进程调度 Completely Fair Scheduler用红黑树管理进程控制块。
• epoll在内核中的实现，用红黑树管理事件块。
• nginx中，用红黑树管理 timer等。
• STL中的map，set， mutil_map， mutil_set关联容器
• Java的 TreeMap实现 

五.代码实现

1.红黑树结构的定义

#include
#include
#include
#include // memset;
#include
#include
#include
#include
using namespace std;

typedef enum { RED = 0, BLACK = 1 } ColorType;//利用enum(枚举）定义节点的颜色
typedef int KeyType;//节点中存放的数据类型
typedef struct rb_node//节点的结构体实现
{
	struct rb_node* leftchild;
	struct rb_node* parent;
	struct rb_node* rightchild;
	ColorType color; 
	KeyType  key;
}rb_node;

typedef struct//红黑树的结构体实现
{
	struct rb_node* head;
    /*head的parent指向红黑树的根结点,而left和right分别指向这棵红黑树的最小值和最大值*/

	struct rb_node* Nil;//哨兵节点（叶子节点）
	int cursize;//cursize代表当前红黑树中节点的个数
}RBTree;

例如： 

2.红黑树的初始化

struct rb_node* Buynode(struct rb_node* pa, ColorType color)//申请红黑树节点
{
	struct  rb_node* s = (struct rb_node*)malloc(sizeof(struct rb_node));
	if (NULL == s) exit(EXIT_FAILURE);
	memset(s, 0, sizeof(struct rb_node));
	return s;
}
void Freenode(struct rb_node* p)//释放红黑树节点
{
	free(p);
}

/*空的红黑树只有头结点和哨兵节点*/
void Init_RBTree(RBTree* ptree)//初始化红黑树
{
	assert(ptree != NULL);
	ptree->cursize = 0;
	ptree->Nil = Buynode(NULL, BLACK);      // NIL 
	ptree->head = Buynode(ptree->Nil, RED); // HEAD
	ptree->head->leftchild = ptree->head->rightchild =ptree->head->parent= ptree->Nil;
}

 3.左单旋转的实现

void RotateLeft(RBTree* ptree, struct rb_node* ptr)/*左单旋转*//*ptree代表红黑树，ptr代表轴节点*/
{
	struct rb_node* newroot = ptr->rightchild;
	newroot->parent = ptr->parent; // 1
	ptr->rightchild = newroot->leftchild;
	if (newroot->leftchild != NULL)
	{
		newroot->leftchild->parent = ptr;//2
	}
	newroot->leftchild = ptr;
	if (ptr == ptree->head->parent) // 如果ptr为根结点
	{
		ptree->head->parent = newroot;
	}
	else
	{
		if (ptr == ptr->parent->leftchild)
		{
			ptr->parent->leftchild = newroot;
		}
		else
		{
			ptr->parent->rightchild = newroot;
		}
	}
	ptr->parent = newroot; // 3
}

例如在下图中，节点p就是ptr，而节点newroot为N

4.右单旋转

void RotateRight(RBTree* ptree, struct rb_node* ptr)/*右单旋转*//*ptree代表红黑树，ptr代表轴节点*/
{
	struct rb_node* newroot = ptr->leftchild;
	newroot->parent = ptr->parent; // 1
	ptr->leftchild = newroot->rightchild;
	if (newroot->rightchild != NULL)
	{
		newroot->rightchild->parent = ptr; //2
	}
	newroot->rightchild = ptr;
	if (ptr == ptree->head->parent)//如果
	{
		ptree->head->parent = newroot;
	}
	else
	{
		if (ptr == ptr->parent->rightchild)
		{
			ptr->parent->rightchild = newroot;
		}
		else
		{
			ptr->parent->leftchild = newroot;
		}
	}
	ptr->parent = newroot;// 3
}

例如在下图中，节点G就是ptr，而节点P就是newroot

5.红黑树的插入操作

bool Insert(RBTree* ptree, KeyType kx)//kx代表要插入的值
{
	struct rb_node* pa = ptree->head;       // head
	struct rb_node* p = ptree->head->parent; // root;
	while (p != ptree->Nil && p->key != kx)
	{
		pa = p;//pa为p的父节点
		p = kx < p->key ? p->leftchild : p->rightchild;
	}
	if (p != ptree->Nil && p->key == kx) return false;//如果此时p不为空，且p->key=kx，说明 此时红黑树中已存在值为kx的节点
	//否则说明红黑树中不存在值为kx的节点，且此时p为空，则我们要进行插入
	p = Buynode(pa, RED);
	p->key = kx;
	p->leftchild = p->rightchild = ptree->Nil;//先将p的左右孩子分别指向空
	p->parent = pa;
	if (pa == ptree->head)//这种情况即情况一，该树为空树，直接将p插入根结点的位置
	{
		ptree->head->parent = p;
		ptree->head->leftchild = p;
		ptree->head->rightchild = p;
		//p->color = BLACK;
	}
	else
	{
		if (p->key < pa->key)//如果p的值小于pa的值，则先将它插入到pa的左边，我们后续在进行调整
		{
			pa->leftchild = p;
			if (p->key < ptree->head->leftchild->key)
			{
				ptree->head->leftchild = p;
			}
		}
		else//如果p的值大于pa的值，则先将它插入到pa的右边，我们后续在进行调整
		{
			pa->rightchild = p;
			if (p->key > ptree->head->rightchild->key)
			{
				ptree->head->rightchild = p;
			}
		}
	}
	ptree->cursize += 1;//红黑树总节点的个数+1
	Adjust_Tree(ptree, p);//此时再对红黑树进行调整
	return true;
}

void Adjust_Tree(RBTree* ptree, struct rb_node* ptr)//注意，此时的ptr就是我们新插入的节点
{
	struct rb_node* _X = ptr, * _Y = NULL;
	for (; _X != ptree->head->parent && _X->parent->color == RED;)
	{
		if (_X->parent == _X->parent->parent->rightchild) //此时X插入到了某一个节点的右边
		{
			_Y = _X->parent->parent->leftchild;//_Y为_X的叔叔节点
			if (_Y->color == RED)//此时_X，_X的父节点以及_X的叔叔节点的颜色全部为红色, 即情况3
			{
				//则将他们三个的颜色互换
				_Y->color = BLACK;
				_X->parent->color = BLACK;
				_X->parent->parent->color = RED;
				_X = _X->parent->parent;/*需把_X的爷爷节点作为起始点，即把_X的爷爷节点看做一个新插入的红节点继续向上检索----属于哪种情况，按那种情况操作~要么中间就结束，要么直到根结点*/
			}
			else//_Y即_X的叔叔节点的颜色为黑色，且此时_X，_X的父节点的颜色为红色
			{
				if (_X == _X->parent->leftchild)
				{
					/*此时_X是他父节点的左孩子，而_X的父节点是他的父节点的右节点，二者方向相反，情况5*/
					_X = _X->parent;
					RotateRight(ptree, _X);//做右单旋转，此后变为情况四
				}
				//下面为情况四
				_X->parent->color = BLACK;
				_X->parent->parent->color = RED;
				RotateLeft(ptree, _X->parent->parent);//再做一次左单旋转，
			}
		}
		else // //此时X插入到了某一个节点的左边，解决方法与上面相同
		{
			_Y = _X->parent->parent->rightchild;
			if (_Y->color == RED)
			{
				_Y->color = BLACK;
				_X->parent->color = BLACK;
				_X->parent->parent->color = RED;
				_X = _X->parent->parent;
			}
			else
			{
				if (_X == _X->parent->rightchild)
				{
					_X = _X->parent;
					RotateLeft(ptree, _X);
				}
				_X->parent->color = BLACK;
				_X->parent->parent->color = RED;
				RotateRight(ptree, _X->parent->parent);
			}
		}
	}
	ptree->head->parent->color = BLACK;//将根结点的颜色设为黑色
}

6.红黑树的查找操作【非递归】

struct rb_node* FindValue(RBTree* ptree, KeyType kx)
{
	if (ptree == NULL) return NULL;
	struct rb_node* p = ptree->head->parent; // root;
	while (p != ptree->Nil && p->key != kx)
	{
		p = kx < p->key ? p->leftchild : p->rightchild;
	}
	if (p == ptree->Nil)
	{
		p = NULL;
	}
	return p;
}

7.红黑树的查找操作【递归】

struct rb_node* SearchValue(RBTree* ptree, KeyType kx)
{
	struct rb_node* p = NULL;
	if (ptree != NULL)
	{
		p = Search(ptree, ptree->head->parent, kx);
	}
	return p;
}

struct rb_node* Search(RBTree* ptree, struct rb_node* ptr, KeyType kx)
{
	if (ptr == ptree->Nil) return NULL;
	else if (ptr->key == kx) return ptr;
	else if (kx < ptr->key)
		return Search(ptree, ptr->leftchild, kx);
	else
		return Search(ptree, ptr->rightchild, kx);
}

8.红黑树的非递归中序遍历

void NiceInOrder(RBTree* ptree)//非递归中序遍历
{
	assert(ptree != NULL);
	for (struct rb_node* p = First(ptree, ptree->head->parent); p != NULL; p = Next(ptree, p))
	{
		cout << p->key << "  ";
	}
	cout << endl;
}

struct rb_node* First(RBTree* ptree, struct rb_node* ptr)
{
	while (ptr != ptree->Nil && ptr->leftchild != ptree->Nil)
	{
		ptr = ptr->leftchild;
	}
	return ptr;
}
struct rb_node* Next(RBTree* ptree, struct rb_node* ptr)
{
	if (ptr == NULL || ptr == ptree->Nil) return NULL;
	if (ptr->rightchild != ptree->Nil)
	{
		return First(ptree, ptr->rightchild);
	}
	else
	{
		struct rb_node* pa = ptr->parent;
		while (pa != ptree->head && ptr != pa->leftchild)
		{
			ptr = pa;
			pa = ptr->parent;
		}
		if (pa == ptree->head)
		{
			pa = NULL;
		}
		return pa;
	}
}

9.红黑树的非递归逆中序遍历

void ResNiceInOrder(RBTree* ptree)
{
	assert(ptree != NULL);
	for (struct rb_node* p = Last(ptree, ptree->head->parent); p != NULL; p = Prev(ptree, p))
	{
		cout << p->key << "  ";
	}
	cout << endl;
}

struct rb_node* Last(RBTree* ptree, struct rb_node* ptr)
{
	while (ptr != ptree->Nil && ptr->rightchild != ptree->Nil)
	{
		ptr = ptr->rightchild;
	}
	return ptr;
}

struct rb_node* Prev(RBTree* ptree, struct rb_node* ptr)
{
	if (ptr == NULL || ptr == ptree->Nil) return NULL;
	if (ptr->leftchild != ptree->Nil)
	{
		return Last(ptree, ptr->leftchild);
	}
	else
	{
		struct rb_node* pa = ptr->parent;
		while (pa != ptree->head && ptr != pa->rightchild)
		{
			ptr = pa;
			pa = ptr->parent;
		}
		if (pa == ptree->head)
		{
			pa = NULL;
		}
		return pa;
	}
}