红黑树理论详解与Java实现

基本定义

红黑树是一颗二叉搜索树，它在每个结点上增加了一个存储位来表示结点的颜色，可以是红色或者黑色。
通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出2倍，因而是近似平衡的。

五大性质

1、结点必须是红色或者黑色。
2、根节点是黑色。
3、叶子结点（外部结点、空结点，不是传统上认为的那种叶子结点，如图中的那些NIL结点）都是黑色
4、红色结点的子结点都是黑色
于是有推论：
  4.1、红色结点的父结点都是黑色
  4.2、从根结点到叶子结点的所有路径上不能有两个连续的红色结点
5、从任一结点到叶子结点（外部结点、空结点，不是传统上认为的那种叶子结点，如图中的那些NIL结点）的所有路径都包含相同数目的黑色结点
如图所示：

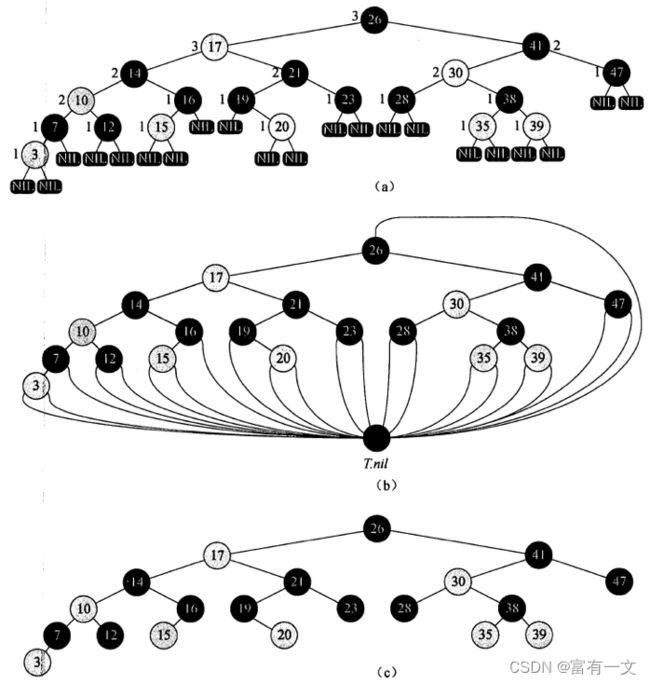
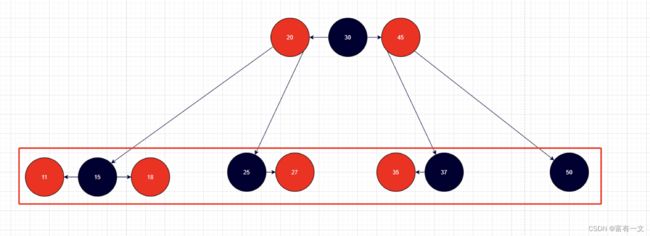
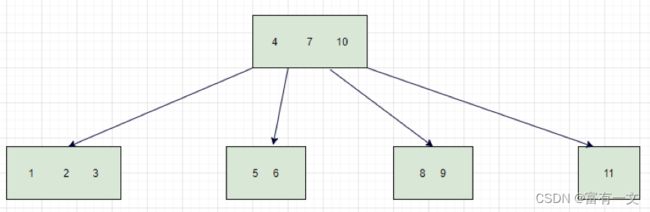
红黑树和2-3-4树的关系

红黑树和4阶B树（2-3-4树）具有等价性
黑色节点与它的红色子节点融合在一起，形成一个B树节点
红黑树的黑色节点个数与4阶B树的节点总个数相等

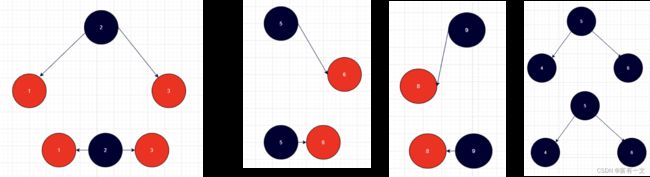
红黑树和2-3-4树各结点对应关系

红黑红、黑红、红黑、黑

添加结点到红黑树

注意事项

一般新添加的节点默认为红色，这样对红黑树的性质影响最小（性质1、2、3、5都满足，性质4不一定）
如果新添加的节点是根节点，染成黑色即可

添加的所有情况

添加结点到红黑树总共有12中情况；

有4种情况满足红黑树的性质，父节点为黑色节点，因此不需要做任何处理。如下图所示的4种紫红色节点添加情况

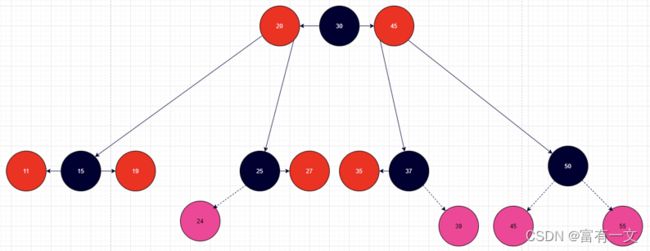
有8种情况不满足红黑树的性质，父节点为红色节点（但其实可以归纳为3种情况）。如下图所示的8种紫红色节点添加情况。

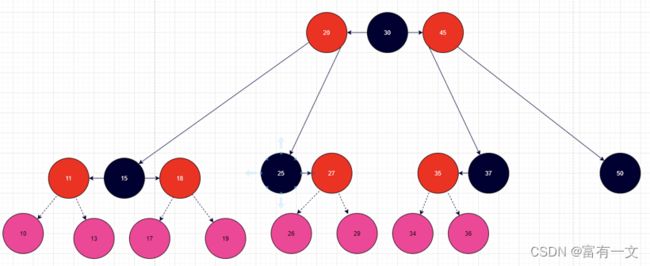
添加导致不平衡

添加结点导致红黑树出现不平衡的情况。

叔父节点不是红色节点（祖父节点为红色）

添加不平衡LL/RR

判断条件：叔父节点不是红色节点
父节点是祖父节点的左孩子，自己是父节点的左孩子（LL)
父节点是祖父节点的右孩子，自己是父节点的右孩子（RR)
如何恢复平衡：
1、父节点染成黑色，祖父节点染成红色
2、对祖父节点进行旋转操作（LL是右旋，RR是左旋）

添加不平衡LR/RL

判断条件：叔父节点不是红色节点
父节点是祖父节点的左孩子，自己是父节点的右孩子（LR)
父节点是祖父节点的右孩子，自己是父节点的左孩子（RL)
如何恢复平衡：
1、把自己染成黑色，祖父节点染成红色
2、进行两次旋转，第一次旋转是转换成LL/RR情况，第二次旋转恢复平衡
2.1、LR：先按照父节点左旋，变成LL，再按照祖父节点右旋
2.2、RL：先按照父节点右旋，变成RR，再按照祖父节点左旋

叔父节点是红色节点（祖父节点为黑色）

判断条件：叔父节点为红色
如何恢复平衡：
1、父节点、叔父节点都染成黑色
2、祖父节点染成红色，并把祖父节点当成新添加的节点，继续处理
2.1、如果祖父节点染成红色没有引起双红现象，则处理结束
2.2、如果祖父节点染成红色也导致双红现象，则继续按照是LL/RR，LR/RL，还是叔父节点为红色的三种情况处理，最差情况是处理直到根节点，把根节点染成了红色，这个时候只需要把根节点染成黑色即可。

删除

B树中，最后真正被删除的元素都在叶子节点中。详细见B树（B-tree、B-树）理论详解

删除节点就是上面图的4种情况。

删除红色节点

直接删除，无需任何调整

删除黑色节点

有3种情况
1、拥有两个红色子节点的黑色节点不可能直接被删除，因为会找它的红色子节点替代删除，因此这种情况无需考虑
2、拥有1个红色子节点的黑色节点 (删除黑色节点后，把替代的红色子节点染成黑色即可)
3、黑色叶子节点 (情况比较复杂)

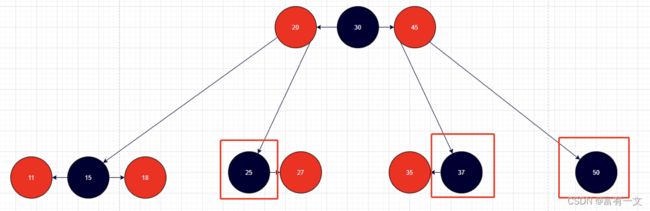
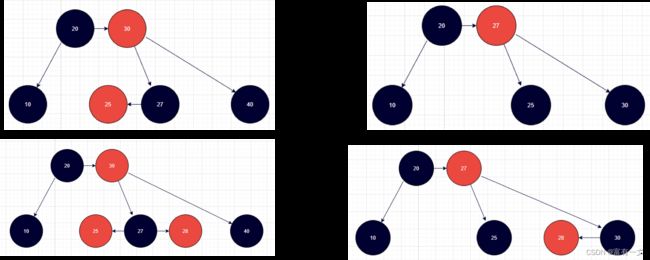
删除黑色叶子节点——情况一

如果兄弟节点是红色节点,
1、把兄弟节点染成黑色，父节点染成红色，对父节点进行旋转2、此时兄弟节点变成黑色，可以继续按照情况2，3，4进行处理

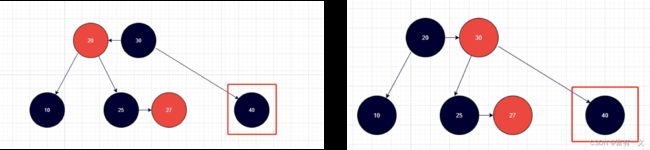
如图所示，40结点的兄弟结点是20，父结点是30。

删除黑色叶子节点——情况二

黑色兄弟节点没有一个红色子节点，
1、如果父节点是红色，把兄弟节点染成红色，父节点染成黑色，完成平衡维护。
2、如果父节点是黑色，把兄弟节点染成红色，把父节点当成待删除的节点，向上递归或循环处理（依然有情况1，2，3，4）。

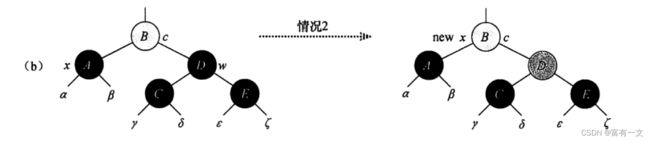
删除黑色叶子节点——情况三

兄弟节点是左节点，黑色兄弟节点的左孩子是黑色节点，为LR场景，需要先转变为LL，方便后面的平衡旋转。
1、把兄弟节点的右孩子设为黑色，兄弟节点设为红色，对兄弟节点进行左旋，确保兄弟节点有一个红色左孩子，此时变成情况4。

删除黑色叶子节点——情况四

兄弟节点是左节点，兄弟节点的左孩子是红色节点，LL场景，
1、把兄弟节点的颜色设置为父节点的颜色，父节点和兄弟节点的左孩子都设置为黑色，
对父节点进行右旋，恢复平衡。

红黑树与AVL（平衡二叉树）树比较

AVL树的平衡标准比较严格：每个左右子树的高度差不超过1。
红黑树的平衡标准比较宽松：没有一条路径会大于其他路径的两倍。
相对于AVL树来说，红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作，总体性能要优于 AVL树。
红黑树的平均统计性能优于AVL树，实际应用中更多选择使用红黑树。

红黑树与B树B+树比较

红黑树的分叉少，适合在内存中使用，如果在硬盘中使用的话，当数据量大的时候，红黑树的层高比较高，会带来比较多的磁盘IO，影响查询性能，比如说100万的数据量，用红黑树的话，大概是20层的层高，会有20次磁盘IO。
B树和B+树的分叉比较多，B树分叉一般能到两三百，B+树分叉多的能到上千，所以B树和B+树适合磁盘存储，100万的数据量，一般3层树高即可搞定，只有3次磁盘IO，实际中数据库一般把根节点存放在内存中，所以其实只有两次IO。

完整的Java测试代码

RedBlackTree

package redblacktree;

public class RedBlackTree implements BinaryTreeInfo {
    //红黑直接用布尔变量定义
    private static final boolean RED = false;
    private static final boolean BLACK = true;

    //初始化一个唯一的叶结点
    private final RBNode nil = new RBNode();

    //根结点初始化为nil
    private RBNode root = nil;

    public RBNode getRoot() {
        return root;
    }

    public void setRoot(RBNode root) {
        this.root = root;
    }

    public RedBlackTree() {
        this.root = nil;
    }

    public RedBlackTree(RBNode root) {
        this.root = root;
    }

    //前序遍历二叉树
    public void preorderTreeWalk(RBNode x) {
        if(x != nil) {
            System.out.print(x.key + " ");
            preorderTreeWalk(x.left);
            preorderTreeWalk(x.right);
        }
    }

    //中序遍历二叉树
    public void inorderTreeWalk(RBNode x) {
        if(x != nil) {
            inorderTreeWalk(x.left);
            System.out.print(x.key + " ");
            inorderTreeWalk(x.right);
        }
    }

    //后序遍历二叉树
    public void postorderTreeWalk(RBNode x) {
        if(x != nil) {
            postorderTreeWalk(x.left);
            postorderTreeWalk(x.right);
            System.out.print(x.key + " ");
        }
    }

    //在二叉搜索树中查询某个值，递归版本
    public RBNode treeSearch(RBNode x, Integer k) {
        if(x == nil || k == x.key) {
            return x;
        }

        if(k < x.key) {
            return treeSearch(x.left, k);
        } else {
            return treeSearch(x.right, k);
        }
    }

    //在二叉搜索树中查询某个值，循环版本
    public RBNode iterativeTreeSearch(RBNode x, Integer k) {
        while(x != nil && k != x.key) {
            if(k < x.key) {
                x = x.left;
            } else {
                x = x.right;
            }
        }

        return x;
    }

    //在二叉搜索树中查找包含最小值的节点
    public RBNode treeMinimum(RBNode x) {
        while (x.left != nil) {
            x = x.left;
        }

        return x;
    }

    //在二叉搜索树中查找包含最大值的节点
    public RBNode treeMaximum(RBNode x) {
        while (x.right != nil) {
            x = x.right;
        }

        return x;
    }

    //查找节点x的后继节点
    public RBNode treeSuccessor(RBNode x) {
        if(x.right != nil) {  //x的右子树不为空，找右子树的最小值
            return treeMinimum(x.right);
        }

        RBNode y = x.parent;
        while(y != nil && x == y.right) {
            x = y;
            y = y.parent;
        }

        return y;
    }

    //查找节点x的前驱节点
    public RBNode treePredeceessor(RBNode x) {
        if(x.left != nil) {
            return treeMaximum(x.left);
        }

        RBNode y = x.parent;
        while(y != nil && x == y.left) {
            x = y;
            y = y.parent;
        }

        return y;
    }

    /**
     * 围绕x左旋
     *       xp                    xp
     *      /                     /
     *     x                     xr
     *    / \          ==>      / \
     *  xl  xr                 x   rr
     *     / \                / \
     *    rl  rr             xl  rl
     *
     * @param t,x
     */
    void leftRotate(RedBlackTree t, RBNode x) {
        RBNode y = x.right;   //让y等于x的右子节点
        x.right = y.left;    //将y的左子树转成x的右子树
        if(y.left != t.nil) {  //假如y的左孩子不为空，将y的左孩子的父亲设置为x
            y.left.parent = x;
        }
        y.parent = x.parent;  //将y的父亲设置为x的父亲
        if(x.parent == t.nil) {
            t.root = y;  //考虑x原来为根节点的情况
        } else if (x.parent.left == x) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }

        y.left = x;
        x.parent = y;
    }

    /**
     * 围绕x右旋
     *    xp                xp
     *     \                 \
     *      x                xl
     *     / \      =>      /  \
     *   xl  xr            ll   x
     *   / \                   / \
     *  ll lr                 lr  xr
     *
     * @param t,x
     */
    void rightRotate(RedBlackTree t, RBNode x) {
        RBNode y = x.left;   //让y等于x的左子节点
        x.left = y.right;    //将y的右子树转成x的左子树
        if(y.right != t.nil) {  //假如y的右孩子不为空，将y的右孩子的父亲设置为x
            y.right.parent = x;
        }
        y.parent = x.parent;  //将y的父亲设置为x的父亲
        if(x.parent == t.nil) {
            t.root = y;  //考虑x原来为根节点的情况
        } else if (x.parent.left == x) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }

        y.right = x;
        x.parent = y;
    }


    //红黑树的插入操作
    public void RBInsert(RedBlackTree t, RBNode z) {
        RBNode y = t.nil;
        RBNode x = t.root;
        while(x != t.nil) {
            y = x;
            if(z.key < x.key) {
                x = x.left;
            } else {
                x = x.right;
            }
        }

        z.parent = y;
        if(y == t.nil) {  //说明现在是棵空树
            t.root = z;
        } else if (z.key < y.key) {
            y.left = z;
        } else {
            y.right = z;
        }

        z.left = t.nil;
        z.right = t.nil;
        z.color = RED;
        rbInsertFixup(t, z);
    }

    //插入节点后维护红黑树性质的过程
    public void rbInsertFixup(RedBlackTree t, RBNode z) {
        while (z.parent.color == RED) {
            if(z.parent == z.parent.parent.left) {  //z的父节点是z的祖父节点的左孩子
                RBNode y = z.parent.parent.right;   //让y成为z的叔叔节点
                if (y.color == RED) {
                    /*
                     * z的父亲和叔叔节点都是红色，
                     * 根据红黑树性质，z的祖父一定是黑色
                     * 所以这时候，可以把z的祖父设为红色，
                     * z的父亲和叔叔都设为黑色，但这可能
                     * 导致z的祖父产生双红节点的问题，这
                     * 时候把z设置成z的祖父，继续向上递归
                     */
                    z.parent.color = BLACK;
                    y.color = BLACK;
                    z.parent.parent.color = RED;
                    z = z.parent.parent;
                } else {
                    if (z == z.parent.right) {
                        /*
                         * z的父亲是左节点，z是右节点,
                         * 满足LR不平衡，需要对z的父亲进行左旋,
                         * 转变成LL不平衡
                         */
                        z = z.parent;
                        leftRotate(t, z);
                    }
                    /*
                     * z的父亲是左节点，z也是左节点，
                     * 满足LL不平衡，把z的父亲设为黑色，
                     * z的祖父设为红色，对z进行右旋，
                     * 即可满足平衡
                     */
                    z.parent.color = BLACK;
                    z.parent.parent.color = RED;
                    rightRotate(t, z.parent.parent);
                }
            } else {
                RBNode y = z.parent.parent.left;   //让y成为z的叔叔节点
                if (y.color == RED) {
                    /*
                     * z的父亲和叔叔节点都是红色，
                     * 根据红黑树性质，z的祖父一定是黑色
                     * 所以这时候，可以把z的祖父设为红色，
                     * z的父亲和叔叔都设为黑色，但这可能
                     * 导致z的祖父产生双红节点的问题，这
                     * 时候把z设置成z的祖父，继续向上递归
                     */
                    z.parent.color = BLACK;
                    y.color = BLACK;
                    z.parent.parent.color = RED;
                    z = z.parent.parent;
                } else {
                    if (z == z.parent.left) {
                        /*
                         * z的父亲是右节点，z是左节点,
                         * 满足RL不平衡，需要对z的父亲进行右旋,
                         * 转变成RR不平衡
                         */
                        z = z.parent;
                        rightRotate(t, z);
                    }
                    /*
                     * z的父亲是右节点，z也是右节点，
                     * 满足RR不平衡，把z的父亲设为黑色，
                     * z的祖父设为红色，对z进行左旋，
                     * 即可满足平衡
                     */
                    z.parent.color = BLACK;
                    z.parent.parent.color = RED;
                    leftRotate(t, z.parent.parent);
                }
            }
        }

        t.root.color = BLACK;
    }

    public void rbTransplant(RedBlackTree t, RBNode u, RBNode v) {
        if(u.parent == t.nil) {
            t.root = v;
        } else if(u == u.parent.left) {
            u.parent.left = v;
        } else {
            u.parent.right = v;
        }

        v.parent = u.parent;
    }

    //删除节点操作
    public void rbDelete(RedBlackTree t, RBNode z) {
        RBNode x;
        RBNode y = z;
        boolean yOriginalColor = y.color;
        if (z.left == t.nil) {
            x = z.right;
            //z的左孩子为空，用z的右孩子替换z，此时z的右孩子可以为空，也可以不为空
            rbTransplant(t, z, z.right);
        } else if (z.right == t.nil) {
            x = z.left;
            //z仅有一个孩子且其为左孩子，用z的左孩子替换z
            rbTransplant(t, z , z.left);
        } else {
            //z有两个孩子，找z的后继节点
            y = treeMinimum(z.right);

            yOriginalColor = y.color;
            x = y.right;
            if(y.parent == z) {
                x.parent = y;
            } else {
                //用以y的右孩子为根的树代替以y为根的树
                rbTransplant(t, y, y.right);
                y.right = z.right;
                y.right.parent = y;
            }

            //用以y为根的树代替以z为根的树
            rbTransplant(t, z, y);
            y.left = z.left;
            y.left.parent = y;
        }

        //如果删除的为黑节点，需要修复平衡
        if (yOriginalColor == BLACK) {
//            rbDeleteFixup(t, x);
            fixAfterDelete(t, x);
        }
    }

    //删除修复算法导论版代码，用红黑树解释
    public void rbDeleteFixup(RedBlackTree t, RBNode x) {
        while(x != t.root && x.color == BLACK) {
            //x是左孩子
            if(x == x.parent.left) {
                //w为兄弟节点
                RBNode w = x.parent.right;
                //w为红色，要旋转成黑色，方便后续操作
                if(w.color == RED) {
                    w.color = BLACK;
                    x.parent.color = RED;
                    leftRotate(t, x.parent);
                    //此时w为黑色
                    w = x.parent.right;
                }

                /*
                 * w是黑色，w的两个孩子都是黑色，
                 * 没办法通过旋转恢复平衡，只能把w拉下水，设为红色，
                 * x变成x的父节点，向上递归
                 */
                if(w.left.color == BLACK && w.right.color == BLACK) {
                    w.color = RED;
                    x = x.parent;
                } else {
                    /*
                     * w是黑色，w的右孩子是黑色，
                     * w的左孩子是红色，为RL场景
                     * 此时把w的左孩子设为黑色，
                     * w设为红色，对w进行右旋，
                     * 确保w的右孩子为红色，此时为RR场景
                     */
                    if(w.right.color == BLACK) {
                        w.left.color = BLACK;
                        w.color = RED;
                        rightRotate(t, w);
                        w = x.parent.right;
                    }

                    /*
                     * 此时一定是w为黑色，w的右孩子为红色，
                     * w设置为x父节点的颜色，
                     * x父节点设为黑色，
                     * w的右孩子设置为黑色，
                     * 这样w路径上多出来一个黑节点，
                     * 对x的父节点进行左旋，
                     * 相当于把原来w路径上多出来的黑节点补充到x的路径上，
                     * 这样就填补了原来删除的黑节点，恢复平衡
                     */
                    w.color = x.parent.color;
                    x.parent.color = BLACK;
                    w.right.color = BLACK;
                    leftRotate(t, x.parent);
                    /*
                     * 这里已经恢复平衡，
                     * 所以直接把x设置为根节点结束循环
                     */
                    x = t.root;
                }
            } else {
                //x是右孩子，w是兄弟节点
                RBNode w = x.parent.left;
                //w为红色，要旋转成黑色，方便后续操作
                if(w.color == RED) {
                    w.color = BLACK;
                    x.parent.color = RED;
                    rightRotate(t, x.parent);
                    //此时w为黑色
                    w = x.parent.right;
                }

                /*
                 * w是黑色，w的两个孩子都是黑色，
                 * 没办法通过旋转恢复平衡，只能把w拉下水，设为红色，
                 * x变成x的父节点，向上递归
                 */
                if(w.right.color == BLACK && w.left.color == BLACK) {
                    w.color = RED;
                    x = x.parent;
                } else {
                    /*
                     * w是黑色，w的左孩子是黑色，
                     * w的右孩子是红色，为LR场景
                     * 此时把w的右孩子设为黑色，
                     * w设为红色，对w进行左旋，
                     * 确保w的左孩子一定为红色，此时为LL场景
                     */
                    if(w.left.color == BLACK) {
                        w.right.color = BLACK;
                        w.color = RED;
                        leftRotate(t, w);
                        w = x.parent.left;
                    }

                    /*
                     * 此时一定是w为黑色，w的左孩子为红色，
                     * w设置为x父节点的颜色，
                     * x父节点设为黑色，
                     * w的左孩子设置为黑色，
                     * 这样w路径上多出来一个黑节点，
                     * 对x的父节点进行右旋，
                     * 相当于把原来w路径上多出来的黑节点补充到x的路径上，
                     * 这样就填补了原来删除的黑节点，恢复平衡
                     */
                    w.color = x.parent.color;
                    x.parent.color = BLACK;
                    w.left.color = BLACK;
                    rightRotate(t, x.parent);
                    /*
                     * 这里已经恢复平衡，
                     * 所以直接把x设置为根节点结束循环
                     */
                    x = t.root;
                }
            }
        }
        /*
         * 循环结束，要么x是根节点，
         * 要么x是红色节点，
         * 直接把x设置成黑色，即可恢复平衡
         */
        x.color = BLACK;
    }

    /**
     * 根据2-3-4树解释的红黑树删除
     * 删除后的调整处理
     * 1.情况1：自己能搞定，对应的叶子节点是3节点或者4节点
     * 2.情况2：自己搞不定，需要兄弟节点借，但是兄弟节点不能直接借，找父亲节点借，父亲下来，然后兄弟节点找一个人代替父亲当家
     * 3.情况3：跟兄弟节点借，兄弟也没有
     * @param t,x
     */
    public void fixAfterDelete(RedBlackTree t, RBNode x){
        while(x != t.root && x.color == BLACK){
            //x是左孩子的情况
            if(x == x.parent.left) {
                //兄弟节点
                RBNode w = x.parent.right;

                //判断此时兄弟节点是否是真正的兄弟节点，只有黑色节点才是
                if(w.color == RED){
                    w.color = BLACK;
                    x.parent.color = RED;
                    leftRotate(t, x.parent);
                    //找到真正的兄弟节点
                    w = x.parent.right;
                }
                //情况三，找兄弟借，兄弟没得借
                if(w.left.color == BLACK && w.right.color == BLACK) {
                    //把兄弟拉下水，设为红色，向上递归
                    w.color = RED;
                    x = x.parent;
                }
                //情况二，找兄弟借，兄弟有的借
                else{
                    //确保w的右孩子是红色
                    if(w.right.color == BLACK) {
                        w.left.color = BLACK;
                        w.color = RED;
                        rightRotate(t, w);
                        w = x.parent.right;
                    }

                    /*
                     * 此时一定是w为黑色，w的右孩子为红色，
                     * w设置为x父节点的颜色，
                     * x父节点设为黑色，
                     * w的右孩子设置为黑色，
                     * 这样w路径上多出来一个黑节点，
                     * 对x的父节点进行左旋，
                     * 相当于把原来w路径上多出来的黑节点补充到x的路径上，
                     * 这样就填补了原来删除的黑节点，恢复平衡
                     */
                    w.color = x.parent.color;
                    x.parent.color = BLACK;
                    w.right.color = BLACK;
                    leftRotate(t, x.parent);

                    x = t.root;
                }
            }
            //x是右孩子的情况
            else{
                //兄弟节点
                RBNode w = x.parent.left;
                //判断此时兄弟节点是否是真正的兄弟节点，只有黑色节点才是
                if(w.color == RED) {
                    w.color = BLACK;
                    x.parent.color = RED;
                    rightRotate(t, x.parent);
                    //此时w为黑色，才是真正的兄弟节点
                    w = x.parent.right;
                }
                //情况三，找兄弟借，兄弟没得借
                if(w.left.color == BLACK && w.right.color == BLACK) {
                    //把兄弟拉下水，设为红色，向上递归
                    w.color = RED;
                    x = x.parent;
                }
                //情况二，找兄弟借，兄弟有的借
                else{
                    //确保w的左孩子是红色
                    if(w.left.color == BLACK) {
                        w.right.color = BLACK;
                        w.color = RED;
                        leftRotate(t, w);
                        w = x.parent.right;
                    }

                    /*
                     * 此时一定是w为黑色，w的左孩子为红色，
                     * w设置为x父节点的颜色，
                     * x父节点设为黑色，
                     * w的左孩子设置为黑色，
                     * 这样w路径上多出来一个黑节点，
                     * 对x的父节点进行右旋，
                     * 相当于把原来w路径上多出来的黑节点补充到x的路径上，
                     * 这样就填补了原来删除的黑节点，恢复平衡
                     */
                    w.color = x.parent.color;
                    x.parent.color = BLACK;
                    w.left.color = BLACK;
                    rightRotate(t, x.parent);

                    x = t.root;
                }
            }
        }
        //情况一、替代节点是红色，则直接染红，补偿删除的黑色节点，这样红黑树依然保持平衡
        x.color = BLACK;
    }

    //红黑树节点类定义
    static class RBNode {
        private Integer key;  //节点值
        private RBNode parent;  //父节点
        private RBNode left;   //左孩子
        private RBNode right;   //右孩子
        private boolean color = BLACK;

        public RBNode() {

        }

        public RBNode(Integer key) {
            this.key = key;
        }

        public RBNode(Integer key, RBNode parent) {
            this.parent = parent;
            this.color = BLACK;
            this.key = key;
        }

        public RBNode(RBNode parent, RBNode left, RBNode right, Integer key, boolean color) {
            this.parent = parent;
            this.left = left;
            this.right = right;
            this.key = key;
            this.color = color;
        }

        public Integer getKey() {
            return key;
        }

        public void setKey(Integer key) {
            this.key = key;
        }

        public RBNode getParent() {
            return parent;
        }

        public void setParent(RBNode parent) {
            this.parent = parent;
        }

        public RBNode getLeft() {
            return left;
        }

        public void setLeft(RBNode left) {
            this.left = left;
        }

        public RBNode getRight() {
            return right;
        }

        public void setRight(RBNode right) {
            this.right = right;
        }
    }

    @Override
    public Object root() {
        return root;
    }

    @Override
    public Object left(Object RBNode) {
        return ((RBNode)RBNode).left;
    }

    @Override
    public Object right(Object RBNode) {
        return ((RBNode)RBNode).right;
    }

    @Override
    public Object string(Object RBNode) {
        RBNode myRBNode = (RBNode)RBNode;

        String color = myRBNode.color == RED ? "RED" : "BLACK";

        return myRBNode.key + "(" + color + ")";
    }

    public static void main(String[] args) {
        RedBlackTree bst = new RedBlackTree();

        bst.RBInsert(bst, new RBNode(12));
        bst.RBInsert(bst, new RBNode(5));
        bst.RBInsert(bst, new RBNode(2));
        bst.RBInsert(bst, new RBNode(9));
        bst.RBInsert(bst, new RBNode(18));
        bst.RBInsert(bst, new RBNode(15));
        bst.RBInsert(bst, new RBNode(19));
        bst.RBInsert(bst, new RBNode(17));

        bst.inorderTreeWalk(bst.root);

        System.out.println();

        BinaryTrees.print(bst);

        bst.rbDelete(bst, bst.treeSearch(bst.root, 12));

        System.out.println();

        BinaryTrees.print(bst);
    }
}

BinaryTreeInfo

package redblacktree;

public interface BinaryTreeInfo {
	/**
	 * who is the root node
	 */
	Object root();
	/**
	 * how to get the left child of the node
	 */
	Object left(Object node);
	/**
	 * how to get the right child of the node
	 */
	Object right(Object node);
	/**
	 * how to print the node
	 */
	Object string(Object node);
}

BinaryTrees

package redblacktree;


public final class BinaryTrees {

	private BinaryTrees() {
	}

	public static void print(BinaryTreeInfo tree) {
		print(tree, null);
	}

	public static void println(BinaryTreeInfo tree) {
		println(tree, null);
	}

	public static void print(BinaryTreeInfo tree, PrintStyle style) {
		if (tree == null || tree.root() == null) return;
		printer(tree, style).print();
	}

	public static void println(BinaryTreeInfo tree, PrintStyle style) {
		if (tree == null || tree.root() == null) return;
		printer(tree, style).println();
	}

	public static String printString(BinaryTreeInfo tree) {
		return printString(tree, null);
	}

	public static String printString(BinaryTreeInfo tree, PrintStyle style) {
		if (tree == null || tree.root() == null) return null;
		return printer(tree, style).printString();
	}

	private static Printer printer(BinaryTreeInfo tree, PrintStyle style) {
		if (style == PrintStyle.INORDER) return new InorderPrinter(tree);
		return new LevelOrderPrinter(tree);
	}

	public enum PrintStyle {
		LEVEL_ORDER, INORDER
	}
}

InorderPrinter

package redblacktree;

/**

             ┌──800
         ┌──760
         │   └──600
     ┌──540
     │   └──476
     │       └──445
 ┌──410
 │   └──394
381
 │     ┌──190
 │     │   └──146
 │  ┌──40
 │  │  └──35
 └──12
    └──9
 */
public class InorderPrinter extends Printer {
	private static String rightAppend;
	private static String leftAppend;
	private static String blankAppend;
	private static String lineAppend;
	static {
		int length = 2;
		rightAppend = "┌" + Strings.repeat("─", length);
		leftAppend = "└" + Strings.repeat("─", length);
		blankAppend = Strings.blank(length + 1);
		lineAppend = "│" + Strings.blank(length);
	}

	public InorderPrinter(BinaryTreeInfo tree) {
		super(tree);
	}

	@Override
	public String printString() {
		StringBuilder string = new StringBuilder(
				printString(tree.root(), "", "", ""));
		string.deleteCharAt(string.length() - 1);
		return string.toString();
	}

	/**
	 * 生成node节点的字符串
	 * @param nodePrefix node那一行的前缀字符串
	 * @param leftPrefix node整棵左子树的前缀字符串
	 * @param rightPrefix node整棵右子树的前缀字符串
	 * @return
	 */
	private String printString(
			Object node,
			String nodePrefix,
			String leftPrefix,
			String rightPrefix) {
		Object left = tree.left(node);
		Object right = tree.right(node);
		String string = tree.string(node).toString();

		int length = string.length();
		if (length % 2 == 0) {
			length--;
		}
		length >>= 1;

		String nodeString = "";
		if (right != null) {
			rightPrefix += Strings.blank(length);
			nodeString += printString(right, 
					rightPrefix + rightAppend, 
					rightPrefix + lineAppend, 
					rightPrefix + blankAppend);
		}
		nodeString += nodePrefix + string + "\n";
		if (left != null) {
			leftPrefix += Strings.blank(length);
			nodeString += printString(left, 
					leftPrefix + leftAppend, 
					leftPrefix + blankAppend, 
					leftPrefix + lineAppend);
		}
		return nodeString;
	}
}

LevelOrderPrinter

package redblacktree;

import java.util.*;

/**

   ┌───381────┐
   │          │
┌─12─┐     ┌─410─┐
│    │     │     │
9  ┌─40─┐ 394 ┌─540─┐
   │    │     │     │
  35 ┌─190 ┌─476 ┌─760─┐
     │     │     │     │
    146   445   600   800
 */
public class LevelOrderPrinter extends Printer {
	/**
	 * 节点之间允许的最小间距（最小只能填1）
	 */
	private static final int MIN_SPACE = 1;
	private Node root;
	private int minX;
	private int maxWidth;
	private List<List<Node>> nodes;

	public LevelOrderPrinter(BinaryTreeInfo tree) {
		super(tree);
		
		root = new Node(tree.root(), tree);
		maxWidth = root.width;
	}

	@Override
	public String printString() {
		// nodes用来存放所有的节点
		nodes = new ArrayList<>();
		
		fillNodes();
		cleanNodes();
		compressNodes();
		addLineNodes();
		
		int rowCount = nodes.size();

		// 构建字符串
		StringBuilder string = new StringBuilder();
		for (int i = 0; i < rowCount; i++) {
			if (i != 0) {
				string.append("\n");
			}

			List<Node> rowNodes = nodes.get(i);
			StringBuilder rowSb = new StringBuilder();
			for (Node node : rowNodes) {
				int leftSpace = node.x - rowSb.length() - minX;
				rowSb.append(Strings.blank(leftSpace));
				rowSb.append(node.string);
			}

			string.append(rowSb);
		}

		return string.toString();
	}

	/**
	 * 添加一个元素节点
	 */
	private Node addNode(List<Node> nodes, Object btNode) {
		Node node = null;
		if (btNode != null) {
			node = new Node(btNode, tree);
			maxWidth = Math.max(maxWidth, node.width);
			nodes.add(node);
		} else {
			nodes.add(null);
		}
		return node;
	}

	/**
	 * 以满二叉树的形式填充节点
	 */
	private void fillNodes() {
		// 第一行
		List<Node> firstRowNodes = new ArrayList<>();
		firstRowNodes.add(root);
		nodes.add(firstRowNodes);

		// 其他行
		while (true) {
			List<Node> preRowNodes = nodes.get(nodes.size() - 1);
			List<Node> rowNodes = new ArrayList<>();

			boolean notNull = false;
			for (Node node : preRowNodes) {
				if (node == null) {
					rowNodes.add(null);
					rowNodes.add(null);
				} else {
					Node left = addNode(rowNodes, tree.left(node.btNode));
					if (left != null) {
						node.left = left;
						left.parent = node;
						notNull = true;
					}

					Node right = addNode(rowNodes, tree.right(node.btNode));
					if (right != null) {
						node.right = right;
						right.parent = node;
						notNull = true;
					}
				}
			}

			// 全是null，就退出
			if (!notNull) break;
			nodes.add(rowNodes);
		}
	}

	/**
	 * 删除全部null、更新节点的坐标
	 */
	private void cleanNodes() {
		int rowCount = nodes.size();
		if (rowCount < 2) return;

		// 最后一行的节点数量
		int lastRowNodeCount = nodes.get(rowCount - 1).size();

		// 每个节点之间的间距
		int nodeSpace = maxWidth + 2;

		// 最后一行的长度
		int lastRowLength = lastRowNodeCount * maxWidth 
				+ nodeSpace * (lastRowNodeCount - 1);

		// 空集合
		Collection<Object> nullSet = Collections.singleton(null);

		for (int i = 0; i < rowCount; i++) {
			List<Node> rowNodes = nodes.get(i);

			int rowNodeCount = rowNodes.size();
			// 节点左右两边的间距
			int allSpace = lastRowLength - (rowNodeCount - 1) * nodeSpace;
			int cornerSpace = allSpace / rowNodeCount - maxWidth;
			cornerSpace >>= 1;

			int rowLength = 0;
			for (int j = 0; j < rowNodeCount; j++) {
				if (j != 0) {
					// 每个节点之间的间距
					rowLength += nodeSpace;
				}
				rowLength += cornerSpace;
				Node node = rowNodes.get(j);
				if (node != null) {
					// 居中（由于奇偶数的问题，可能有1个符号的误差）
					int deltaX = (maxWidth - node.width) >> 1;
					node.x = rowLength + deltaX;
					node.y = i;
				}
				rowLength += maxWidth;
				rowLength += cornerSpace;
			}
			// 删除所有的null
			rowNodes.removeAll(nullSet);
		}
	}

	/**
	 * 压缩空格
	 */
	private void compressNodes() {
		int rowCount = nodes.size();
		if (rowCount < 2) return;

		for (int i = rowCount - 2; i >= 0; i--) {
			List<Node> rowNodes = nodes.get(i);
			for (Node node : rowNodes) {
				Node left = node.left;
				Node right = node.right;
				if (left == null && right == null) continue;
				if (left != null && right != null) {
					// 让左右节点对称
					node.balance(left, right);

					// left和right之间可以挪动的最小间距
					int leftEmpty = node.leftBoundEmptyLength();
					int rightEmpty = node.rightBoundEmptyLength();
					int empty = Math.min(leftEmpty, rightEmpty);
					empty = Math.min(empty, (right.x - left.rightX()) >> 1);

					// left、right的子节点之间可以挪动的最小间距
					int space = left.minLevelSpaceToRight(right) - MIN_SPACE;
					space = Math.min(space >> 1, empty);

					// left、right往中间挪动
					if (space > 0) {
						left.translateX(space);
						right.translateX(-space);
					}

					// 继续挪动
					space = left.minLevelSpaceToRight(right) - MIN_SPACE;
					if (space < 1) continue;

					// 可以继续挪动的间距
					leftEmpty = node.leftBoundEmptyLength();
					rightEmpty = node.rightBoundEmptyLength();
					if (leftEmpty < 1 && rightEmpty < 1) continue;

					if (leftEmpty > rightEmpty) {
						left.translateX(Math.min(leftEmpty, space));
					} else {
						right.translateX(-Math.min(rightEmpty, space));
					}
				} else if (left != null) {
					left.translateX(node.leftBoundEmptyLength());
				} else { // right != null
					right.translateX(-node.rightBoundEmptyLength());
				}
			}
		}
	}
	
	private void addXLineNode(List<Node> curRow, Node parent, int x) {
		Node line = new Node("─");
		line.x = x;
		line.y = parent.y;
		curRow.add(line);
	}

	private Node addLineNode(List<Node> curRow, List<Node> nextRow, Node parent, Node child) {
		if (child == null) return null;

		Node top = null;
		int topX = child.topLineX();
		if (child == parent.left) {
			top = new Node("┌");
			curRow.add(top);

			for (int x = topX + 1; x < parent.x; x++) {
				addXLineNode(curRow, parent, x);
			}
		} else {
			for (int x = parent.rightX(); x < topX; x++) {
				addXLineNode(curRow, parent, x);
			}

			top = new Node("┐");
			curRow.add(top);
		}

		// 坐标
		top.x = topX;
		top.y = parent.y;
		child.y = parent.y + 2;
		minX = Math.min(minX, child.x);

		// 竖线
		Node bottom = new Node("│");
		bottom.x = topX;
		bottom.y = parent.y + 1;
		nextRow.add(bottom);

		return top;
	}

	private void addLineNodes() {
		List<List<Node>> newNodes = new ArrayList<>();

		int rowCount = nodes.size();
		if (rowCount < 2) return;

		minX = root.x;

		for (int i = 0; i < rowCount; i++) {
			List<Node> rowNodes = nodes.get(i);
			if (i == rowCount - 1) {
				newNodes.add(rowNodes);
				continue;
			}

			List<Node> newRowNodes = new ArrayList<>();
			newNodes.add(newRowNodes);

			List<Node> lineNodes = new ArrayList<>();
			newNodes.add(lineNodes);
			for (Node node : rowNodes) {
				addLineNode(newRowNodes, lineNodes, node, node.left);
				newRowNodes.add(node);
				addLineNode(newRowNodes, lineNodes, node, node.right);
			}
		}

		nodes.clear();
		nodes.addAll(newNodes);
	}

	private static class Node {
		/**
		 * 顶部符号距离父节点的最小距离（最小能填0）
		 */
		private static final int TOP_LINE_SPACE = 1;

		Object btNode;
		Node left;
		Node right;
		Node parent;
		/**
		 * 首字符的位置
		 */
		int x;
		int y;
		int treeHeight;
		String string;
		int width;

		private void init(String string) {
			string = (string == null) ? "null" : string;
			string = string.isEmpty() ? " " : string;

			width = string.length();
			this.string = string;
		}

		public Node(String string) {
			init(string);
		}

		public Node(Object btNode, BinaryTreeInfo opetaion) {
			init(opetaion.string(btNode).toString());

			this.btNode = btNode;
		}

		/**
		 * 顶部方向字符的X（极其重要）
		 * 
		 * @return
		 */
		private int topLineX() {
			// 宽度的一半
			int delta = width;
			if (delta % 2 == 0) {
				delta--;
			}
			delta >>= 1;

			if (parent != null && this == parent.left) {
				return rightX() - 1 - delta;
			} else {
				return x + delta;
			}
		}

		/**
		 * 右边界的位置（rightX 或者 右子节点topLineX的下一个位置）（极其重要）
		 */
		private int rightBound() {
			if (right == null) return rightX();
			return right.topLineX() + 1;
		}

		/**
		 * 左边界的位置（x 或者 左子节点topLineX）（极其重要）
		 */
		private int leftBound() {
			if (left == null) return x;
			return left.topLineX();
		}

		/**
		 * x ~ 左边界之间的长度（包括左边界字符）
		 * 
		 * @return
		 */
		private int leftBoundLength() {
			return x - leftBound();
		}

		/**
		 * rightX ~ 右边界之间的长度（包括右边界字符）
		 * 
		 * @return
		 */
		private int rightBoundLength() {
			return rightBound() - rightX();
		}

		/**
		 * 左边界可以清空的长度
		 * 
		 * @return
		 */
		private int leftBoundEmptyLength() {
			return leftBoundLength() - 1 - TOP_LINE_SPACE;
		}

		/**
		 * 右边界可以清空的长度
		 * 
		 * @return
		 */
		private int rightBoundEmptyLength() {
			return rightBoundLength() - 1 - TOP_LINE_SPACE;
		}

		/**
		 * 让left和right基于this对称
		 */
		private void balance(Node left, Node right) {
			if (left == null || right == null) return;
			// 【left的尾字符】与【this的首字符】之间的间距
			int deltaLeft = x - left.rightX();
			// 【this的尾字符】与【this的首字符】之间的间距
			int deltaRight = right.x - rightX();

			int delta = Math.max(deltaLeft, deltaRight);
			int newRightX = rightX() + delta;
			right.translateX(newRightX - right.x);

			int newLeftX = x - delta - left.width;
			left.translateX(newLeftX - left.x);
		}

		private int treeHeight(Node node) {
			if (node == null) return 0;
			if (node.treeHeight != 0) return node.treeHeight;
			node.treeHeight = 1 + Math.max(
					treeHeight(node.left), treeHeight(node.right));
			return node.treeHeight;
		}

		/**
		 * 和右节点之间的最小层级距离
		 */
		private int minLevelSpaceToRight(Node right) {
			int thisHeight = treeHeight(this);
			int rightHeight = treeHeight(right);
			int minSpace = Integer.MAX_VALUE;
			for (int i = 0; i < thisHeight && i < rightHeight; i++) {
				int space = right.levelInfo(i).leftX 
						- this.levelInfo(i).rightX;
				minSpace = Math.min(minSpace, space);
			}
			return minSpace;
		}

		private LevelInfo levelInfo(int level) {
			if (level < 0) return null;
			int levelY = y + level;
			if (level >= treeHeight(this)) return null;

			List<Node> list = new ArrayList<>();
			Queue<Node> queue = new LinkedList<>();
			queue.offer(this);

			// 层序遍历找出第level行的所有节点
			while (!queue.isEmpty()) {
				Node node = queue.poll();
				if (levelY == node.y) {
					list.add(node);
				} else if (node.y > levelY) break;

				if (node.left != null) {
					queue.offer(node.left);
				}
				if (node.right != null) {
					queue.offer(node.right);
				}
			}

			Node left = list.get(0);
			Node right = list.get(list.size() - 1);
			return new LevelInfo(left, right);
		}

		/**
		 * 尾字符的下一个位置
		 */
		public int rightX() {
			return x + width;
		}

		public void translateX(int deltaX) {
			if (deltaX == 0) return;
			x += deltaX;

			// 如果是LineNode
			if (btNode == null) return;

			if (left != null) {
				left.translateX(deltaX);
			}
			if (right != null) {
				right.translateX(deltaX);
			}
		}
	}

	private static class LevelInfo {
		int leftX;
		int rightX;

		public LevelInfo(Node left, Node right) {
			this.leftX = left.leftBound();
			this.rightX = right.rightBound();
		}
	}
}

Printer

package redblacktree;

public abstract class Printer {
	/**
	 * 二叉树的基本信息
	 */
	protected BinaryTreeInfo tree;
	
	public Printer(BinaryTreeInfo tree) {
		this.tree = tree;
	}
	
	/**
	 * 生成打印的字符串
	 */
	public abstract String printString();
	
	/**
	 * 打印后换行
	 */
	public void println() {
		print();
		System.out.println();
	}
	
	/**
	 * 打印
	 */
	public void print() {
		System.out.print(printString());
	}
}

Strings

package redblacktree;

public class Strings {
	public static String repeat(String string, int count) {
		if (string == null) return null;
		
		StringBuilder builder = new StringBuilder();
		while (count-- > 0) {
			builder.append(string);
		}
		return builder.toString();
	}
	
	public static String blank(int length) {
		if (length < 0) return null;
		if (length == 0) return "";
		return String.format("%" + length + "s", "");
	}
}

总结

这个实现过程比较复杂，更多的是在提现一个打印结果的实现，没有必要自己去手敲，可以全部拿下来，去运行，看具体核心实现红黑树对应的那些功能。对于红黑树更细节的去使用，我也还在探索中，之后会更加细节的去记录。

ps:计划每日更新一篇博客，今日2023-05-05，日更第十九天。
昨日更新：
B树（B-tree、B-树）理论详解