剑指offer Python题解在更

LeetCode 开放了剑指相关题目
寒假延长，静心刷题。
武汉加油！！中国加油！！

1.面试题03：数组中重复的数字

解法一：Hash表法、字典法、散列表

• 用作查找（DNS查找）
• 防止重复
• 缓存（搜索引擎中使用）

class Solution:
    def findRepeatNumber(self, nums: List[int]) -> int:
        dic={} # 创建空字典
        for i in nums: # 循环数组元素
            if i not in dic: # 字典中无该元素时
                dic[i]=1
            else:
                return i
        #         dic[i]+=1
        # for k,v in dic.items(): # 循环字典判断重读元素
        #     if v>=2:
        #         return k

解法二： 排序法：先排序再查找重复元素
解法三： 顺序表法：桶的思想 + 抽屉原理
由于数组元素的值都在指定的范围内，这个范围恰恰好与数组的下标可以一一对应；
因此看到数值，就可以知道它应该放在什么位置，这里 nums[i] 应该放在下标为 i 的位置上，就根据这一点解题，这种思想与桶排序、哈希表的思想是一致的；

注意事项：
在解决该题时，想用Python 内置set函数的补集的思路求解 但set集合，只能存储不重复的元素，故该法不行。

2.面试题04. 二维数组中的查找

解法一：暴力法： 每行视为一行有序数组，对有序数组进行二分查找即可。

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        for i in range(len(matrix)):  #循环遍历所有行，对每行进行二分查找
            left=0
            right=len(matrix[i])-1
            while left<=right:
                mid=left+(right-left+1)//2
                value=matrix[i][mid]
                if value==target:
                    return True
                elif value>target:
                    right=mid-1
                else:
                    left=mid+1
        return False
    #  if target in matrix[i]:  # 不用二分法 直接判断 代码的时间复杂度最高
   	#			rerurn True
   	#	rerurn False

Notes：二分查找到的通用格式（减治的思想）

解法二： 分析矩阵规律，从右上角或者左下角开始，
（1）右上角开始时：
当右上角的元素等于目标元素时，返回true；
当右上角的元素比目标元素大时 ，剔除该元素所在的列；
当右上角的元素比目标元素小时，剔除该元素所在的行。

		if matrix==[]:  # 判断是否为空数组
            return False
        x,y=0,len(matrix[0])-1
        while x < len(matrix) and y>=0:
            if matrix[x][y]==target:
                return True
            elif matrix[x][y]>target:
                y-=1    # 剔除所在列
            else:
                x+=1    # 剔除所在行

（2）从左下角开始：
当左下角的元素等于目标元素时，返回True；
当左下角的元素大于目标元素时，剔除该元素所在的行；
当左下角的玄素小于目标元素时，剔除该元素所在的列。

3.面试题05. 替换空格

class Solution:
    def replaceSpace(self, s: str) -> str:
        # return s.replace(' ','%20') # 使用Python replace函数一行实现该功能
        snew = ''  # 开辟新的空间 循环添加
        for text in s:
            if text == ' ':
                snew += '%20'
            else:
                snew += text
        return snew

Notes：字符串不同于列表，可迭代但是不可更改。

4.面试题06. 从尾到头打印链表

解法一：栈

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        # # 用栈（数组）的思想解决该问题
         p=head
         stack=[]
         while head is not None:
             stack.append(head.val)
             head=head.next
         return list(reversed(stack))
         # return stack[::-1] # 列表的倒叙           

解法二：递归

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        if head==None:
            return []
        res = self.reversePrint(head.next)
        res.append(head.val)
        return res

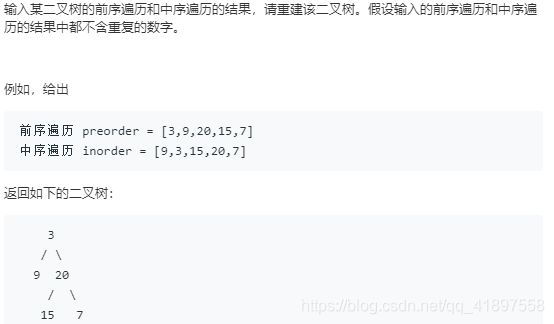
5.面试题07. 重建二叉树

解法一：递归，前中序遍历中 左右子树与根节点的关系

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if len(preorder)==0:
            return None
        mid=preorder[0]      # 找出根节点在前序遍历中的索引值 就是第一个元素
        i=inorder.index(mid) # 找出根节点在中序遍历序列中的索引值
        root=TreeNode(mid) # 创建二叉树的根节点
        root.left=self.buildTree(preorder[1:i+1],inorder[:i]) # 创建二叉树的左子树
        root.right=self.buildTree(preorder[i+1:],inorder[i+1:]) # 创建二叉树的右子树
        return root

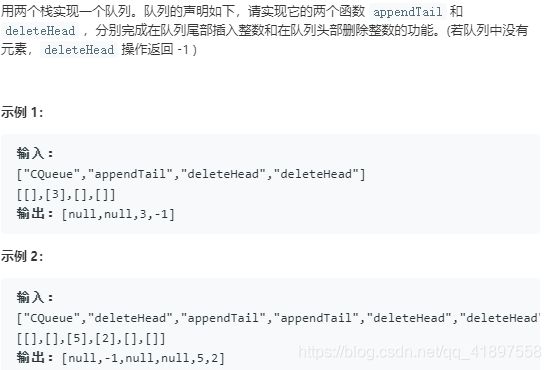
6.面试题09. 用两个栈实现对列

class CQueue:
    def __init__(self):
        self.stack1=list()   # 创建空数组 作为栈 栈1用来append
        self.stack2=list()	 # 栈2 用来del 首个元素
    def appendTail(self, value: int) -> None:
        self.stack1.append(value)
    def deleteHead(self) -> int:
        if self.stack2:      # 当栈2 有元素时就pop
            return self.stack2.pop()
        while self.stack1:   # 将栈1的元素在栈2中倒叙实现
            self.stack2.append(self.stack1.pop())
        if not self.stack2:
            return -1        # 栈2 玄素为空时 返回-1
        return self.stack2.pop()
# Your CQueue object will be instantiated and called as such:
# obj = CQueue()
# obj.appendTail(value)
# param_2 = obj.deleteHead()

TODO: 待实现用双向队列 deque实现

class CQueue:
    def __init__(self):
        self.d=collections.deque()  #collection.deque模块可以实现双向队列的操作
    def appendTail(self, value: int) -> None:
        self.d.append(value)
    def deleteHead(self) -> int:
        if not self.d:
            return -1
        else:
            return self.d.popleft()

7.面试题10- I. 斐波那契数列

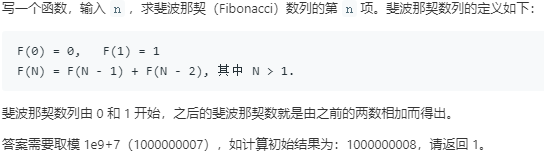
解法一：递归
Note：
递归运算：当计算到n=25左右时，代码就会超时，为解决该问题，开辟一个单独的哈希表，用来存储已经计算过的值，避免重复计算
或者，调用Python内置模块functools.lru_cache(缓存修饰器)可以实现上功能而不用另外开辟空间

# from functools import lru_cache  # 采用Python标准库的算法
class Solution:
    # # @lru_cache(None)
    # visited={}                    # 另外开辟空间的算法
    # def fib(self, n: int) -> int:
    #     if n < 2:
    #         return n
    #     if n in self.visited:
    #         return self.visited[n]
    #     else:
    #         self.visited[n] = (self.fib(n-1)+self.fib(n-2))%(1000000007)   # 注意不能使用科学计数法，否则会产生浮点数
    #     return self.visited[n]

解法二：迭代法

class Solution:
    def fib(self, n: int) -> int:      
        a = 0
        b = 1
        for i in range(n):
            a, b = b, a+b
        threshold = 1000000007
        return a % threshold

TODO：动态规划（DP）的方法

8.面试题10- II. 青蛙跳台阶问题

该题是斐波那契数列的变体，只是数列的初始条件不同。F(0)=1,F(1)=1.

解法同样如上题：递归，迭代，动态规划的方法

class Solution:
    # visted={}        # 递归的算法
    # def numWays(self, n: int) -> int:
    #     if n<2:
    #         return 1
    #     if n in self.visted:
    #         return self.visted[n]
    #     self.visted[n]=(self.numWays(n-1)+self.numWays(n-2))%1000000007
    #     return self.visted[n]
    def numWays(self, n: int) -> int:  # 动态规划的方法
        dp = {}
        dp[0] = 1
        dp[1] = 1
        if n > 1:
            for i in range(2,n+1):
                dp[i] = dp[i-1] + dp[i-2]         
        return dp[n]%1000000007

9.面试题11. 旋转数组的最小数字

刚刚开始拿到这道题，emm…讲了个啥啊 硬生生没看懂，找最小值？
一行不就可以了吗，return min(nums)提交一下竟然过了，后来转念一想，题目给你个有序数组干嘛，还旋转，再说好像时间复杂度有点高。有序数组，登登登。。。当然是二分查找了 分治法的经典应用。

class Solution:
    def minArray(self, numbers: List[int]) -> int:
         # # return min(numbers)  # 旋转数组的最小数字 二分法去解，但二分法需要        
        # # numbers.sort()       # 好吧 这个用时更多
        # # return numbers[0]
        # #二分查找法
        left=0
        right=len(numbers)-1
        while left<right:
            mid=(right+left)//2    # 取左下标
            if numbers[mid]>numbers[right]: # 当中间数大于右边数 去除掉左边数 搜索空间[mid+1,right]
                left=mid+1
            elif numbers[mid]==numbers[right]: # 相等时 只能排除掉右边元素 搜索空间[left,right-1]
                right-=1
            else:                              # 小于时 排除右边元素搜索空间[left,mid]
                right=mid
        return numbers[right]

10.面试题12. 矩阵中的路径

解法：DFS算法（深度优先搜索）/ 回溯算法：算法介绍：BFS,DFS
（1）外层循环：
首先循环遍历，矩阵表，找到与word第一个元素相同的元素(i,j)，并且在mark矩阵中将该元素置1，表示已经搜索过。
（2）内部递归：
找到第一个元素(i,j)后，搜索该元素的上下左右方向：

• 若找到下一个元素满足：board[cur_i][cur_j]==word[0],就一直重复该迭代过程
• 若找不到该元素，return False 返回外部循环 mark矩阵置0，继续遍历查找下一个元素。

class Solution:
    directions=[(0,1),(0,-1),(1,0),(-1,0)] # 搜索方向的设置 顺序无关
    def exist(self, board: List[List[str]], word: str) -> bool:
        n = len(board) # 矩阵的宽 board[0] 矩阵的长
        if n == 0:     # 矩阵没有时
            return False
        if len(word) == 0: # 所要搜索的路径为空时
            return True
        mark = [[0 for _ in range(len(board[0]))] for _ in range(n)] #创建和board相同size大小的矩阵 用来判断 是否搜索过
        for i in range(n):
            for j in range(len(board[0])): 
                if board[i][j] == word[0]: # 在board中搜索第一个元素，如果在就在mark矩阵中置1
                    mark[i][j]=1
                    if self.BFS(board,word[1:],i,j,mark) == True: # 进入深度优先搜索（BFS）回溯算法中，进行递归运算
                        return True
                    else: # 未搜索到 搜索路径回置0
                        mark[i][j] = 0

    def BFS(self,board,word,i,j,mark): # 深度优先搜索算法 回溯算法
        if len(word)==0:   # 终止条件 word中的路径遍历完
            return True
        for direction in self.directions: # 方向的设置
            cur_i=i+direction[0]
            cur_j=j+direction[1]
            if cur_i>=0 and cur_i<len(board) and cur_j>=0 and cur_j<len(board[0]) and board[cur_i][cur_j] == word[0]: # 递归条件（边界条件的设置）
                if mark[cur_i][cur_j]==1: # 若是已经搜索过就跳过
                    continue
                mark[cur_i][cur_j]=1 # 路径置1
                if self.BFS(board,word[1:],cur_i,cur_j,mark)==True: # 递归运算
                    return True
                else: # 判断为false说明路径不通，跳出递归调用时搜索路径置0
                    mark[cur_i][cur_j]=0
        return False

面试题15. 二进制中1的个数

请实现一个函数，输入一个整数，输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。
示例 1：
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

该题可以用python中自带的bin()和count()模块。
同时该题考察python中的位运算。按位与&，有0即0.
有关于Python位运算的相关应用和技术，参看文章

class Solution:
    def hammingWeight(self, n: int) -> int:
        # return str(bin(n).count('1'))
        # a=n
        # listb=[]
        # while a>=1:
        #     a,b=divmod(a,2)
        #     listb.append(b)
        # return listb.count(1)
        # 位运算 按位与&
        res=0
        while n:
            res+=n&1  #按位与 有0即0
            n>>=1     # 左移位
        return res

16. 面试题18. 删除链表的节点

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

头节点的使用可以避免特殊情况即要删除节点在头部的情况

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
        dummy=ListNode(None)
        dummy.next=head
        pre,cur=dummy,dummy.next
        while cur:
            if cur.val==val:
                pre.next=cur.next
                return dummy.next
            cur=cur.next
            pre=pre.next

20. 面试题22. 链表中倒数第k个节点

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有6个节点，从头节点开始，它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
        #解法一：遍历链表计算链表长度
        # size=0
        # tmp=head
        # while tmp:
        #     tmp=tmp.next
        #     size+=1
        # # print(size)
        # for _ in range(size-k): # 遍历到倒数第k个节点
        #     head = head.next
        # return head
        #解法二：用双指针去做，两指针相隔距离为k，则当后面指针为None时，前面指针为所求
        pre,cur=head,head
        for _ in range(k):
            cur = cur.next
        while cur:
            cur=cur.next
            pre=pre.next
        return pre

22. 面试题24. 反转链表

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

**两种解法：**双指针以及额外空间（栈）

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        # #解法一：额外空间法
        # stack=[]
        # aid=head
        # aid2=head
        # while aid:
        #     stack.append(aid.val)
        #     aid=aid.next
        # while aid2:
        #     aid2.val=stack.pop()
        #     aid2=aid2.next
        # return head
        #解法二：双指针 双指针画一下
        pre=None
        cur=head
        while cur :
            tmp=cur.next   # 借用外部空间存储cur的next节点 以便对cur.next进行赋值
            cur.next=pre           
            pre=cur
            cur=tmp
        return pre     # return的值要好好考虑           

23. 面试题25. 合并两个排序的链表

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。
示例1：
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

解题思路： 确定一个头结点dummy，在节点基础上创建新的链表，最后return dummy.next即可。cur说明在新链表中节点的当前位置。
链表题求解时，注意头节点dummy，双指针pre,cur，next，val的应用，要分清楚指针和链表的区别！！

#Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        #确定一个头结点
        dummy=ListNode(0)
        cur=dummy
        while l1 and l2: ##cur相当于指针 用来说明现在链表处理的位置 链表题 勿忘指针的应用
            if l1.val >= l2.val:
                cur.next=l2
                l2=l2.next 
                cur=cur.next
            else:
                cur.next=l1
                l1=l1.next
                cur=cur.next
        cur.next=l1 if l1 else l2 # 当l1或者l2遍历完之后，将剩余的链表放到新链表的后面
        return dummy.next

面试题26. 树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构， 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/
4 5
/
1 2
给定的树 B：
4
/
1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

若树 B是树 A 的子结构，则子结构的根节点可能为树 A的任意一个节点。因此，判断树 B是否是树 A的子结构，需完成以下两步工作：

1. 先序遍历树 A 中的每个节点 n_An （对应函数 isSubStructure(A, B)）
2. 判断树 A 中 以 n_An 为根节点的子树 是否包含树 B 。（对应函数 recur(A, B)）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        if A == None or B == None:
            return False
        # 其实是在先序遍历 然后判断每一个根节点
        return self.dfs(A,B) or self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B)  
    
    def dfs(self, A: TreeNode, B: TreeNode) -> bool:
        if B == None:
            return True
        if A == None:
            return False
        return A.val == B.val and self.dfs(A.left,B.left) and self.dfs(A.right,B.right)

27. 面试题29. 顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 2：
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

解法：设置好边界以及退出条件

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        # 设置矩阵的四个边界 每条边打印完  边界向内收缩 当左右 上下两边届相撞时 break
        if not matrix: return []
        l, r, t, b, res = 0, len(matrix[0]) - 1, 0, len(matrix) - 1, []
        while True:
            for i in range(l, r + 1): res.append(matrix[t][i]) # left to right 上边界
            t += 1
            if t > b: break
            for i in range(t, b + 1): res.append(matrix[i][r]) # top to bottom 右边界
            r -= 1
            if l > r: break
            for i in range(r, l - 1, -1): res.append(matrix[b][i]) # right to left 下边界逆序
            b -= 1
            if t > b: break
            for i in range(b, t - 1, -1): res.append(matrix[i][l]) # bottom to top 左边界逆序
            l += 1
            if l > r: break
        return res

28.面试题30. 包含min函数的栈

题目描述：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

解法： 实现栈的数据结构，列表即可，但本题的解题点在于实现min()函数的O(1)复杂度
思路： 借用辅助栈（列表），当push的元素比辅助栈内元素小时，将其push到辅助栈内，pop元素时，同样要进行比较，确定pop元素是否是最小元素。

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.stack=list()
        self._stack=list() # 辅助栈

    def push(self, x: int) -> None:
        self.stack.append(x)
        if len(self._stack)== 0 or self._stack[-1]>=x: # 判断辅助栈内元素与x的关系
            self._stack.append(x)
        
    def pop(self) -> None:
        a=self.stack.pop(-1)
        if a==self._stack[-1]: # pop元素时，同样要判断最小元素
            self._stack.pop(-1)
        return a

    def top(self) -> int:
        return self.stack[-1]

    def min(self) -> int:
        return self._stack[-1]

# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.min()

面试题32 - I. 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回：
[3,9,20,15,7]

树的广度优先遍历Python标准模块collections.deque
最后要判断节点是否有子节点if a.left，可以避免节点为None的情况。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
# 解法一 采用广度优先遍历 借助deque
        from collections import deque
        res=[]
        if not root: return []
        q=deque()
        q.append(root)
        while q:
            a=q.popleft()
            res.append(a.val)
            if a.left: q.append(a.left)
            if a.right: q.append(a.right)           
            # if a: 
            #     res.append(a.val)
            #     q.append(a.left)
            #     q.append(a.right)
        return res

面试题32 - II. 从上到下打印二叉树 II

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果：
[
[3],
[9,20],
[15,7]
]

分层遍历输出，需要借助额外空间tmp存储每一层的节点，遍历该层节点pop出的同时，要同时将节点的子节点添加到队列中。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        # 解法 二叉树的分层打印
        from collections import deque
        if not root: return []
        res=[]
        q=deque()
        q.append(root)
        while q:
            tmp=[]
            # 循环每一层的节点
            for _ in range(len(q)):    # pop出每一层的节点 将其放入tmp中 将每个节点的左右节点放入
                a=q.popleft()
                tmp.append(a.val)
                if a.left: q.append(a.left)
                if a.right: q.append(a.right)
            res.append(tmp)
        return res

面试题32 - III. 从上到下打印二叉树 III

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果：
[
[3],
[20,9],
[15,7]
]

该题在前两题的基础上，需要对偶数层的节点进行反转，最直接的方法是在tmp添加到res中时 判断当前res的长度，进而决定是否对tmp进行反转。
另外还要**注意便利表达式的应用，使代码简单凝练。*
*

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        # 解法 BFS
        from collections import deque 
        if not root: return []
        res=[]
        count=0
        q=deque()
        q.append(root)
        while q:
            tmp=[]
            for _ in range(len(q)):
                a=q.popleft()
                tmp.append(a.val)
                if a.left: q.append(a.left)
                if a.right: q.append(a.right)
            count+=1
            if count&1==0:
                res.append(tmp[::-1])
            else:
                res.append(tmp)
            # res.append(tmp[::-1] if len(res) % 2 else tmp)  # 直接计算res的长度 就不用对count进行计数了 便利表达式！！
        return res

面试题33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

二叉搜索树的性质
解法一： 递归
解法二：反向后序遍历 单调栈

class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
        # 解法一 递归 还原二叉搜索树 注意二叉搜索树的性质：左<根<右
        if len(postorder)==1: return True
        if postorder==[]: return True
        root=postorder[-1]
        index_right=0
        for i in range(len(postorder)):
            if postorder[i]>=root:    # 边界条件等于要判断
                index_right=i
                break
        left=postorder[:index_right]
        right=postorder[index_right:-1]
        for j in left:
            if j > root:
                return False
        for k in right:
            if k < root:
                return False
        return self.verifyPostorder(left) and self.verifyPostorder(right)
        

33. 面试题35. 复杂链表的复制

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。
示例 1：

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

• TODO: DFS以及BFS的解法

# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random
"""
class Solution:
    import copy
    def copyRandomList(self, head: 'Node') -> 'Node':
        # 单纯的调用python的copy函数调用deepcopy
        # 另外的解法是将该链表看为图 用深度优先搜索或者广度优先搜索解决 该问题后解
        return copy.deepcopy(head)

37. 面试题39. 数组中出现次数超过一半的数字

题目描述：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。

解题思路：
一、排序法
题目已知，一个数字的出现超过数组数字的一半，则排序后的数字就出现在数组的中位上。
由于sort()函数使用的是Timsort方法,一种归并方法的改进
时间复杂度为$O(nlogn)$
二、哈希表法（字典法）
统计每个数字出现的次数，寻找大于中位数的Vlaue值。

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        # dic=dict()  ##哈希表法
        # for i in nums:
        #     if i in dic:
        #         dic[i]+=1
        #     else:
        #         dic[i]=1
        # for k,v in dic.items():
        #     if v >= (len(nums)+1)//2:
        #         return k
        #         break
        nums.sort()  #排序法
        return nums[len(nums)//2]

面试题40. 最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。
示例 1：

输入：arr = [3,2,1], k = 2 输出：[1,2] 或者 [2,1]

• 做有关于堆的博客 堆排序
• 快排的代码

class Solution:
    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
# 解法一 借用堆排序
        # import heapq
        # return heapq.nsmallest(k,arr)
# 解法二 sorted函数
        # return sorted(arr)[:k]
# 解法三 sort方法
        # arr.sort()
        # return arr[:k]
# 解法四 快排
TODO

面试题41. 数据流中的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。
例如，
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构：
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

解法一：暴力法
解法二：大小堆 优先级队列 pop最大值时 对输入元素取负值 输出取负值即可 手写一下

class MedianFinder:
# 解法一：暴力法
    # def __init__(self):
    #     """
    #     initialize your data structure here.
    #     """
    #     self.stack=list()

    # def addNum(self, num: int) -> None:
    #     self.stack.append(num)
    #     self.stack.sort()

    # def findMedian(self) -> float:
    #     # return (stack[len(stack)//2]/stack[(len(stack)-1)//2]) if len(stack)&1==0 else  stack[len(stack)//2]
    #     if len(self.stack)&1==0:
    #         return (self.stack[len(self.stack)//2]+self.stack[(len(self.stack)-1)//2])/2
    #     else:
    #         return self.stack[len(self.stack)//2]
    def __init__(self):
        self.small,self.large=[],[]
    def addNum(self,num):
        if len(self.small)==len(self.large): #将num值放入small里 弹出small的最大值，将其发放入large里
            heapq.heappush(self.large,-heapq.heappushpop(self.small,-num))
        else:
            heapq.heappush(self.small,-heapq.heappushpop(self.large,num))
    
    def findMedian(self):
        # print(self.small,self.large)
        if len(self.small)==len(self.large):
            return (-self.small[0]+self.large[0])/2
        else: 
            return self.large[0]
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

面试题43. 1～n整数中1出现的次数

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。
例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

《编程之美》上这样说:

设N = abcde ,其中abcde分别为十进制中各位上的数字。
如果要计算百位上1出现的次数，它要受到3方面的影响：百位上的数字，百位以下（低位）的数字，百位以上（高位）的数字。
如果百位上数字为0，百位上可能出现1的次数由更高位决定。比如：12013，则可以知道百位以下出现1的情况可能是：100 ~ 199，1100~ 1199,2100~ 2199，，…，11100~11199，一共1200个。可以看出是由更高位数字（12）决定，并且等于更高位数字（12）乘以 当前位数（100）。注意：高位数字不包括当前位
如果百位上数字为1，百位中可能出现1的次数不仅受更高位影响还受低位影响。比如：12113，则可以知道百位受高位影响出现的情况是：100~ 199，1100~ 1199,2100~ 2199，，…，11100~ 11199，一共1200个。和上面情况一样，并且等于更高位数字（12）乘以 当前位数（100）。但同时它还受低位影响，百位出现1的情况是：12100~12113,一共14个，等于低位数字（13）+1。 注意：低位数字不包括当前数字
如果百位上数字大于1（2~ 9），则百位上出现1的情况仅由更高位决定，比如12213，则百位出现1的情况是：100~ 199,1100~ 1199，2100~ 2199，…，11100~ 11199,12100~12199,一共有1300个，并且等于更高位数字+1（12+1）乘以当前位数（100）

class Solution:
    def countDigitOne(self, n: int) -> int:
        cnt, i = 0, 1
        while i <= n: # i 依次个十百位的算，直到大于 n 为止。
            cnt += n // (i * 10) * i + min(max(n % (i * 10) - i + 1, 0), i)
            i *= 10
        return cnt

面试题44. 数字序列中某一位的数字（找规律）

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。
请写一个函数，求任意第n位对应的数字。

class Solution:
    def findNthDigit(self, n: int) -> int:
        base=9
        count=1
        # 获得n的位数
        while n-base*count>0:
            n-=base*count
            base*=10
            count+=1
        # print(n)
        a,b=divmod(n,count)
        if count==1:
            number=a
        else:
            if b==0:
                number=10**(count-1)+(a-1)
            else:
                number=10**(count-1)+(a)
        # 确定n所在的数字
        # print(count,number,a,b)
        #找出该数字
        if b==0:
            res=str(number)[-1]
        else:
            res=str(number)[b-1]
        return int(res) 

48. 面试题50. 第一个只出现一次的字符

在字符串 s 中找出第一个只出现一次的字符。如果没有，返回一个单空格

解法：
（1）创建一个哈希表，存储每个字母出现的次数，由于字典存储是无序的，故仍需遍历一遍字符串 找出第一个value值为一的值
（2）采用顺序哈希表 collections的模块collections.OrderedDict()，最后遍历字典的items找出value值为1的key值。

class Solution:
    def firstUniqChar(self, s: str) -> str:
        dic={}
        for i in s:      # 提供两种在字典中存值得方法
            # if i in dic:
            #     dic[i]+=1
            # else:
            #     dic[i]=1
            dic[i]=dic.get(i,0)+1
        # 该方法遍历速度慢 时间复杂度高 直接遍历字符串即可！
        # for k,v in dic.items():
        #     for i in s:
        #         if v==1 and i==k:
        #             return k 
        #             break
        # return " "
        for i in s:
            if dic[i]==1:
                return i
        return " "

面试题53 - I. 在排序数组中查找数字 I

统计一个数字在排序数组中出现的次数。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        # # 二分法 搜索左右边界
        left=0
        right=len(nums)-1
        while left<=right:
            mid=(left+right)>>1
            if nums[mid]<target:
                left=mid+1
            elif nums[mid]>target:
                right=mid-1
            elif nums[mid]==target: # 找到目标值后 搜索相等的左右边界
                low,high=mid,mid
                while low>=0 and nums[low]==target:
                    low-=1
                while high<=len(nums)-1 and nums[high]==target:
                    high+=1
                return high-low-1
        return 0
        # # hash table
        # dic=dict()
        # for i in nums:
        #     if i in dic:
        #         dic[i]+=1
        #     else:
        #         dic[i]=1
        # for k,v in dic.items():
        #     if k ==target:
        #         return v
        # return 0
                

面试题53 - II. 0～n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

解法一：暴力法：注意边界条件
解法二：二分法注意出口

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        # # 解法一：数组中第一个下标不符的即为缺省值 该值为下标
        # if nums[-1]==len(nums)-1:
        #     return len(nums) 
        # else:
        #     for i in range(len(nums)):
        #         if nums[i]!=i:
        #             return i
        # # 解法二：二分法
        # left=0
        # right=len(nums)       
        # while left
        #     mid=(left+right)//2
        #     if mid==nums[mid]:
        #         left=mid+1
        #     elif mid
        #         right=mid
        # return left
         # 解法二：二分法
        left=0
        right=len(nums) -1      
        while left<=right:
            mid=(left+right)>>1
            if mid==nums[mid]:
                left=mid+1
            elif mid<nums[mid]:
                right=mid-1
        return left

面试题55 - II. 平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/
9 20
/
15 7
返回 true 。

树的高度计算 递归调用max（）即可。
算法优化：在递归调用计算树的高度时 若子节点的左右子树的高度相差大于1 则直接输出False，不用计算整个树的高度，即可以不在is_banlanced函数里递归比较。只需要以此树的DFS即可。时间复杂度由nlogn可以降为n

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            return True
        if abs(self.height(root.left)-self.height(root.right))>1:
            return False
        else:
            return self.isBalanced(root.left) and self.isBalanced(root.right)

    def height(self,p): # 递归计算树的高度 可优化 计算的时候比较 
        if not p:
            return 0
        else:
            return 1+max(self.height(p.left),self.height(p.right))
        

5/0. 面试题52. 两个链表的第一个公共节点

输入两个链表，找出它们的第一个公共节点。

如下面的两个链表：

在节点 c1 开始相交。

解题思路： 暴力法以及双指针法

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        # # 暴力法 先求每个链表的长度 在计算公共长度下 节点是否相交 相交的定义是node相同 而不是val相同（地址相同）
        # sizea=0
        # sizeb=0
        # a,b=headA,headB
        # while a:
        #     a=a.next
        #     sizea+=1
        # while b:
        #     b=b.next
        #     sizeb+=1
        # a1,b1=headA,headB
        # cur=None
        # if sizea>=sizeb:
        #     for _ in range(sizea-sizeb):
        #         a1=a1.next
        # if sizea
        #     for _ in range(sizeb-sizea):
        #         b1=b1.next
        # while a1:
        #     if a1==b1:
        #         if cur == None:
        #             cur=a1
        #             a1=a1.next
        #             b1=b1.next
        #         else:
        #             a1=a1.next
        #             b1=b1.next
        #             continue
        #     if a1 != b1:
        #         cur=None
        #         a1=a1.next
        #         b1=b1.next
        # return cur
        
        # 双指针法 定义两个指针 每个指针遍历完自己链表后定位到下一个链表 一直找到节点相同的位置上
        a1,b1=headA,headB
        while a1!=b1:
            a1=a1.next if a1 else headB
            b1=b1.next if b1 else headA
        return a1

面试题58 - I. 翻转单词顺序

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student. “，则输出"student. a am I”。
示例 2：
输入: " hello world! "
输出: “world! hello”
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

要了解字符串类型str的基本操作，以及列表list切片和reversed函数的效率

class Solution:
    def reverseWords(self, s: str) -> str:
#解法一
        # res=[]
        # for i in s.split():
        #     res.append(i)
        # # res=reversed(res)         # 翻转列表使用reversed效率更高
        # world=' '.join(res[::-1])
        # return world
# 解法二
        # return " ".join(reversed(s.split())) # s.split(0) 生成的就是列表没必要迭代
# 解法三
        return " ".join(s.split()[::-1])  # reversed比切片要快的多