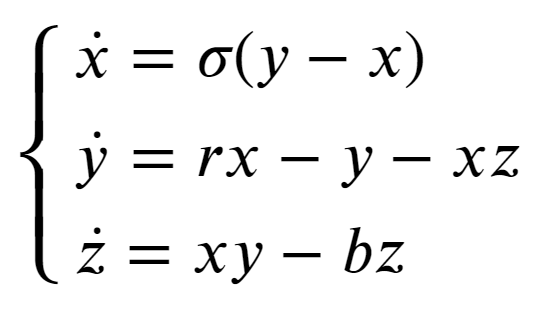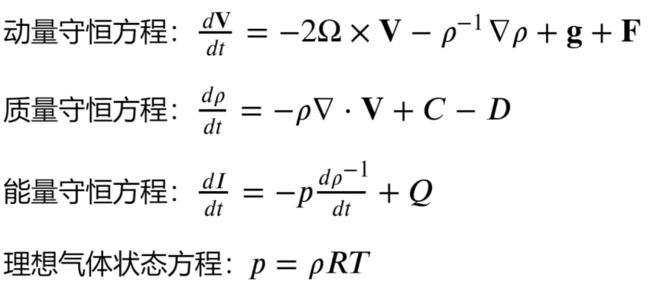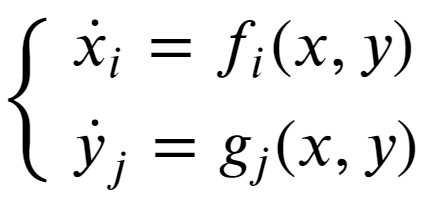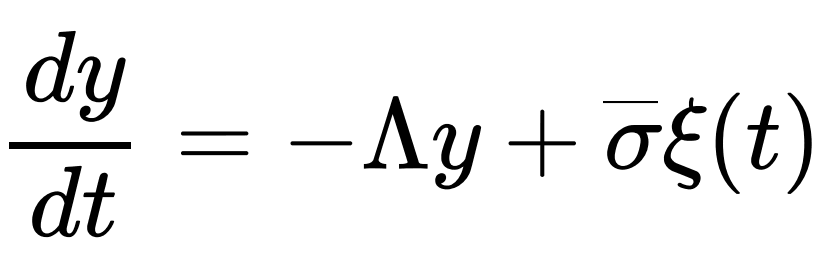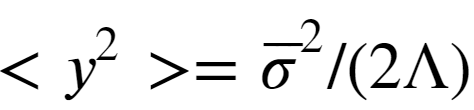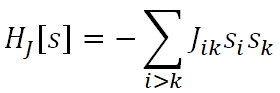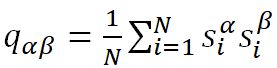复杂的世界 简单的规律 —— 2021年诺贝尔物理奖科学背景介绍及解读

2021 年诺贝尔物理学奖被授予“对我们理解复杂系统的开创性贡献”，一半授予真锅淑郎（Syukuro Manabe）和克劳斯·阿塞尔曼（Klaus Hasselmann），表彰他们“对地球气候的物理建模、量化可变性和可靠地预测全球变暖”的贡献，另一半授予乔治·帕里西（Giorgio Parisi），表彰他 “发现了从原子到行星尺度的物理系统中无序和涨落之间的相互影响”。

后面这位分享了一半奖金的科学家早在1980年就在《中国科学》杂志上发表了重要的论文[1]，这篇文章出现在当天下午举办的Nobel Prize Colloquium里，作为获奖人的重要成果进行展示。

✦ 原文中文版 ▲ 【上下滑动查看，全文链接见文后 】

✦ 原文英文版 ▲ 【上下滑动查看，全文链接见文后 】

诺奖授予“复杂系统”这是一次“破天荒”事件，很多人第一反应是“什么是复杂系统？”，“什么是混沌？”，然后是 “他们的工作为这么重要？”，“和物理有什么关系？”。因此，要解读今年的诺奖，首先需要介绍什么是复杂系统及其混沌概念。 

什么是复杂系统？

实际上复杂系统还没有统一的定义，诺奖的网站上对什么是复杂系统的描述比较具有概括性：“物理学家已经对它们进行了几个世纪的研究，由于具有大量的组成部分，或者受偶然性支配，因此很难用数学来描述复杂系统。它们可能是混沌系统，诸如天气系统，初始值的小偏差会导致后期的巨大差异。”据此，我们可以把复杂系统分为具有复杂结构的系统和具有复杂运动的系统，其各组成成分或单元之间以非线性相互作用为基本特征。简单讲，帕里西的主要工作属于研究复杂结构系统的宏观性质，真锅淑郎和阿塞尔曼的工作属于理解复杂系统的运动。          

那么复杂系统涵盖了哪些领域呢？我们知道，物理学的主要任务是认识物质世界的结构与运动，但是这个任务还没有完成。对于结构，粒子物理标准模型建立了基本粒子表，在此基础上拼装出了质子和中子，然后拼装出原子核、原子、分子，然后是固体材料、玻璃、流体、生物软物质、人体系统、大脑、天气系统、各种网络等等，再然后是地球、太阳、太阳系、银河系、星系团、宇宙。看到这串名词，你会很快认识到我们最不清楚的是中间的这一部分，这就是所谓的复杂结构系统。

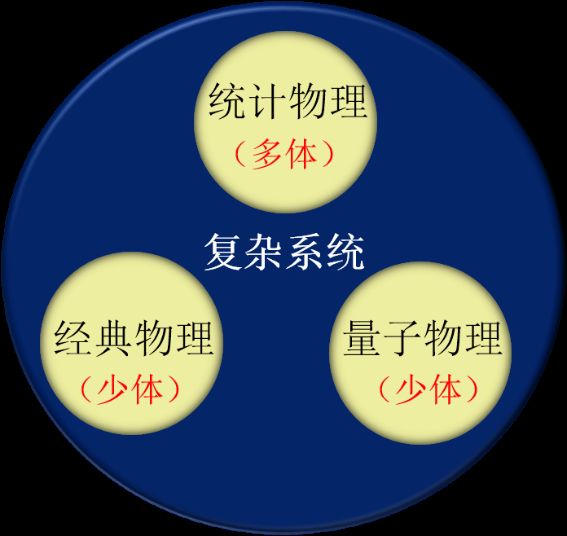
图一  复杂系统示意图

对于运动，我们建立了经典理论、量子理论、统计物理和热力学。然而，这些理论足够吗？在一定意义上讲，科学的价值在于能够提供预测能力。有了牛顿方程（高速高能情况有相对论方程）我们可以精确预测一颗行星围绕恒星的运动，也可以预测两颗恒星相互绕转的运动，但是我们可以精确预测三体的运动吗？不能，这是所谓的几个世纪的难题。有了薛定谔或海森堡方程我们能精确求解氢原子，但是能精确求解氦原子吗？不能，只能用各种微扰方法近似求解。这是为什么？因为三体及三体以上的非线性相互作用系统，存在所谓的混沌运动，一般不能解析求解。另外一个极端，也就是具有无穷多个粒子的热力学极限的系统，平衡态统计物理可以准确预测其宏观性质。但是这个理论的应用范围和工具手段也非常受限。只要粒子数量有限，统计物理就不再严格成立了。即便是无穷粒子的系统，如果相互作用是长程的，如自引力系统，这个理论也不能用了。同时，如果系统处于非马尔可夫过程或非平衡态，情况也会变得很复杂。非平衡态统计物理虽然比量子力学起源还要早，但是它却是物理学的大框架下迄今还没有被完整建立的理论。

于是，如图一所示，介于这几个理论体系之间的交叉区域都属于复杂系统的范畴，几乎包括了我们面对的大部分实际系统，覆盖自然科学乃至社会科学的各个领域。理解和预测这类系统实际上也是大部分科学家几个世纪以来（正如诺奖网页上所说的）以及目前正在从事的工作，只是近几十年才被冠以复杂系统的框架，成为一门跨越多个学科的交叉领域。当然复杂系统也不是把什么都包进来了，它所研究的是各种系统背后的共性规律，超越于具体的微观结构或微观相互作用细节，诸如各种涌现现象。一定意义上说，大部分的具体学科还是以解剖麻雀的还原论方式研究所面对的对象，而复杂系统则试图从整体上研究共性。相对于物理学天上的乌云，我们可称图一的交叉区域为地上的沼泽。如果我们暂且忽略暗能量暗物质这类大问题，不会影响大家的穿衣吃饭，但是如果忽略了这些沼泽，那就会出问题，因此我们需要一步一步地探索前行，一个城堡一个城堡地攻克。 

什么是混沌？

研究复杂系统为什么困难？这要从混沌运动说起。西方世界有个神，叫 “chaos”，是主宰战争、混乱、瘟疫的神。中国上古神话也有一个类似的神叫“混沌”，他的样子很怪异（结构无序），如 “其状如犬，长毛四足，似罴而无爪，有目而不见” (《神异经》)；“其状如黄囊，赤如丹火，六足四翼，浑敦无面目”(《山海经》)。其行为乖张不可捉摸（运动无序）：“掩义隐贼，好行凶慝”(《史记》)，“人有德行而往抵触之，有凶德则往依凭之”(《神异经》)，他因此也代表无序与混乱。可见古人在认识到春夏秋冬、斗转星移等规则运动的同时，也认识到了还存在风雨雷电、洪水猛兽等不可预测现象，于是创造了秩序之神的同时也创造了无序之神。混沌这个概念的翻译，可以说是我国老一辈学者的神来之笔。

图二  中国古籍中混沌神的形象

物理上，首先描述混沌运动的是庞加莱 (J.H. Poincaré)，他在研究三体问题时发现了同宿异宿轨道，这些轨道在不稳定的双曲点附近存在庞加莱栅栏。也就是说双曲点附近的轨道非常复杂，敏感地依赖于初值，无法预测其最终归宿。“太过复杂以至于我不想继续描述它们”，庞加莱说。这和牛顿以来大家常见的规则或周期运动不一致，这一发现被认为是混沌运动研究的开始。

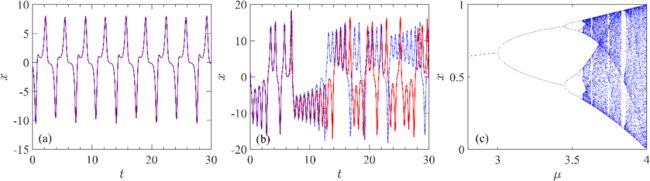
图三  混沌系统的初值敏感性。(a) 周期轨道，（b）混沌轨道，以及（c）非线性系统典型的参数空间分叉图。可见周期运动下系统对初值不敏感，混沌运动下初值敏感，表现出“短期可预测，长期不可预测” 

到 1961 年，美国数学与气象学家洛伦兹（E.N. Lorenz）利用计算机进行天气预报，据说计算到中间停机了，重新开机后他利用中间记录的数据接着计算，结果惊奇地发现预测结果和重新从头算起的结果相差巨大。经过检查，他发现这仅仅是由于中间停机后记录数据小数点后几位在接着计算时被省略了。于是他认识到了天气系统具有敏感的初值依赖性。后来他把用于实际天气预报的微分方程组简化为三维常微分方程组，得到了现在大家熟知的洛伦兹方程[2]：

这个方程在一定的参数区间表现为周期运动，而在另一些参数区间则表现为貌似随机的混沌运动。它们最显著的区别是周期运动区对初始扰动不敏感，初始距离很小的两条轨道长时间演化后两者依然差别不大，如图三(a)所示。而在混沌参数区，这两条轨道在短时间内差别不显著，而长时间后，两条轨道完全分道扬镳，互不相干，如图三(b)所示。这就是著名的蝴蝶效应：“巴西的蝴蝶拍一下翅膀，可能会在一个月后引发美国德州的龙卷风”。这一发现不仅意味着天气系统短期可预测而长期不可预测，更表明确定性的系统可以具有内在随机性，对确定论和随机论产生了全新的认识，对人们认识自然产生了深远的影响。目前，蝴蝶效应已经被很多领域，包括金融社会等领域高频使用，用来特指那些微小因素引起巨大后果的事件。然而，这同时也引发了问题：气候是否不可预测？世界上每时每刻不仅有无数的蝴蝶在煽动着翅膀，也有无数的鸟儿在煽动着翅膀飞翔，如果都引起大雨，那会是怎样的情景？

也就是说混沌之中应当还有共性的规律，有特殊的结构。1974年，May 发了一篇文章[3]，发现一个简单的非线性映射，Logistic 映射随着参数的变化竟然也展现出了非常丰富和复杂的行为。图三(c)中画出了其分岔图，也就是去掉暂态后的时间序列（每个参数下记录多个连续的x值）随参数的变化，表明系统随着参数的变化由周期1的状态演变到周期2的状态，再到周期4的状态, ...，然后进入了混沌状态，混沌区还夹杂着一系列的周期运动状态即周期窗口，如周期三窗口。这表明，简单的非线性演化系统就能表现出复杂的运动。这可不是个纯数学游戏，自然耕作年代中国的农民早就知道，有些庄稼地每年产量保持恒定，有些则出现大小年，有些更出现大年平年小年的三周期。随后在 1975 年，李天岩和 James A. Yorke 证明了周期3意味着混沌[4]，也就是说一个系统只要出现周期3，那就一定存在各种周期轨道，能够表现出混沌运动。这对看起来如此复杂的系统给出了一个非常简单和普适的判据，表明混沌是有规律可循的。这是耗散系统，对于保守系统，如三个天体的自引力系统，庞加莱之后持续的研究也认识到了这是一个典型的混沌运动系统。氦原子的研究，表明量子系统也存在混沌运动，也就是量子混沌。这样混沌运动或复杂运动被证实其实在只有几个单元的非线性相互作用系统就能发生。这和《道德经》的一生二，二生三，三生万物竟然异曲同工。 

随后人们发现了各种非常不同的非线性系统，都具有经过倍周期分岔进入混沌的特性，被叫做倍周期通向混沌之路。1975年，一头卷发高个子青年费根鲍姆（M.J. Feigenbaum）用计算器经过多年的计算后得出，这种倍周期分岔发生时的参数之间差的比值对一大类非常不同的系统是一个普适常数，。他后来于1978年用重整化群方法给出证明[5]。这些结果表明了混沌运动系统竟然具有如此普适的规律，也就是复杂的系统背后存在简单的规律。普适常数的存在大家知道意味着什么，光速—相对论，普朗克常数—量子力学，玻尔兹曼常数—热力学统计物理。至此，一门新学科混沌学正式诞生了。费根鲍姆和洛伦兹都是这个领域的标志性人物，对他们应当获得诺奖的呼声一直很高，可惜他们都等不到这一天了，特别是费根鲍姆于前年，在与很多诺奖得主相比还不算太老的75岁时不幸去世了。 

明确了在我们的世界里复杂系统是绝大多数，简单系统或可积可解的系统是凤毛麟角，那么理论物理学家的任务就没有完结，我们需要寻找复杂系统的运动规律并给出预测，给图一中的沼泽地带铺上路。然而复杂系统个性太强，需要一个城堡一个城堡的去攻克。今年的诺贝尔物理学奖获得者，真锅淑郎和阿塞尔曼拿下了一城，帕里西拿下了另一城，两城具有很高的共性，又有不同。

真锅淑郎和阿塞尔曼的工作

从统计物理的观点看，描述多体非线性相互作用的复杂系统分三个层次，即微观的分子动力学描述、介观的 Kinetic 描述或朗之万方法描述（平均场近似也是其中之一）、宏观的流体力学描述。从微观到宏观，通过近似方法不断减少系统自由度，突出主要物理过程，使得问题得以求解。这次获奖的两位气象学家可以说是成功地运用统计物理的方法和非线性动力学方法，从宏观和介观的层次求解了全球大气运动方程，使得气候变化的预测成为可能。特别是较为精确地预测了二氧化碳浓度的升高如何导致了大气温度的升高，并且定量计算了人类活动在其中扮演的角色。

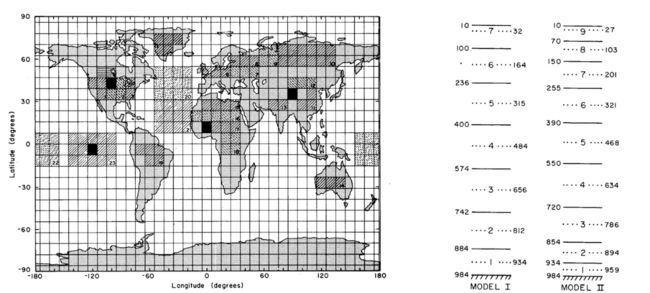
真锅淑郎自1950s 加入美国大气环流研究部以来，一直主导完善全球气候模型(Global Climate Models, GCMs)。该模型采用流体力学方法对全球范围的大气运动建模。该方法基于三个守恒方程，即动量守恒、能量守恒和质量守恒，再加上理想气体状态方程[6]，即：

这组方程描述了大气压力、密度和温度的时空变化，结果导致了著名的纳维-斯托克斯方程，解析求解该方程依然是数学上的难题。第一台电子计算机 ENIAC 的出现为数值求解成为可能。数值模型一般在地球平面上划分1000-100 km的网格，在垂直空间上划分7-9层，如图四所示。随着计算机算力的提高，网格划分的精度也不断提高。

图四  平面网格和水平分层示意图（引自文献[6]）

真锅淑郎在完善和精细化全球数值气候模型方面做出了巨大的贡献，使得该模型的预测能力极大提高。比如， 1965年在该模型中加入了水循环[7]，1967年，考虑垂直方向的湿度分布以及精确的温室气体吸收谱[8]，求解了该模型的一个垂直一维的简化模型。

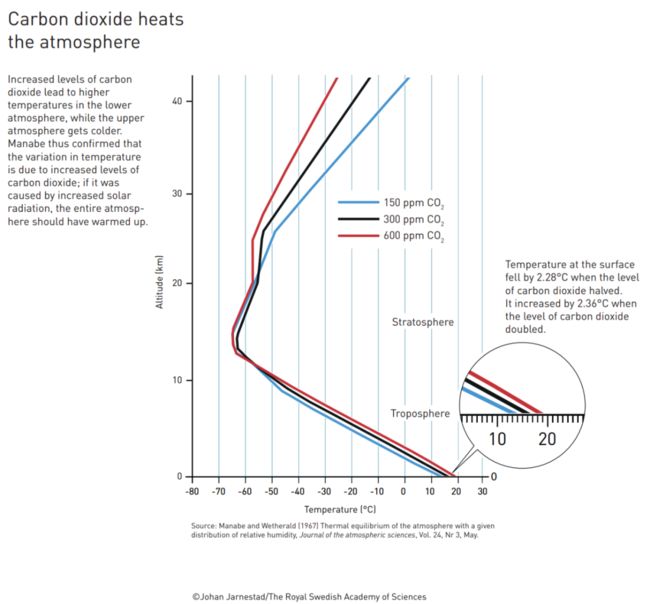
早在 1824 年法国科学家傅里叶就已经认识到了大气的温室效应。太阳入射地球表面的光被吸收后转换为红外光辐射回大气，大气漫反射留住大部分的热量，从而加热了空气使得地球有了生命宜居的条件。空气中的水是主要的温室气体，但是当时人们还不知道空气中其他各成分对温室效应的贡献。一般来说，氧气和氮气含量占绝对优势，大家并不太注意含量比重非常少的二氧化碳的贡献。真锅淑郎的贡献就在于利用他参与建立的这个模型证明了氧气和氮气的贡献几乎可以忽略，而二氧化碳的贡献非常显著，且对水蒸汽加热空气有正反馈效应。在那个完全不存在碳排放这个名词的时代，首次定量地准确预言了二氧化碳含量增加将加热地球，确实代表了科学的力量，物理的力量。

图五  不同浓度的二氧化碳（用不同颜色线表示）在不同的海拔高度上（y轴）对应的温度值（x轴）。图中放大部分清晰地显示，在地表，如果二氧化碳浓度翻倍，温度将升高 2.28 摄氏度（引自[9]）

全球气候模型研究气象观察量的统计平均，例如平均值、标准偏差、最高和最低测量值等。它可以预测某地某时的平均温度或降雨量，但是无法告诉你某地某时的天气会怎么样，比如暴雨、极寒等极端天气何时出现。正如洛伦兹模型所揭示的，天气模型是混沌系统，无法做出长期预测。这样一个混沌系统如何影响更大规模气候模型？

这就是阿塞尔曼对气候模型的贡献。他将宏观的气候变化和介观的天气变化之间的相互影响简化成如下方程[10]：

x的方程表示局部的天气变化，而y的方程表示宏观的气候变化。x的变化在更小的时空范围表现为混沌运动，具有内禀的随机性。y的变化在更大的时空范围缓慢变化。这样一种运动快慢可分离的耦合系统可以通过投影算符的方法简化，将快变量x的影响近似为具有某种统计性质的随机色噪声，这样我们就可以主要关注y的变化规律[10]：

这个方程叫朗之万方程。在这个方程里，只描述y的变化规律，而x的变化规律全部约化成了噪声项，它的变化幅度为。这种方法在物理领域最早可以追溯到 1905 爱因斯坦对布朗运动的处理，而在金融领域，可以追溯到1900年庞加莱的学生 Louis Bachelier 对商品价格的处理。

朗之万方程的求解可以得到一个重要的关系，称为涨落耗散关系。即：

这意味着我们可以定量计算噪声x的变化强度如何影响宏观气象数据y的涨落。

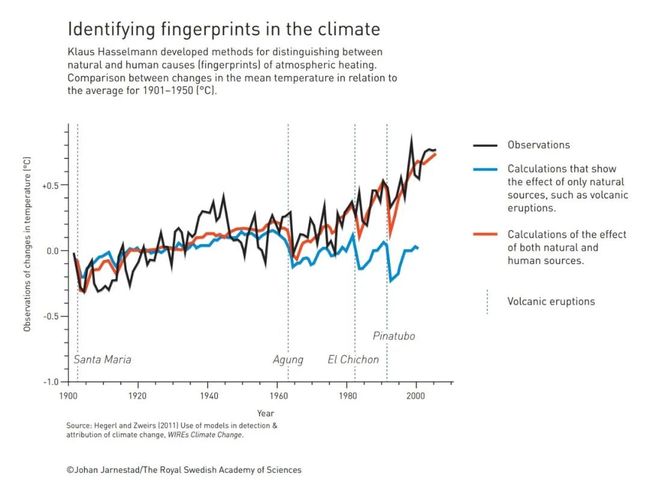
这种方法已经发展成为非平衡态统计中最重要的理论之一，即涨落理论。阿塞尔曼正是遵循这一思路，不但提高了气候模型预测精度，而且还从气候涨落数据中，分离出了自然噪声和人类活动噪声的影响，从而令人信服地揭示出了人类活动自二十世纪六十年代以来对全球变暖起主要作用。

图六  识别气候变化中的人类活动“指纹”（引自[9]）

帕里西的工作

帕里西的工作网上已经有很多详细介绍，我们这里只做简单解读。他获奖的主要工作是精确求解了具有长程相互作用的随机Ising模型，也就是Sherrington-Kirkpartick（S-K）模型，

其中s为系统的自旋构型，J_ik是随机变量，其概率分布为P[J]。如果J_ik可正可负，系统中将同时存在铁磁和反铁磁相互作用，阻挫就会出现，这时系统将存在大量的亚稳态。具体的，在S-K模型中J_ik是高斯随机数，其强度取决于系统尺寸，以保证系统的广延性。事实上，由上述哈密顿定义的系统，无论是近邻相互作用还是长程相互作用，当低于临界温度时，系统均处于宏观无序但微观有序的状态，即自旋玻璃态。自旋玻璃与普通玻璃不一样，它具有明确的热力学平衡态。

而当J_ik取相同常数且只考虑最近邻相互作用时，这个模型就回到了著名的伊辛模型。它由Wilhelm Lenz 于1920年提出，并由其学生伊辛在1924年对一维情况进行了研究。之后很多学者对二维伊辛模型进行了研究，得到了各种近似解。1944年美国物理学家拉斯·昂萨格（Lars Onsager）得到了二维伊辛模型在没有外磁场时的解析解，严格描述了其连续相变，这是统计物理微观模型被严格求解的为数不多的特例，成为研究连续相变的基础。昂萨格因此获得玻尔兹曼奖。

同样，S-K模型也吸引了众多学者的兴趣，但都没有取得真正的成功。帕里西使用了由他人已经发展起来的复本方法，其基本思想是由相同的分布函数产生很多组J_ik而构成一个个“复本”（replica），把这些复本看成等价系统（即假定复本对称）而利用复本数趋于零的技巧而获得结果。这个技巧很奇特但却能给出正确的结果。帕里西的创新之处在于他认识到自旋玻璃存在很多基态和大量自由能局域极小的态，系统一旦处于这些态就会停留非常长的时间，这些态被叫做纯态（不同于量子力学中的纯态）。在原始的伊辛模型中，这样的纯态只有两个。帕里西认为大量纯态的存在，使得复本等价的假设不再成立，因为那些原本统计上等价的复本会快速自动扎堆地演化到这些能量面局部最小或极小态。为了描述这些纯态的结构，帕里西引入了一个新的序参量，即纯态α和β的重叠度

我们知道通常的系统只需定义一个特定的序参量，而在这里被序参量谱取代，这是个革命性的概念。进而通过应用复本数趋于零的技巧，帕里西获得了复本对称破缺的解析解，由此揭示了纯态的结构及性质，特别是纯态之间具有的自相似结构。这样帕里西获得了由伊辛模型推广而来的S-K模型的解析解，在认识复杂无序系统的性质方面攻下了一城。大量纯态的存在是阻挫系统的共同特征，他的方法因此可以用来解决组合优化以及神经网络等诸多问题，为理解一大类复杂结构系统提供了理论和方法，应用价值巨大。

帕里西与中国的渊源很有趣。诺奖引文中他的一项重要的工作，KPZ方程，就是他和他的第一个博士生，中国科学技术大学毕业的张翼成以及合作者Mehran Kardar 于1986年完成的，这个方程最初是用来描述表面离散生长的连续近似，现在已经被广泛应用于非线性科学和非平衡统计物理等领域，成为物理学的一个经典方程。

而早在1980年，这位意大利的红色科学家就只身远赴红色中国支持中国的科学发展。他来到组建不久的中国科学院理论物理研究所，在简陋的条件下和中国年轻学者吴詠时完成了一篇工作“不用固定规范的微扰论”，并于第二年以中英文同时发表在了《中国科学》上[1]，这个工作已经引用过千次，成为相关领域的经典之作。

这篇工作系统地引入了一种全新的方法处理非阿贝尔规范场论中的微扰计算。在规范场理论中，由于规范场所带来的冗余自由度，人们在进行对规范不变的物理量的计算中，不得不选取一些特定的固定规范来进行计算。而在非阿贝尔规范场论中，固定规范等价于引入所谓的Faddeev-Popov 鬼场来抵消掉规范场中冗余自由度的贡献，被称为BRST量子化。由于非阿贝尔规范变换的高度非线性，这些鬼场会与规范场中的物理自由度产生复杂的相互作用。当规范场论在非微扰的区域内，会存在现被称之为Gribov ambiguity的现象，从而导致BRST量子化在非微扰的区域中失效。

尽管帕里西与吴詠时的出发点始于非阿贝尔规范场论中的微扰理论，但这篇文章对后续人们研究非阿贝规范场论中的重要非微扰问题，无论在概念还是技术层面均有着深远的影响。不同于传统场论对关联函数的直接计算，他们引入了一个额外的“时间”维度，并将4维欧氏场论延拓到这个维度成为“4+1” 维场论。这样关联函数的计算就可以通过由朗之万方程描述的随机过程所达到的平衡态而得到，避免了在可能的非微扰区域中的Gribov ambiguity。现在帕里西与吴詠时的这一量子化范式被称为随机量子化（stochastic quantization）。基于随机量子化，人们后续进行了许多规范场在非微扰物理性质的研究。其中值得一提的是非阿贝尔规范场论中著名的“色禁闭”（color confinement）问题，在随机量子化的范式以及一些假设下，可以被理解为研究各类算子关联函数的奇点问题。因此，这也将“色禁闭” 这一在低能红外区艰难的动力学问题转化为一个由非阿贝尔规范不变性所导致的运动学问题。

另一方面，这个工作也对格点规范理论中的计算问题有着重要的影响。在格点规范场论中，将量子场论放在格点上会导致其作用量S复化。在标准的关联函数的数值计算中，人们将路径积分中的exp(-S)理解为概率权重，由于作用量S的复化带来额外的相因子，传统的数值计算方法因此而失效，这就是著名的符号问题（sign problem）。而随机量子化并不依赖于上述的概率权重解释，相反地，关联函数的计算通过由朗之万方程所描述的随机过程的平衡条件给出，因此在原理上有效地规避了符号问题所带来的技术难题。近年来，在一些诸如玻色气体等同样存在符号问题的模型中，人们利用随机量子化所设计的方法有效地研究了这些模型在强关联区域的相变问题。也许在可期的将来，我们会看到格点规范场论中的符号问题由随机量子化这一思路所带来的重大突破也未可知。

帕里西从事过的研究工作非常广泛，除了这些顶级的解析工作，他也做过大量数值模拟研究，只要他认为是重要的基本问题。我们知道能量均分假设，即系统的能量会均分到每个自由度上，是统计物理的基础，但同时也是一个至今为止还没有被完全严格证明的问题，特别是对于固体模型。1954年费米带领他的研究组首次利用数值模拟研究了非线性耦合振子的能均分过程，吃惊地发现均分没有像预期那样发生，这就是著名的FPUT佯谬。在 KAM 定理的启发下，当时人们普遍认为费米他们的结果意味这系统的非线性强度存在均分阈值，阈值之下，系统保留可积性从而不会均分。1982年，帕里西等推测FPUT佯谬是由于系统高低频模式特征时间尺度相分离而导致亚稳态，长时间后系统最终会达到均分态[11]。1997年，帕里西进一步数值研究了更长的模型，表明在热力学极限下非线性耦合振子总能达到均分而否定了存在阈值的推测[12]。我们研究组有幸延续了该观点，近年来利用数学物理领域的波湍流理论作为解析工具，结合数值模拟验证，给出了从一维到三维的一般非线性晶格系统能均分时间与微扰强度的平方成反比的规律，表明足够大的系统一定能实现均分，并证明了声子无序系统中的Anderson局域模是不稳定的，可以被任意小的扰动破坏[13]。 

讨论与展望

今年诺奖获得者虽然在很多人预料之外，但想来也在情理之中。对帕里西，其工作或许不能和物理学黄金白银时代的大家们的工作相比，但即便是挑剔的理论物理学家也应当认可他工作的优美，表明原以为如此混乱无头绪的系统竟有如此简单清楚的普适结构，而且其理论和方法更可用来研究“从原子到行星尺度的物理系统中无序和涨落之间的相互影响”。不过对于帕里西，还是有人正确预言了他的获奖，只是没有想到会冠以“复杂系统”的名头。而真锅淑郎和阿塞尔曼，据说他们自己都没有想到会获奖。很多人更不理解为什么物理学奖颁发给了两个气象学家，但从我们前面的介绍可见，他们完全是用物理的思想和方法，结合实验观测给出了复杂的气候系统中确定性的运动规律，整个人类用几十年的活动证明了他们预言的结果，即气候变暖和大气中二氧化碳含量间的确切联系。这鼓励人们进一步向预测地震、冠心病等复杂系统的运动进军，攻破这些顽固的堡垒。无论如何今年的物理诺奖是个风向标，表明以后有了一个可与四大“山头”争诺奖的领域——复杂系统。因此，我们有理由如霍金所展望的那样，期待“二十一世纪是复杂系统的世纪”。 

 致 谢 

感谢和陈晋、苗兵、王振、符维成、施夏清的有益讨论。

【参考文献】

[1] G. Parisi and YongShi Wu, "Perturbation theory without gauge fixing." Scientia Sinica 24, no. 4 (1981): 483-496; 巴利希，吴詠时，“不用固定规范的微扰论.”中国科学 10, no. 12 (1980): 1172-1182.

[2] Edward N. Lorenz, "Deterministic nonperiodic flow." Journal of atmospheric sciences 20, no. 2 (1963): 130-141.

[3] Robert M. May, "Simple mathematical models with very complicated dynamics." Nature 261 (1976): 459.

[4] Tien-Yien Li and James A. Yorke, "Period three implies chaos." In The theory of chaotic attractors, pp. 77-84. Springer, New York, NY, 2004.

[5] Mitchell J. Feigenbaum, "Quantitative universality for a class of nonlinear transformations." Journal of statistical physics 19, no. 1 (1978): 25-52.

[6] James Hansen, Gary Russell, David Rind, Peter Stone, Andrew Lacis, Serge Lebedeff, Reto Ruedy, and L. Travis, "Efficient three-dimensional global models for climate studies: Models I and II." Monthly Weather Review 111, no. 4 (1983): 609-662.

[7] Syukuro Manabe, Joseph Smagorinsky, and Robert F. Strickler, "Simulated climatology of a general circulation model with a hydrologic cycle." Monthly Weather Review 93, no. 12 (1965): 769-798.

[8] Syukuro Manabe, and Richard T. Wetherald, "Thermal equilibrium of the atmosphere with a given distribution of relative humidity." Journal of the Atmospheric Sciences 24, no. 3 (1967): 241-259.

[9] 诺奖官网Popular science background,

https://www.nobelprize.org/uploads/2021/10/popular-physicsprize2021.pdf

[10] 诺奖官网Scientific Background，https://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf

[11] F. Fucito, F. Marchesoni, E. Marinari, G. Parisi, L. Peliti, S. Ruffo, and A. Vulpiani, "Approach to equilibrium in a chain of nonlinear oscillators." Journal de Physique 43, no. 5 (1982): 707-713.

[12] Giorgio Parisi, "On the approach to equilibrium of a Hamiltonian chain of anharmonic oscillators." EPL (Europhysics Letters) 40, no. 4 (1997): 357.

[13] Zhen Wang, Weicheng Fu, Yong Zhang, and Hong Zhao, "Wave-Turbulence Origin of the Instability of Anderson Localization against Many-Body Interactions." Physical Review Letters 124, no. 18 (2020): 186401.

作者简介

本文作者赵鸿、王矫、张勇、贺达海等教授来自厦门大学物理科学与技术学院复杂系统研究团队，这个团队在二十几年前就成立了复杂系统研究室，主要从事非线性动力学、非平衡统计物理、低维系统能量输运、量子动力学、量子经典对应、机器学习理论等方面的研究工作。

《复杂性思考：复杂性科学和计算模型（原书第2版）》

推荐语：复杂性科学使用计算来探索物理和社会科学。在本书中，你将使用图表、元胞自动机以及基于代理的模型来研究物理学、生物学和经济学。

更多精彩回顾

书讯 | 10月书讯（下） |  小长假我读这些新书

书讯 | 10月书讯（上） |  小长假我读这些新书

资讯 | 什么是图数据库？图数据库实践与创新浅析

书单 | 你们要的Java学习路线图来了

干货 | 数字化转型的1个目标，3大领域，6大因素和9个环节

收藏 | 两本书助你构建智能计算系统知识树

上新 | 【新书速递】从技术小白到开发大牛，这本实验教程带你手把手全栈开发！

赠书 | 【第77期】没有网络安全就没有国家安全

点击阅读全文购买