串、数组、广义表（详细）

串、数组、广义表

串

串的定义和特点

• 定义
  零个或多个任意字符组成的有限序列
  
  

• 有关术语

  • 子串：一个串中任意个连续字符串组成的子序列（含空串）
  • 真子串：指不包含自身的所有子串
  • 主串：包含子串的串相应地称为主串
  • 字符位置：字符在序列中的序号为该字符在串中的位置
  • 子串位置：子串第一个字符在主串中的位置
  • 空格串：有一个或多个空格组成的串
  • 串相等：当且仅当两个串的长度相等并且各个对应位置上的字符都相等
    
    

串的操作

• 串的存储
  串中元素逻辑关系与线性表相同，可以采用顺序和链式

串的顺序存储结构（数组实现）

#define MAXLIEN 255
typedef struct{
    char ch[MAXLIEN+1];//串数组
    int length;//串的长度
}SString;

串的链式存储–块链结构

#define CHUNKSIZE 80
typedef struct Chunk{
    char ch[CHUNKSIZE];
    struct Chunk *next;
}Chunk;
typedef struct{
    Chunk *head,*tail;
    int curlen;
}LString;

串的模式匹配

• 算法目的
  确定主串中所含子串（模式串）第一次出现的位置（定位）

• 算法应用

  • 搜索引擎、拼写检查、语言翻译、数据压缩

• 算法种类
  BF算法–穷举法
  KMP算法（速度快）

BF算法

• BF算法**
  也称为简单匹配算法–采用穷举法

  • 思路：从S的每一个字符开始依次与T的字符进行匹配

• 算法思路–Index(S,T,pos)
  将主串的第pos个字符和模式串的第一个字符比较

  • 若相等,继续逐个比较后续字符
  • 若不等,从主串的下一字符起,重新与模式串的第一个字符比较。
    直到主串的一个连续子串字符序列与模式串相等。返回值为S中与T匹配的子序列第一个字符的序号,即匹配成功。否则,匹配失败,返回值0

• 代码实现

int Index_BF(SString S,SString T){
  int i=1,j=1;
  while(i<S.length&&j<=T.length){
    if(S.ch[i]==T.ch[j]) ++i,++j;//匹配
    else i=i-j+2,j=1;//回溯
  }
  if(j>=T.length) return i-T.length;//匹配成功
  else return 0;//匹配不成功
}

• 算法时间复杂度
  主串长度n，子串长度m
  • 最好情况–O(m)
  • 最坏情况–O(n*m)
• 平均O($n^2$)
  
  

KMP算法

• 算法设计思想
  利用已经部分匹配的结果而加快模式串的滑动速度，且主串S的指针不必回溯，可提速到O(n+m)

• next数组的实现

• 代码实现

const int N=1e6+10;
int next[N];
void get_next(SString T,int &next[]){//next数组的实现
  int i=1,j=0;next[1]=0;
  while(i<T.length){
    if(j==0||T.ch[i]==T.ch[j]){
      ++i,++j;
      next[i]=j;
    }else{
      j=next[j];
    }
  }
}

int Index_BF(SString S,SString T,int pos){//模式匹配
  int i=1,j=1;
  i=pos;
  while(i<S.length&&j<=T.length){
    if(j==0||S.ch[i]==T.ch[j]) ++i,++j;//匹配
    else j=next[j];//回溯
  }
  if(j>=T.length) return i-T.length;//匹配成功
  else return 0;//匹配不成功
}

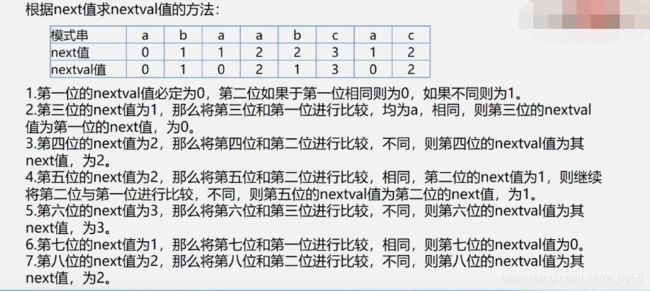
• nextval数组实现–next数组改进版

代码实现：

void get_nextval(SString T,int &nextval[]){
  int i=1,j=0;nextval[1]=0;
  while(i<T.length){
    if(j==0||T.ch[i]==T.ch[j]){
      ++i,++j;
      if(T.ch[i]!=T.ch[j])nextval[i]=j;
      else nextval[i]=nextval[j];
    }else{
      j=nextval[j];
    }
  }
}

数组

数组的定义和特点

• 定义：按一定格式排列起来，具有相同类型的数据元素的集合
  
  

• 一维数组：若线性表中的数据元素为非结构的简单元素则称为一维数组。

  • 一维数组的逻辑结构:线性结构。定长的线性表。
  • 声明格式:数据类型变量名称（长度）
    
    

• 二维数组：若一维数组中的数据元素又是一维数组结构,则称为二维数组
  
  

$$二维数组的逻辑结构=\{\begin{array}{ll}非线性结构：& 每一个数据元素既在一个行表中,又在一个列表中\\ 线性结构定长的线性表：& 该线性表的每个数据元素也是一个定长的线性表\end{array}$$

• 声明格式：数据类型 变量名称[行数][列数]
  
  

• 三维数组:若二维数组中的元素又是一个一维数组,则称作三维数组。
  
  

• n维数组:若n-1维数组中的元素又是一个一维数组结构则称作n维数组。
  
  

• 数组特点:结构固定一一定义后,维数和维界不再改变。
  
  

• 结论：线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展。

数组的顺序存储

• 一维数组
  每个元素的首地址计算方法：

$$LOC(i)=\{\begin{array}{ll}LOC(0)=a& i=0\\ LOC(i-1)+L=a+i\ast L& i>0\end{array}$$

• 二维数组
  有二维数组A[m][n]:
  以行序为主序：设数组开始存储位置LOC(0,0),存储每个元素需要L个存储单元
  数组元素a[i][j]的存储位置是：$LOC(i,j)=LOC(0,0)+(n\ast i+j)\ast L$

• 三维数组
  $a[m_1][m_2][m_3]$各维元素个数为$m_1,m_2,m_3$
  下标$i_1,i_2,i_3$的数组元素的存储位置：
  $LOC(i_1,i_2{i}_3)=a+i_1\ast m_2\ast m_3+i_2\ast m_3+i_3$–第$i_1$页总元素个数$+$第$i_1$页的前$i_2$行总元素$+$第$i_2$行前$i_3$列元素个数

特殊矩阵的压缩

• 特殊矩阵的压缩存储
  矩阵：一个由m×n个元素排成的m行n列的表
  矩阵的常规存储：将矩阵描述为一个二维数组
  矩阵的常规存储特点：1.可以对其元素进行随机存取。2.矩阵运算非常简单；存储的密度为1。
  不适宜常规存储的矩阵：值相同的元素很多且某种规律分布；零元素多。

• 什么是压缩存储
  若多个数据元素的值都相同，则只分配一个元素值得存储空间，且零元素不占存储空间。

• 什么样的矩阵能够压缩
  一些特殊矩阵，eg：对称矩阵、对角矩阵、三角矩阵、稀疏矩阵等。

• 什么叫稀疏矩阵
  矩阵中非零元素的个数较少（一般小于5%）

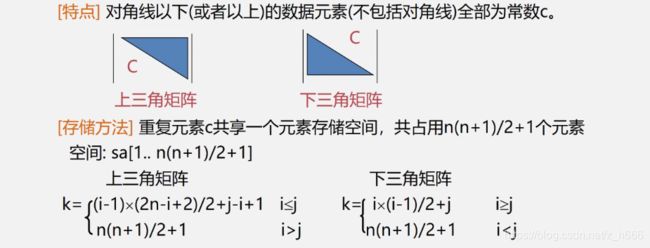
对称矩阵

三角矩阵

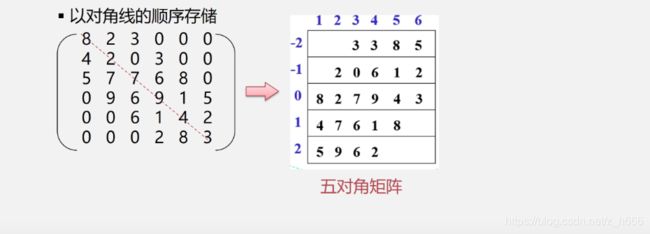
对角矩阵

对角矩阵存储：

稀疏矩阵

定义：稀疏矩阵:设在mxn的矩阵中有个非零元素。令$\delta =t/(mxn)$,当$\delta \le 0.05$时称为稀疏矩阵。

三元组法存储

• 三元组存储：$(i,j,a_{ij})$,行号，列号，数值

• 压缩存储原则:存各非零元的值、行列位置和矩阵的行列数。
  三元组的不同表示方法可决定稀疏矩阵不同的压缩存储方法。

• 三元组顺序表又称有序的双下标法。

• 三元组顺序表的优点:非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。

• 三元组顺序表的缺点:不能随机存取若按行号存取某一行中的非零元,则需从头开始进行查找。

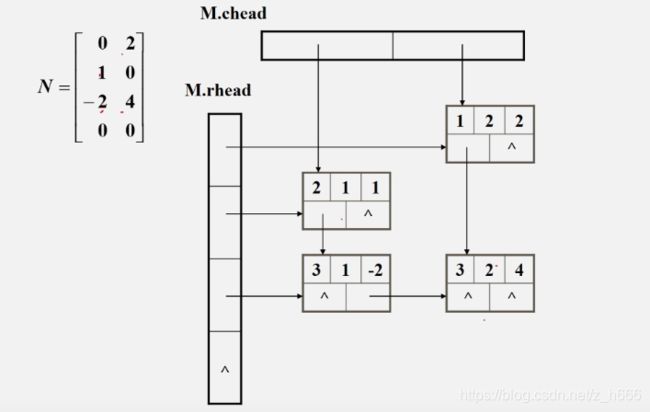
十字链表

• 优点:它能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素,实现矩阵的各种运算。
• 在十字链表中,矩阵的每一个非零元素用一个结点表示
  该结点除了(row,col, value))以外,还要有两个域:
  • right::用于链接同一行中的下一个非零元素
  • down:用以链接同一列中的下一个非零元素。
• 十字链表中结点的结构示意图:

value	row	col
down	right

例如：

广义表

广义表(又称列表 Lists)是$n\ge 0$个元素$a_0,a_1,\cdot \cdot \cdot ,a_{n-1}$的有限序列,其中每一个$a_i$或者是原子,或者是一个广义表。

• 相关概念
  • 广义表通常记作:$LS=(a_1,a_2,...,a_n)$
    其中:$LS$为表名,$n$为表的长度,每一个$a_i$为表的元素。
  • 习惯上,一般用大写字母表示广义表,小写字母表示原子。
  • 表头:若$LS$非空$(n\ge 1)$,则其第一个元素$a_1$就是表头。
    记作:$head(LS)=a_1$。注:表头可以是原子,也可以是子表。
  • 表尾:除表头之外的其它元素组成的表。
    记作:$tail(LS)=(a_2,...,a_n)$
    注:表尾不是最后一个元素,而是一个子表。

例子：

• 广义表的性质
  (1)广义表中的数据元素有相对次序;一个直接前驱和一个直接后继;
  
  (2)广义表的长度定义为最外层所包含元素的个数;
  
  如:$C=(a,(b,c)$是长度为2的广义表。
  
  (3)广义表的深度定义为该广义表展开后所含括号的重数;
  $A=(b,c)$的深度为1,$B=(A,d)$的深度为2,$C=(f,B,h)$的深度为3。
  注意:“原子”的深度为0;“空表”的深度为1
  
  (4)广义表可以为其他广义表共享;如:广义表B就共享表A在B中不必列出A的值,而是通过名称来引用,$B=(A)$。
  
  (5)广义表可以是一个归的表。如:$F=(a,F)=(a,(a(a(a,...))))$
  注意:递归表的深度是无穷值,长度是有限值
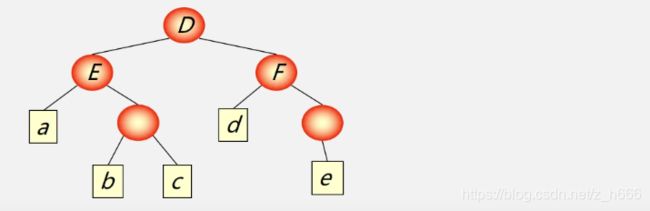
  (6)广义表是多层次结构,广义表的元素可以是单元素,也可以是子表,而子表的元素还可以是子表,…可以用图形象地表示。
  例:$D=(E,F)$ 其中:$E=(a,(b,c))$ $F=(d,(e))$

• 广义表与线性表的区别
  
  广义表可以看成是线性表的推广,线性表是义表的特例。
  
  广义表的结构相当灵活,在某种前提下,它以兼容线性表、数组、树和有向图等各种常用的数据结构
  
  当二维数组的每行(或每列)作为子表处理时,二维数组即为一个广义表。
  
  另外,树和有向图也可以用广义表来表示。
  
  由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点,而且可有效地利用存储空间,因此在算机的许多应用领域都有成功使用广义表的实例。
  

• 广义表的基本运算
  (1)求表头 GetHead((L):非空广义表的第一个元素,可以是一个元素，也可以是一个子表。
  
  (2)求表尾 GetTail((L):非空广义表除去表头素以外其它元素所构成的表。表尾一定是一个表。
  
  例:

  $D=(E,F)=(a,(b,c),F)$
  
  $GetHead(D)=E$   $GetTail(D)=(F)$
  
  $GetHead(E)=a$   $GetTail(E)=((b,c))$
  
  $GetHead(((b,c)))=(b,c)$ $GetTail(((b,c)))=()$
  
  $GetHead((b,c))=b$ $GetTail((b,c))=(c)$
  
  $GetHead((c))=c$     $GetTail((c))=()$
  

案例分析

案例4.1 病毒感染检测

• 串的模式匹配
  • BF算法
  • KMP算法

因为病毒是环状的，解决办法–滑动窗口

• 案例实现：