红黑树之概述
红黑树
R-B Tree,全称是 Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL 或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
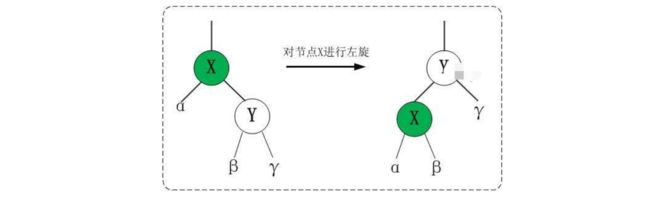
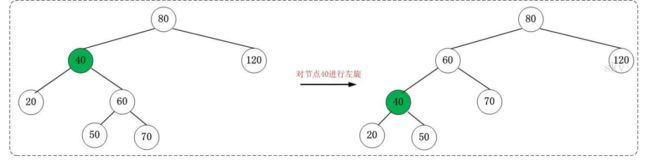
左旋
对 x 进行左旋,意味着,将“x 的右孩子”设为“x 的父亲节点”;即,将 x 变成了一个左节点(x成了为 z 的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
LEFT-ROTATE(T, x)
y ← right[x] // 前提:这里假设 x 的右孩子为 y。下面开始正式操作
right[x] ← left[y] // 将 “y 的左孩子” 设为 “x 的右孩子”,即 将β设为 x 的右孩子
p[left[y]] ← x // 将 “x” 设为 “y 的左孩子的父亲”,即 将β的父亲设为 x
p[y] ← p[x] // 将 “x 的父亲” 设为 “y 的父亲”
if p[x] = nil[T]
then root[T] ← y // 情况 1:如果 “x 的父亲” 是空节点,则将 y 设为根节点
else if x = left[p[x]]
then left[p[x]] ← y // 情况 2:如果 x 是它父节点的左孩子,则将 y 设为“x 的父节点
的左孩子”
else right[p[x]] ← y // 情况 3:(x 是它父节点的右孩子) 将 y 设为“x 的父节点的右孩
子”
left[y] ← x // 将 “x” 设为 “y 的左孩子”
p[x] ← y // 将 “x 的父节点” 设为 “y”
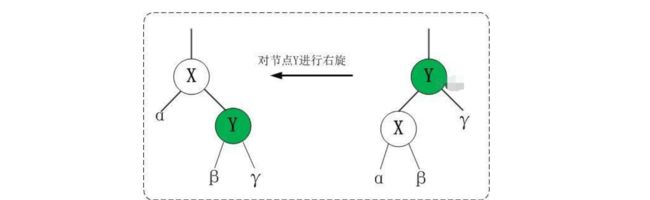
右旋
对 x 进行右旋,意味着,将“x 的左孩子”设为“x 的父亲节点”;即,将 x 变成了一个右节点(x成了为 y 的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
RIGHT-ROTATE(T, y)
x ← left[y] // 前提:这里假设 y 的左孩子为 x。下面开始正式操作
left[y] ← right[x] // 将 “x 的右孩子” 设为 “y 的左孩子”,即 将β设为 y 的左孩子
p[right[x]] ← y // 将 “y” 设为 “x 的右孩子的父亲”,即 将β的父亲设为 y
p[x] ← p[y] // 将 “y 的父亲” 设为 “x 的父亲”
if p[y] = nil[T]
then root[T] ← x // 情况 1:如果 “y 的父亲” 是空节点,则将 x 设为根节点
else if y = right[p[y]]
then right[p[y]] ← x // 情况 2:如果 y 是它父节点的右孩子,则将 x 设为“y 的父节
点的左孩子”
else left[p[y]] ← x // 情况 3:(y 是它父节点的左孩子) 将 x 设为“y 的父节点的左孩
子”
right[x] ← y // 将 “y” 设为 “x 的右孩子”
p[y] ← x // 将 “y 的父节点” 设为 “x”
添加
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
第二步:将插入的节点着色为"红色"。
根据被插入节点的父节点的情况,可以将"当节点 z 被着色为红色节点,并插入二叉树"划分为三
种情况来处理。
① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。
② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。
③ 情况说明:被插入的节点的父节点是红色。这种情况下,被插入节点是一定存在非空祖父节点的;进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为 3种情况(Case)。
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
删除
第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分 3 种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就 OK 了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
选择重着色 3 种情况。
① 情况说明:x 是“红+黑”节点。
处理方法:直接把 x 设为黑色,结束。此时红黑树性质全部恢复。
② 情况说明:x 是“黑+黑”节点,且 x 是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。
③ 情况说明:x 是“黑+黑”节点,且 x 不是根。
处理方法:这种情况又可以划分为 4 种子情况。这 4 种子情况如下表所示: